基于突变理论的风电场静态电压稳定分析方法

葛江北， 张亚鹏， 阎国增， 李国满， 王振明， 卞秀杰， 王天宇

(国家电网公司交流建设分公司， 北京 100052)

基于突变理论的风电场静态电压稳定分析方法

葛江北， 张亚鹏， 阎国增， 李国满， 王振明， 卞秀杰， 王天宇

(国家电网公司交流建设分公司， 北京 100052)

目前，对于风电场静态电压稳定的分析，多是将传统的静态电压稳定分析方法沿用至此。这些方法计算复杂，因此有必要采用新的方法对风电场的静态电压稳定进行研究。本文着重采用突变理论，基于单风场送出系统，从外特性的分析方式建立了其静态电压稳定模型，并对其应用进行展望，旨在提供一种新的风电场静态电压稳定分析方法。

风电场； 静态电压稳定； 突变理论； 外特性

1 引言

目前，风力发电技术在世界范围内得到了迅猛发展[1-3]，尤其是我国，拟建立8个千万千瓦级别的风电基地。风力发电与传统发电技术有较大不同，风电机组可以实现异步运行，不再有传统意义上的功角稳定，其稳定更多的表现为电压稳定和频率稳定，尤其是电压稳定，成为影响风电场及所联电网安全稳定运行的重要因素[4]。2012年5月14日，在无任何系统故障的情况下,我国张北沽源地区发生了大面积的风电机组连锁脱网事故，凸显了风电场的静态电压稳定问题[5]。因此，研究风电场的静态电压稳定具有重要的理论和实际意义。

目前，对风电场的静态电压稳定已有一定的研究，多是将传统的静态电压稳定分析方法沿用至风电场。文献[6]考虑了风电的随机性和间隙性，基于常规连续潮流法，考虑了风机脱网对系统静态电压稳定的影响，对风电场的静态电压稳定进行分析；文献[7]采用PV曲线方法，综合有功功率裕度和电压-有功灵敏度指标，分析了风电接入后对地区电压稳定性的影响；文献[8]以3节点电力系统为例，采用分岔理论，研究了含双馈风力发电机组的电力系统电压失稳的机理；文献[9]同样采用分岔理论，对含风电的电力系统电压稳定性进行了分析；文献[10]以特征结构分析法为理论基础，对包含风电场的电力系统的静态电压稳定问题进行了研究。总体来讲，目前的这些研究多侧重于风电接入下静态电压失稳机理的研究，往往基于理论推导的方式建立模型，计算过程非常复杂，同时其对于风电场静态电压失稳的机理解释也并不一致。因此，有必要采用新的方法对风电场的静态电压稳定进行研究。

突变理论提供了一种基于外特性的经验建模方法，简单迅速。基于此，本文将探索采用突变理论对风电场的静态电压稳定进行研究，并对突变理论在风电场静态电压稳定中的应用进行展望，旨在对突变理论在风电场静态电压稳定分析中的应用进行初步探索。

2 突变理论及其应用

2.1 突变理论

自然界中存在很多有趣的现象，如桥梁的突然倒塌、细胞的分裂等，这些现象都涉及到不连续性。传统的微积分学在研究这些不连续现象时出现了困难，而突变理论可以对这种现象进行很好的描述。它由法国著名数学家Thom于20世纪60年代创立，之后则由Zeeman等人发展[11,12]，目前已在生物学[13]、社会科学[14]、岩土[15]、水利[16]等方面得到广泛应用。

突变理论的关键组成主要包括势函数、平衡曲面、奇点集和分歧点集等。若系统的动力学能够由一个光滑的势函数导出，其势函数为V(x)：X×C→R，其中x∈X为n维空间，表示状态变量；C为r维空间，表示控制变量。平衡曲面M为Rn×Rr空间的子集，由DV(x)=0定义，其中D为V对x的求导。奇点集S为由V的全部退化临界点组成的M的一个子集，满足D2V(x)=0。将S投影到控制空间C中，即可得到分歧点集B，它是C中所有使V的形状发生突变的点的集合。

突变理论表明，可能出现性质不同的连续构造的数目不取决于状态变量的数目(这可能很大)，往往取决于控制变量的数目(这一般比较小)。表1给出了7种基本突变名称及其势函数形式[11,12,17]，其中，x、y代表状态变量，v、μ、ω、t、w、υ代表控制变量。

表1 基本突变及其势函数Tab.1 Elementary catastrophe models and their potential functions

需要说明的是，表1中的势函数均为正则形式。所谓正则形式，是势函数的最为简化的形式。突变理论的势函数本质是基于状态变量的泰勒级数展开而截断了不必要的高阶项，它总可以通过微分同胚变换得到其最为简化的形式，即正则形式[11,18]。而对于单状态变量的突变模型，实际上只需用到线性变换即可[11,17]。

2.2 突变理论的应用

突变理论提供了一种经验建模方式，即在不知道系统势函数、平衡曲面或分歧点集数学描述的情况下，可根据系统外部性态建立其突变模型，最为常用的方法即为数据拟合。此时需要依据突变指征判定所研究系统是否适用于突变模型。

2.3 折叠突变

以本文所要用到的折叠突变为例[11]，基于势函数(见表1)，可得其平衡曲面M方程为：

DV(x)=3x2+v=0

(1)

式中，x为状态变量；v为控制变量。

奇点集S满足方程：

D2V(x)=6x=0

(2)

将式(1)和式(2)联立，可得其分歧点集B如式(3)所示：

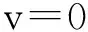
(3)

折叠突变的平衡曲面及分歧点集如图1所示。图1中，当控制变量v<0时，系统相点位于图1曲线部分，是一个连续的过程；而当v=0时，系统达到分歧点集，此时微小的扰动即会引起系统发生突跳，系统无法长期停留于此；一旦v>0，意味着系统突跳进入另外一个状态，从数学上来讲即无实数解，从而表现出不连续性和突跳。

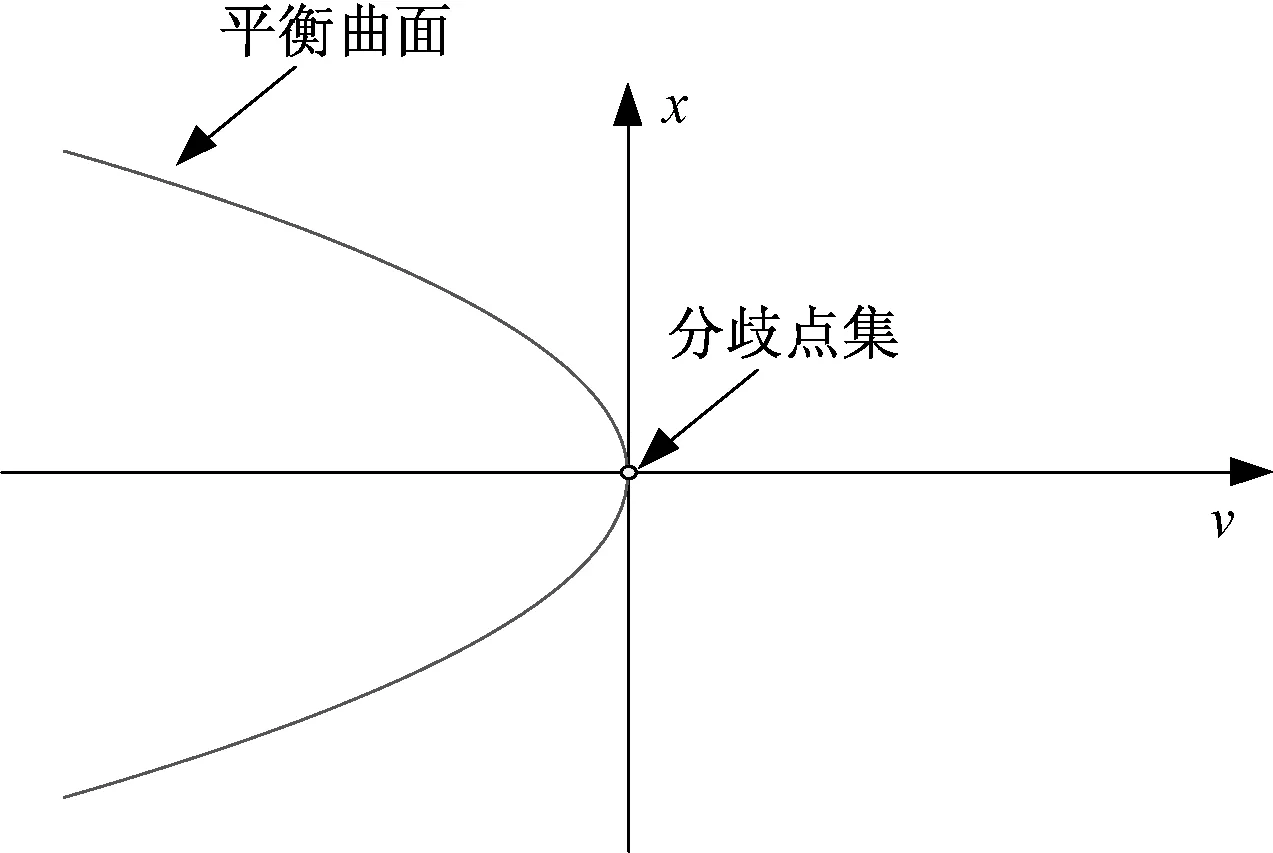
图1 折叠突变模型示意图Fig.1 Schematic diagram of fold catastrophe model

3 突变理论在风电场静态电压稳定中的应用

目前，突变理论在风电场电压稳定分析中的应用很少，尚未见到相关的文献。本文将着重针对单风场送出系统，采用突变理论建立风电场的静态电压突变模型。

3.1 突变指征

突变理论适用于表现出明显突变指征的系统。所谓突变指征主要是指失稳原型系统的一些特征。最易观察的突变指征包括多模态、突跳、不可达、发散等[11,17,18]。多模态指系统可能出现两个或多个不同的状态；突跳是最常观察到也最易使人想到可以应用突变理论的指征，系统平衡位置从消失的极小或者状态不稳定之处跨越到全局极小或一个局部极小状态时，其位势在短暂的时间内将有一个很大的改变；不可达是指系统无法长期处于系统的不稳定平衡点；发散是指对控制参数路径摄动的不稳定性，即通常情况下，对控制参数数值的一个微小摄动只会引起状态变量初值和终值的微小变化，但在退化临界点附近，控制参数初值的微小变化却可能导致状态变量终值发生很大改变。

3.2 风电场的静态电压变化过程分析

对于风电场，稳定状态下风场电压会随风场出力缓慢变化，这是一个准静态的过程，而当风场出力较大，达到临界点时，会造成系统电压的突然崩溃，这体现了多模态和突跳的特点；实际上，该临界点即为系统稳定的边缘，系统无法长期停留于此，风场出力微小的变化即可引起风场电压的突然崩溃，从而体现出不可达和发散的特点。

可见，风电场静态电压突变过程表现出明显的突变指征，显示出运用突变理论研究风电场群电压稳定的可行性。

3.3 模型的建立

突变理论的一个显著优点是针对具有突变指征的系统，即使在机理不明的情况下，仍可采用经验方式建立其模型。风电场的静态电压变化过程已显示出其具有明显的突变指征。

此时，可依据独立控制变量和状态变量选择合适的突变模型，进行数据拟合或定性拟合。考虑单风电场送出系统中最为常用的功率因数为1的运行方式，此时风电场PCC母线电压受风电场出力控制，则风电场出力P为独立控制变量，PCC母线电压U1为状态变量(在突变理论中，状态变量表示被观察的变量)，即1个状态变量和1个独立控制变量，能够且只能够选择折叠突变模型。

需要说明的是，突变理论的势函数一般是基于状态变量的泰勒级数展开而截断了不必要的高阶项(突变理论的一项成就在于它为截断提供了一个严格的证明，其证明很复杂，不再给出)，并经微分同胚变化得到最简化形式(即正则形式，表1中的势函数均为正则形式)。对于折叠突变，实际应用中只需通过线性变换即可。因此，所选择的控制变量和状态变量与正则形式对应的变量可相差一个系数和一个常数[11,17]。正则形式下，折叠突变模型的平衡曲面方程如式(1)所示。则，考虑适当的线性变换，其平衡曲面方程M可表示为：

(4)

式中，k、a、b为待求系数。

由于稳态运行点均应在平衡曲面上，因此采集正常运行时P不同出力下风电场的电压U1，将其代入式(4)，通过数据拟合可得到相应的未知量，从而建立其对应的突变模型。之后即可进行风电场电压的分析。

3.4 模型验证

(1)模型1

在DIgSILENT/PowerFactory仿真软件上搭建单风电场送出系统，如图2所示。其中，风电场为200台风机并列，T1为35kV/0.69kV，容量444.4MV·A，uk%=0，连接方式为YNyn0；T2为110kV/35kV，容量为450MV·A，uk=11%，连接方式为YNyn0；T3为220kV/110kV，容量为500MV·A，uk=11%，连接方式为YNyn0；L1型号为LGJ-240，长度为10km； L2型号为LGJ-400，长度为100km。

图2 单风场送出系统(模型1)Fig.2 Single wind farm sending-out system (model 1)

由3.3节分析可知，经验方式下其对应的平衡曲面方程如式(4)所示，则采集一定数量的风电场出力-风电场电压数据，当采集数量超过未知数数量时，即构成超定非线性方程组。通过数据拟合求得未知数，从而得到对应的突变模型。采集样本数据如表2所示。

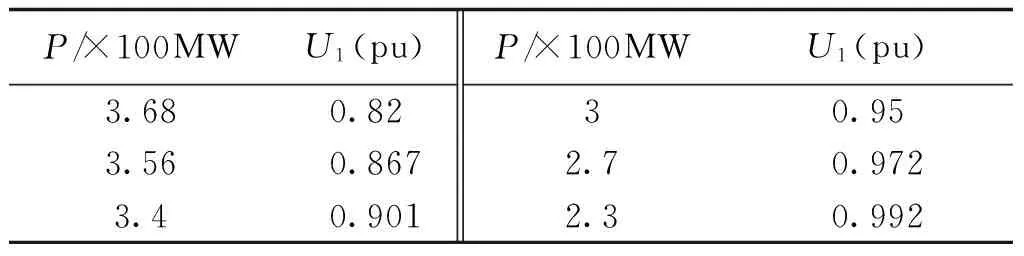
表2 采集数据样本(模型1)Tab.2 Collected data samples (model 1)

经拟合，可得其平衡曲面方程为：

V′(U1)=51.3247(U1-0.8321)2+P-3.6636

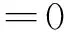
(5)

则，可得：

(6)

以式(6)所得到理论值与实际的仿真值进行对比，如图3所示。可以看出，理论值与仿真值有较好的一致性，尤其是在靠近临界点处的运行点，二者非常接近。

实际上，由于这种方法是采集数据进行拟合计算，因此，其对于风电送出后接入小系统的情况同样适用且可以保持其精度。

(2)模型2

将图2中的无穷大系统改为一个220kV的小系统，如图4所示。其中，L3、L4、L5型号均为LGJ-400，长度分别为52km、47km、107km。Load1、Load2、Load3大小分别为1.67-j0.25pu、0.63+j0.15pu、0.89+j0.2pu(1pu=100MV·A)。采用同样的方法，采集数据如表3所示。

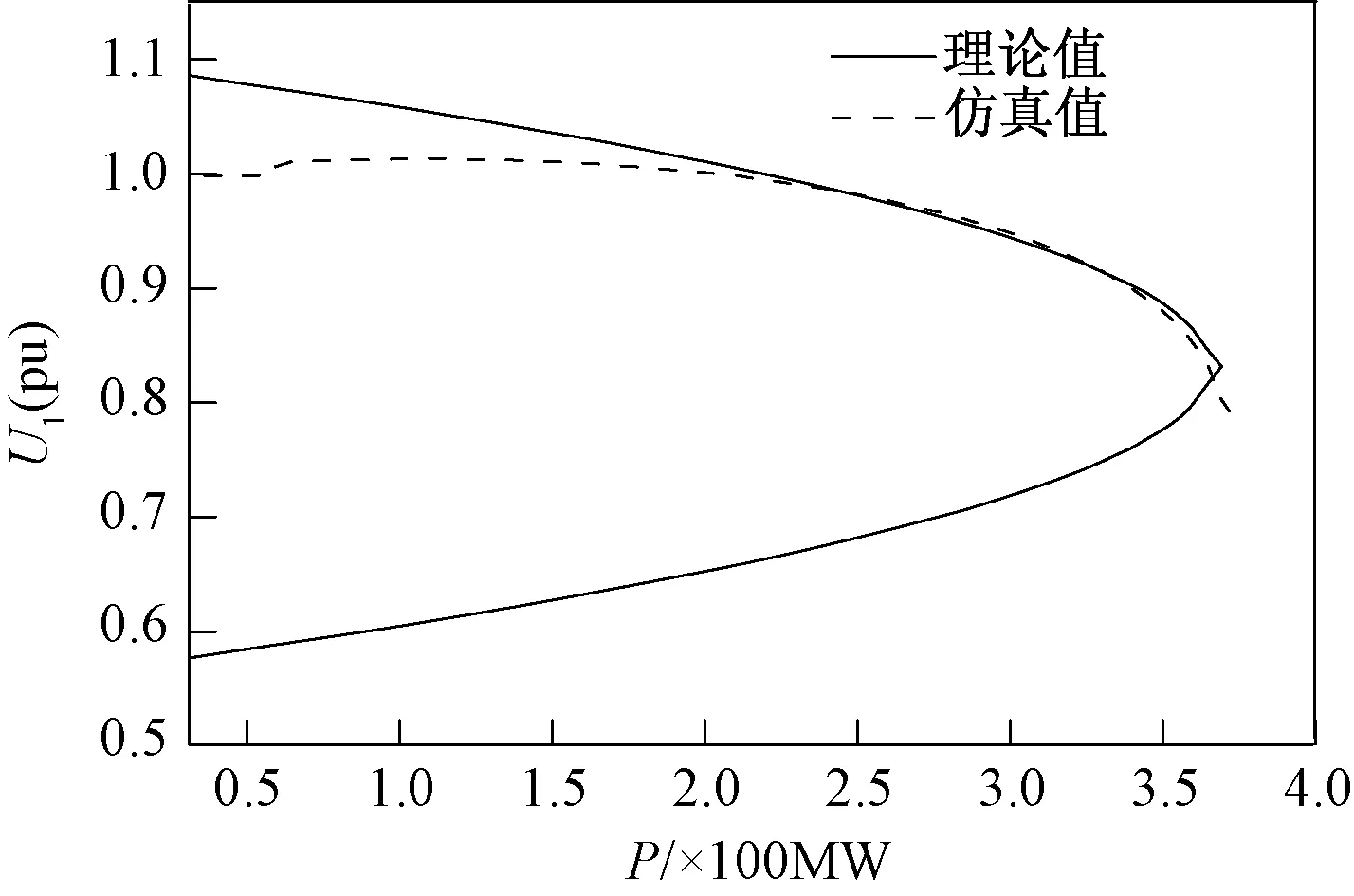
图3 理论值和仿真值的对比(模型1)Fig.3 Comparison of theoretical values and simulation values (model 1)

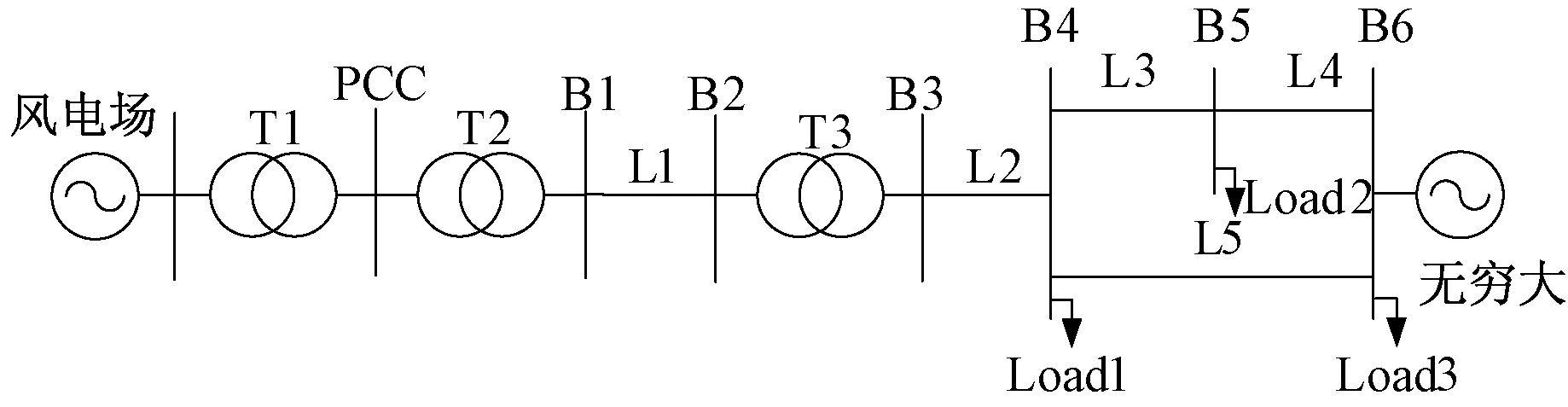
图4 单风场送出系统(模型2)Fig.4 Single wind farm sending-out system (model 2)

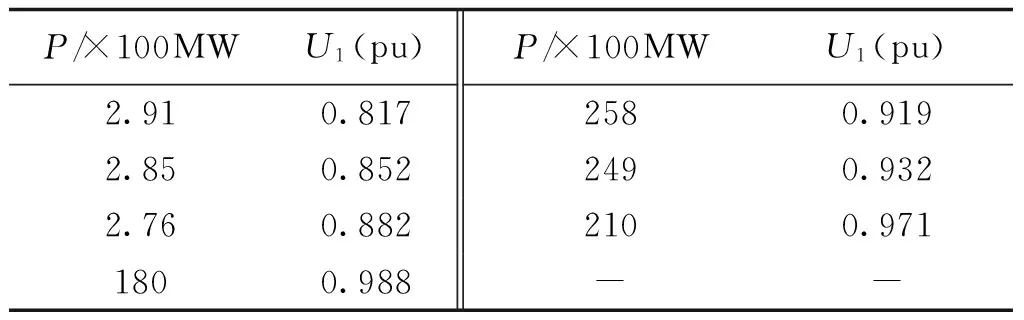
表3 采集数据样本(模型2)Tab.3 Collected data samples (model 2)

经拟合，可得其平衡曲面方程为：

V′(U1)=43.6111(U1-0.8326)2+P-2.8957

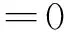
(7)

则，可得：

(8)

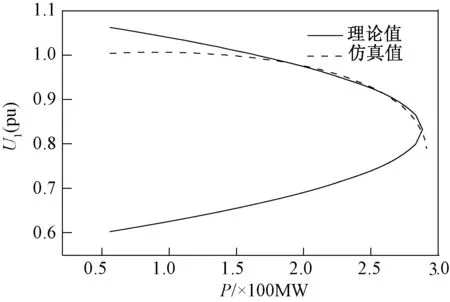
图5 理论值和仿真值的对比(模型2)Fig.5 Comparison of theoretical values and simulation values (model 2)

其理论值与仿真值的对比如图5所示。可以看出，同样的风电场送出系统，其直接接入无穷大系统和接入一个小系统时，二者的仿真曲线具有较大的差异。但无论何种情况，通过拟合得到的理论值与仿真值仍然具有较好的一致性。

4 突变模型的推广

传统的静态电压稳定分析方法在应用时，采用的均为基于模型推导的方法，由于电力系统的高阶数和强非线性，这种方法往往无法直接通过非线性方程求解，而需要将非线性方程组线性化后迭代求解。这种情况下，一方面计算极其复杂，另一方面也难以应付多参数同时变化的情况。因此，目前传统的静态电压稳定分析方法在进行风电场电压稳定的分析时也往往将风电场等值为1台风机，研究风机出力变化时风电场的电压变化过程。对于多风电场出力同时随机波动的情况则缺乏有力的分析工具。

突变理论则提供一种基于外特性的经验建模方式。由于经验方法不依赖具体的模型，而只依赖所采用的数学函数形式和所采集的数据，因此，其方法简单有效。目前突变理论已可以给出控制参数不大于5情况下其势函数形式。作者已针对多风电场，采用突变理论的经验方式进行了研究，并在双风电场送出系统中验证了其有效性。图6为双风电场情况下系统的分歧点集与仿真临界点的对比图。可以看出，二者有较好的一致性。对于多风电场的情况另具文描述，此处不再详细展开。

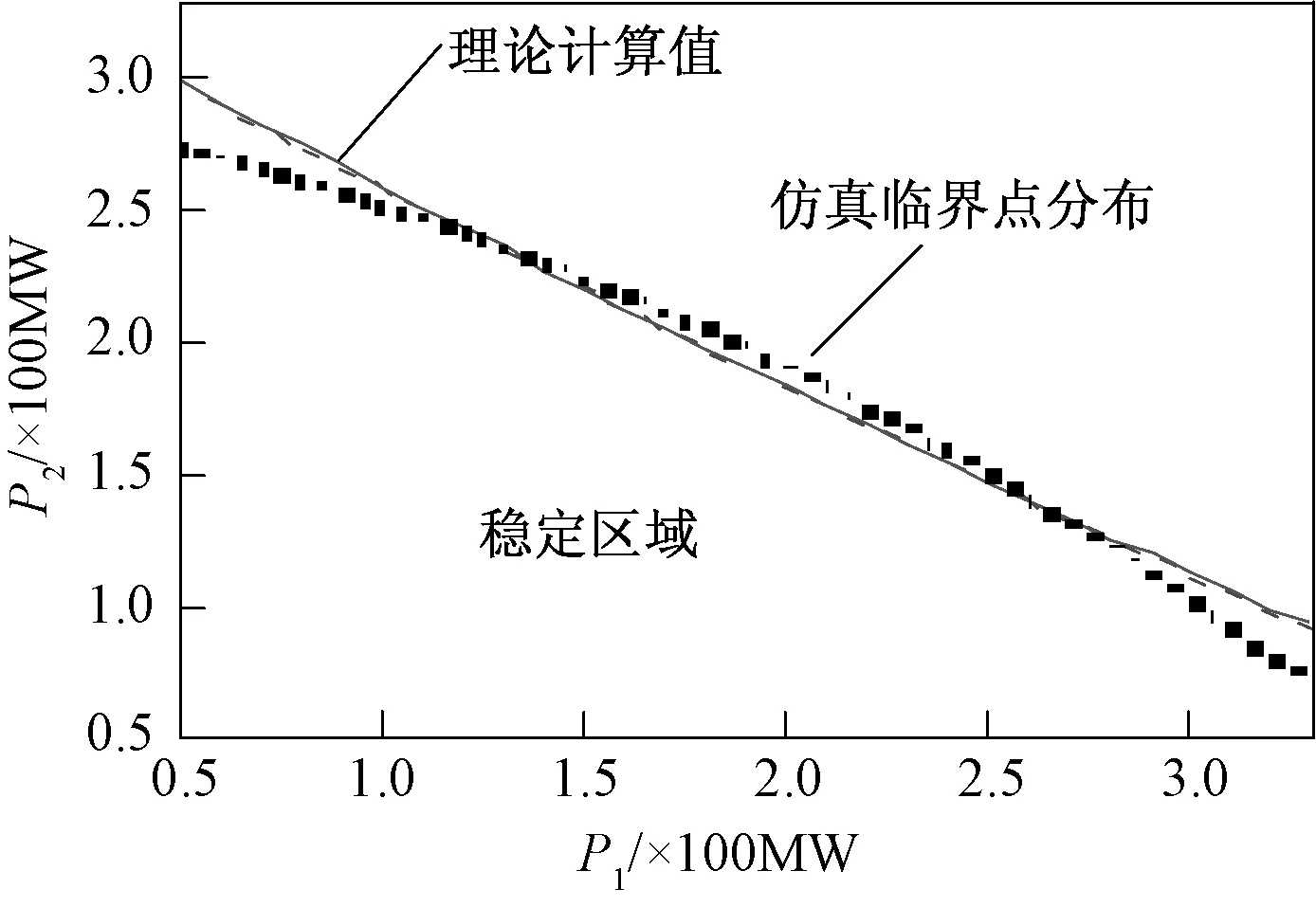
图6 稳定边界比对Fig.6 Comparison of stability margin

5 结论

本文基于突变理论，通过外特性的建模方法进行了风电场静态电压稳定模型的建立，并对其在多风电场中的应用进行讨论，为风电场静态电压稳定的分析提供方法支持。

本文考虑了风电场功率因数为1情况下的静态电压分析，实际上随着技术的发展，风电场将被要求也有能力提供一定的无功电压支持，这些情况将在后续工作中进行进一步的研究。

[1] 曾令全，王立娟(Zeng Lingquan，Wang Lijuan)．基于概率的含大规模风电场的多目标输电网规划(Multi-objective transmission planning associated with large scale wind farms based on probability)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2013，32(4)：11-14.

[2] 李鹏波，罗荣钧，牟春晓，等(Li Pengbo，Luo Rongjun，Mou Chunxiao，et al．)．基于机组组合的风电消纳能力研究(Digestion of wind power based on unit commitment)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2015，34(8)：25-30.

[3] 梁智敏，高亮(Liang Zhimin，Gao Liang)．提高双馈风电机组故障穿越能力的组合技术方案研究(Research on combined technical scheme of fault ride-through of DFIG wind turbine)[J]．电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2016，35(7)：62-68.

[4] 鲍海波，韦化(Bao Haibo，Wei Hua)．考虑风电的电压稳定概率评估的随机响应面法(A stochastic response surface method for probabilistic evaluation of the voltage stability considering wind power)[J]．中国电机工程学报(Proceedings of the CSEE), 2012，32(13)：77-85.

[5] 许晓菲，牟涛，贾琳，等(Xu Xiaofei，Mu Tao，Jia Lin，et al．)．大规模风电汇集系统静态电压稳定实用判据与控制(Practical criteria of static voltage stability in power systems with high wind penetration)[J]．电力系统自动化(Automation of Electric Power Systems), 2014，38(9)：15-19.

[6] 熊传平，张晓华，孟远景，等(Xiong Chuanping，Zhang Xiaohua，Meng Yuanjing，et al．)．考虑大规模风电接入的系统静态电压稳定性分析(Analysis on static voltage stability of system with large-scale wind power integration)[J]．电力系统保护与控制(Power System Protection and Control), 2012，40(21)：132-137.

[7] 许晓艳，马烁，黄越辉，等(Xu Xiaoyan，Ma Shuo，Huang Yuehui，et al．)．大规模风电接入对电网静态电压稳定性影响机理研究(Mechanical study on influence of large scale wind power on static voltage stability)[J]．中国电力(Electric Power), 2015，48(3)：139-143.

[8] 杨黎晖，马西奎(Yang Lihui，Ma Xikui)．基于分岔理论的含双馈风电机组的电力系统电压稳定性分析(Analysis on voltage stability of power system with doubly fed induction generator wind turbine based on bifurcation theory)[J]．电工技术学报(Transactions of China Electrotechnical Society), 2012，27(9)：1-8.

[9] 马幼捷，张继东，周雪松，等(Ma Youjie，Zhang Jidong，Zhou Xuesong，et al．)．含风电电力系统电压稳定问题的分岔(Bifurcation of steady state voltage stability with wind power system)[J]．电力系统及其自动化学报(Proceedings of the CSU-EPSA), 2008，20(5)：117-123.

[10] 马幼捷，张继东，周雪松，等(Ma Youjie，Zhang Jidong，Zhou Xuesong，et al．)．特征结构分析法对风电系统静态电压稳定的研究(Study on steady state voltage stability of power systems including wind farms based on eigen-structure analysis)[J]．中国电力(Electric Power), 2008，14(3)：87-92.

[11] 桑博德(P T Saunders)．突变理论入门(An introduction to catastrophe theory)[M]．凌复华，译(Lin Fuhua，Translated)．上海：上海交通大学出版社(Shanghai：Shanghai Jiao Tong University Press)，1983. 5-17．

[12] E C Zeeman. Catastrophe theory[J]. Scientific American, 1976, 236(4): 65-83.

[13] A E R Woodcock. Landscapes of change: Catastrophe theory and biological processes[J]. Behavioral Science, 1978, 23(4):390-401.

[14] 戢晓峰，梁斐雯，陈方(Ji Xiaofeng，Liang Feiwen，Chen Fang)．基于突变理论的过饱和旅游应急疏散效率评价方法(Evaluation method of emergency evacuation efficiency for hype-congestion tourism flow based on catastrophe theory)[J]．经济地理(Economic Geography), 2013，33(5)：168-173.

[15] 周小平，钱七虎，张永兴，等(Zhou Xiaoping，Qian Qihu，Zhang Yongxing，et al.)．基于突变理论的滑坡时间预测模型(Time prediction model of landslides based on catastrophe theory)[J]．工程力学(Engineering Mechanics), 2011，28(2)：165-174.

[16] 李绍飞，孙书洪，王向余(Li Shaofei，Sun Shuhong，Wang Xiangyu)．突变理论在海河流域地下水环境风险评价中的应用(Application of catastrophe theory to risk assessment of groundwater environment for river basin)[J]．水利学报(Journal of Hydraulic Engineering), 2007，38(11)：1312-1317.

[17] 全玉生，谌军，李巍，等(Quan Yusheng，Chen Jun，Li Wei，et al．)．基于突变理论的油浸式变压器过热性故障预测方法(Methodology of forecasting the oil-immersed transformer over-hot fault tendency based on catastrophe theory)[J]．中国电机工程学报(Proceedings of the CSEE), 2011，31(18)：100-106.

[18] 吉尔莫雷(R Gilmore)．科学与工程中的基本突变理论(Catastrophe theory for scientists and engineers)[M]．湛垦华，刘秉钧，译(Zhan Kenhua, Liu Bingjun, Translated)．西安：西安交通大学出版社(Xi’an：Xi’an Jiaotong University Press)，1988. 154-176．

Wind farm static voltage stability analysis method based on catastrophe theory

GE Jiang-bei, ZHANG Ya-peng, YAN Guo-zeng, LI Guo-man, WANG Zhen-ming,BIAN Xiu-jie, WANG Tian-yu

(State Grid AC Engineering Construction Company，Beijing 100052, China)

Currently, in the study of static voltage stability of wind farm, traditional static voltage stability analysis methods are often used. These methods are very complex. Therefore, it is necessary to adopt a new method to study wind farm static voltage stability. So, based on single wind farm sending-out system, catastrophe theory is focused. The static voltage stability model is established through external characteristics method. Application of catastrophe theory is prospected, aiming to provide a new method for the wind farm static voltage stability analysis.

wind farm; static voltage stability; catastrophe theory; external characteristics

2016-05-05

葛江北(1987-)， 男， 河南籍， 工程师， 博士， 研究方向为新能源接入电力系统分析、 输变电工程管理； 张亚鹏(1973-)， 男， 河南籍， 高级工程师， 研究方向为输变电工程管理。

TM74

A

1003-3076(2016)12-0020-06