基于二阶滑模观测器的感应电机转子磁链观测

徐 静， 杨淑英， 郭磊磊， 张 兴

(合肥工业大学电气与自动化工程学院， 安徽 合肥 230009)

基于二阶滑模观测器的感应电机转子磁链观测

徐 静， 杨淑英， 郭磊磊， 张 兴

(合肥工业大学电气与自动化工程学院， 安徽 合肥 230009)

实现矢量控制的基础是准确获得转速和转子磁链信息，本文提出了一种基于二阶滑模观测器的转子磁链观测方法。将构造的滑模观测器作为模型参考自适应系统(MRAS)的参考模型，将磁链的电流模型改造为该中间变量的可调模型，且其可调量为转速变量，进而构造出MRAS，实现对转速的观测。在此基础上，完成转子磁链的计算，并得到转子磁链角度，实现基于直接磁场定向的感应电机矢量控制。中间量的构造有效避免了传统MRAS中的纯积分问题，便于算法的实施；二阶滑模观测器有效地削弱了一阶滑模观测器存在的抖振扰动，并且参数具有较强的鲁棒性。仿真结果表明该转子磁链观测器具有较高的观测精度，且对外部扰动和转子电阻变化具有较强的鲁棒性，提高了系统的动稳态性能。

感应电机； 二阶滑模； MRAS； 磁链观测； 无传感器控制

1 引言

感应电机的低成本和免维护等特点使其在工业生产中得到了广泛应用[1]。矢量控制技术的发展，使其调速性能得到了显著改善。转速及矢量定向是直接影响调速性能的两个重要因素[2]。转速信息虽然可通过机械速度传感器获得，但会增加控制系统的成本和机械安装的复杂性，降低系统的可靠性[3]。而无速度传感器技术可有效避免上述弊端，因此其成为近年来国内外学者研究的热点。转子磁链信息可以通过直接测量获得，但直接测量法较难在实际系统中实现[4]，因此常采用间接观测的方法来获取转子磁链[5]。即根据电机的数学模型构造出观测器实现对转子磁链的观测。

目前，常见的观测方案有：扩展的卡尔曼滤波器(EKF)[6]、全阶状态观测器[7]、模型参考自适应系统(MRAS)[8]以及滑模观测器[9，10]等。基于扩展的卡尔曼滤波器(EKF)法可以在较宽的转速范围内稳定工作，但计算量较大，且易受噪声的影响；全阶状态观测器对参数具有较强的依赖性，且反馈增益矩阵的设计较复杂；MRAS的算法原理较简单，但对参数变化较为敏感；而滑模观测器算法因实现简单，具有较强的抗干扰能力以及鲁棒性，而备受国内外学者的关注。然而基于一阶滑模理论设计的观测器受困于抖振等问题[9，10]，限制了其应用，而采用高阶滑模观测器[4]不仅可以有效地削弱抖振而且具有较强的参数鲁棒性。

当前，为了提高感应电机的控制性能，有学者将滑模理论与MRAS理论相结合，应用于电机的状态观测。文献[11]基于传统的电压、电流模型构造出模型参考自适应系统，采用滑模变结构代替传统的PI控制器，估计出电机转速，提高转速观测精度及系统的抗干扰能力。文献[12]基于滑模理论分别在旋转坐标系下和静止坐标系下设计了两个滑模面，并据此构造了MRAS结构，实现了对转子磁链和转速的同时辨识。为克服一阶滑模结构的抖振问题，文献[13]基于Super-Twisting二阶滑模理论构造了滑模观测器，并设计了MRAS转速观测器。但文献[13]中，因含有纯积分环节，需要采用低通滤波器对幅值和相位加以补偿。

本文提出了一种基于二阶滑模观测器的MRAS型转速和磁链观测器。该方案是通过Super-Twisting二阶滑模观测器对所构造的中间变量进行观测，并将其观测结果直接作为参考模型，设计了一种MRAS结构来辨识转速。将获得的中间变量和转速信息用于转子磁链的观测，进而得到转子磁链角度，用于感应电机的磁场定向。所设计的观测器具有良好的动态性能和抗干扰能力。转速和磁链的辨识精度较高，保证了磁场定向的准确性，提高了矢量控制的性能。通过仿真实验验证了该方案的有效性以及良好的动稳态性能。

2 基于Super-Twisting的二阶滑模观测器

以定子电流和转子磁链作为状态变量，定子电压为输入量，则电机在两相静止坐标系下的数学模型可表示为[14]：

(1)

式中

β=Lm/(σLsLr)，η=1/Tr

k=1/(σLs)，k1=Lm/Tr

isα、isβ、ψrα、ψrβ以及usα、usβ分别为定子电流、转子磁链和定子电压；ωr为转子电角速度；Rs、Rr分别为定子电阻、转子电阻；Ls、Lr、Lm分别表示定子电感、转子电感和定转子间的互感；σ为漏磁系数；Tr为转子时间常数；p为微分算子。

为应用Super-Twisting理论进行滑模观测器的设计，令z1=isα，z2=isβ，并定义中间变量为：

(2)

将式(2)代入式(1)可得：

(3)

则电流观测器可构造如下：

(4)

(5)

(6)

式中，ε为边界层常数，为一合适的正数。

3 转子磁链观测器的设计与分析

3.1 转速的估计

由于机械时间常数远大于电气时间常数[3]，因此在构造速度观测器时可忽略速度变量的微分，则中间变量z3、z4的导数可以表示如下：

(7)

由式(1)中转子磁链方程可得：

(8)

将式(8)代入式(7)中，可得：

(9)

式(9)为所定义中间变量为状态量的可调模型，且ωr是待调节参数，则观测器方程如下：

(10)

将式(9)减去式(10)得：

(11)

式中

其中，J为反对称矩阵。根据Popov超稳定理论可知系统收敛的条件为：

(12)

(13)

式中，eω为误差信号，表达式为：

(14)

3.2 转子磁链观测器的设计

由中间变量的式(2)可以看出，转子磁链与中间变量和转速有关，在观测出中间变量和转速的基础上，可以得到转子磁链的观测值。由式(2)可以推出转子磁链的观测值如下：

(15)

在得到转子磁链观测值的基础上，进而可求出感应电机转子磁链的相角估计值为：

(16)

将此相角估计值用于坐标变换，即可实现基于直接转子磁场定向的感应电机矢量控制。该转子磁链观测器结构如图1所示。

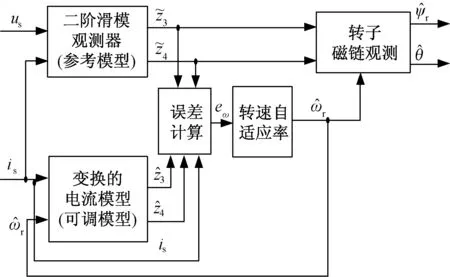
图1 基于二阶滑模的转子磁链观测结构图Fig.1 Second-order sliding mode based observer for rotor flux

4 仿真结果与分析

为验证该转子磁链幅值和角度观测方案的有效性，本文依据所构造的滑模观测器，设计了感应电机直接转子磁场定向矢量控制系统。图2为感应电机基于二阶滑模的直接转子磁场定向矢量控制系统的结构框图。其中开关打到1时代表的是系统工作在电流环模式。当开关打到2时代表的是系统工作在转速闭环模式。

图2 基于直接磁场定向的矢量控制系统Fig.2 Vector control system of induction motor based on direct field-orientation

在Matlab/ Simulink 环境中建立系统仿真模型，对方案进行仿真验证。所用电机参数为：电压380V，电流11.7A，功率5.5kW，极对数2，额定转速1460r/min，定子电阻1.022Ω，转子电阻1.334Ω，定子电感0.13341H，转子电感0.13341H，互感0.1284H。

当系统工作在电流环模式，即开关打到1时，系统的仿真结果如图3和图4所示。

图3为转速指令由500r/min阶跃变化到1000r/min的仿真结果。其中图3(a)是转速响应波形，图3(b)和图3(c)分别是转子磁链以及观测误差波形，磁链角度如图3(d)所示。

图3 电机转速突变时的仿真结果Fig.3 Simulation results for speed reference step up (500→1000r/min)

从图3(a)可以看出，当转速给定值由500r/min阶跃变化到1000r/min时，估计转速能很快地跟踪给定转速的变化，转速的动态响应性能良好。在转速突变过程中，转子磁链出现了瞬时波动，但很快收敛到实际值，稳态误差较小，磁链的观测精度较高，如图3(b)和图3(c)所示。图3(d)表明估计角度能很好地跟踪实际角度，角度观测较准确，对转速的变化具有较好的鲁棒性。

为了进一步验证本文所提出的转子磁链观测器对转子电阻变化具有较好的鲁棒性，在电机运行5s时使转子电阻Rr增大一倍，其仿真结果如图4所示。

由图4的仿真结果可以看出，在转子电阻突变的瞬间，转速估计值有较小波动，但很快收敛到实际值，转子磁链观测值也很快收敛于实际值，动态响应较快，估计角度与实际角度一致，磁链幅值保持不变，磁场定向较准确。由此可见本文设计的转子磁链观测器对转子电阻参数变化具有较强的鲁棒性，从而提高了感应电机矢量控制系统的性能。

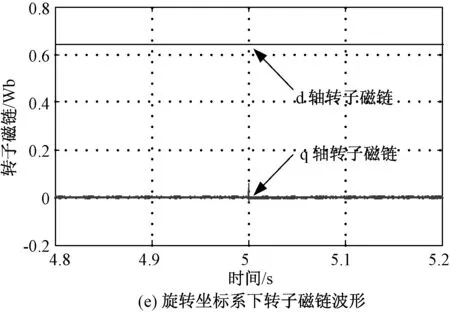
图4 转子电阻变化时的仿真结果(Rr→2Rr)Fig.4 Simulation results for rotor resistance step up

电机在运行过程中，转矩经常会发生变化，为了验证所设计的磁链观测器对转矩变化具有较好的鲁棒性，令图2中的开关打到2模式，系统工作在转速闭环，给定转矩由0阶跃变化到3N·m，仿真结果如图5所示。

从图5(a)的仿真结果可以看出在转矩突变情况下，转速出现快速变化过程，即便在此过程中，转速估计值也能够很好地跟踪其实际值的变化，且能较快恢复到给定转速。从图5(b)和图5(c)转子磁链以及磁链误差的仿真结果可以看出，在转矩突变瞬间，转子磁链观测值出现很小波动，但能快速恢复到实际值，且稳态误差很小且保持不变。角度估计值与实际值相符，如图5(d)所示。仿真结果表明所设计的观测器具有较强的抗负载扰动能力，转子磁链观测的准确度较高。

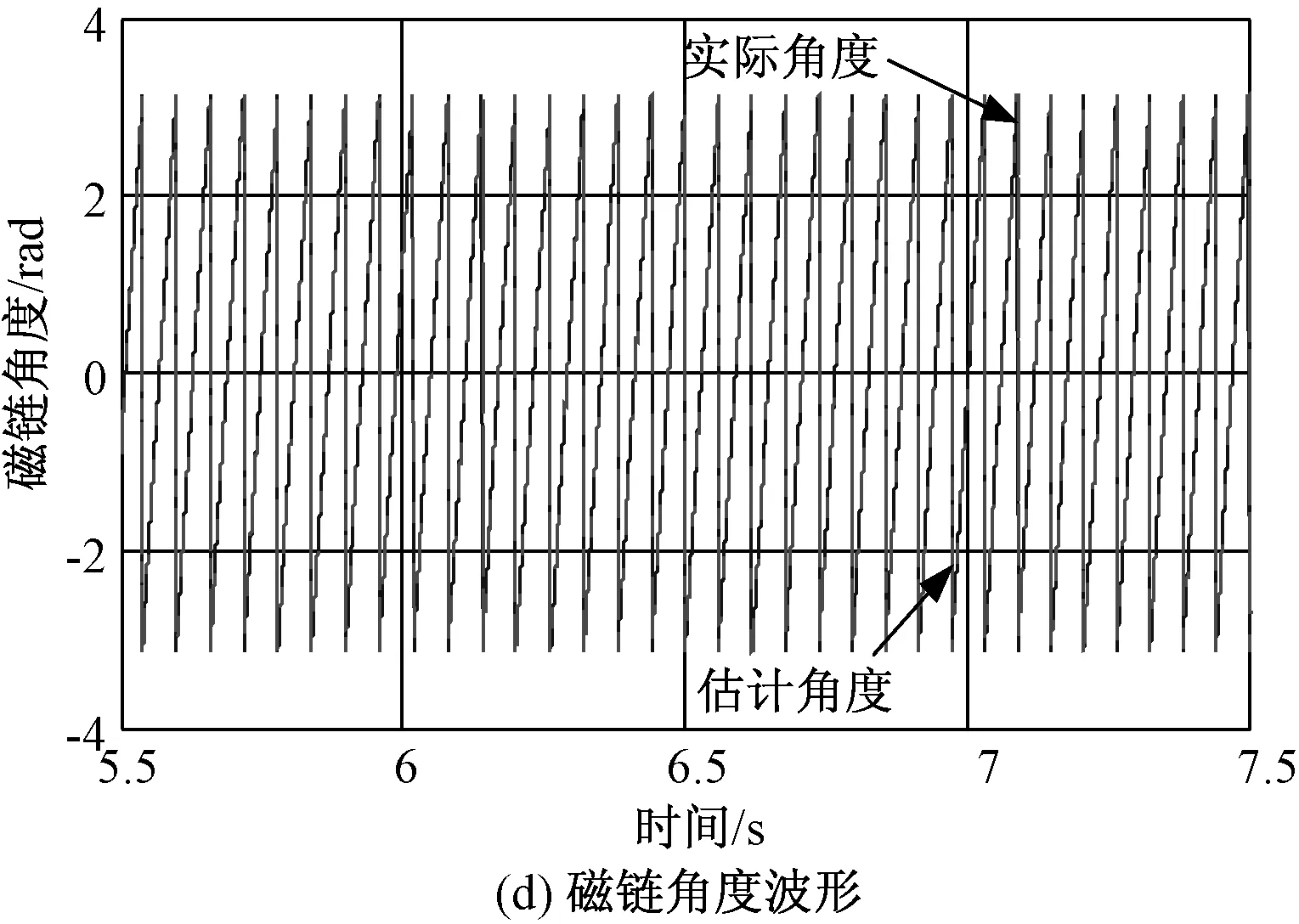
图5 电机转矩突变时的仿真结果 (转矩给定由0→3N·m)Fig.5 Simulation results for torque reference step up (0→3N·m)

5 结论

本文针对感应电机矢量控制系统，提出了一种基于二阶滑模的转子磁链观测方案。通过将二阶滑模观测器与电流模型相结合构造出新的MRAS结构，并根据Popov超稳定理论推导出转速自适应率，得到转速估计值。通过滑模观测器得到的中间变量以及估计的转速值计算出转子磁链，进而得到磁链角度，应用于感应电机的磁场定向。该方案采用二阶滑模观测器，并应用MRAS，转速的辨识结果较准确，转子磁链观测精度较高，对外部扰动和转子电阻的变化具有较强的鲁棒性。将转子磁链角度用于感应电机的矢量控制系统中，系统能在较宽的转速范围内稳定工作，并且具有良好的动稳态性能。仿真结果验证了该方案的有效性。

[1] 胡清, 王凯 (Hu Qing，Wang Kai). 一种感应电机磁链观测器的稳定性研究及改进(Stability improvements for closed-loop flux observer of induction machine)[J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2014，33 (12):15-19.

[2] 陆文斌, 姚文熙, 吕征宇(Lu Wenbin,Yao Wenxi,Lv Zhengyu). 基于改进闭环磁链观测器的感应电机无速度矢量控制(Speed sensorless vector control with improved closed-loop flux observer for induction machines)[J]. 电工技术学报(Transaction of China Electrotechnical Society), 2013,28(3):148-153.

[3] 许晓峰，许傲然(Xu Xiaofeng, Xu Aoran).异步电机无速度传感器矢量控制研究(Research on speed sensorless vector control of induction motors)[J].电力电子技术(Power Electronics), 2013,47(6):71-73.

[4] 史宏宇, 冯勇(Shi Hongyu, Feng Yong). 感应电机高阶终端滑模磁链观测器的研究(High-order terminal sliding mode flux observer for induction motors)[J]. 自动化学报(Acta Automatic Sinica), 2012,38(2):288-294.

[5] A B Proca, A Keyhani. Sliding-mode flux observer with online rotor parameter estimation for induction motors[J]. IEEE Transactions on Industrial Electronics, 2007, 54(2):716-723

[6] F Alonge, F D’Ippolito, A Sferlazza. Sensorless control of induction-motor drive based on robust Kalman filter and adaptive speed estimation[J]. IEEE Transactions on Industrial Electronics, 2014, 61(3):1444-1453.

[7] B Chen, W Yao, F Chen, et al. Parameter sensitivity in sensorless induction motor drives with the adaptive full-order observer[J]. IEEE Transactions on Industrial Electronics, 2015，62(7)：4307-4318.

[8] 陈伟，瞿文龙，陆海峰(Chen Wei, Qu Wenlong, Lu Haifeng).一种基于 MRAS 的异步电机速度辨识方法(A speed identification method for induction motor based on MRAS)[J].电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2006，25 (2):52-55．

[9] G Tarchala. Influence of the sign function approximation form on performance of the sliding-mode speed observer for induction motor drive[A]. 2011 IEEE International Symposium on Industrial Electronics (ISIE) [C]. Gdansk, Poland，2011.1397-1402.

[10] P T Doan, T L Bui, H K Kim, et al. Sliding-mode observer design for sensorless vector control of AC induction motor[A]. 2013 9th Asian Control Conference, ASCC 2013 [C]. Istanbul, Turkey, 2013.1-5.

[11] W Lei, Y H Li, X Lei. Sliding mode variable-structure MRAS speed identification for induction motor direct torque control system[A]. 2009 Second ISECS International Colloquium on Computing, Communication, Control, and Management [C]. Sanya, China, 2009.59-62.

[12] M Comanescu. An MRAS-type estimator for the speed, flux magnitude and rotor flux angle of the induction motor using sliding mode [A]. 2014 International Symposium on Power Electronics, Electrical Drives, Automation and Motion [C]. Ischia, Italy,2014.719-724.

[13] 黄进,赵力航,李炳楠,等(Huang Jin, Zhao Lihang, Li Bingnan, et al.).异步电机转子磁链观测与转速辨识的方法(A method for induction motor rotor flux observation and rotational speed identification)[P].中国专利(Chinese Patent)： CN201210486855.0,2013-2-13.

[14] L Zhao, J Huang, H Liu, et al. Second-order sliding-mode observer with online parameter identification for sensorless induction motor drives[J]. IEEE Transactions on Industrial Electronics, 2014, 61(10):5280-5289

Second-order sliding mode observer for rotor flux of induction machine

XU Jing， YANG Shu-ying， GUO Lei-lei， ZHANG Xing

(School of Electrical Engineering and Automation, Hefei University of Technology,Hefei 230009, China)

The basis of vector control is to obtain the speed and rotor flux information accurately. In this paper, a new method based on a second-order sliding mode (SSM) observer for rotor flux is presented. The observer is constructed by combining a SSM observer with a design on model reference adaptive system (MRAS), and the SSM observer designed with the Super-Twisting algorithm is used as the reference model for the defined variable, while the adaptive model on the rotor speed comes from the current model of the flux. By means of the MRAS design, the rotor speed is observed. On the basis of this, the rotor flux and angle is calculated, and then the vector control of induction motor based on direct field-oriented is implemented. Since the MRAS is constructed directly on the defined variable, the pure integrator for flux calculation is avoided thoroughly, benefiting implementation of the observer. Meanwhile, the SSM observer can not only reduce the chattering disturbance in the first-order SM observer to a great extent, but also enhance the robustness to parameter. Simulative results show that the observer of rotor flux not only has high accuracy, but also is robust to the load disturbance and rotor parameters perturbation, and the stability and accuracy of the system is improved.

induction motor; second-order sliding mode; MRAS; flux observation; sensorless control

2016-03-23

徐 静(1990-)， 女， 安徽籍， 硕士研究生， 研究方向为电力电子与电力传动； 杨淑英(1980-)， 男， 安徽籍， 副教授， 博士， 研究方向为风力发电及电机驱动控制技术。

TM343

A

1003-3076(2016)12-0032-06