车辆荷载作用下双曲拱桥的动力响应实测与分析

刘建军

(1. 现代投资股份有限公司, 湖南长沙 410000; 2. 湖南大学土木工程学院, 湖南长沙 410000)



车辆荷载作用下双曲拱桥的动力响应实测与分析

刘建军1, 2

(1. 现代投资股份有限公司, 湖南长沙 410000; 2. 湖南大学土木工程学院, 湖南长沙 410000)

【摘要】文章首先介绍车桥动力相互作用的相关理论,具体内容包括：桥梁固有振动理论、静力分析理论、阻尼理论、车桥动力相互作用理论等。然后运用大型桥梁分析软件MADIS对工程实例进行了动力分析，并将计算结果与实验结果进行对比，以验证应用MADIS建模及进行车桥动力相互作用分析的可行性。所得结果对桥梁抗震设计有一定的参考作用。

【关键词】双曲拱桥；车辆荷载；自振频率；动力响应

现今有关双曲拱桥在汽车荷载下的动力反应研究的较少。我国现行桥梁设计规范将汽车荷载作用的冲击系数定义为桥梁基频的函数，比原规范有了很大的改进，然而对整个桥梁应用单一的冲击系数不尽合理，桥梁不同位置的动力反应是不同的，应规定不同的冲击系数；而且作为冲击系数效应值的评价尺度是着眼于弯矩还是挠度也是研究的课题。此外，规范亦没有考虑阻尼、车辆模型、车辆运行速度等对桥梁冲击系数的影响。

由于影响车桥振动的因素很多，通过桥梁的汽车荷载的流量大小、车辆间距、轴重、行驶速度、车辆的行驶位置、车辆的动力持性等均有明显的随机性，是无法预知的。同时，路桥连接缝的结构状态、桥头引道及桥面的平整状态也具有明显的随机性，这给车辆对桥梁结构动力作用的理论分析带来了很大困难。因此，在车桥耦合振动分析中，一般多通过桥梁结构的动荷载试验来测定上述因素的综合作用结果，同时采取必要的理论分析加以验证。如何从理论上确定车辆荷载下公路桥梁的动力响应，一直为工程界所关注。

1车辆桥梁相互作用的分析方法

1.1车辆桥梁相互作用的研究任务

车振、地震及风振是桥梁结构动力学的三个主要问题。桥梁结构在行车作用下，由于汽车与桥梁结构的相互作用引起车辆桥梁整体系统的振动，属于典型的快速时变结构力学范畴。汽车桥梁系统的振动，使得桥梁结构的内力和变形大于静力车辆荷载作用下的结构内力和变形。为了确保桥梁在车辆运行时的结构安全，在桥梁设计中必须考虑车辆荷载动力效应的影响。在目前世界各国桥梁设计规范中，一般用动力放大系数亦称冲击系数来考虑车辆荷载对桥梁结构产生的动力效应。车辆与桥梁相互作用领域研究的主要任务就是研究车辆桥梁整体系统的动力行为。对于车辆桥梁系统的振动问题，由于汽车及桥梁结构两者都是具有刚度、质量和阻尼的振动系统，并且在车辆运行时，作用在桥梁上的汽车车轮位置随时间发生变化，从而使得汽车桥梁系统的振动问题相当复杂。影响汽车桥梁系统动力行为的主要因素包括以下几个主要方面：

(1)桥梁结构的自振频率特征由桥梁结构的刚度和质量确定；

(2)汽车车辆的自振频率特征由汽车车辆的刚度和质量确定；

(3)桥梁结构及车辆系统的阻尼；

(4)汽车在桥上运行的速度；

(5)桥面的不平顺；

(6)汽车上桥时的初始运动状态。

车辆桥梁系统的动力行为是空间问题，包括垂直方向的振动和水平方向的振动；在激励方式上，除汽车正常的运行外，还有汽车的起动与刹车等；在研究方法上可分为确定性振动分析和随机振动分析两大类。

在确定性振动分析方面，最基本的是单自由度振动微分方程，根据牛顿第二定律及达朗贝尔原理建立如下：

(1)

式中:v(t)为质量m在时间t的位移；m、c、k分别为系统的集中质量、阻尼系数及弹簧刚度;F(t)为随时间变化的外荷载。

随机振动分析采用概率统计方法确定系统动力反应的统计特征。

1.2车桥动力相互作用相关理论

1.2.1固有振动理论

固有振动反映振动系统的固有特性，是研究一切振动问题的基础。所谓固有振动是指弹性系统在没有外部动力的作用下形成的振动。求解固有振动的频率从数学上说属于求特征值的问题。

有限元法是现今比较常用的方法。利用有限元，结构的固有振动可归结为下列广义特征值问题:

(2)

式(2)中刚度矩阵[K]和质量矩阵[M]都是对称矩阵，[K]通常是正定的。[M]是满阵，如果只有节点集中质量，那么[M]是对角阵。如果[K]及[M]有n阶，则可求得n个频率ω及n组振型{x}。把式(2)两边都左乘以[K]-1，并乘λ=1/ω2，得：

(3)

将[K]-1[M]用[A]表示，于是得：

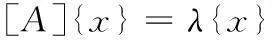
(4)

这是一个“标准特征值问题”，式中[A]在通常情况下是对称矩阵。但在某些情况下，[K]-1[M]不是对称矩阵，此时为了便于计算，常常把它转化成标准特征值问题。

接下来对[K]进行三角化分解，使

(5)

式 (5)中[L]是上三角矩阵，于是

(6)

代入式(3)得:

(7)

两边左乘[L]，得:

(8)

令Z=[L]{x}，代入上式得:

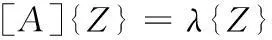
(9)

式子中[A]=[L]-1[M][L]

[A]是对称矩阵，上式就是一个标准特征值问题。求得特征向量{Z}后，容易利用{Z}=P[L]{x}还原成方程式(2)的特征向量{x}，即:

(10)

标准特征值问题的解法有很多种，常用的有雅可比法、子空间迭代法、乘幂法及反乘幂法、G—H法、Ritz向量法、Lanczos法。本文采用子空间迭代法，用大型桥梁分析软件MADIS加以实现。

1.2.2静力分析理论

结构的静力平衡方程组为:

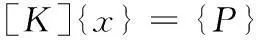
(11)

即以节点位移为基本未知量的系统节点平衡方程组。式中[K]、{x}、{P}分别表示结构刚度矩阵、节点位移向量、节点荷载向量。可以用直接解法求解此类方程组。直接解法以高斯消去法为基础，求解效率高。在方程组的阶数不是特别高时(例如不超过10 000阶)，通常采用直接解法。常用方法有等带宽高斯消去法、三角分解法以及以上述两法为基础，适用于更大型方程组求解的分块解法和波前法。波前法求解的特点是：刚度矩阵[K]和荷载列阵{P}不按自然编号进入内存而按计算时参加运算的顺序排列，在内存中只保留尽可能少的一部分[K]和{P}中的元素。在波前法中,方程被处理的次序由单元编号来确定，而不是由节点编号来确定。要消去的第1个方程只是与单元1相关的那些方程。接着，相邻单元2的刚度矩阵的贡献加到方程组中，假使仅是单元1和单元2对附加的自由度有贡献，即没有其他单元对这些自由度的刚度矩阵有贡献，那么这些方程从方程组中被消去。当一个或更多单元对方程组有贡献时，只是由这些单元贡献的附加自由度将从解中被消去。在组合和解之间的这种反复交替最初被看作波前，这个波在结构上以单元编号的样式扫荡。由于这种方法的较大有效性，在结构上将以跨越最少节点号的方向进行连续的单元编号。本文在静力分析中还考虑了桥梁结构的几何非线性。引起结构非线性的原因很多，它可以被分为三种主要类型：

(1)状态变化。许多普通结构表现出一种与状态相关的非线性，例如，一根只能拉伸的电缆可能是松散的，也可能是绷紧的。这些系统的刚度由于系统状态的改变在不同的值之间突然变化。

(2)几何非线性。如果结构经受大变形，它变化的几何形状可能会引起结构的非线性响应。

(3)材料非线性。非线性的应力-应变关系是结构材料非线性的常见原因。许多因素可以影响材料的应力-应变性质，包括加载历史、环境状况、加载的时间总量等。

1.2.3阻尼理论

桥梁结构的阻尼是确定桥梁振动的重要动力参数之一。阻尼消耗能量，使振动衰减，对桥梁的安全是有利的。阻尼的大小直接关系到桥梁在动荷载作用下振动的强弱，因此研究桥梁的阻尼规律是提高桥梁动力计算精确度的关键之一。

形成桥梁结构阻尼的因素十分复杂，大致可以分为下列三类：

(1)材料的内阻尼。由振动时材料分子间的内摩擦力所形成。

(2)摩擦阻尼。由结构物支承及连接处的摩擦力等所形成，又称干摩擦阻尼或库伦阻尼。

(3)空气介质阻尼。由周围空气介质对结构物运动的阻力所形成。

材料内阻尼使振动按指数随时间衰减，而桥梁结构的摩擦阻尼则使振幅按直线随时间衰减，二者作用的性质不同。至于空气介质阻尼作用的性质则大致与材料内阻尼相似。桥梁结构的振动阻尼还不能像固有频率那样准确计算出来，在振动分析中常参考一些桥上实测资料来近似取值。考虑到实际情况和计算上的方便，在桥梁振动计算中通常采用Rayleigh阻尼，又称为比例阻尼，是最常用也是比较简单的阻尼，它是多数实用动力分析的首选，对许多实际工程应用也是足够的。Rayleigh假定阻尼矩阵[C]为质量矩阵[M]和刚度矩阵[K]的线性组合，即[C]=α[C]+β[K], 是α阻尼和β阻尼之和。已知结构总阻尼比是ξ，则用两个频率点上α阻尼与β阻尼产生的等效阻尼比之和与其相等，即

(12)

这样就可以求出近似的α阻尼与β阻尼系数。

1.2.4车桥动力相互作用理论

当汽车以一定的运行速度通过桥梁时，车辆位置随着时间变化，并且汽车车辆和桥梁结构都是具有刚度、质量及阻尼的振动系统，因而汽车与桥梁相互作用问题非常复杂。一般来说，首先分别建立汽车和桥梁的振动方程，然后考虑车轮与桥梁的位移协调条件，建立汽车与桥梁相互作用的整体系统方程，采用数值方法求解整体系统方程。

车辆单元的运动方程为：

(13)

式中：mt、ct、kt、ft分别为车辆单元的质量矩阵、阻尼矩阵、刚度矩阵、荷载向量。

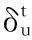
(14)

车辆与桥梁相互作用的车桥耦合单元运动方程为:

(15)

式中各矩阵和向量的详细表达式为:

(16)

式中各矩阵的含义如下：

mbb为车桥耦合单元的质量矩阵；

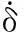
δb为车桥耦合单元的位移向量；

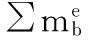
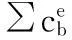
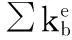
Nb为桥梁单元的形函数；

r为桥面的不平顺函数；

v为车辆的水平运动速度；

a为车辆的水平运动加速度；

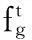
根据建立的车桥耦合单元，可以采用有限元方法形成汽车桥梁整体系统的质量矩阵、阻尼矩阵、刚度矩阵和荷载向量。由于汽车运行通过桥梁时，作用在桥梁上的车轮位置随着时间而变化，因此汽车桥梁整体系统的质量矩阵、阻尼矩阵、刚度矩阵及位移向量、速度向量、加速度向量和荷载向量均随时间而变化，也就时说，对于每一个时间增量，汽车桥梁整体系统的运动方程必须重新更改。按照有限元方法形成汽车桥梁整体系统方程如下：

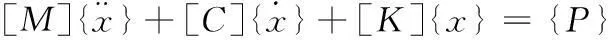
(17)

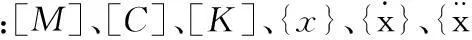
车桥动力相互作用计算方法有分组迭代法和整体求解法两种。分组迭代法就是将汽车桥梁系统方程分为车辆方程和桥梁方程两组分别进行迭代，然后再考虑车轮桥梁位移协调条件，进行反复迭代，最终求解汽车桥梁系统方程的结果;整体求解法就是直接形成汽车与桥梁整体系统的方程，采用数值方法如Wilson-θ法和Newmark法等求解。整体求解法比分组迭代法运算速度快，但要求的计算机内存更大一些。车轮与桥梁接触条件主要考虑两个因素，即桥面不平和车轮与桥梁位移协调条件。桥面不平是车辆与桥梁相互作用问题的主要激励因素;车辆与桥梁位移协调条件就是假定汽车运行通过桥梁时，车轮与桥梁始终保持接触。

2工程实例分析

2.1工程概况

某大桥建成于1978年，所在路线依1972年颁发的《公路工程技术标准》(估计为四级公路，相应设计荷载为汽车-10级，履带-50。桥位桩号为K5+100，桥长178.8 m，总桥宽7 m，2车道。上部结构形式为25 m(板拱)+3×40 m(双曲拱)，浆砌片石；下部结构形式为U型桥台、重力式桥墩、扩大基础。该桥设计图纸及施工资料暂未找到(图1)。

图1　桥立面图

2.2动载试验方案

(1)在夜间(晚上12：00～早晨4：00)进行地脉动实验，测试桥梁的竖向自振特性；

(2)跑车实验：一辆重车(15 t)分别以30 km/h、40 km/h的速度驶过主桥，测试桥梁的竖向强迫振动特性；

(3)仪器采用由拾振器(位移、速度与加速度传感器)、数据采集仪、电荷放大器及动力分析仪组成的动力测试系统。

全部数据采集与分析采用德国生产的国际公认的HBM动力测试与分析系统完成。

2.3试验结果与分析

2.3.1理论分析

通过桥梁分析软件MIDSA对该桥进行计算，前10阶振型见图2～图11,各跨的前10阶理论自振频率见表1。

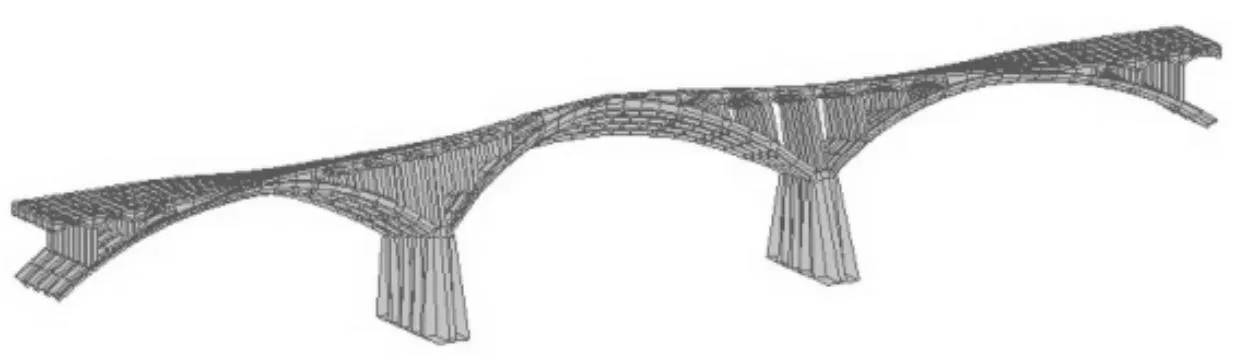
图2　第1阶振型

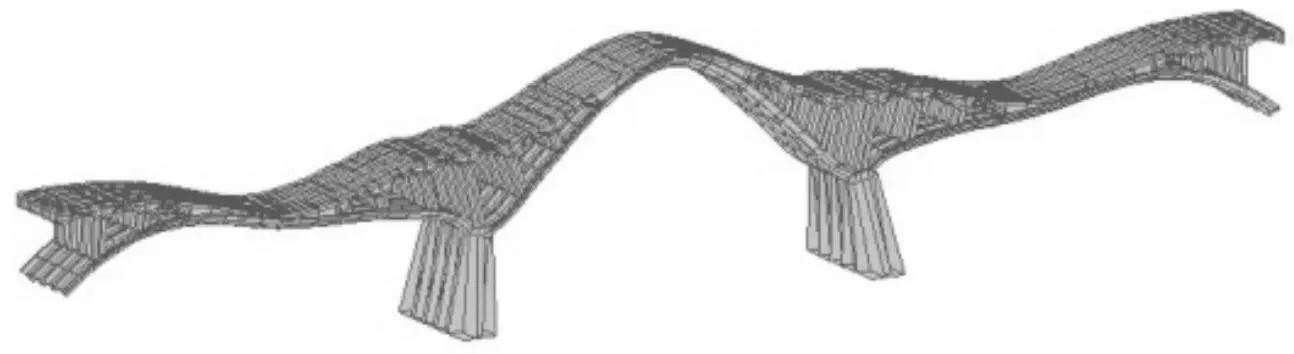
图3　第2阶振型

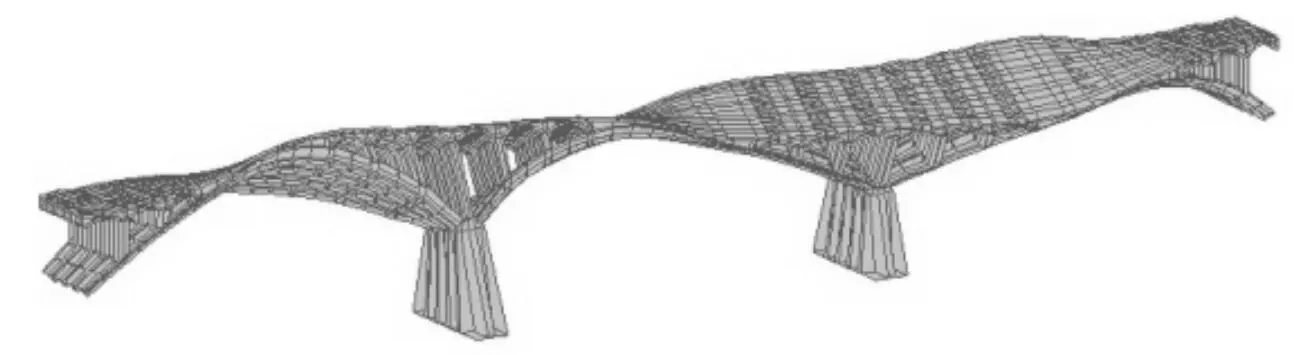
图4　第3阶振型

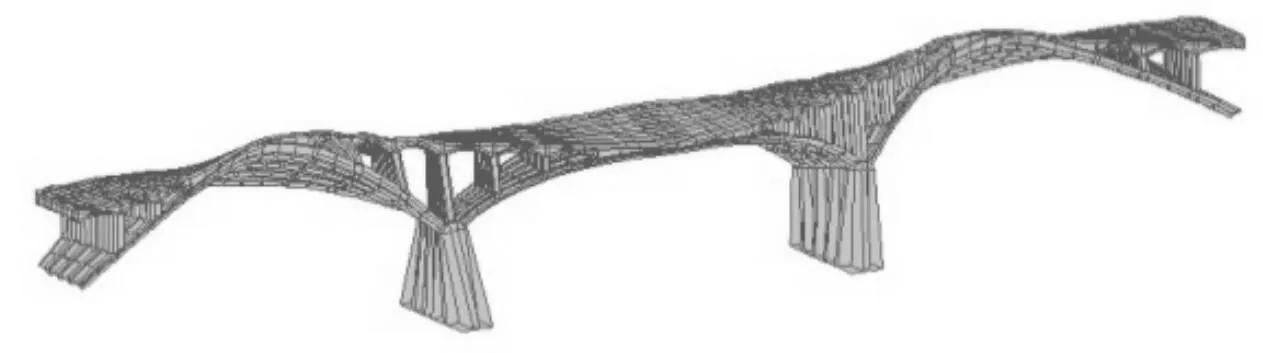
图5　第4阶振型

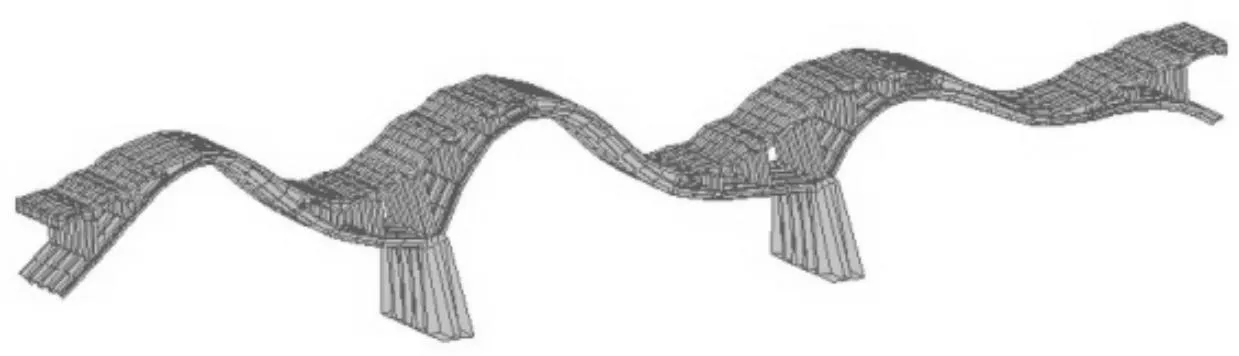
图6　第5阶振型

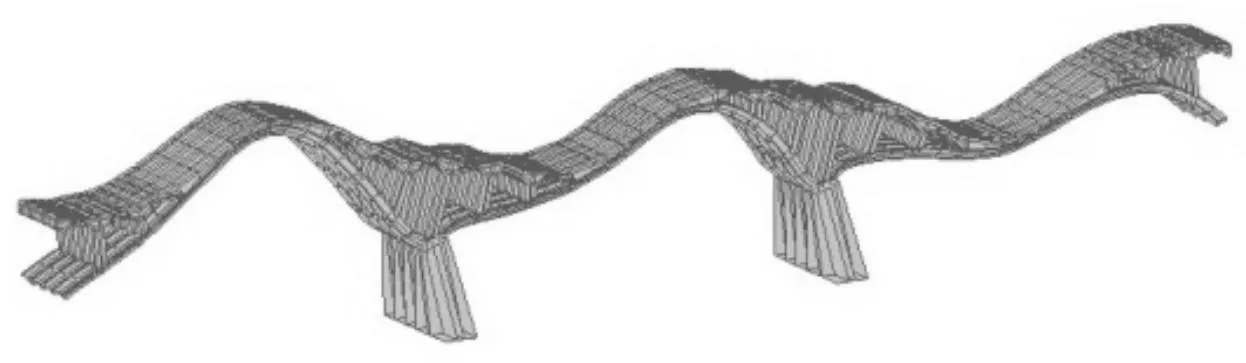
图7　第6阶振型

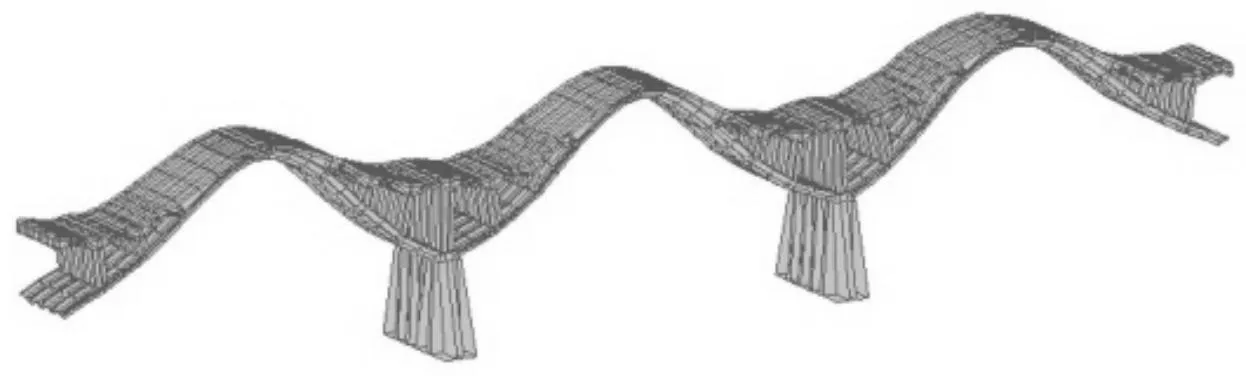
图8　第7阶振型

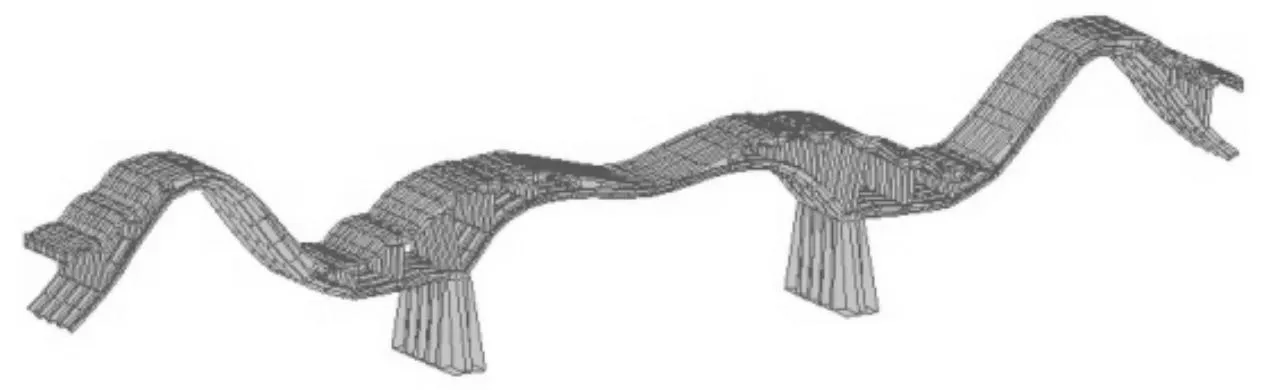
图9　第8阶振型

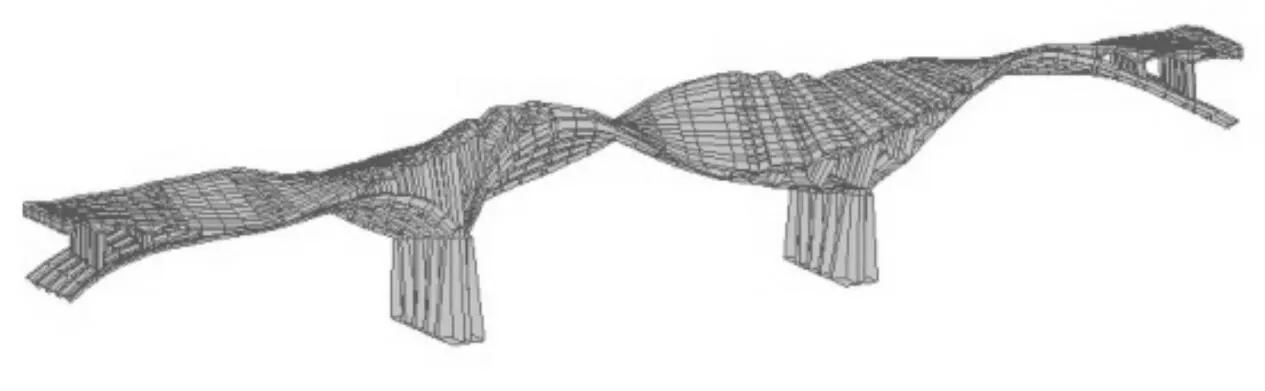
图10　第9阶振型

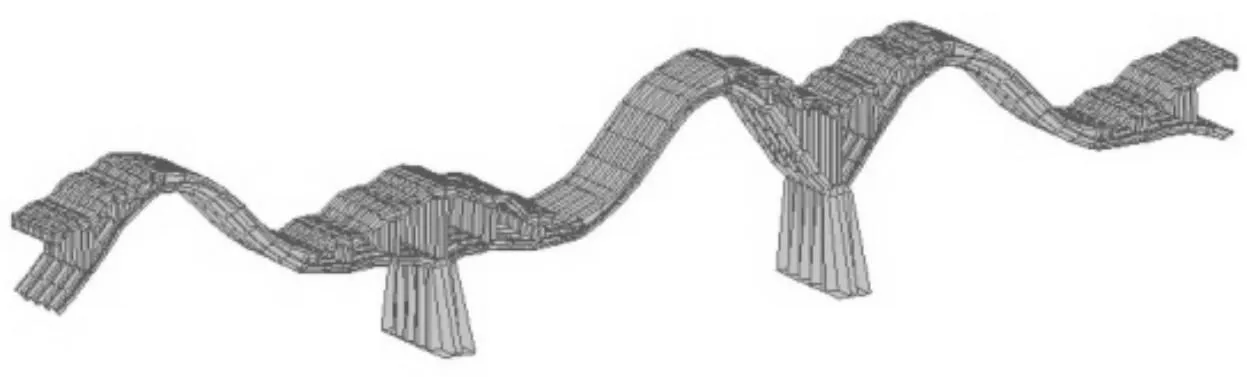
图11　第10阶振型

综合跑车及环境随机振动的测试数据，可得到精确而真实的桥跨结果自振特性数据。

2.3.2动载试验分析结果与评定

(1) 桥梁自振频率测试结果与分析见表2、图12。

由以上可知各阶自振频率的实测值与理论值基本一致，但理论频率小于实测频率，说明实际结构刚度小于设计刚度。

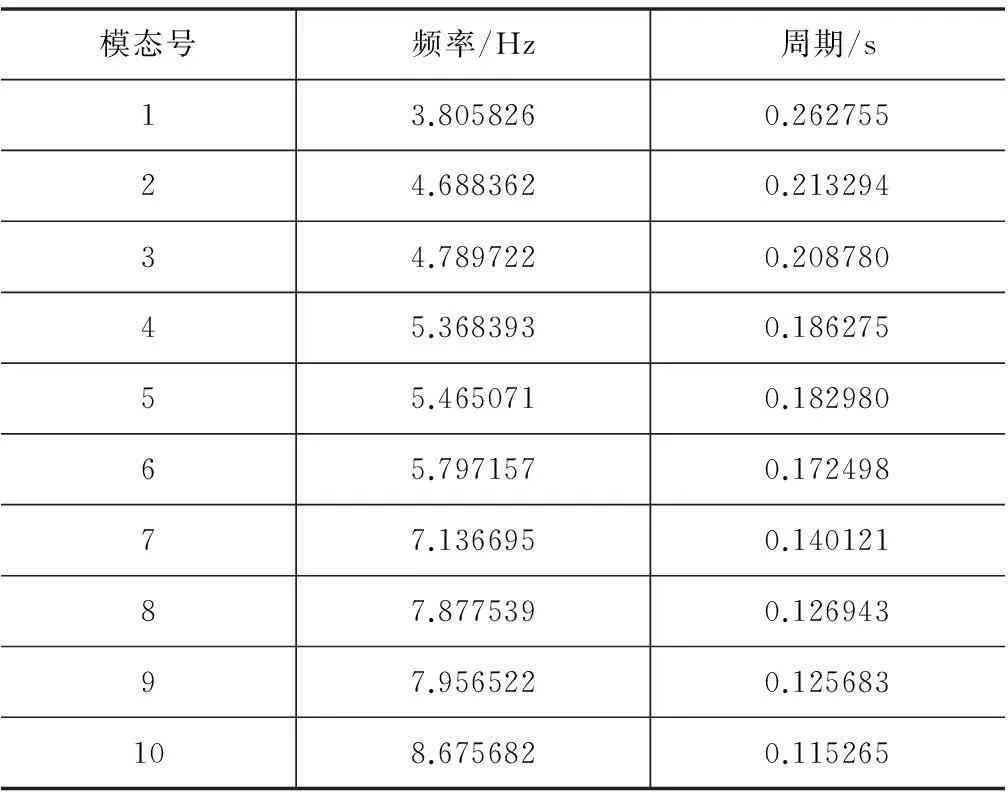
表1　自振特性理论分析

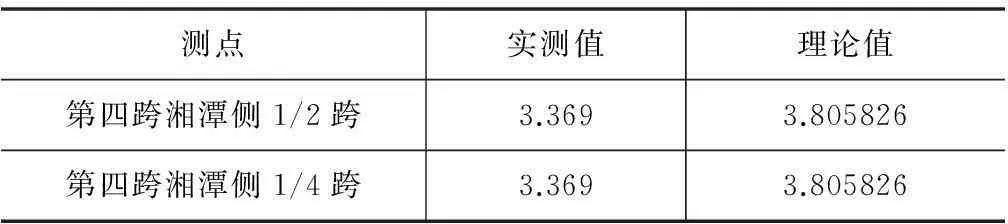
表2　测试频率与理论频率比较

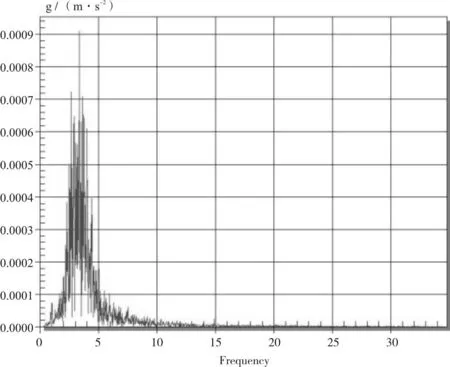
(a)脉动第四跨1号测点加速度频谱

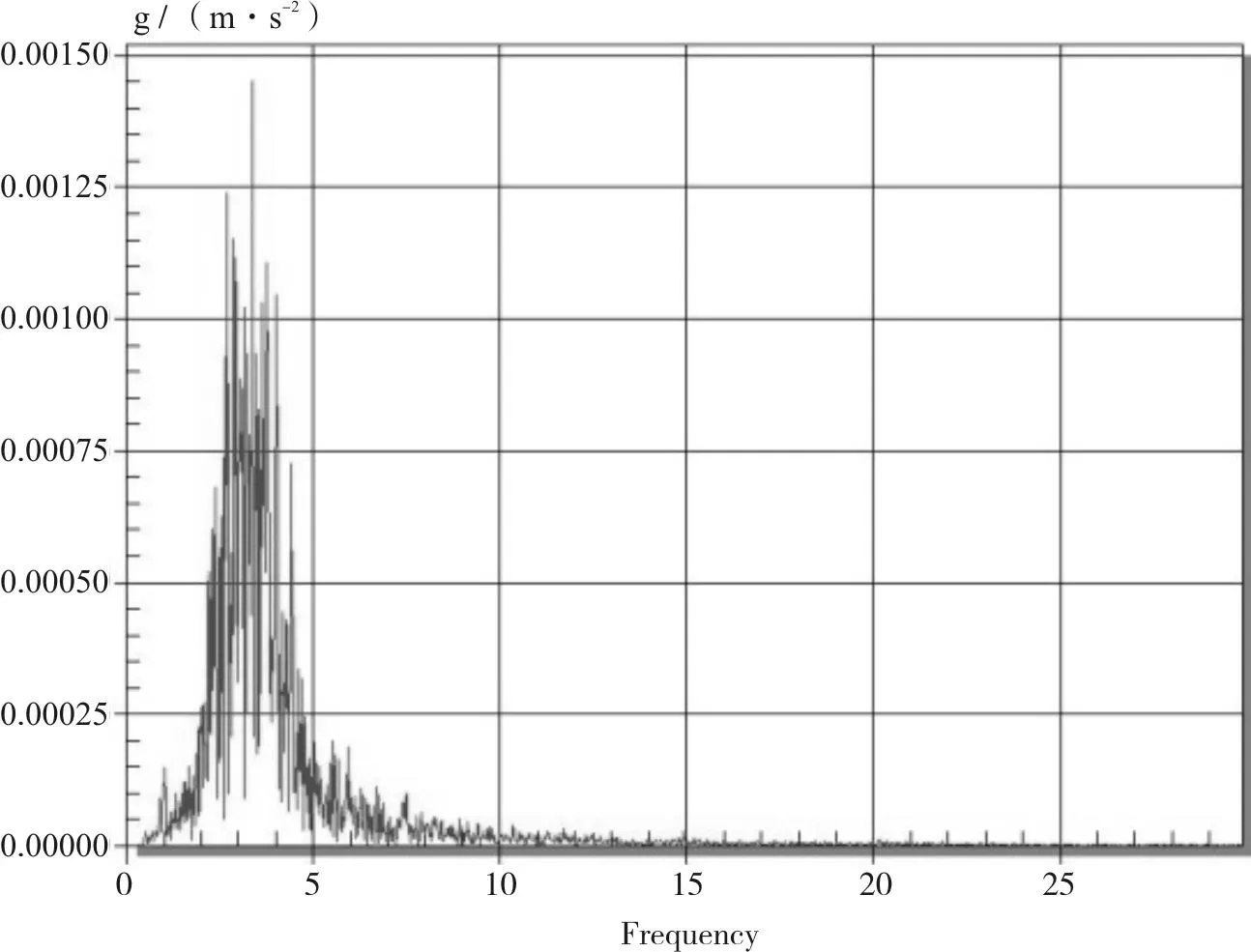
(b)脉动第四跨2号测点加速度频谱图12　环境激振(脉动)测点频谱

(2)桥梁车振频率测试结果与分析见表3、图13、图14。

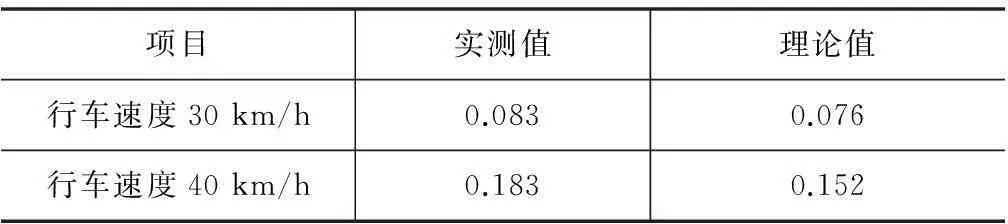
表3　主桥中跨跨中竖向位移的冲击系数理论值及实验结果

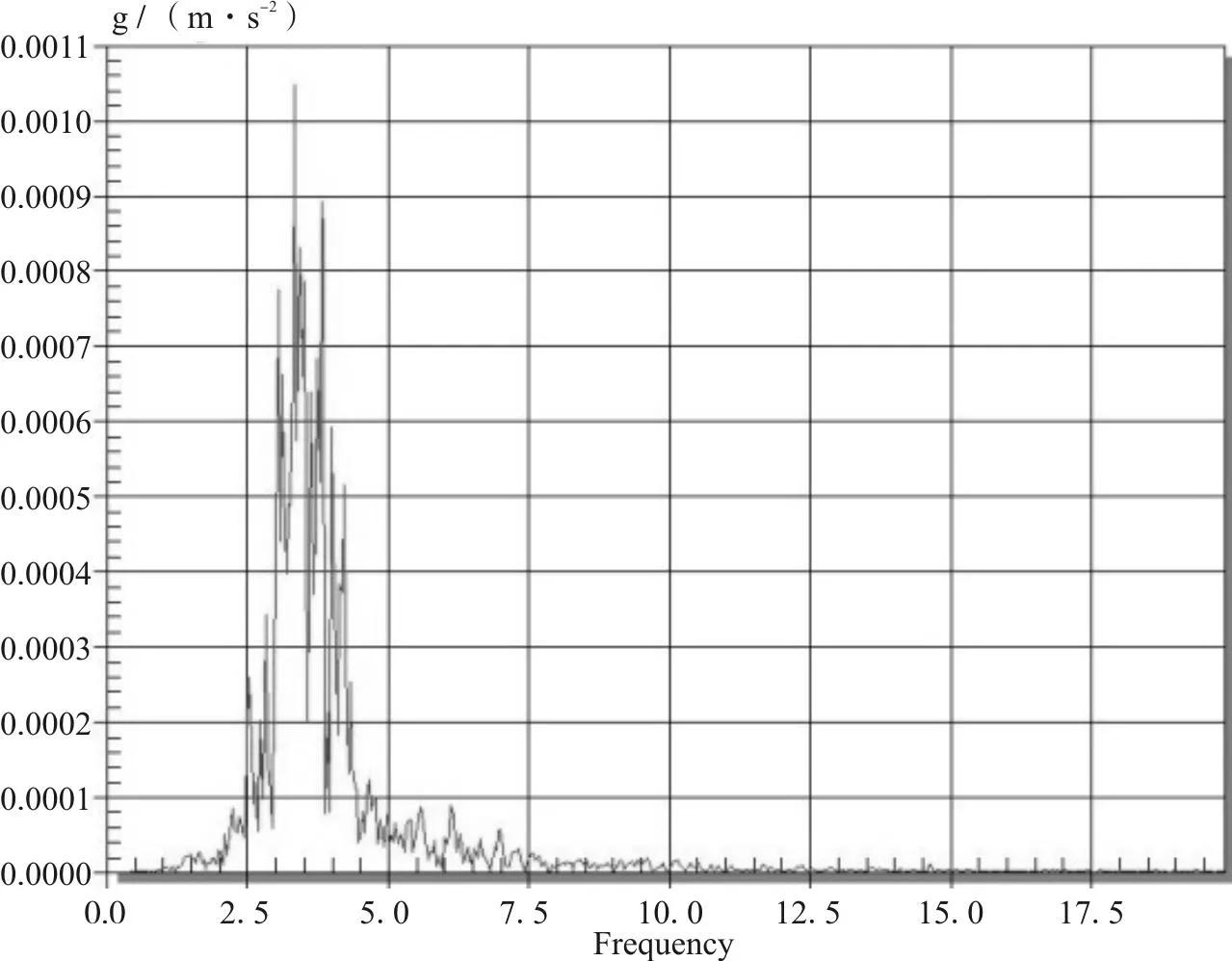
(a)时速30 km/h第四跨1号测点加速度频谱

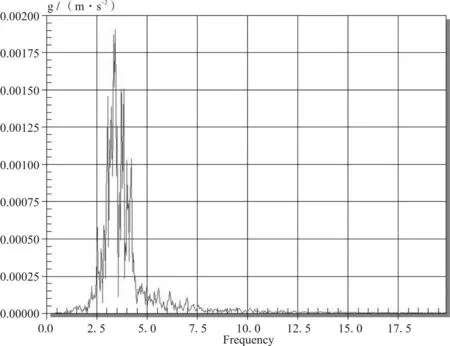
(b)时速30 km/h第四跨2号测点加速度频谱图13　跑车速度为30 km/h时各测点的加速度频谱

根据现场考察，选取了具有代表性的两跨作为实验对象，分别采用跑车、环境激振两种方法进行动力测试，并对测试数据进行了频谱分析，全部数据采集与分析采用德国生产的国际公认的HBM动力测试与分析系统完成；同时用大型商用桥梁结构分析软件Midas建立了动力分析模型，得到了各跨的理论分析频率。将实测频率值与理论分析值进行对照，得出实测频率略小于理论分析频率值，这主要是由于混凝土开裂，削弱了截面的面积，致使桥梁的刚度下降，从而导致实测桥梁频率降低。

3结论

(1)试验数据与理论数据基本一致，说明本文所采用桥梁车辆动力响应分析方法是可行的。

(2)理论数据较试验数据偏大，说明桥梁结构刚度与其使用时间明显相关，使用时间越长，刚度越低。故对超过一定年限的桥梁应定期进行维护加固处理。

(3)桥梁车辆车载动力响应受车辆流量大小、车辆间距、轴重、行驶速度、车辆的行驶位置、车辆的动力持性等多方面因素有关，在桥梁设计计算中，应综合考虑各方面因素，取最不利情况进行设计。

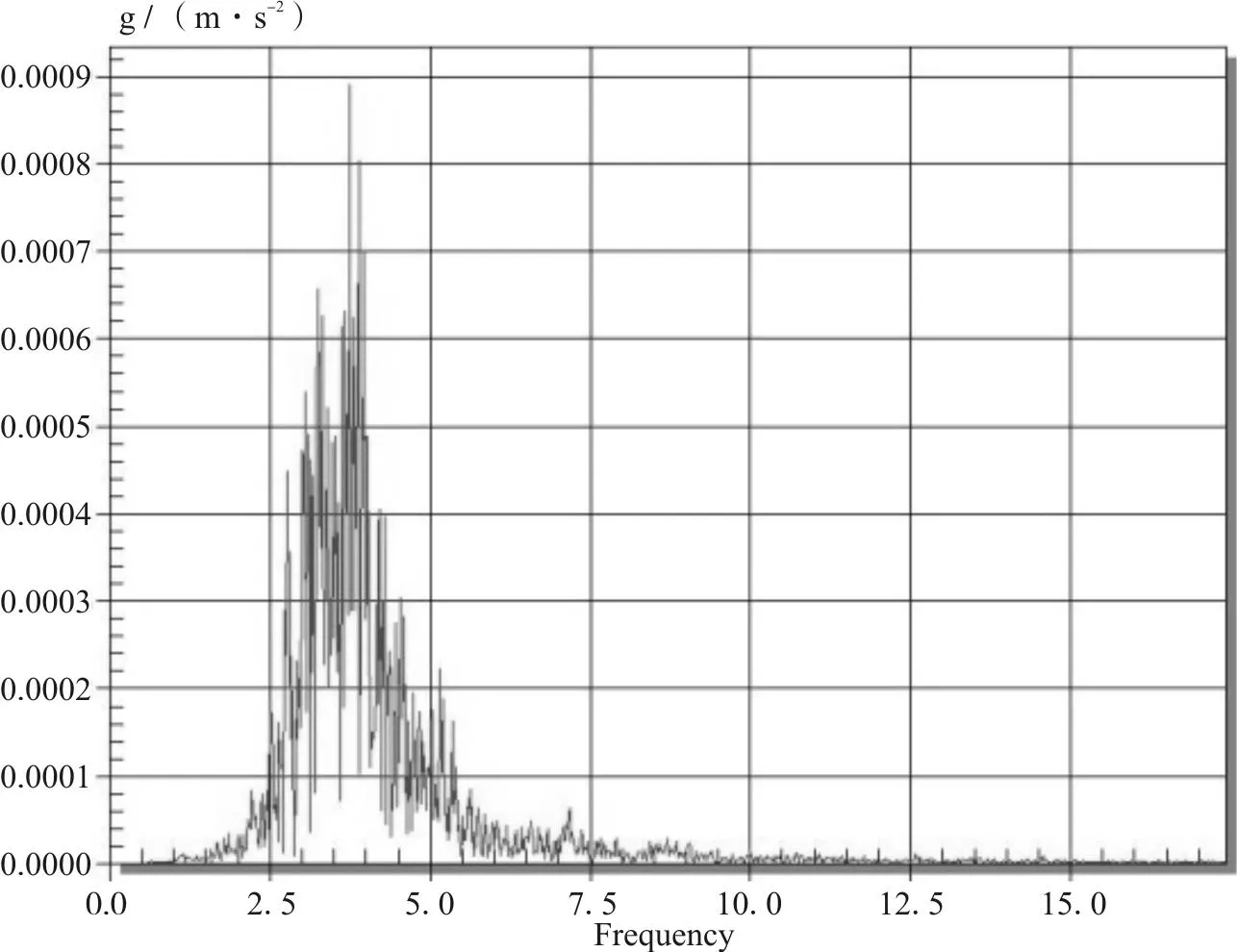
(a)时速40 km/h第四跨1号测点加速度频谱

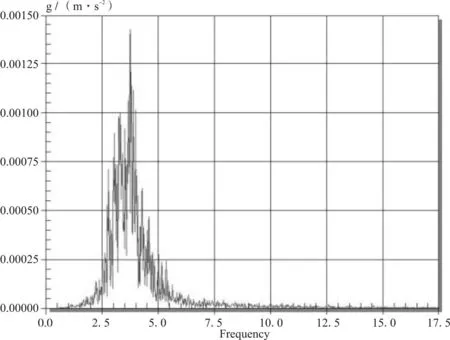
(b)时速40 km/h第四跨2号测点加速度频谱图14　跑车速度为40 km/h时各测点的加速度频谱

(4)相对其他类型桥梁，双曲拱桥整性较差，整体刚度小，在抗震设计中应加以考虑。

参考文献

[1]李国豪.桥梁结构稳定与振动[M].北京：中国铁道出版社，1992.

[2]范立础，胡世德，叶爱君.大跨度桥梁抗震设计[M].北京：人民交通出版社, 2001.

[3]范立础.桥梁抗震[M].上海：同济大学出版社，1997.

[4]田苗苗.公路桥梁在行车荷载下的振动研究[D].郑州大学，2005.

[5]罗浩，郭向荣.大跨度提篮拱桥车桥耦合振动分析[J].振动与冲击，2008(12).

[6]王永平，陈彦江，傅金科.车队荷载作用下简支梁桥动力响应的实验与理论研究[J].工程力学，1995(增刊).

[7]王元丰，许士杰.桥梁在车辆作用下空间动力响应的研究[J].中国公路学报，2000(4).

[8]JTG/T B02-01-2008 公路桥梁抗震设计细则[S].

[9]赵青.移动双轴汽车荷载作用下桥梁动力特性的数值模拟[J].安徽建筑工业学院学报，2006(2).

[10]卜建清，刘宪福.基于桥梁动力响应的车-桥接触力识别方法[J].石家庄铁道学院学报，2006(4).

【文献标志码】A

【中图分类号】U448.22+1

[作者简介]刘建军(1979～)，男，土家族，博士研究生，工程师。

[定稿日期]2014-05-08