基于最小二乘支持向量机的低渗透油藏调剖效果预测

赵燕红，马驷驹，刘小平，景文杰，张召召（.西安长庆化工集团有限公司研究所，陕西西安　7008；.中国石油长庆油田分公司第三采油厂，宁夏银川　750006）



基于最小二乘支持向量机的低渗透油藏调剖效果预测

赵燕红1，马驷驹2，刘小平2，景文杰2，张召召2
（1.西安长庆化工集团有限公司研究所，陕西西安710018；2.中国石油长庆油田分公司第三采油厂，宁夏银川750006）

摘要：调剖效果受油藏地质条件、开发状况和调剖工艺等诸多因素影响，调剖效果预测实质上是解决一个多因素共同作用的复杂非线性问题。常规的数值模预测对地质建模准确性要求高、历史拟合时间长而不能满足实际应用需求。本文提出利用最小二乘支持向量机法构建调剖效果与其主控因素之间的非线性映射模型，将未知井调剖效果预测转化为非线性函数的求解过程。以靖安油田五里湾区块24口调剖井资料为学习样本，建立了计算调剖后井组增油量、降水量的最小二乘支持向量机预测模型并进行了验证。结果表明，计算结果与实际值拟合精度较高、误差较小，该方法可用于矿场调剖效果预测与评价。

关键词：调剖效果；影响因素；最小二乘支持向量机；预测模型；五里湾区块

影响调剖效果的因素涉及油藏条件、开发状况和调剖工艺等三大类中的诸多小类[1-4]，因此，调剖效果预测实质上成为解决一个多因素共同作用的复杂非线性问题。目前，广泛采用数值模拟法进行调剖效果的预测[5-7]，该方法对地质建模准确性要求较高、历史拟合耗时较长，往往不能满足实际应用的需求。本文利用基于统计学习理论的支持向量机（Support Vector Machine，SVM）方法进行调剖效果预测。SVM基于Vapnik的结构风险最小化原理，具有结构简单、泛化能力强、求解速度快等特点，在解决小样本、非线性、多维问题方面优势显著[8-13]。最小二乘支持向量机（least squares support vector machine，LSSVM）是标准支持向量机的改进，采用等式约束代替标准支持向量机中的不等式约束，并将求解二次规划问题转化为直接求解线性方程组，大大降低了计算复杂程度。对于调剖效果与各影响因素的复杂关系，LSSVM通过核函数将样本空间映射到特征空间中求出原样本集的最优化分类面，进而得到输入变量（影响因素）与输出变量（调剖效果）之间的非线性关系，最终将二者的复杂关系转化为非线性函数估计和逼近的数学求解问题。

1　最小二乘支持向量机算法

1.1结构风险最小化原理

设某区域的样本为n维向量，则该区域的m个样本及其值可表示为：

传统机器学习方法采用经验风险最小化原则，即最小化：

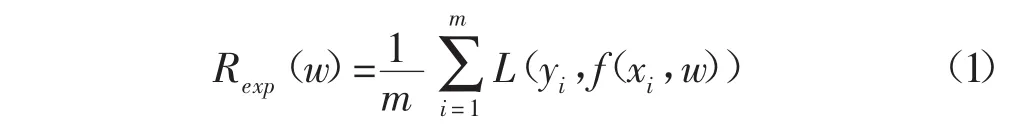
根据Vapnik结构风险最小化原则，机器学习的最终目的是最小化期望风险，即最小化：

上式中：R（w）-风险函数；f（x，w）-预测函数集，是对变量x和y之间关系的估计；L（y，f（x，w））-采用f（x ，w）对y进行预测产生的损失函数；F（x，y）-变量x和y的联合分布概率。根据概率与数理统计理论，经验风险最小不等于期望风险最小，二者在极坏分布情况下，以概率1-η满足以下关系：

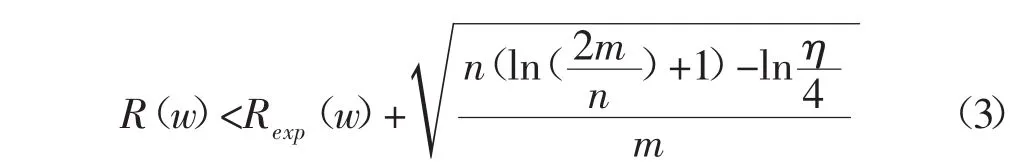
1.2最小二乘支持向量机

SVM是结构风险最小化理论的实现，由Vapnik等于1995年首先提出[8]。SVM因其较好的泛化能力用来解决各领域中的高维非线性映射问题。LSSVM是标准支持向量机的一种扩展，它采用最小二乘线性系统作为损失函数，将求解二次规划问题转化为求解一组线性方程。对于n维向量、m个样本，通过非线性变换z=φ（xi），将n维向量映射到l（l＞＞n）维这个高维度特征空间中，利用SVM算法实现输入数据与输出数据之间的非线性拟合，并允许出现拟合偏差。其数学关系表现形式为：

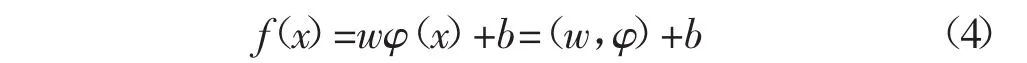
式中：w-权值矢量；φ（x）-非线性映射，生产和输入向量x同维的向量；b-偏差；（w，φ）-w和φ（x）的点积。

LSSVM最优化问题是寻找一个函数，在规定误差内能够估计出几乎接近目标的输出，同时最小化w模型参数，使其具有更强的泛化能力，使回归模型在模型推广能力和经验风险之间找到最佳平衡点，即结构风险最小化。对于最小二乘支持向量机方法，优化目标等价于一个最基本的凸二次规划问题，其形式如下：

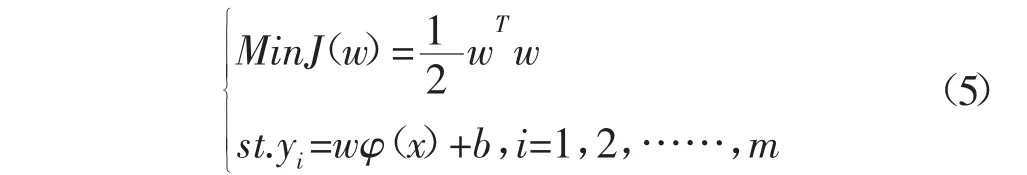
在LSSVM回归模型容许的拟合误差范围内，引入松弛系数ξ，带有松弛系数的同等最优化问题可表示为：

式中：J（w，ξ）-误差控制函数；ξ-松弛系数，用于表征允许拟合误差的程度；wTw-控制模型的复杂度；C-惩罚因子，用于控制训练错误率与泛化能力的一个折中系数，用来惩罚超出误差的数据点，并作为误差与优化目标之间的权重。

利用Lagrange乘数法求解式（6）的优化问题，转化为一个等价的二次规划问题，定义Lagrange函数：

式（7）中，αi（i=1，2，…，m）为Lagrange乘子。

根据KKT优化条件得到：

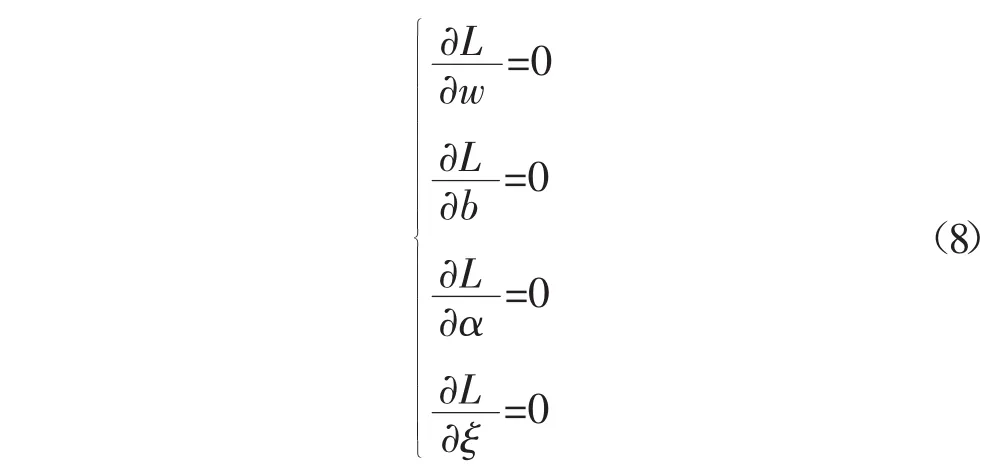
则有：

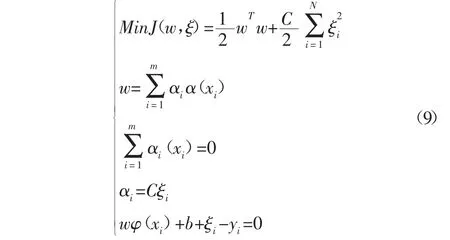
引入核函数，K（xi，yi）=φ（xi）·φ（yi），根据式（9），将求解优化问题转化为求解线性方程：

解上述线性方程组可得到Lagrange乘子αi和偏差参数b，由此确定LSSVM的输出为：

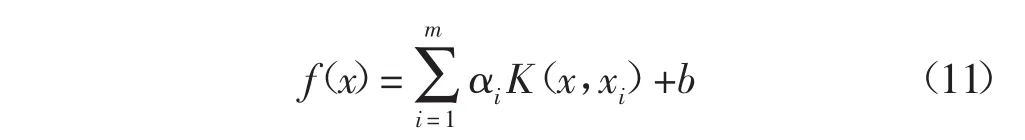
式（11）即为需要的LSSVM模型。式中函数f（x）完全由αi乘子决定。根据LSSVM回归函数的性质，只有少数的αi不为0，这些参数对应的向量称之为支持向量，偏差b也可以由标准支持向量计算得到。由于式（11）描述的对象是一个凸规划问题，其任一解均为全局最优解，而无局部极值问题，即具有较强的全局搜索能力[14]。

另外，式中的核函数是一个必须满足Mercer条件的函数。核函数有很多形式，本文采用能够较好解决复杂非线性问题的径向基RBF核函数，其表达式为：

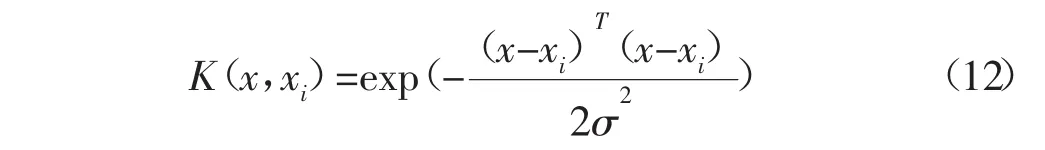
式中：σ-核宽度。最终得到支持向量回归机的估计函数：

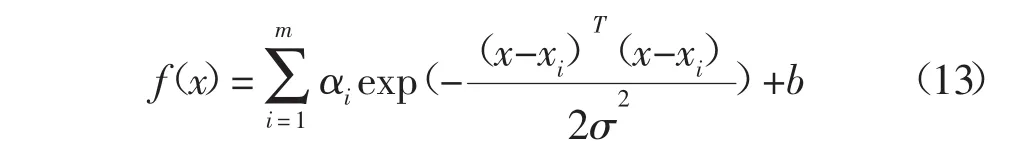
2　模型属性参数确定

2.1输入参数选取及归一化

调剖效果作为输出参数是确定的，但其影响因素较多，且各因素对调剖效果好坏的关联程度各不相同，这些因素还可能相互关联。本文用灰色关联法确定调剖效果的主控因素。首先将各因素属性值进行归一化处理，具体为采用线性函数法中的最大最小值法将各因素属性值都映射到［0，1］区间。对于某一特定的属性序列xi（i=1，2，…，m），则有：

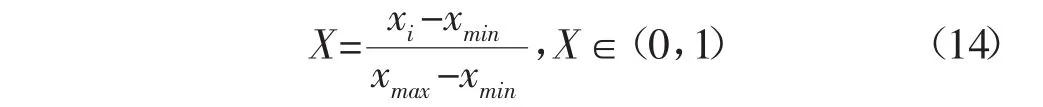
式中：x、X分别为归一化前后的因素属性值；xmax、xmin分别为因素属性的最大值和最小值。根据结果对影响调剖效果的系列因素进行关联度排序，选择影响调剖效果的主控因素作为模型的输入参数。此外，在模型进行样本训练时，同样使用归一化的属性值，以利于提升核函数点积计算速度。

2.2核函数参数优化

实践表明，合理确定LSSVM模型的松弛系数ξ、惩罚因子C、核函数RBF的基宽σ，可以显著提升模型的精度和推广能力。本文采用交叉验证网格搜索方法来确定松弛系数ξ、惩罚因子C和核宽度σ，并将其最优参数组合代入RBF核函数，通过公式（13）即可得到需要的LSSVM模型。

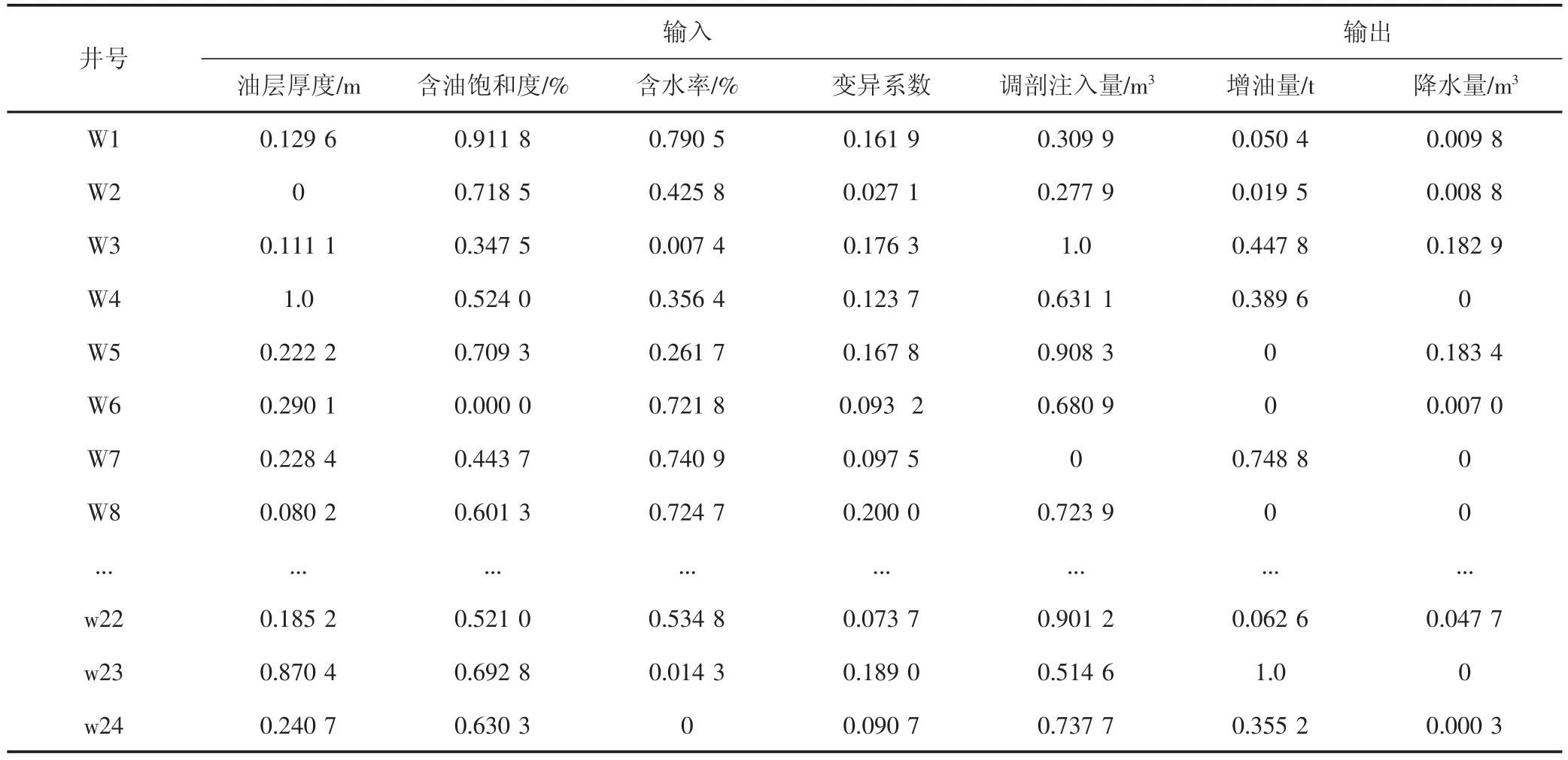
表1　LSSVM归一化训练样本Tab.1 Normalized training sample of LSSVM

3　矿场实例应用

靖安油田五里湾区块为典型的低渗透油藏，储层平均孔隙度12.74 %，平均渗透率1.81×10-3μm2，有效厚度12.4 m。区块于1998年大规模投产，采用300 m× 300 m近似正方形反九点井网、同步注水开发。开发过程中含水不断上升，2014年底综合含水达51.7 %，表现出含水加快上升，产量下降，平面及纵向矛盾日益突出。2015年以来，通过开展“弱凝胶+凝胶颗粒”深部调剖技术应用，有效缓解了油藏水驱不均矛盾，稳油控水效果明显。

以五里湾区块2015年实施的24口调剖井组为例，首先将众因素属性值归一化，通过灰色关联法得到与调剖效果关联度前五位的油层厚度、含油饱和度、含水率、变异系数和调剖注入量作为模型的输入参数，目标输出分别为调剖井组增油量和降水量。将上述输入输出参数归一化后作为学习样本（见表1），应用LSSVM进行该区调剖效果的训练与回归。在初始训练样本确定的情况下,利用交叉验证网格搜索方法得到松弛系数ξ=0.01、惩罚因子C=400、基宽σ=2，使得最终LSSVM法计算结果是唯一的。将24个训练样本进行预处理后用于LSSVM学习。利用LSSVM进行训练得到的增油量、降水量计算值与真实值的相关系数R2分别为0.988 4、0.845 6，拟合程度较高，说明该预测模型可靠性较好（见图1）。

利用训练好的预测模型对五里湾区块未参与学习的3口调剖井进行预测及对比。结果表明（见表2），模型预测的井组增油量与实际值的平均相对误差为5.71 %，井组降水量与实际的平均相对误差为2.71 %，能够满足矿场应用的精度要求。

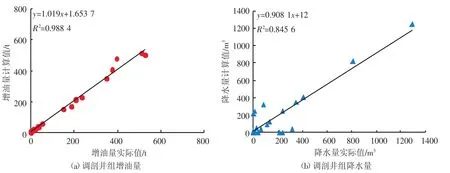
图1　训练样本计算值与实际值的对比Fig.1 Comparison between calculated and actual values for training sample

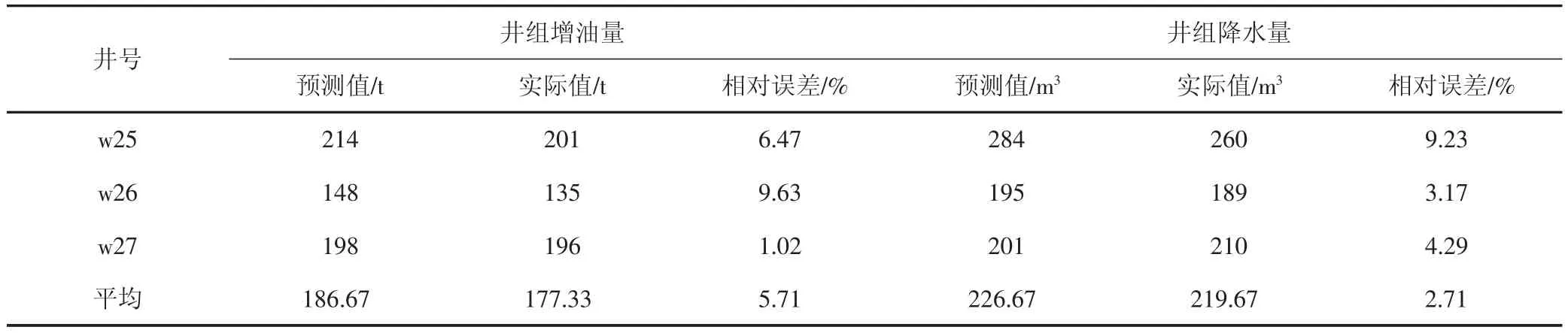
表2　检验样本的实际值与模型预测值对比Tab.2 Comparison between calculated and actual values for inspection sample

4　结论及认识

（1）调剖效果受多因素影响，难以将其与各影响因素之间建立一种确定的数学关系用于矿场应用计算。利用在小样本条件下解决关联属性之间的多维非线性问题的优越性，提出采用最小二乘支持向量机法建立调剖效果与其主控因素之间的非线性映射数学模型，进而预测未知井的调剖效果。

（2）以靖安油田五里湾区块调剖井为学习样本，将调剖后井组增油量和降水量作为目标输出，进行了最小二乘支持向量机法实例计算及验证。计算结果与样本实际值拟合相关性较高，预测相对误差在6 %以内，该方法用于调剖效果预测及评价是可行的。

参考文献：

［1］赵明宸，陈月明，蒋海岩，等.调剖措施效果影响因素的不确定性及其关联分析［J］.中国石油大学学报（自然科学版），2006，30（6）：59-62.

［2］徐耀东，任允鹏，丁良成，等.基于支持向量机的调剖效果预测方法研究［J］.断块油气田，2007，14（2）：50-52.

［3］巫祥阳，等.基于支持向量机的调剖措施效果预测模型研究［J］.石油天然气学报，2006，28（5）：120-121.

［4］汪洪，乔方，于春涛.影响调剖效果因素的分析［J］.钻采工艺，2008，31（增刊）：65-67.

［5］姜汉桥，刘伟，袁谋，等.多轮次调剖数值模拟研究［J］.石油钻采工艺，2003，25（5）：63-66.

［6］李梅，康志江.深度调剖数值模拟研究与应用［J］.大庆石油地质与开发，2004，23（3）:76-77.

［7］王清平.化学调剖效果经济评价方法研究［D］.浙江：浙江大学，2002.

［8］Vapnik V N.The nature of statistical learning theory［M］.NewYork:Springer，1995.

［9］张学工.关于统计学习理论与支持向量机［J］.自动化学报，2000，26（1）:32-41.

［10］杨位民，田芳，龚声蓉，等.基于支持向量机的压裂井层优选［J］.计算机工程，2006，32（7）:247-249.

［11］聂玲玲，童凯军，侯东梅，等.利用支持向量机方法求取缝洞型油气藏地层系数［J］.中国海上油气，2011，23（2）:93-96.

［12］侯健，乐友喜，王才经，等.基于统计学习理论的提高采收率潜力预测［J］.石油大学学报（自然科学版），2004，28（4）：67-70.

［13］钱晓山，阳春华.基于GEP的最小二乘支持向量机模型参数选择［J］.智能系统学报，2012，7（3）:1-5.

［14］Xu Kaikuo，et al.A novel method for real parameter optimization based on gene expression programming［J］.Applied Soft Computing，2009，9（2）:725-737.

Effect prediction of profile control based on least squares support vector machine in low permeability reservoir

ZHAO Yanhong1，MA Siju2，LIU Xiaoping2，JING Wenjie2，ZHANG Zhaozhao2
（1.Research Institute of Xi'an Changqing Chemical Group Co.，Ltd.，Xi'an Shanxi 710018，China；2.Oil Production Plant 3 of PetroChina Changqing Oilfield Company，Yinchuan Ningxia 750006，China）

Abstract:The efficiency of profile control is influenced by many factors such as geological conditions,development status and profile control technology,and effect prediction of profile control is considered as solving a complicated nonlinear problem which is influenced by many factors.It can not meet the actual application needs for conventional numerical simulation method with the demanding accuracy of geological modeling and the long time of history fitting.The least squares support vector machine（LSSVM）was used to construct the nonlinear mapping model between the profile control effect and its main controlling factors in this paper,and effect prediction of profile control for unknown well is transformed to the process of solving a nonlinear function.Based on the data of 24 profile control wells of Wuliwan block in Jing'an oilfield,the LSSVM forecast model of increasing oil and decreasing waterbook=38,ebook=43was established,and it was verified by inspection sample.The results show that the fitting accuracy between calculation results and actual values is relatively high and the error is small, the method can be used for prediction and evaluation of profile control effect in field.

Key words：efficiency of profile control；influence factors；least squares support vector machine；prediction model；Wuliwan block

*收稿日期：2015－12-31

DOI:10.3969/j.issn.1673-5285.2016.03.010

中图分类号：TE348

文献标识码：A

文章编号：1673-5285（2016）03-0037-05