基于范数正则化矩阵补全的无线传感网定位算法

肖　甫　沙朝恒　陈　蕾,2　孙力娟　王汝传

1(南京邮电大学计算机学院　南京　210003)

2(江苏省无线传感网高技术研究重点实验室(南京邮电大学)　南京　210003)

3　　　(宽带无线通信与传感网技术教育部重点实验室(南京邮电大学)　南京　210003)

(xiaof@njupt.edu.cn)



基于范数正则化矩阵补全的无线传感网定位算法

肖甫1,2,3沙朝恒1陈蕾1,2孙力娟1,2,3王汝传1,2,3

1(南京邮电大学计算机学院南京210003)

2(江苏省无线传感网高技术研究重点实验室(南京邮电大学)南京210003)

3(宽带无线通信与传感网技术教育部重点实验室(南京邮电大学)南京210003)

(xiaof@njupt.edu.cn)

Localization Algorithm for Wireless Sensor Networks via Norm Regularized Matrix Completion

Xiao Fu1,2,3, Sha Chaoheng1, Chen Lei1,2, Sun Lijuan1,2,3, and Wang Ruchuan1,2,3

1(SchoolofComputerScienceandTechnology,NanjingUniversityofPostsandTelecommunications,Nanjing210003)2(JiangsuHighTechnologyResearchKeyLaboratoryforWirelessSensorNetworks(NanjingUniversityofPostsandTelecommunications),Nanjing210003)3(KeyLaboratoryofBroadbandWirelessCommunicationandSensorNetworkTechnology(NanjingUniversityofPostsandTelecommunications),MinistryofEducation,Nanjing210003)

AbstractLocalization is one of the important preconditions for wireless sensor networks (WSNs) applications.Traditional range-based localization algorithms need large amounts of pair-wise distance measurements between sensor nodes.However, noise and data missing are inevitable in distance ranging, which may degrade localization accuracy drastically. To address this challenge, a novel localization algorithm for WSNs based on L1-norm regularized matrix completion (L1NRMC) is proposed in this paper. By utilizing the natural low rank feature of the Euclidean distance matrix (EDM) between nodes, the recovery of partly sampled noisy distance matrix is formulated as an L1-norm regularized matrix completion problem, which is solved by alternating direction method of multipliers (ADMM) and operator splitting technology.Based on the reconstructed EDM, the classical MDS-MAP algorithm is applied to obtain the coordinates of all the unknown nodes.This algorithm can not only detect and remove outliers, but also smooth the common Gaussian noise implicitly. Simulation results demonstrate that compared with traditional node localization algorithms, our algorithm achieves high accuracy from only small fraction of distance measurements and resists various types of ranging noise, which makes our algorithm suitable for resource-limited WSNs.

Key wordswireless sensor networks (WSNs); localization; outlier; matrix completion; L1-norm regularization

摘要节点定位是实现无线传感器网络(wireless sensor networks, WSNs)应用的重要前提之一.针对传统基于测距的定位方法需要大量节点距离信息以及多径效应、噪声干扰等导致的节点测距误差问题，提出了一类基于L1范数正则化矩阵补全(L1-norm regularized matrix completion, L1NRMC)的WSNs节点定位方法.该方法基于传感网节点间距离矩阵低秩特性，将部分采样信息下的距离恢复问题建模为稀疏野值噪声(outlier)情形下的矩阵补全问题，然后采用交替方向乘子法(alternating direction method of multipliers, ADMM)结合算子分裂技术(operator splitting technology)对该问题进行求解，所设计的非精确L1范数正则化矩阵补全(InExact-L1NRMC)算法不仅能显式解析采样矩阵中的稀疏野值噪声，也可隐式平滑常见的高斯随机噪声.仿真结果表明:相比已有的同类定位方法，该算法只需进行部分测距采样即可实现精准的节点定位，且对各类测距噪声具有很好的抗干扰能力，适用于资源受限的WSNs.

关键词无线传感器网络;定位;野值噪声;矩阵补全;L1范数正则化

近年来，无线传感器网络(wireless sensor networks, WSNs)技术得到快速发展，其正广泛应用于军事侦查、智能交通、环境监测等领域[1]，智能家居系统、自动泊车距离警告、森林火险监控等均为WSNs的典型应用.在WSNs中，节点自身位置信息的获取对各种应用至关重要.受限于节点能量、部署条件和经济因素等， 一般WSNs只有少数锚节点通过装载GPS等获取自身位置，其他未知节点的位置信息则由定位算法计算得到.目前已有许多解决WSNs自定位的方案[2]， 如凸规划算法、DV-hop算法[3]、MSVR算法[4]等.整体上传感器网络节点定位可分为基于测距的定位算法和与测距无关的定位算法2大类，前者可实现较为精确的定位，但计算和通信开销较大，且需要一定的硬件支持;后者定位精度较低，但计算开销较小，适用于低功耗、低成本的应用领域.

本文侧重研究基于测距的WSNs节点定位算法，该类定位算法一般可描述为：已知WSNs中少量节点，即锚节点的位置信息，通过测距获得部分或全部节点之间的距离数据，据此求解未知节点的位置信息.常见的测距定位算法包括：多点定位、半定规划(semi-definite programming, SDP)算法[5-6]和MDS-MAP(multidimensional scaling and MAP)[7-8]算法等.一般情况下，这些算法均需获知大部分距离数据且要求距离数据较为精确，否则将导致较大的定位误差.然而，实际情况中受限于无线传感器节点自身的能量，往往无法获取足够的距离数据[9];此外受噪声因素的影响，采样的距离数据也不可避免地存在误差.已有研究工作[10-12]表明：在节点距离数据采样中，除了常见的高斯噪声，受节点硬件故障、非视距传播、环境干扰及恶意攻击等因素的影响，采样的节点距离数据中往往还包括部分远超正常范围的异常值噪声干扰，本文将其称为野值噪声(outlier)，这类噪声严重影响了传感器节点的定位精度.

针对上述问题，本文提出了一种基于L1范数正则化矩阵补全(L1-norm regularized matrix com-pletion, L1NRMC)的WSNs定位算法.通过将无线传感器节点之间的距离数据构造成平方欧氏距离矩阵(Euclidean distance matrix, EDM)，矩阵中只包含采样获得的少量距离元素，且这些元素可能含有噪声.由于节点间的平方距离矩阵具有低秩特性，采用扩展的矩阵补全方法，综合考虑野值噪声和高斯噪声，通过引入L1范数正则化因子对野值噪声进行平滑，将噪声下的矩阵补全建模为凸优化问题，在此基础上通过交替方向乘子法(alternating direction method of multipliers, ADMM)[13]结合算子分裂技术(operator splitting technology)[14]进行求解以补全和恢复距离矩阵，在此基础上求解待定位节点的位置信息.

1相关工作

基于测距的WSNs节点定位算法一般包括2个步骤：1)利用某种测距方法测量节点之间的距离;2)利用测得的距离数据结合锚节点坐标信息计算未知节点坐标.典型的测距方法主要包括：基于信号传输时间(time of arrival, TOA)的方法、基于信号传输时间差(time difference of arrival, TDOA)的方法以及基于信号接收信号强度(received signal strength indicator, RSSI)的方法.这3种测距方法各具优势，但均易受多路径反射、非视距问题及环境干扰等因素影响，从而导致较大的测距误差.

文献[5-6]将WSNs节点定位问题看作欧几里得矩阵补全问题和图实现问题的一个变形，以测距获得的距离数据为约束，通过引入松弛变量把非凸二次距离约束转化为线性约束，将WSNs定位问题建模为半定规划问题，从而获得最优的定位结果;文献[15]利用网络拓扑结构的局部信息，提出了一种局部保持的典型相关分析模型来建立从信号空间到现实物理空间的映射，以获得更高的定位精度;文献[7-8]引入经典的多维尺度(multidimensional scaling, MDS) 数据分析方法，将无线传感器节点间的距离关系映射至低维空间，基于最短路径求解节点间的近似距离，产生一个最符合节点间距离关系的相对坐标地图，并利用少量锚节点的位置信息将相对位置转换为全局位置.然而，上述算法均需精确地获取节点间的距离数据或基于最短路径算法构造节点距离矩阵，对采样数量和采样精度均有较高要求，且在网络拓扑不规则时定位精度不高.但在实际的WSNs应用中，可能只能获取部分距离数据，并且这些数据往往存在误差;此外从节能的角度，需尽可能减少节点间的测距信号传输.因此，对采样的距离数据进行修正和补全对于节点的精确定位具有重要意义.文献[10]基于图刚性理论，通过定义可检验边来进行野值噪声的检测，实现节点间距离数据的修正，从而提高节点定位的精度;文献[11]提出了一种野值鲁棒的WSNs定位算法，在多点定位的基础上引入鲁棒的区域合并操作，有效消除野值噪声以修正采样距离数据;文献[12]则将节点定位视为一种图嵌入问题，利用冗余刚性理论来检测和去除距离数据中的野值噪声，从而获得更高的定位精度.但上述工作主要关注通过降低野值噪声对距离数据进行修正，从而实现精确的节点定位，其均没有考虑节点距离矩阵的补全操作.事实上，节点的距离矩阵具有低秩特性，可采用矩阵补全算法[16]基于部分数据采样实现距离矩阵的较为精确恢复.常见的矩阵补全算法包括奇异值阈值(singular value thresholding, SVT)算法[17]、OptSpace算法[18]、FPCA算法[19]等，当矩阵采样元素无噪或仅包含高斯噪声时，这些算法均能较精确地恢复原矩阵[20]，但对于野值噪声则效果不够理想.文献[9]综合考虑了距离矩阵的修正和补全，采用秩最小化原理约束采样距离矩阵，在此基础上提出了一种新型的基于SVT的WSNs节点定位算法，但其只是将距离数据包含的噪声简单地假设为单纯的高斯随机噪声，忽略了因节点硬件故障、多径传输等导致的野值噪声的存在.事实上，少量的野值噪声会严重影响节点定位的精确性[10].针对文献[9]存在的问题，本文在距离矩阵补全的基础上引入L1范数正则化因子以处理野值噪声，研究并提出了一类基于L1NRMC的WSNs节点定位方法，从而进一步提高定位准确性.

2范数正则化矩阵补全算法

2.1相关数学基础

定义1. 矩阵奇异值分解(singular value decom-position, SVD)[21]. 设X是一个秩为r的n1×n2维矩阵，I是r×r维的单位矩阵，则存在2个正交矩阵：

U=(u1,u2,…,ur)∈n1×r，UTU=I，

V=(v1,v2,…,vr)∈n2×r，VTV=I，

以及对角阵Σ=diag({σi|1≤i≤r})且奇异值σ1≥σ2≥…≥σr>0，满足：

X=UΣVT，

(1)

式(1)称为矩阵X的奇异值分解.

定义2. 矩阵范数[21].设矩阵X∈n1×n2存在如式(1)所示的奇异值分解，则：

1) 矩阵X的L0范数定义为

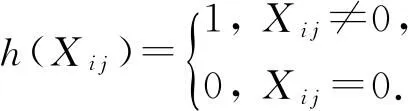
2) 矩阵X的L1范数定义为

3) 矩阵X的Frobenius范数定义为

定义3. 矩阵收缩算子[22]. 设矩阵X∈n1×n2，若τ≥0，则τ对应的矩阵收缩算子定义为

其中sgn(·)为符号函数.

定义4. 矩阵奇异值阈值算子[17].设矩阵X∈n1×n2存在如式(1)所示的奇异值分解，若τ≥0，则τ对应的奇异值阈值算子定义为Dτ(X)=USτ(Σ)VT.

定理1. 对任意的τ>0，Z∈n1×n2，矩阵收缩算子Sτ(Z)满足：

(2)

证明. 略，详见文献[22].

定理2. 对任意的τ>0，Z∈n1×n2，矩阵奇异值阈值算子Dτ(Z)满足：

(3)

证明. 略，详见文献[17].

定理3. 假设F1，F2是n1×n2上2个下半连续的凸函数，且F2在n1×n2中可微并具有β-Lipschitz连续梯度，则对于凸优化问题：

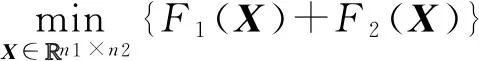
(4)

若函数F1+F2是强制的且严格凸的，则该问题存在唯一解，且对任意初始值X0及0<δ<2β，采用如下方法生成的迭代序列Xk+1是收敛到该问题的唯一解：

(5)

证明. 略，详见文献[14].

2.2L1NRMC算法

近年来，压缩感知理论[23]为信号采集技术带来了革命性的突破.众所周知，压缩感知理论要求在已知信号具有稀疏性的条件下对信号进行采集和重构，而在很多实际问题中，需要重构的目标常常是以矩阵的形式组织的.因此，压缩感知理论便自然地从向量空间被拓展至矩阵空间，从而利用矩阵奇异值向量的稀疏性，通过采样矩阵的部分元素来恢复低秩矩阵.在机器学习领域，这类问题通常被刻画为矩阵补全(matrix completion, MC)问题.迄今为止，矩阵补全理论已在图像修复[24]、三维运动估计[25]、无线传感网数据收集[26]、多标记图像分类[27]以及视频去噪[28]等领域得到了重要应用，也逐渐成为机器学习、模式识别以及计算机视觉领域中的主要研究热点之一.

自动化水平也是衡量钣金工艺先进性的重要标志之一。我国的钣金企业一般可以分为民营企业、国有企业两种类型，其中民营企业的占比大、数量大，但是缺乏资金与技术，在管理方面也存在许多漏洞。这样一来，导致市场上的大部分钣金工艺产品的质量得不到保障。除此之外，由于资金投入不足，这些企业的生产自动化水平达不到预期的标准，所以人员的劳动强度较高，劳动力成本占比过大，也不利于行业的平稳快速发展，带来了严重的滞后性问题。

标准的矩阵补全问题通常描述为

(6)

且Ω⊆[n1]×[n2]([n1]={1,2,…,n1}，[n2]={1,2,…,n2})为采样元素的下标集合，PΩ(·)为正交投影算子，表示当(i,j)∈Ω时，Mi j为采样元素，即：

(7)

由于矩阵的秩是一个非凸函数，该问题是一个NP-hard问题，求解该问题所需时间随着矩阵规模的增加成指数倍增长.受压缩感知理论的启发， Candès等人[16]引入矩阵的核范数来替代矩阵的秩函数， 并且Recht等人[29]还从理论上证明了矩阵秩函数可以被其凸包核范数所取代，因此式(6)可以松弛为

(8)

目前标准矩阵补全问题已有多种成熟的求解算法，如Cai等人[17]提出的SVT算法、Keshavan等人[18]提出的OptSpace算法、Ma等人[19]提出的不动点连续算法(fixed point continuation with approximate SVD, FPCA)及Toh等人[30]提出的加速近邻梯度算法(accelerated proximal gradient, APG)等.当矩阵采样元素无噪或仅包含高斯噪声时，这些算法均能精确地恢复目标矩阵.但当采样矩阵包含稀疏的野值噪声时，这些算法的性能将急剧下降.此处的野值噪声即异常值，通常指代那些远超正常范围的数据，这些数据往往意味着较大的误差.

为有效平滑此类野值噪声对矩阵补全性能的影响，本文将正则化技术引入到矩阵补全问题中.如何选取正则化因子通常由问题的具体要求决定.例如，为了得到压缩感知问题的稀疏向量解，压缩感知理论采用了向量L0范数来刻画其稀疏性，在目标函数中引入向量L0范数正则化因子.受此启发，我们将稀疏野值噪声情形下的矩阵补全问题建模为

(9)

由于矩阵的秩和L0范数均为非凸函数，式(9)是一个NP-hard问题.借鉴文献[31]的思想，我们将矩阵的秩函数松弛为矩阵核范数，将矩阵的L0范数松弛为L1范数，因此上述问题可松弛为如下凸优化问题：

(10)

进一步，由于实际应用中采样矩阵包含稀疏野值噪声的同时往往伴随着不同程度的高斯噪声，因此我们在设计式(10)的求解算法时不仅希望该算法能平滑野值噪声也能一定程度上平滑高斯噪声，为此我们引入优化领域流行的交替方向乘子法(ADMM)来求解该问题. 交替方向乘子法的实质是通过引入增广拉格朗日函数将约束优化问题转换为无约束优化问题，不妨设式(10)对应的增广拉格朗日函数为

(11)

则可以通过求解如下无约束优化问题来求得式(10)的最优解(X*,Y*,Z*)，即：

(12)

(13)

由交替方向乘子法易知，式(13)应按如下方式迭代求解：

(14)

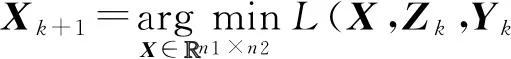
将式(11)代入子问题1后可得：

(15)

即：

(16)

进一步考察式(16),令:

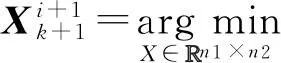
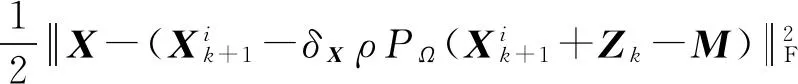
(17)

即：

(18)

进一步，由定理2可得：

(19)

将式(11)代入子问题2后可得：

(20)

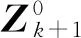
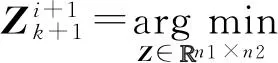
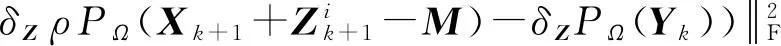
(21)

进一步由定理1可得：

(22)

因此，我们将式(10)的上述求解过程归纳为精确的L1范数正则化矩阵补全算法(exact L1-norm regularized matrix completion, Exact-L1NRMC)，算法1描述了Exact-L1NRMC算法的详细求解步骤.

算法1. Exact-L1NRMC算法.

输入：采样矩阵PΩ(M)、参数λ；

输出：目标矩阵Xopt、稀疏噪声矩阵Zopt.

① 初始化X0=0,Z0=0,Y0=0,k=0及kX，kZ；

② while 不收敛 do

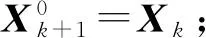
④fori=0 tokX

⑤

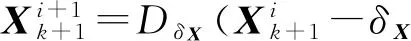
Zk-M)-δXPΩ(Yk));

⑥end for

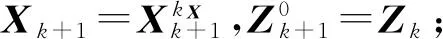
⑧ forj=0 tokZ

⑨

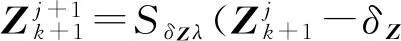
⑩end for

Zk+1=ZkZk+1;

事实上，我们并不需要求解出子问题的精确解，只需更新X与Z各一次得到子问题的一个近似解，就足以使算法最终收敛到原问题的最优解.据此，我们就可以得到一个更为简洁且收敛速度更快的算法，我们称之为非精确L1NRMC算法，算法2描述了非精确L1NRMC的求解步骤.

算法2. InExact-L1NRMC算法.

输入：采样矩阵PΩ(M)和参数λ；

输出：目标矩阵Xopt、稀疏噪声矩阵Zopt.

① 初始化X0=0,Z0=0,Y0=0,k=0；

② while 不收敛 do

③ Xk+1=DδX(Xk-δXρPΩ(Xk+Zk-M)-

δXPΩ(Yk));

④ Zk+1=SδZλ(Zk-δZρPΩ(Xk+1+Zk-M)-

δZPΩ(Yk));

⑤ Yk+1=Yk+ρPΩ(Xk+1+Zk+1-M);

⑥k=k+1;

⑦ end while

由算法2可以看出，InExact-L1NRMC算法在迭代过程中一方面可使变量Z和Y保持良好的稀疏性以节省存储空间，同时还能使变量X保持好的低秩性，而且算法的每一次迭代执行过程中只涉及一个SVD分解，这些特性确保了InExact-L1NRMC算法具有较高的时间和空间效率.

3基于矩阵补全的节点定位算法

节点定位技术是WSNs的重要支撑技术之一.准确地获取传感器节点的位置信息，可确保数据的有效性、提高路由效率、实现网络拓扑自适应配置等.在典型的WSNs应用中，大量的WSNs节点被随机部署在一个固定区域.通常情况下，如果能有效获取节点间完整的距离信息，那么将很容易根据锚节点的坐标计算得到未知节点的具体坐标.但由引言可知，我们能收集到的只是区域节点间的部分距离信息，而且这些距离信息往往还包含稀疏野值噪声和高斯随机噪声.

现有的矩阵补全算法在采样信息仅仅包含高斯随机噪声情形下效果良好，但无法有效处理稀疏野值噪声.本文提出的稀疏野值噪声情形下非精确L1范数正则化矩阵补全 (InExact-L1NRMC) 算法(即算法2)不仅能显式处理稀疏野值噪声，还能通过拉格朗日参数ρ的调节隐式平滑采样矩阵中的高斯随机噪声.因此，我们首先将基于部分采样信息的无线传感网节点间距离矩阵补全问题建模为如下的稀疏野值噪声情形下矩阵补全问题：

(23)

其中，PΩ(M)为含噪平方欧氏距离采样矩阵，N为稀疏野值噪声矩阵，D为待补全的平方欧氏距离目标矩阵.

事实上，矩阵补全理论适用的前提为目标矩阵为低秩或近似低秩.矩阵的秩为矩阵所包含的极大线性无关列向量或行向量的数目，低秩矩阵对应的秩远小于矩阵维度，即具有较高的冗余性，因此可以通过部分元素恢复出整个矩阵.为验证无线传感网节点间平方欧氏距离矩阵D的低秩性，我们采用如下引理和定理：

1) rank(A·B)≤min{rank(A),rank(B)};

2) rank(A+B)≤rank(A)+rank(B).

定理4. 假设xi∈d,i=1,2,…,n为d维空间中n个节点，如果记任意节点xi与xj之间的平方欧氏距离为Di j，则所得平方欧氏距离矩阵D的秩不超过d+2.

证明. 节点xi与xj之间的平方欧氏距离Di j可表示为

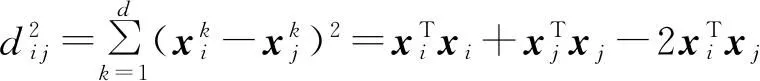
(24)

不妨令X=(x1,x2,…,xn)，B=XTX，1=(1,1,…,1)T表示单位n维列向量，则由式(24)可知：

(25)

其中diag(·)表示取矩阵主对角线元素的对应列向量.

由于rank(diag(B))=rank(1T)=rank(1)=1且rank(X)≤d，根据引理1可知：

rank(D)≤rank(diag(B)·1T)+rank(1·

[diag(B)]T)+rank(-2B)≤1+1+d=d+2，

即平方欧氏距离矩阵D的秩不超过d+2.

证毕.

由于传感网节点坐标一般为2维或者3维向量，根据定理4易知平方欧氏距离矩阵的秩一般不超过5.由秩的定义可知，评价矩阵低秩性好坏的依据是矩阵秩和矩阵维度的比值，该比值越小其低秩性越好.由于平方欧氏距离矩阵的秩不超过d+2，因此节点数量越多，则平方欧氏矩阵的维度越大，低秩性将越好，其冗余性也就越高，从而其补全性能也越好.此外，通过采用算法2，我们不仅可以精确补全节点间距离信息，而且可以显式解析出稀疏野值噪声矩阵，进而根据该矩阵精确定位出产生异常测距信息的节点对，从而为WSNs的节点故障诊断提供依据.

WSNs节点定位的最终目的是为了获得传感节点的具体坐标，经典的多维标度算法能有效利用完全距离矩阵信息准确估算整个网络中所有节点之间的相对位置.在获得了节点之间的相对位置信息后，本文进一步采用多维标度映射算法(MDS-MAP)根据锚节点的真实坐标及其对应相对坐标之间的关系，计算出将相对位置转换为绝对位置的坐标变换矩阵，从而将所有节点的相对坐标转换为绝对坐标.算法3给出了基于L1范数正则化矩阵补全的无线传感网节点定位算法的详细步骤.

算法3. 基于范数正则化矩阵补全的定位算法.

输入：部分含噪的距离信息PΩ(M)、坐标维度d及锚节点坐标T1,T2,T3；

输出：所有未知位置信息的节点坐标{Ti|i=4,5,…,n}.

① 基于算法2计算平方距离矩阵D：

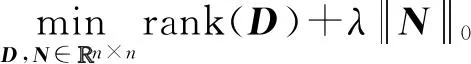
s.t.PΩ(M)=PΩ(D+N);

② 计算双中心化相似矩阵G：

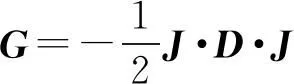
③ 对矩阵G进行SVD分解：

[U,Σ,V]=svd(G);

④ 计算相对坐标矩阵：

其中Ri∈d×1,Ud=U(∶,1∶d)；

⑤ 计算坐标变换矩阵：

Q=(T2-T1,T3-T1)·(R2-R1,R3-R1)-1;

⑥ 计算并输出所有节点坐标：

{Ti=Q·(Ri-R1)+T1,i=4,5,…,n}.

由算法3可知， 基于L1范数正则化矩阵补全的传感网节点定位算法主要由2部分组成，即“基于部分采样信息的距离矩阵补全”(依赖于算法2)和“基于完全距离矩阵的节点坐标计算”，因此其计算量主要体现在2次奇异值的分解上，对应时间复杂度为O(n3).为进一步提高算法的实时性，我们可以使用PROPACK[32]软件包进行部分奇异值分解，从而有效降低奇异值分解的时间复杂度.

4仿真实验

为验证算法性能，我们基于Matlab进行了仿真实验：在100 m×100 m的区域内随机部署100个无线传感器节点，其中4个节点为锚节点，其他节点为未知节点.令X∈2×n为节点的坐标矩阵，D∈n×n为节点间的平方距离矩阵(n为网络中节点个数，本实验中n=100).首先对矩阵D添加噪声干扰，得到含噪距离矩阵Dnoise;然后从Dnoise中随机采样部分元素作为已知的采样距离数据，使用本文提出的算法2对采样矩阵进行恢复;最后，利用算法3求解所有待定位节点的具体坐标.我们选取如下2个指标来衡量算法性能：

1) 距离矩阵补全误差

(26)

其中,D′为补全后的距离矩阵.ec衡量了补全后的距离矩阵与原始真实距离矩阵的相对误差，其值越小，表明距离矩阵补全效果越好.

2) 传感器节点定位误差

(27)

其中,X′表示算法3计算得到的坐标矩阵.el衡量了定位算法计算得到的节点坐标与其真实坐标间的绝对误差，其值越小，表明定位效果越好.

为考察算法在不同噪声污染情形下的性能，我们设计了4组不同的实验.实验1～4分别考察在无噪声条件、野值噪声、高斯噪声及高斯野值混合噪声条件下的算法效果.4组实验均以文献[18]所研究的基于OptSpace算法的矩阵补全及文献[8]研究的基于SVT算法补全的WSNs节点定位算法进行对比.

实验1. 无噪声实验

本实验假设所有距离数据均为准确值，不包含任何噪声.图1显示了对距离矩阵进行不同比例采样情况下的距离矩阵补全误差及传感器节点定位误差的变化情况.横轴代表距离矩阵采样比例，图1(a)中纵轴代表距离矩阵补全误差，图1(b)中纵轴则代表传感器节点定位误差.

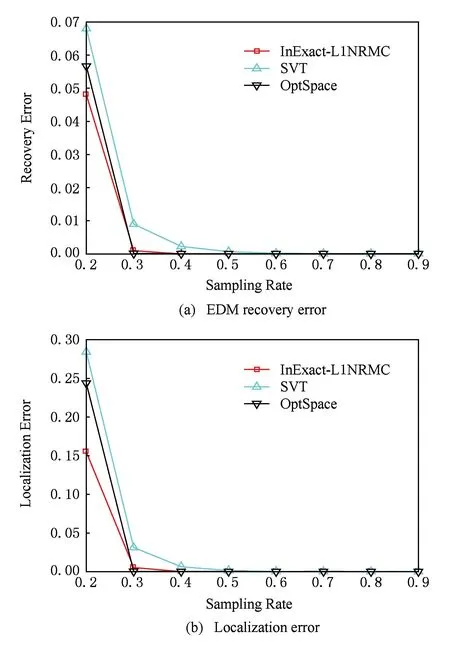
Fig. 1　Relationship between error and sampling rate without noise.图1　无噪声条件下误差与采样比例的关系

由图1(a)可以看出，无噪声条件下本文算法2的矩阵补全精度优于SVT算法和OptSpace算法，只需采样20%的距离数据即可得到低于0.05的补全误差.对比图1(a)与图1(b)可知，传感器节点定位误差与距离矩阵补全误差是一致的， 算法2对应的节点定位误差同样小于SVT算法和OptSpace算法，具体在20%的采样率条件下， 算法2对应的节点定位误差约为0.15 m.

实验2. 野值噪声实验

本实验假设采样数据仅包含野值噪声,实验中野值噪声大小由5 000～10 000 m之间随机产生.对于算法2，野值噪声比例(sparse ratio)分别设定为1%，5%，10%这3种；SVT算法和OptSpace算法则设定为5%.图2显示了在对距离矩阵进行不同比例采样情况下误差的变化情况.

Fig. 2　Relationship between error and sampling rate under the condition of sparse outlier.图2　野值噪声条件下误差与采样比例的关系

由图2(a)可以看到，SVT算法和OptSpace算法在野值噪声条件下效果较差，即使当距离数据采样比例接近于1时补全误差仍在0.15以上，这说明SVT算法和OptSpace算法无法处理野值噪声;对于本文提出的算法2，在不同比例的野值噪声条件下，当距离数据采样比例超过30%时，距离矩阵补全误差均接近于0.对比图2(a)与图2(b)，传感器节点定位误差与距离矩阵补全误差是一致的.SVT算法和OptSpace算法对应的定位误差较大，一般都在1 m以上;而对于本文算法2，随着采样比例的增加，定位误差迅速降低，当距离数据采样比例达到30%时即可实现接近于0的定位误差.具体到30%的采样率，在1%，5%，10%这3种野值噪声条件下，本文算法2对应的定位误差在0～0.2 m之间，野值噪声越稀疏，则定位误差越小.

同时，在实验过程中发现，当采样的距离数据到达一定比例时，本文算法2能够较准确地预测野值噪声元素所在位置，这有助于了解无线传感器节点所处的环境及其自身状态，进而为WSNs节点故障诊断、调度策略及拓扑调整等提供依据.

定义野值噪声识别率pr为

(28)

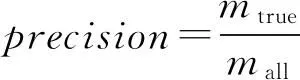
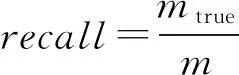
其中,mall表示算法2识别的野值噪声元素个数，mtrue表示所识别的野值噪声元素中的确为野值噪声元素的个数，m表示采样元素中包含野值噪声的元素个数.

如图3所示，随着距离数据采样比例的增大，野值噪声识别率逐步提高;当采样比例为40%时，稀疏噪声元素识别率接近于1，此时绝大部分野值噪声位置都可准确预测.

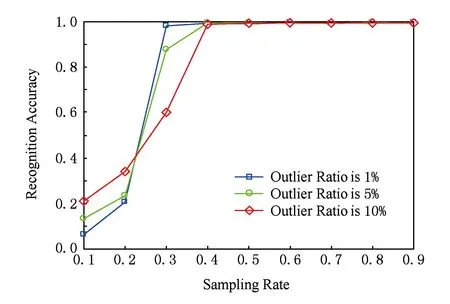
Fig. 3　Relationship between recognition accuracy and sampling ratio under the condition of sparse outlier.图3　野值噪声识别率与采样比例的关系

实验3. 高斯噪声实验

本实验假设距离数据仅包含高斯噪声.实验中高斯噪声均值为0，标准差为100.图4显示了对距离矩阵进行不同比例采样情况下误差的变化情况.

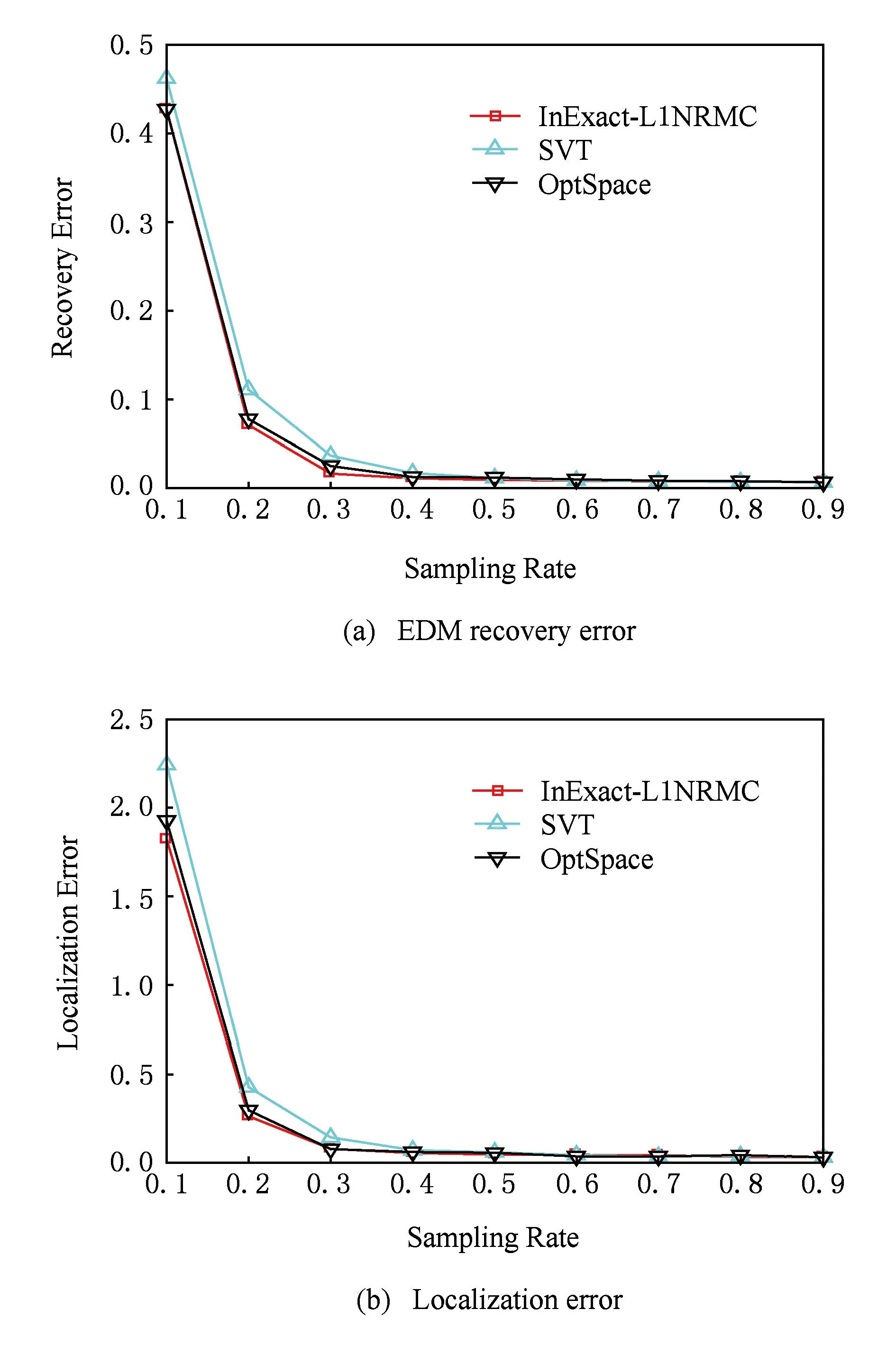
Fig. 4　Relationship between error and sampling rate under the condition of Gaussian noise.图4　高斯噪声条件下误差与采样比例的关系

由图4可以看出，本文提出的算法2和传统SVT算法、OptSpace算法均能有效地处理高斯噪声；算法2的矩阵补全精度优于SVT算法，但与OptSpace算法相当;算法2对应传感器节点定位误差略低于SVT算法，但与OptSpace算法相当.当采样比例达到30%时3种算法的定位误差均接近0.

实验4. 混合噪声实验

本实验中我们同时考虑野值噪声与高斯噪声的影响.实验中野值噪声大小由5 000～10 000之间随机产生，高斯噪声均值设置为0，标准差设置为100;和实验2类似，对于算法2，噪声比例分别设定为1%，5%和10%，SVT算法和OptSpace算法则设定为5%.实验结果如图5所示.

如图5所示，SVT算法和OptSpace算法在混合噪声条件下误差较大，无法实现节点的精确定位;与单一噪声条件相比，算法2在混合噪声条件下的距离矩阵补全误差以及节点定位误差在整体上均有一定幅度的增加，但当距离数据采样比例高于30%时，补全误差和定位误差均大幅减小并趋于稳定，此时算法仍能实现较高的定位精度.具体到30%的采样率，在1%，5%，10%这3种野值噪声条件下，算法2对应的定位误差在0～0.35 m之间，野值噪声越稀疏，对应定位误差越小，当野值噪声比例为1%时，定位误差低于0.12 m.

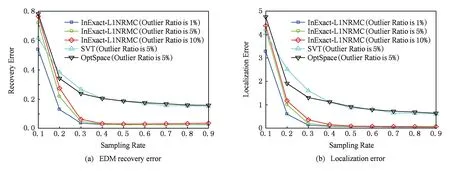
Fig. 5　Relationship between error and sampling rate under the condition of mixed noise.图5　混合噪声条件下误差与采样比例的关系

图6显示了100个传感器节点的最终定位结果.实心正方形代表锚节点，它们和未知节点一样随机部署在100 m×100 m的区域内;实心点对应未知节点的实际位置；空心圆则代表采用本文算法3计算得到的节点位置.图6(a)中距离数据采样率设定为30%，野值噪声比例设定为10%，无高斯噪声;图6(b)中距离数据采样率设定为30%，野值噪声比例设定为1%，高斯噪声均值为0，标准差为100.从图6可见，空心圆和实心点实现了较好的对应及吻合，验证了在含噪的部分采样距离条件下，本文算法2可较准确地实现传感器节点定位.

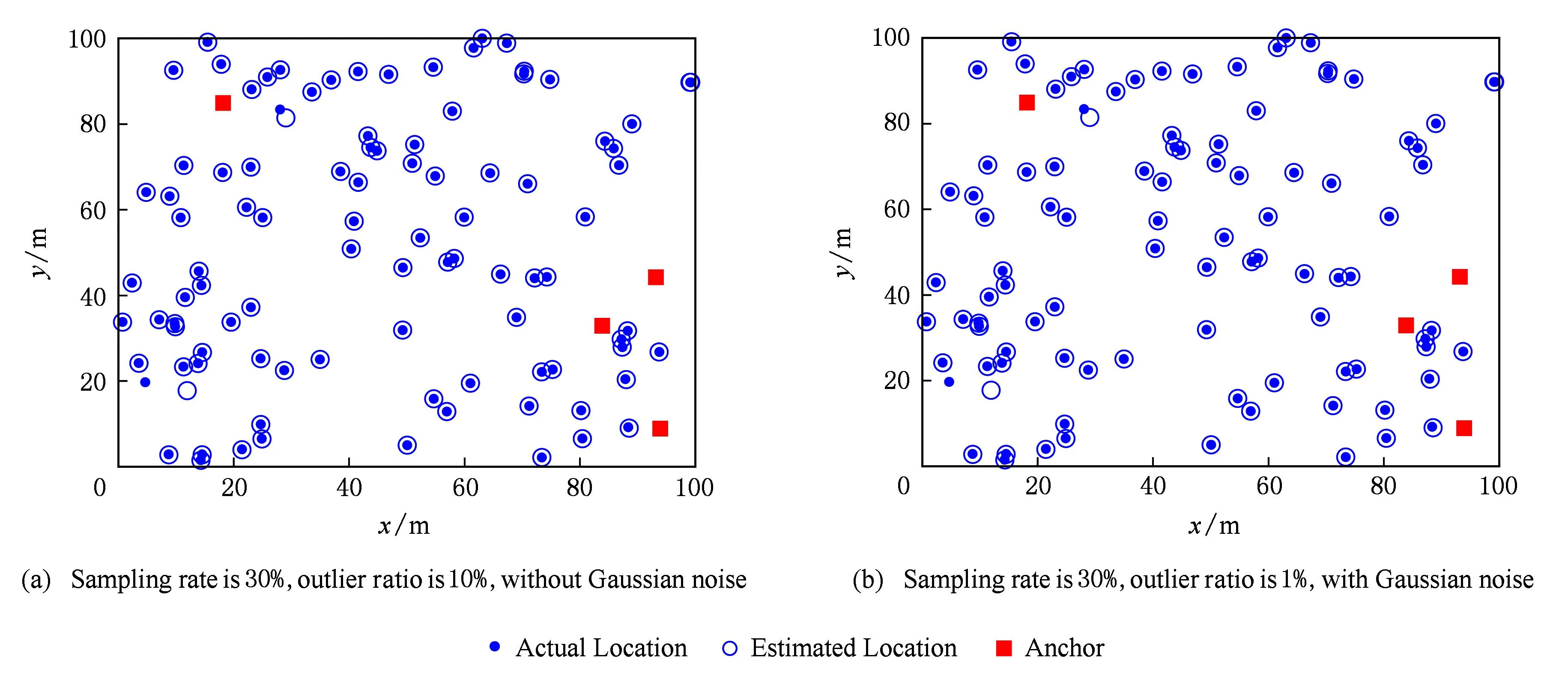
Fig. 6　Localization results under the condition of different sampling rates and different noise ratios.图6　不同采样率和噪声比例下的节点定位结果图

5结论

本文基于WSNs节点距离矩阵低秩特性，提出了一种基于矩阵补全的节点定位算法.传统矩阵补全算法只适用于无噪声或高斯随机噪声，而WSNs中节点间的无线通信受多径效应、非视距传播、硬件故障、恶意攻击等因素导致测距往往还包含野值噪声，其严重影响节点定位精度.因此本文基于节点间距离矩阵低秩特性，将部分采样信息下的距离恢复问题建模为稀疏野值噪声情形下的矩阵补全问题，在此基础上采用交替方向乘子法结合算子分裂技术进行求解.仿真结果表明，本文算法只需进行少量节点测距即可实现精准的定位，且在无噪声条件下、高斯噪声条件下、野值噪声条件下和高斯野值混合噪声条件下均能获得较高的定位精度.此外，算法还可较为准确地预测野值噪声所在位置，从而为WSNs节点故障诊断提供依据.

参考文献

[1]Akyildiz I F, Su Weilian, Sankarasubramaniam Y, et al. A survey on sensor networks[J]. IEEE Communications Magazine, 2002, 40(8): 102-114

[2]Han Guangjie, Xu Huihui, Duong T Q, et al. Localization algorithms of wireless sensor networks: A survey[J]. Telecommunication Systems, 2013, 52(4): 2419-2436

[3]Wang Yun, Wang Xiaodong, Wang Demin, et al. Range-free localization using expected hop progress in wireless sensor networks[J]. IEEE Trans on Parallel and Distributed Systems, 2009, 20(10): 1540-1552

[4]Lee J, Choi B, Kim E. Novel range-free localization based on multidimensional support vector regression trained in the primal space[J]. IEEE Trans on Neural Networks and Learning Systems, 2013, 24(7): 1099-1113

[5]So M, Ye Yinyu. Theory of semi-definite programming for sensor network localization[J]. Mathematical Programming, 2007, 109(23): 367-384

[6]Shamsi D, Taheri N, Zhu Zhisu, et al. Conditions for Correct Sensor Network Localization Using SDP Relaxation[M]. Berlin: Springer, 2013

[7]Shang Yi, Zhang Ying, Ruml W, et al. Localization from mere connectivity[C]Proc of the ACM Int Symp on Mobile Ad Hoc Networking and Computing (MobiHoc). New York: ACM, 2003: 201-212

[8]Sun Xiaoling, Chen Tao, Li Weiqing, et al. Performance research of improved MDS-MAP algorithm in wireless sensor networks localization[C]Proc of the IEEE Int Conf on Computer Science and Electronics Engineering. Piscataway, NJ: IEEE, 2012: 587-590

[9]Feng Chen, Valaee S, Au W S A, et al. Localization of wireless sensors via nuclear norm for rank minimization[C]Proc of the 53rd IEEE Global Telecommunications (GLOBECOM’10). Piscataway, NJ: IEEE, 2010: 1-5

[10]Yang Zhen, Wu Chenshu, Liu Yunhao, et al. Detecting outlier measurements based on graph rigidity for wireless sensor network localization[J]. IEEE Trans on Vehicular Technology, 2013, 62(1): 374-383

[11]Xiao Qingjun, Bu Kai, Wang Zhijun, et al. Robust localization against outliers in wireless sensor networks[J]. ACM Trans on Sensor Networks, 2013, 9(2): 24:1-26

[12]Yang Zhen, Jian Lirong, Wu Chenshu, et al. Beyond triangle inequality: Sifting noisy and outlier distance measurements for localization[J]. ACM Trans on Sensor Networks, 2013, 9(2): 1-20

[13]Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations and Trends in Machine Learning, 2011, 3(1): 1-122

[14]Combettes P L, Wajs V R. Signal recovery by proximal forward-backward splitting[J]. Multiscale Modeling and Simulation, 2005, 4(4): 1168-1200

[15]Gu Jingjing, Chen Songcan, Zhuang Yi. Localization in wireless sensor network using locality preserving canonical correlation analysis[J]. Journal of Software, 2010, 21(11): 2883-2891 (in Chinese)(顾晶晶, 陈松灿, 庄毅. 用局部保持典型相关分析定位无线传感器网络节点[J]. 软件学报, 2010, 21(11): 2883-2891)

[16]Candès E J, Recht B. Exact matrix completion via convex optimization[J]. Foundations of Computational Mathematics, 2009, 9(6): 717-772

[17]Cai J F, Candès E J, Shen Zuowei. A singular value thresholding algorithm for matrix completion[J]. SIAM Journal on Optimization, 2010, 20(4): 1956-1982

[18]Keshavan R H, Montanari A, Oh S. Matrix completion from noisy entries[J]. Journal of Machine Learning Research, 2010, 11(3): 2057-2078

[19]Ma Shiqian, Goldfarb D, Chen Lifeng. Fixed point and Bregman iterative methods for matrix rank minimization[J]. Mathematical Programming, 2011, 128(12): 321-353

[20]Keshavan R H, Montanari A, Oh S. Low-rank matrix completion with noisy observations: A quantitative comparison[C]Proc of the 47th IEEE Annual Allerton Conf on Communication, Control, and Computing. Piscataway, NJ: IEEE, 2009: 1216-1222

[21]Boyd S P, Vandenberghe L. Convex Optimization[M]. Cambridge, UK: Cambridge University Press, 2004

[22]Bruckstein A M, Donoho D L, Elad M. From sparse solutions of systems of equations to sparse modeling of signals and images[J]. SIAM Review, 2009, 51(1): 34-81

[23]Donoho D L. Compressed sensing[J]. IEEE Trans on Information Theory, 2006, 52(4): 1289-1306

[24]Wang Shusen, Zhang Zhihua. Colorization by matrix completion[C]Proc of the 26th AAAI Conf on Artificial Intelligence. Menlo Park, CA: AAAI, 2012: 1-7

[25]Li Kun, Dai Qionghai, Xu Wenli, et al. Three-dimensional motion estimation via matrix completion[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B: Cybernetics, 2012, 42(2): 539-552

[26]Cheng Jie, Ye Qiang, Jiang Hongbo, et al. STCDG: An efficient data gathering algorithm based on matrix completion for wireless sensor networks[J]. IEEE Trans on Wireless Communications, 2013, 12(2): 850-861

[27]Cabral R S, Torre F D L, Costeira J P, et al. Matrix completion for multi-label image classification[C]Proc of the 25th Annual Conf on Neural Information Processing Systems (NIPS). Cambridge, MA: MIT Press, 2011: 190-198

[28]Ji Hui, Liu Chaoqiang, Shen Zuowei, et al. Robust video denoising using low rank matrix completion[C]Proc of the 23rd IEEE Conf on Computer Vision and Pattern Recognition (CVPR). Piscataway, NJ: IEEE, 2010: 1797-1798

[29]Recht B, Fazel M, Parrilo P A. Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization[J]. SIAM Review, 2010, 52(3): 471-501

[30]Toh K C, Yun S. An accelerated proximal gradient algorithm for nuclear norm regularized linear least squares problems[J]. Pacific Journal of Optimization, 2010, 6(1): 615-640

[31]Lin Zhouchen, Chen Minming, Ma Yi, et al. The augmented lagrange multiplier method for exact recovery of corrupted low-rank matrices[EBOL]. (2010-09-26) [2014-09-27]. http:arxiv.orgpdf1009.5055

[32]Larsen R M. PROPACK—Software for large and sparse SVD calculations[CPOL]. (2010-09-26) [2014-09-27]. http:sun.stanford.edu～rmunkPROPACK

Xiao Fu, born in 1980. PhD. Professor and PhD supervisor of Nanjing University of Posts and Telecommunications. His main research interests include wireless sensor networks (WSNs).

Sha Chaoheng, born in 1990. Master candidate of Nanjing University of Posts and Telecommunications. His main research interests include wireless sensor networks (WSNs).

Chen Lei, born in 1975. PhD. Associate professor of Nanjing University of Posts and Telecommunications. His main research interests include machine learning.

Sun Lijuan, born in 1963. PhD. Professor and PhD supervisor of Nanjing University of Posts and Telecommunications. Her main research interests include wireless sensor networks (WSNs).

Wang Ruchuan, born in 1943. Professor and PhD supervisor of Nanjing University of Posts and Telecommunications. His main research interests include wireless sensor networks (WSNs).

中图法分类号TP391

基金项目：国家自然科学基金项目(61373137,61373017,61171053,61373139);江苏省高校自然科学研究计划重大项目(14KJA520002);江苏省“六大人才高峰”基金项目(2013-DZXX-014);江苏省“青蓝工程”项目;江苏高校优势学科建设工程项目-信息与通信工程

收稿日期：2014-10-08；修回日期：2015-02-28

This work was supported by the National Natural Science Foundation of China (61373137,61373017,61171053,61373139), the Major Program of Jiangsu Higher Education Institutions (14KJA520002), the Six Industries Talent Peaks Plan of Jiangsu (2013-DZXX-014), the Jiangsu Qinglan Project, and a Project Funded by Priority Academic Program Development of Jiangsu Higher Education Institutions.