中心型圆锥曲线内接三角形外心的一个性质研究

宋汶钊　王海峰

摘 要：本文修正了中心型圆锥曲线内接三角形外心的一个性质，提出并解决了三个问题。首先分析了以往错误推理的原因，接着修正了中心型圆锥曲线三角形外心的一个性质，在此基础上，探索了具有上述性质的中心型圆锥曲线内接三角形面积最值的存在性。本文的研究对于中心型圆锥曲线的教学有较好的借鉴和指导作用。

关键词：中心型圆锥曲线；椭圆；双曲线；内接三角形

一、提出问题

笔者首先就张敬坤在《数学通讯》期刊中的“圆锥曲线内接三角形外心的一组性质”（以下简称“例文”）进行了研究。例文研究了三种圆锥曲线内接三角形外心的一个性质，并且基于反证法得到了圆锥曲线内接三角形外心的一组结论：

结论1：椭圆内接三角形外心不会与其中心重合。

结论2：双曲线内接三角形外心不会与其中心重合。

结论3：抛物线内接三角形外心不会与其焦点重合。

事实上，经由图形直观地分析以及严格数学论证，我们发现例文给出的结论1和结论2是错误的，仅有结论3是正确的。

本文试图探讨有中心的圆锥曲线，如椭圆和双曲线（以下称中心型圆锥曲线）的内接三角形外心的性质。

我们首先以椭圆为例，通过图形直观分析椭圆内接三角形外心的特征。

设椭圆O：（a>b>O），以椭圆中心O为圆心，以半径a>r>b作圆，则圆O与椭圆必有四个交点A，B，C，D，则上述任意三个点组成的椭圆内接三角形的外心就是椭圆的中心O，如图1所示。易知，△ABC为直角三角形，其外心与椭圆的中心重合。

根据以上事实，本文提出并探讨以下问题：

Q1：对于中心型圆锥曲线，例文看似严密论证的不足之处在哪里？

Q2：中心型圆锥曲线的内接三角形外心与其中心是否能够重合？

Q3：中心型圆锥曲线的内接三角形外心与其中心重合时（下面简称满足（Q2）），内接三角形面积的最大（小）值是否存在？

二、分析问题

1.探究例文的问题所在

我们仔细分析例文后，发现其问题所在：例文在推理中用到△ABC的外心O在△ABC各边的中垂线上，在没有仔细论证的情况下，想当然认为是图2中的情形，认为OD斜率与BC斜率的乘积为-1。事实上，由于O点与D点重合，OD的斜率是不存在的。而例文的证明以OD⊥BC为前提条件，这对于图1情形来说，显然是不妥当的。由此，我们得到问题Q1的结论。

结论1：例文的论证不足之处在于，使用可能不存在的图形来论证，所以得出了错误的结论。

由结论1可得，在探索一个问题时，仅靠直观分析是不够的，还应以严格的推理为基础。

2.探索中心型圆锥曲线的内接三角形外心的性质

实际上，上述四组解刚好对应着图1中的A，B，C，D四个点。任意取3点可以构成一个三角形，记为△ABC，则此△ABC为直角三角形。根据直角三角形的性质有：斜边AC的中点就是△ABC的外心，即O（0，0）。

由上面的分析可知，对于任意一个椭圆来说，一定存在内接三角形，使得该三角形外心与椭圆的中心重合，且该三角形为直角三角形。

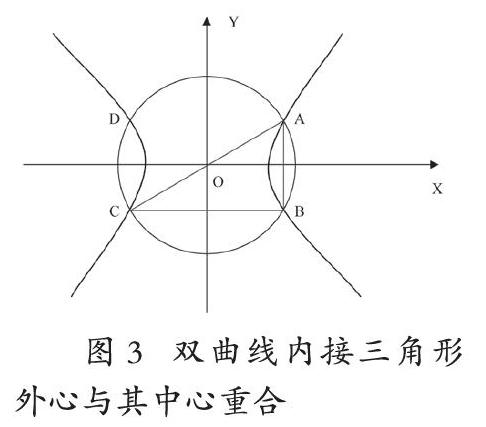
需要注意的是，由于b

对于双曲线O：（图3），我们同理可得类似的结论：

对于任意一个双曲线来说，一定存在内接三角形，使得该三角形外心与双曲线的中心重合，且该三角形为直角三角形。类似可知，该直角三角形的顶点不能落在双曲线的顶点上。

综上，我们得到中心型圆锥曲线内接三角形外心的性质特征：

结论2：对于任意一个中心型圆锥曲线来说，一定存在内接三角形，使得该三角形外心与这个圆锥曲线椭圆的中心重合，且该三角形为直角三角形。

3.探究满足（Q2）的中心型圆锥曲线内接三角形面积最大（小）值是否存在

因此，当θ=，时有S→∞，故不存在最大值；当θ→∞，π，2π时，S→0，故不存在最小值。综上所述，我们得到下面的结论：

结论3：满足条件（Q2）的中心型圆锥曲线内接三角形中，椭圆内接三角形面积存在最大值ab，不存在最小值（可以无限趋于0）；双曲线内接三角形面积不存在最大值（可以趋于无穷大），也不存在最小值（可以无限趋于0）。

三、结论

本文分析中心型圆锥曲线内接三角形外心的性质，提出并解决了三个问题（Q1，Q2和Q3）。

首先指出例文的错误在于根据一个不存在的图形进行推理（解决了Q1）；其次，我们证明了对于任意一个中心型圆锥曲线，一定存在内接三角形，使得该三角形外心与这个圆锥曲线椭圆的中心重合，且该三角形为直角三角形（解决了Q2）；最后，我们证明了满足条件（Q2）的中心型圆锥曲线内接三角形中，椭圆内接三角形面积存在最大值ab，不存在最小值（可以无限趋于0）；双曲线内接三角形面积不存在最大值（可以趋于无穷大），也不存在最小值（可以无限趋于0）（解决了Q3）。

本文的研究对于中心型圆锥曲线的教与学都具有较好的指导与借鉴意义。

参考文献：

张敬坤.圆锥曲线内接三角形外心的一组性质[J].数学通讯，2009（20）：30-31.