磁场引发石墨烯从金属态到绝缘态的相变

罗运文，李秀燕

闽南师范大学物理与电子信息工程系，福建漳州 363000



磁场引发石墨烯从金属态到绝缘态的相变

罗运文，李秀燕

闽南师范大学物理与电子信息工程系，福建漳州 363000

摘要：基于哈伯德模型，用微扰法计算磁场中石墨烯从金属态到绝缘态相变的临界值．研究发现，加入强磁场后，由于发生了量子霍尔效应，石墨烯的电子态和空穴态在零能级发生简并，因此零能级只能容纳1个电子，另一电子只能占据更高的朗道能级，这相当于增加了电子之间的相互作用能．磁场增大了电子之间的相互作用能，引起石墨烯从金属态向绝缘态的相变．

关键词：凝聚态物理学；石墨烯；哈伯德模型；量子霍尔效应；微扰法；金属-绝缘态相变

超流态(金属态)到绝缘态相变是物理中常见的现象，半导体中电子处于周期性势阱中，由于量子隧穿效应，价电子处于金属态，可以自由穿行于整个晶体中，加上电场后，电子会约束在实空间中，发生布拉格振荡，这是一种从金属态到绝缘态的相变．光晶格中的冷原子(玻色爱因斯坦凝聚粒子)，通过调节势阱的深度，能够引发从超流态到莫特绝缘态的量子相变[1-4]．通过改变两束激光的相对频率还可以让处于光晶格中的原子相对于光晶格受到一个常力，由此模拟电子在晶体中受到的电场力而产生布拉格振荡[5-6]．石墨烯性能独特，具有六边形单层碳原子结构，是一种理想的二维体系. 它的元激发粒子是一种无质量的费米子，可以用狄拉克方程描述，在强磁场中，会形成分立的朗道能级[7-9]．石墨烯中的电子处于周期性的势阱中，由于势阱较浅，电子不受束缚，因此石墨烯有良好的导电性，呈现出金属性． Gorbar等[10-11]计算了石墨烯的能谱，结果表明，加入磁场后，导带与价带之间会出现能隙，因此导致了石墨烯从金属态到绝缘态的相变，这一现象已经在实验中得到证实[12]．从相变的角度来看，是因为磁场增加了电子之间的相互作用能而引起相变．本研究用微扰方法[13]计算了磁场中石墨烯的相变临界值并给出相变曲线，发现磁场增加了复合玻色子(电子加磁通量子)之间的相互作用能，从而引发石墨烯从超流态(金属态)向绝缘态的相变．

1从超流态到绝缘态的相变

周期性势阱中的电子处于金属态还是绝缘态，是由相邻势阱间跃迁能J和同一势阱中的相互作用能U共同决定的.如果跃迁能大而相互作用能小，电子就可自由穿行于整个空间，处于金属态；反之，电子会被束缚在势阱中而处于绝缘态．未加入磁场时，石墨烯中的价电子处于周期性的势阱中，处于同一势阱中的零能级可以容纳自旋相反的两个电子，因此这时电子的相互作用能U较小，由于势阱较浅，跃迁能J很大，所以价电子不受束缚处于金属性态(超流态)，呈现出良好的导电性．加入强磁场后，体系发生了反常量子霍尔效应[14]，由于石墨烯特有的性质，电子态和空穴态在零能级简并，因此零能级只能容纳1个电子，另外1个电子只能占据更高的能级，这相当于增加了电子之间的相互作用能U. 量子霍尔效应使电子和磁通量子构成了复合的玻色子，发生了凝聚[15]，因此可以用哈伯德模型(Hubbard model)描述．为了简单起见，本研究中复合玻色子(电子+磁通量子)被称为粒子．忽略各个势阱中单个粒子的能量εi， 哈密顿量[16]为

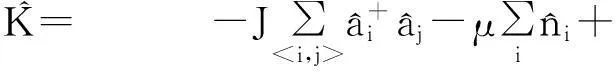
K^= -J∑^a+i^aj-μ∑i^ni+

(1)

图1为微扰过程中，势阱中电子分布的初态和末态示意图(B表示磁场)．

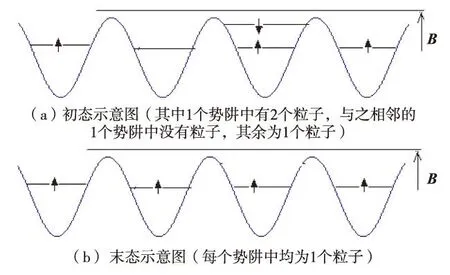
图1　石墨烯初态和末态示意图Fig.1　Schematic diagram of electron initial state and finial state in graphene

(2)

(3)

其中,

(4)

这里， Kσ为第i个势阱中粒子数为σ的能量； z为与第i个势阱相邻的势阱数，如一维势阱为2，石墨烯系统为3．

将式(4)代入式(3)，可得

(5)

另外，从系统来看，跃迁1个粒子引起的能量改变为

ΔE=-J

(6)

则由式(5)和式(6)可得

(7)

下面计算从超流态到绝缘态的临界值．设

(8)

则函数f (μ)的极值可从式(8)得到

(9)

由式(9)可得

(10)

将式(10)代入式(8)，可得

(11)

由式(7)和式(11)可得

(12)

由σ=1和z=3可得到石墨烯的相变临界值为

(13)

在式(13)中代入石墨烯格点间跃迁常数J=2.5 eV，可得临界相互作用能为U=43.7 eV. 未加磁场时，两个电子处于同一势阱中，设势阱的宽度为玻尔半径a0， 相互作用能为电势能U=ke2/a0， 代入参数e=1.6×10-19C, a0=5.3×10-11m， k=9×109N·m2/C2，得到U0≈28 eV,小于临界值，电子处于超流态；加入磁场后，发生了量子霍尔效应，每个电子束缚1个磁通量子而形成1个复合玻色子，由于复合玻色子带电，静电相互作用能仍然存在，但磁场提高了1个粒子的能级，与此同时，复合玻色子还存在交换能，这就增大了粒子之间的相互作用能，当相互作用能大于临界值时，就引发石墨烯从超流态到绝缘态的相变.

由式(7)可得到相变曲线，图(2)为σ=1时磁场中石墨烯的相图．其中，由“·”构成的是相变曲线．该相图分成两个区域，区域Ⅰ是绝缘区，区域Ⅱ为超流区．

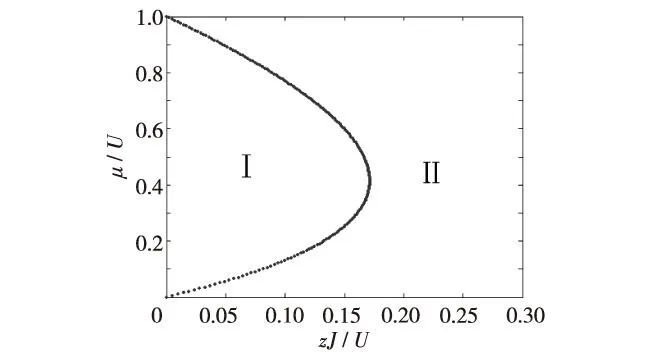
图2　磁场中的石墨烯相图Fig.2　Phase diagram of graphene in magnetic filed

在图2中，y轴μ/U为势阱深度，当μ/U=0(坐标原点)时，势阱深度为0，粒子不受约束(因为理想自由粒子在零温下化学势为0)， J无论为何值均处于超流态(区域Ⅱ)；当μ/U变大时，势阱深度增大．势阱深度的增大有两种影响：一方面抑制了粒子的隧穿能力；另一方面，当势阱深度增大时波函数会收窄，由于测不准原理，粒子动能会增大，这会反过来增加粒子的隧穿能力． μ/U由0开始增加时，第1种影响占主导地位，保持超流态就需要J/U增大，所以开始时J/U随μ/U的增大而增大；达到极大值后，第2种影响占主导地位，所以保持超流态需要的J/U反而减小．当μ/U=1时， J/U=0． 但μ/U不能大于1， 因为按模型的假定，当平均粒子数为1时，一个势阱中最多有两个粒子，所以相互作用能最大为U． 从式(7)可知(σ=1)， 当μ/U>1时，得到J/U<0为负值，此时无物理意义．

哈伯德模型应用到光晶格中的玻色凝聚粒子从超流态到绝缘态相变问题上取得极大的成功， U/J临界值的理论值约为35，实验值约为36，理论值与实验值吻合较好[4].以上理论是用平均场的方法推导出来的，本研究运用微扰法重现了上述结果并把它用于石墨烯体系．哈伯德模型讨论了0 K温度条件下，由于跃迁能和相互作用能的改变而引起的相变，并未考虑温度的影响．本研究把电子能够在周期性势阱中自由穿行的态定义为金属态，把电子约束在势阱中的状态定义为绝缘态，温度升高会增加电子的动能，使电子更难约束在势阱中，因此电子处于绝缘态的几率减小．从相图上可见，绝缘态所包含的面积(区域Ⅰ)减小，因此会减小相变临界值．

结语

用微扰法计算磁场中的石墨烯相变临界值，研究发现，在磁场中，因为量子霍尔效应，石墨烯中的电子和磁通量子构成了复合的玻色子，产生凝聚．由于石墨烯特有的能级特性，零能级只能容纳1个电子，因此磁场增加了同一势阱中电子的相互作用能，从而引起石墨烯从金属态向绝缘态相变．

引文：罗运文,李秀燕．磁场引发石墨烯从金属态到绝缘态的相变[J]. 深圳大学学报理工版，2016，33(2)：143-146.

参考文献/ References：

[1] Jaksch D, Bruder C, Cirac J I, et al. Cold Bosonic atoms in optical lattices[J]. Physical Review Letters, 1998, 81(15): 3108-3111.

[2] Bloch I, Dalibard J, Zwerger W. Many-body physics with ultracold gases[J]. Reviews of Modern Physics, 2008, 80(3): 885-964.

[3] Niu Qian, Zhao Xiangeng, Georgakis G A, et al. Atomic Landau-Zener tunneling and Wannier-Stark ladders in optical potentials[J]. Physical Review Letters, 1996, 76(24): 4504-4507.

[4] Markus G, Olaf M, Tilman E, et al. Quantum phase transition from a superfluid to a Mott insulator in a gas of ultracold atoms[J]. Nature, 2002, 415(6867): 39-44.

[5] Morsch O, Müller J H, Cristiani M, et al. Bloch oscillations and mean-field effects of Bose-Einstein condensates in 1D optical lattices[J]. Physical Review Letters, 2001, 87(14): 140402-140405.

[6] Dahan M B, Peik E, Reichel J, et al. Bloch oscillations of atoms in an optical potential[J]. Physical Review Letters, 1996, 76(24): 4508-4511

[7] Wallace P R. The band theory of graphite[J]. Physical Review, 1947, 71(9): 622-634.

[8] Neto A H C,Guinea F,Peres N M R,et al.The electronic properties of grapheme[J]. Reviews of Modern Physics, 2009, 81(1):109-162.

[9] Novoselov K S, Geim A K, Morozov S V, et al. Two-dimensional gas of massless Firac fermions in graphene[J]. Nature, 2005, 438(7065): 197-200.

[10] Gorbar E V, Gusynin V P, Miransky V A, et al. Magnetic field driven metal-insulator phase transition in planar systems[J]. Physical Review B, 2002, 66(4): 045108.

[11] Khveshchenko D V. Magnetic-field induced insulating behavior in highly oriented pyrolitic graphite[J]. Physical Review Letters, 2001, 87(20): 206401 .

[12] Kopelevich Y, Torres J H S, da Silva R R. Reentrant metallic behavior of graphite in the quantum limit[J]. Physical Review Letters, 2002, 90(15): 156402.

[13] 罗运文．用微扰方法来推导从绝缘态到超流态的临界值[J]．量子光学学报，2014，20(1)：65-67．

Luo Yunwen. Deduce the critical value for superfluid-to-insulator transition by using perturbation method[J]. Acta Sinica Quantum Optica, 2014, 20(1): 65-67.(in Chinese)

[14] 乔振华，任亚飞．石墨烯中量子反常霍尔效应研究进展[J]. 深圳大学学报理工版，2014，31(6)：551-560．

Qiao Zhenhua, Ren Yafei. Recent progress on quantum anomalous Hall effect in graphene[J].Journal of Shenzhen University Science and Engineering, 2016,33(2): 551-560.(in Chinese)

[15] Ezawa Z F. Quantum hall effects: field theoretical approach and related topics[M].2nd ed. Beijing: Peking University Press, 2012.

[16] Pethick C J, Smith H, Bose-Einstein condensation in dilute gases[M]. 2nd ed. London: Cambridge University Press, 2008: 433-434.

【中文责编：英子；英文责编：木南】

Magnetic field induced metal-insulator phase transition in graphene

Luo Yunwen†and Li Xiuyan

Department of Physics and Electronic Information Engineering, Minnan Normal University,Zhangzhou 363000, Fujian Province, P.R.China

Abstract：We calculate the critical value of condensed composite particles in graphene for metal-insulator phase transition in a magnetic field by using perturbation method based on the Hubbard model. We find that since the quantum Hall effect (QHE) occurs in high magnetic fields, the electron state and the hole state of graphene degenerate at zero energy level. Thus the lowest Landau level could only accommodate one electron and the other electron has to go to a higher Landau level. This is equivalent to increasing the interaction energy between electrons. The interaction energy increases due to the magnetic field, which induces the metal-insulator phase transition in graphene.

Key words：condensated matter physics; graphene; Hubbard model; quantum Hall effect; perturbation method; metal-insulator transition

作者简介：罗运文(1974—)，男，闽南师范大学副教授．研究方向：凝聚态物理．E-mail: yunwenluo@163.com

基金项目：福建省自然科学基金资助项目(2012D143)

中图分类号：O 469

文献标志码：A

doi：10.3724/SP.J.1249.2016.02143

Received：2015-12-11；Accepted：2016-01-31

Foundation：Natural Science Foundation of Fujian Province (2012D143)

† Corresponding author：Associate professor Luo Yunwen．E-mail: yunwenluo@163.com

Citation：Luo Yunwen, Li Xiuyan. Magnetic field induced metal-insulator phase transition in graphene[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(2): 143-146.(in Chinese)

【物理 / Physics】