不同区划方案对宏观交通事故建模的影响

黄合来, 许鹏鹏, 翟晓琪

(中南大学 交通运输工程学院，湖南 长沙 410075)



不同区划方案对宏观交通事故建模的影响

黄合来, 许鹏鹏, 翟晓琪

(中南大学 交通运输工程学院，湖南 长沙 410075)

摘要：依托美国佛罗里达州Hillsborough县历史数据，分别提取人口普查单元组、交通分析小区、人口普查区、邮政投递区等4种区划方案的事故数据、路网交通特征数据和经济-社会-人口数据；基于贝叶斯方法构建负二项条件自回归模型，从模型拟合度、模型估计参数、小区事故黑面识别等3个方面定量评价不同区划方案对宏观交通安全分析结果的影响.研究表明：宏观交通安全分析结果会随着空间单元划分方式不同而产生显著差异；小区数目越少，事故预测越为准确；对比人口普查单元组、人口普查区和邮政投递区，基于交通分析小区的模型拟合度最低；变量中等家庭收入对分区规模最不敏感，其参数估计结果具有稳健性和可靠性.

关键词：宏观交通安全分析； 区划方案； 贝叶斯估计； 条件自回归模型

交通安全规划已成为当前国际道路交通业界和学术界最为前沿的研究方向之一[1]，其要求将交通安全考虑到交通规划的各个层面，强调从宏观到微观对安全水平的预测和规划.交通规划层面的影响因素与交通安全水平的关联方法，即宏观事故预测模型，已成为该领域核心技术之一.

国外已经开展大量定量研究来分析不同规划层面的影响因素与交通安全水平的关系.其空间分析单元包括州[2]、县[3-4]、行政区划[5]、交通分析小区(traffic analysis zones, TAZs)[6-8]、人口普查区(census tracts, CTs)[9]、邮政投递区(zone improvement plan codes, ZIP)[10]等.已有研究主要从道路网络特征(公路里程、路网密度、交叉口密度)[3-6]，交通流特征(限速、平均行驶速度、交通流量)[3-6,9]，天气特征(降雨量、降雪量、年降雨天数)[3]，土地利用特征[7]，以及社会-经济-人口特征(人口、年龄、性别、就业、收入等)[3,4,9-10]等若干方面进行分析.方法层面，常用的负二项模型和泊松-对数正态模型假定事故的分布在空间上相互独立，而现实中事故数据具有空间聚集特征.为克服上述缺陷，通过引入条件自回归(conditional autoregressive, CAR)残差项以反映相邻小区间可能存在的空间关联，贝叶斯条件自回归模型被广泛应用于宏观交通安全分析中[3,4,8,10-11].

由于宏观事故建模依赖于事故数据和规划层面数据以小区的方式聚合呈现，其结果可能会随着空间单元划分方式不同而变化[11].现阶段，尚没有文献深入探讨不同区划方案对宏观交通安全分析结果的影响.

本文依托美国佛罗里达州Hillsborough县历史数据，分别提取人口普查单元组、交通分析小区、人口普查区、邮政投递区层面的事故数据、路网交通特征数据和经济-社会-人口数据；基于贝叶斯方法构建负二项条件自回归模型；从模型拟合度、模型估计参数、小区事故黑面识别等3个方面定量评价不同区划方案下同一事故预测模型结果的差异性.

1数据准备

1.1区划方案介绍

获取4种区划方案，人口普查单元组、人口普查区、交通分析小区和邮政投递区.交通分析小区来源于中佛罗里达区域规划模型，其余3种区划方案来源于美国人口普查局拓扑地理信息编码系统.

人口普查单元(census blocks)是美国最小的地理区划单元，每个单元人口一般控制在85人次左右.Hillsborough县共包含17 388个人口普查单元，其面积的中位数为0.02 km2.因此，较难在人口普查单元上提取有用的人口统计信息.

人口普查单元组(block groups, BGs)由人口普查单元聚合而来，是人口普查数据发布的最小区划单元.一个人口普查单元组一般包含600～3 000人.

人口普查单元组聚合得到人口普查区.每个人口普查区的人口保持在1 200～8 000人次，小区内人口特征、经济收入、生活水平等具有同质性.

交通分析小区是研究交通生成与分布的基本空间单元，其划分通常基于人口普查单元，以河流、桥梁、山川、铁路等屏障作为边界线，并保证小区内土地利用属性的同质性[12].

邮政投递区是美国邮政服务采用的一种区划方案.ZIP是地区改进计划(zone improvement plan)的简称，其喻示邮件可以更有效、更快捷地送至目的地.

Hillsborough县共包含795个人口普查单元组、738个交通分析小区、249个人口普查区和52个邮政投递区，小区面积的中位数分别为0.99、1.24、4.19和27.39 km2.

1.2数据收集

道路交通数据来源于佛罗里达州运输部道路调查报告和Hillsborough县GIS(geographical information system)地图.基于GIS平台对数据进行集聚处理，获得小区层面的路网交通特征数据如下：

(1) 路段总长度：每个小区内道路中心线总里程数；

(2) 按限速值分类的路段长度：限速值为40 km·h-1的路段长度；限速值为56 km·h-1的路段长度；限速值为72 km·h-1的路段长度；限速值为89 km·h-1的路段长度；以及限速值为105 km·h-1的路段长度；

(3) 交叉口数目：每个小区内交叉口的数目；

(4) 车辆行驶里程(vehicle mile traveled, VMT)：小区内每条路段的年平均日交通量与其长度的乘积.

经济-社会-人口数据来源于美国人口普查局2000年人口普查数据.基于AcrMap空间关联工具对数据进行映射处理，获得各区划方案的变量如下：

(1) 小区面积：每个小区的陆地面积(去除河流和湖泊的占地面积)；

(2) 常住人口数：基于2006年总人口对各个小区的人口进行比例扩算；

(3) 人口性别分布：每个小区男性/女性人口数；

(4) 人口年龄分布：每个小区年龄为15岁及以下的人口数，年龄处于16～64岁的人口数，年龄为65岁及以上的人口数；

(5) 中等家庭收入：小区内所有家庭收入的中位数.

1.3数据处理

选取事故总数作为模型的响应变量.对于模型的解释变量，车辆行驶里程是交通事故发生的直接机会变量，将其首先加入模型.交叉口是交通事故多发点.在控制路段长度的前提下，采用交叉口密度(交叉口数目与道路总长度的比值)来反映交通状况的复杂程度.不同限速策略可能会对交通安全产生显著影响.在控制路段长度的前提下，采用不同限速路段长度占小区道路总长度的比例来考量限速策略与交通安全的关系.由于限速89和105 km·h-1的路段所占比例较低，为避免变量冗余，将两者合并.采用人口密度(人口数目与小区面积比值)以反映小区人口密集程度.采用女性人口比例和不同年龄段人口比例来表征小区人口年龄性别特征.对于小区经济发展水平，采用中等家庭收入作为指标变量.变量的描述性统计结果见表1.

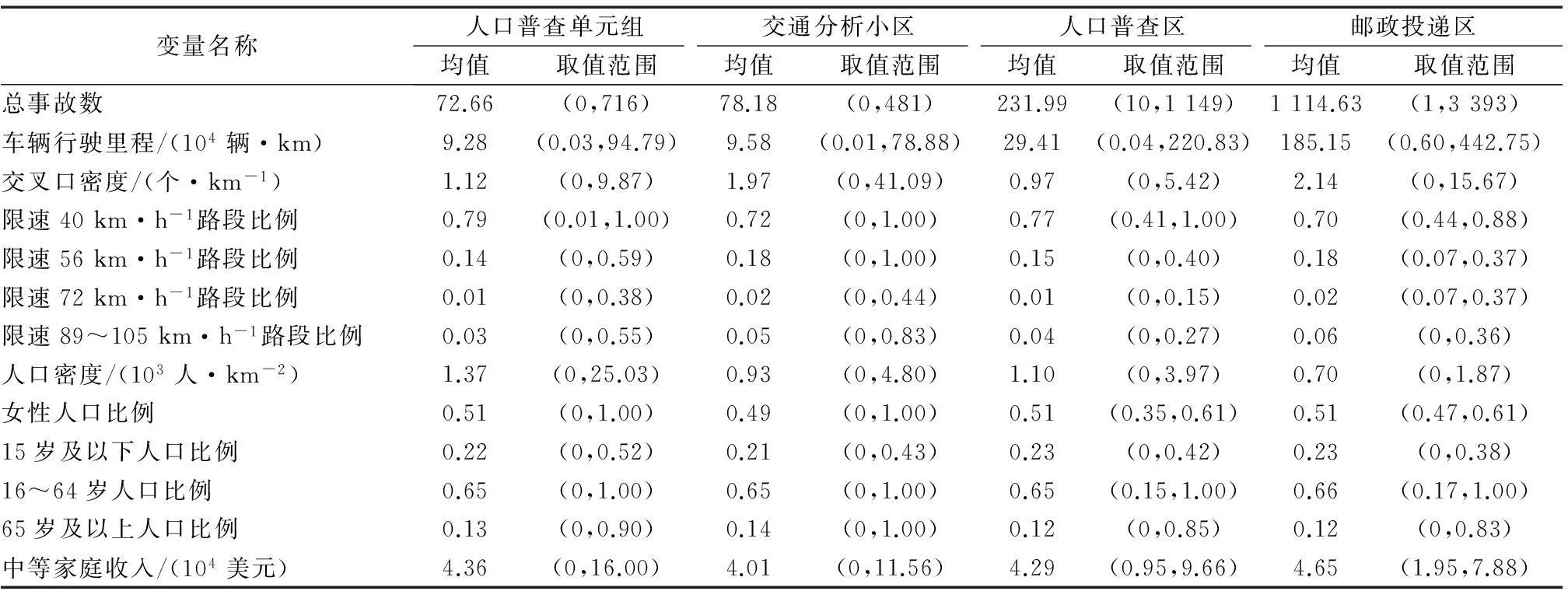
表1　变量描述性统计表

2模型建立

2.1负二项条件自回归模型

Yi～Negbin(λi,γ)

(1)

式中：λi为事故的期望值；γ为离散系数；VMT,i为第i个小区的车辆行驶里程；Xik表示第i个小区第k个解释变量；β0、β1和βk为待估系数.φi为满足条件自回归的先验分布[8]：

其中：τc为精度参数；wij为空间邻接矩阵W的元素.若第i个小区与第j个小区相邻，则wij=1，否则为0.

在贝叶斯估计中，为模型参数设定无信息先验分布如下：

βk～N(0,1 000)

1/γ～Gamma(0.01,0.01)

τc～Gamma(0.01,0.01)

使用WinBUGS软件[13]对上述模型进行标定.

采用安全可提高空间指标[14]对事故黑面进行判别：

Pi=λi-

(2)

Pi值越大，小区i安全改善的潜能越大.

2.2模型评价标准

采用偏差信息准则(deviance information criterion,DIC,以DIC表示)、R2、均方预测标准误差(normalized mean squared prediction error, NMSPE, 以NMSPE表示)对待选模型进行科学评价.

类似赤池信息准则，DIC综合考虑模型拟合度和复杂度，其计算方法如下[15]：

(3)

采用R2对模型整体拟合度进行评价：

(4)

为避免样本数目差异，采用NMSPE评价模型预测精度，表示如下：

(5)

NMSPE值越小，模型的预测能力越强.

3结果分析

3.1模型拟合度评价

依据模型拟合度和简约度对解释变量进行筛选，并避免高度相关的变量加入同一模型.剔除在所有区划方案中均不显著的变量，模型估计结果见表2所示.结果表明：(1)随着小区数目增多，DIC值显著增大.其原因可能为随着样本数增多，模型复杂度逐渐增大.因此，仅从DIC值无法客观判别不同区划方案下同一模型的优劣.(2)对于人口普查区和邮政投递区，模型拟合度最优，而交通分析小区层面的模型拟合度最低，R2值仅为0.68.(3)随着小区数目逐渐减少，NMSPE值逐渐降低.这说明本研究所采取的宏观区域指标在小区数目较小的情况下对事故的预测更为准确.

3.2模型参数估计结果

由表2可得出以下结论：(1)对于人口普查单元组、交通分析小区和邮政投递区，显著的解释变量数均为5个，而人口普查区中显著的解释变量有4个；(2)随着小区数目逐渐减少，变量影响系数的标准差逐渐增大；(3)空间自相关效应在4种区划方案中均显著，说明有必要考虑小区间的空间相关性.

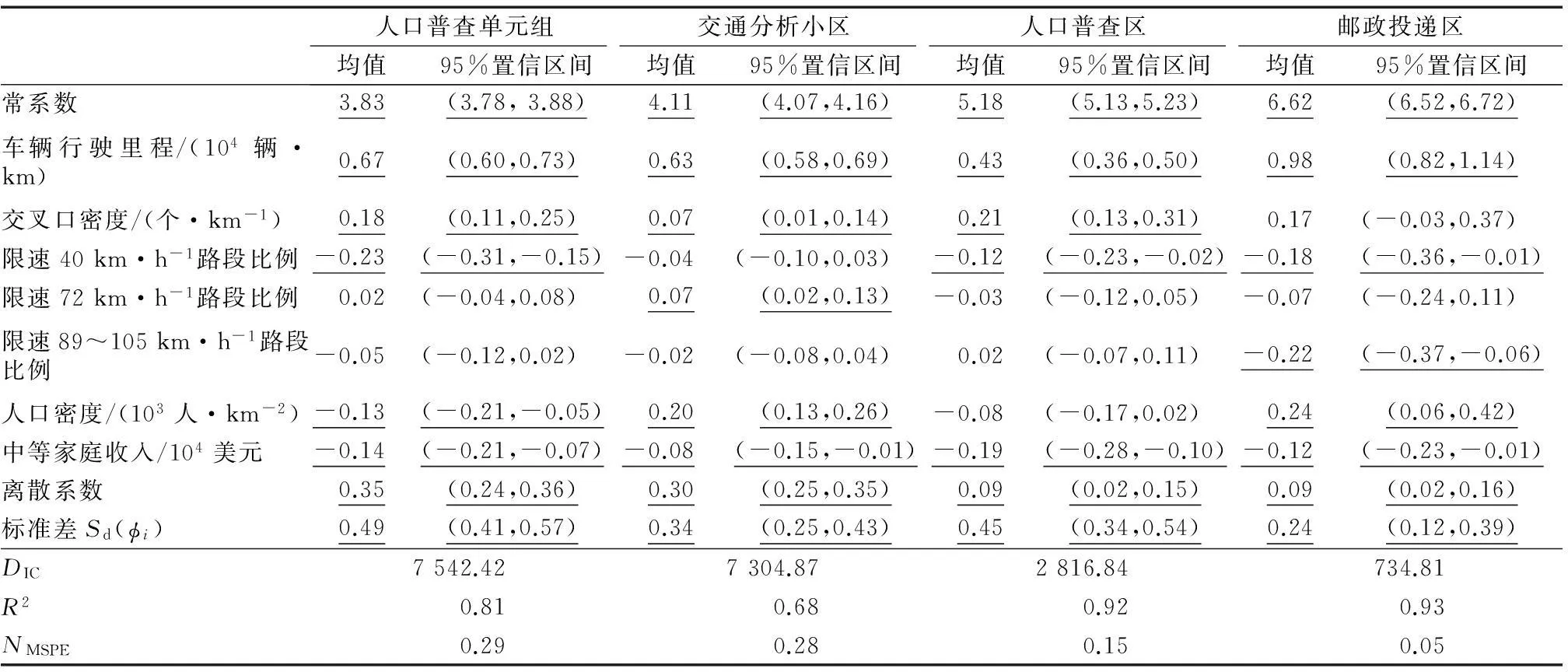
表2　模型估计结果

注：加下划线的数值表明95%统计显著.

车辆行驶里程与事故显著正相关.这说明随着车辆行驶里程增加，居民出行活动增加，事故频次显著增长.此外，该变量的影响系数最大，说明车辆行驶里程是预测小区交通安全水平的主要指标.另一方面，不同区划方案间该变量的估计参数差异较大.例如，对于人口普查区，其影响系数仅为0.43，而在邮政投递区中增至0.98.

交叉口是交通事故多发点.除了邮政投递区，交叉口密度在其余三种区划方案中均与事故频次显著正相关.给定路段长度和车辆行驶里程，交叉口数目越多，事故发生的频次越高.

路段限速的设定要综合考虑区域特征、道路设计标准、交通运行状况等因素.此外，路段限速值并不能够客观地反映交通流特征，因此其与交通安全的关系错综复杂[8].本研究中，对于人口普查单元组、人口普查区和邮政投递区，增加限速40 km·h-1路段，小区的安全水平将显著提高；对于变量限速72 km·h-1路段比例，其在交通分析小区中与事故显著正相关，而在其余区划方案中均不显著；变量限速89～105 km·h-1路段比例仅在邮政投递区中显著.

以往研究表明，人口密集程度越高的小区，事故频次越高[4].对于交通分析小区和邮政投递区，人口密度均与事故显著正相关，而其在人口普查单元组中与事故显著负相关.该结果有违常识.变量相关性检验表明：人口密度与事故频次95%显著负相关，皮尔逊相关系数为-0.17.

对于4种区划方案，中等家庭收入均与事故显著负相关，说明小区经济发展水平越高，事故频次越低，交通状况越为安全.其原因可能为这类小区的道路级配较高，道路安全设施配置相对齐全；另一方面，富有小区居民的安全意识可能较高，其购买和拥有高安全性能汽车的可能性较高.

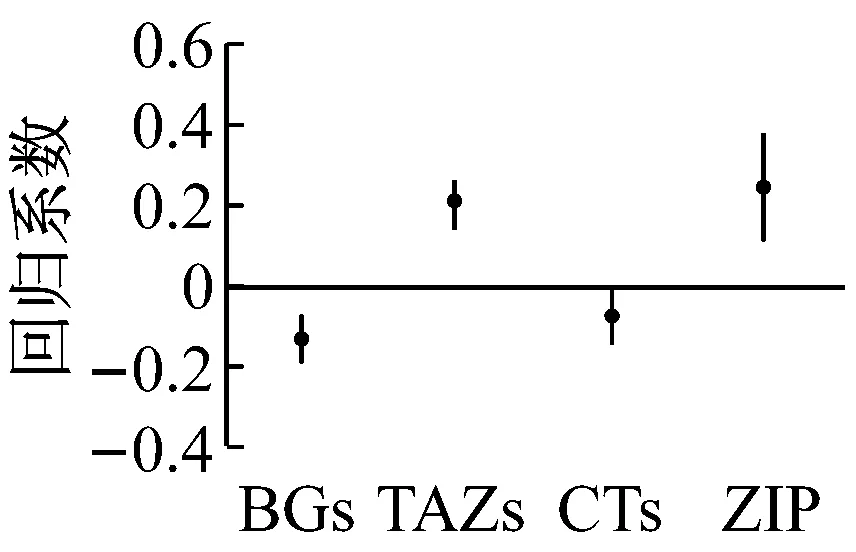
为定量评价表2模型参数估计结果差异是否统计显著，对模型参数进行均值偏差标准检验(standard difference in means test).图1箱体图代表模型变量影响系数的均值±1.5倍标准差.假定S为标准差，当满足条件：

(6)

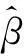
如图1，变量中等家庭收入对小区区划方式最不敏感，其参数估计结果具有稳健性和可靠性.其余变量均存在差异95%置信区间上统计显著的情况.

a 车辆行驶里程

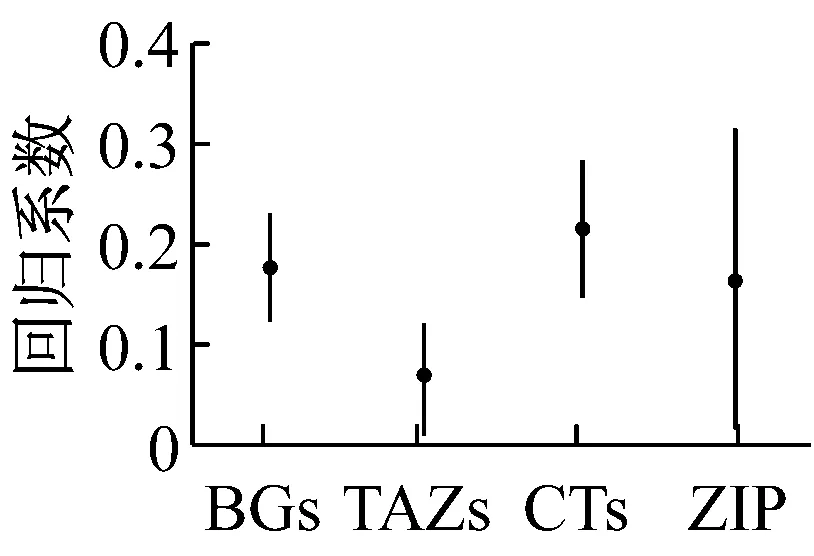
b 交叉口密度

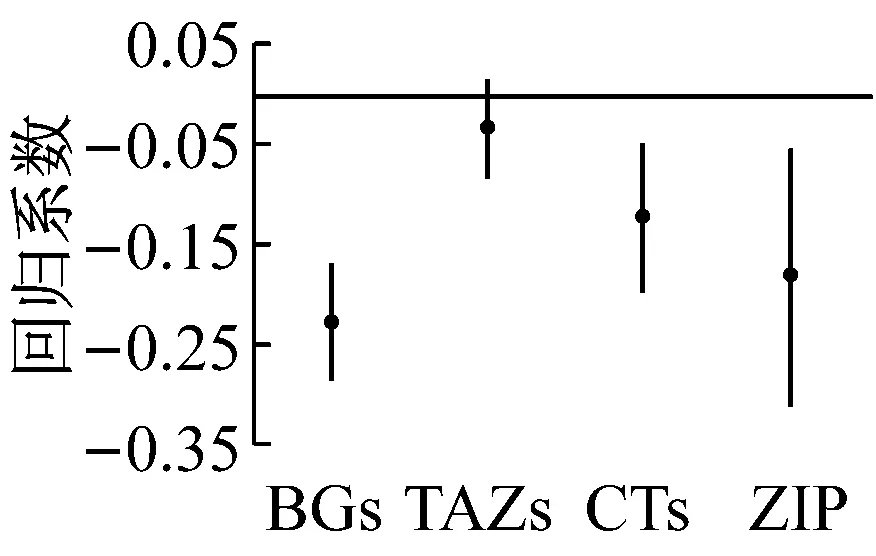
c 限速40 km·h-1路段比例

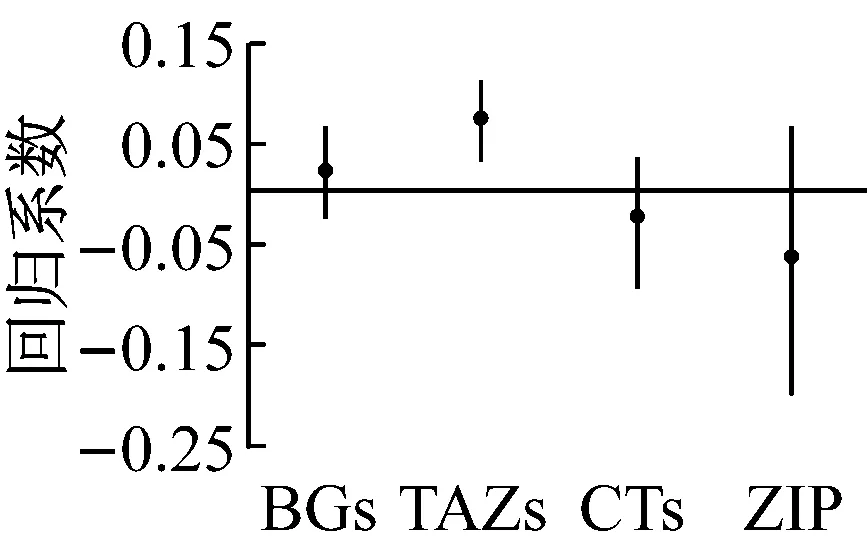
d 限速72 km·h-1路段比例

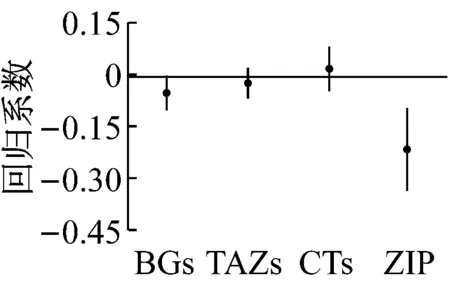
e 限速89～109 km·h-1路段比例

f 人口密度

g 中等家庭收入

3.3事故黑面识别

采用安全可提高空间指标，假定排名前20%的小区为事故多发区，结果如图2所示.可以看出，事故黑面会随着空间单元划分方式不同而变化.对于邮政投递区，事故黑面主要位于中部偏西南地区，而在其余三种区划方案中，事故黑面多集中于中部偏西地区.

4结语

基于实践数据，本文首次证实宏观交通安全分析结果会随着空间单元划分方式不同而产生显著差异.研究表明：(1)小区数目越少，事故预测越为准确；(2)对比人口普查单元组、人口普查区和邮政投递区，基于交通分析小区的模型拟合度最低；(3)变量中等家庭收入对分区规模最不敏感，其参数估计结果具有稳健性和可靠性；(4)实际中分区要保持适度规模.当小区数目较多时，一方面造成数据冗余并增加数据收集工作量，另一方面，处于小区边界上的事故将明显增多，可能导致边界效应；如若小区数目较少，将导致有效信息缺失，此外，以往研究表明[10]，小区数目越少，变量影响系数的标准差越大，显著变量的数目越少.

现阶段，宏观交通安全研究多采用交通分析小区作为基本空间分析单元.考虑交通分析小区的划分鲜有考虑安全相关因素，黄合来等[1]提出“交通安全分析小区”的概念，一方面，交通安全分析小区的划分应尽可能满足交通分析小区划分的基本原则；另一方面，小区聚合应遵循安全同质性原则.

交通安全分析小区的提出更大程度上是强调“将交通安全融入交通规划”这一理念.考虑交通规划实践，建议仍采用“交通分析小区”称谓，但在其区划过程中如何将交通规划层面的因素和交通安全相关因素有机融合，是一个值得探讨的科学问题.

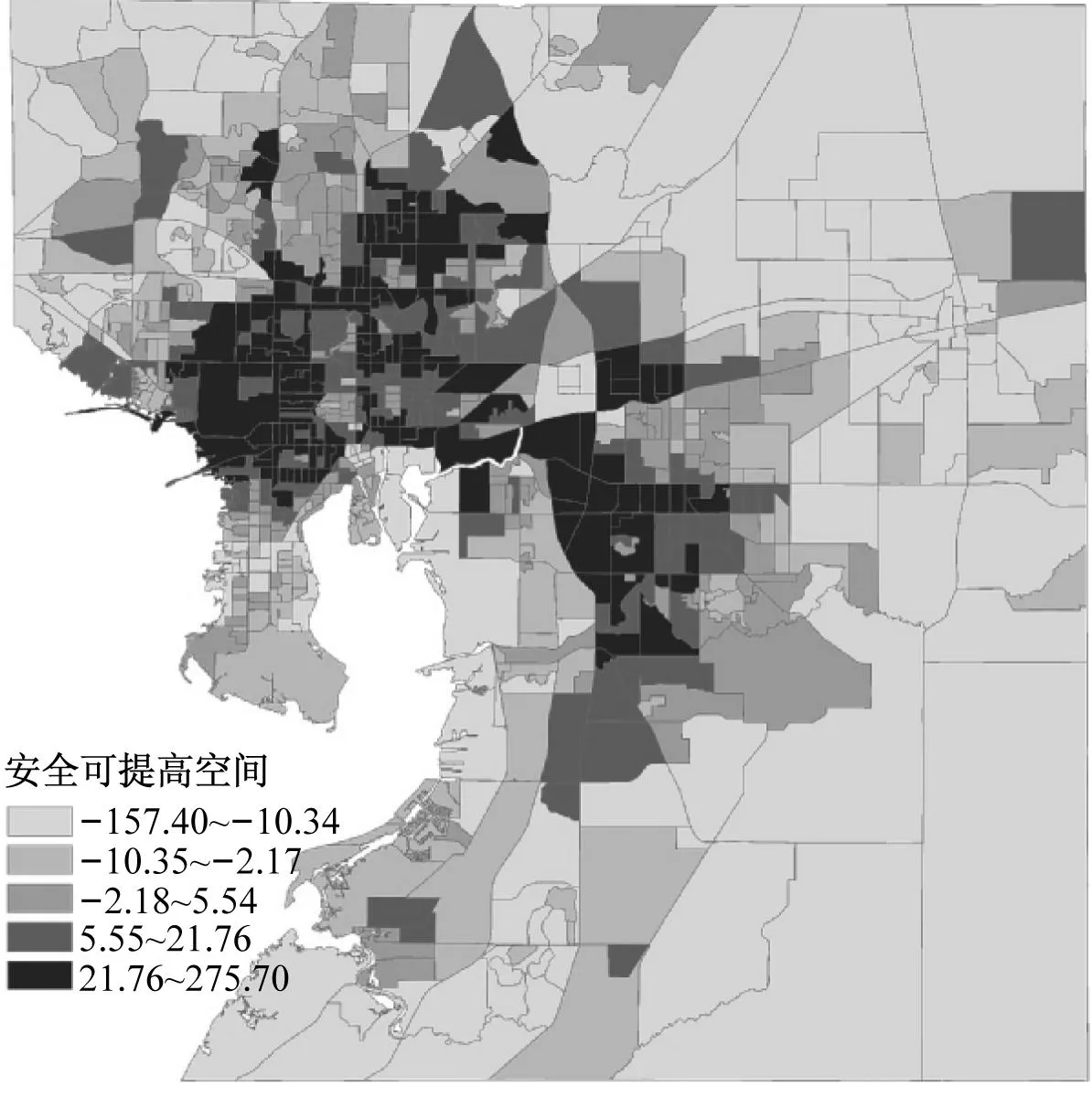
a 人口普查单元组

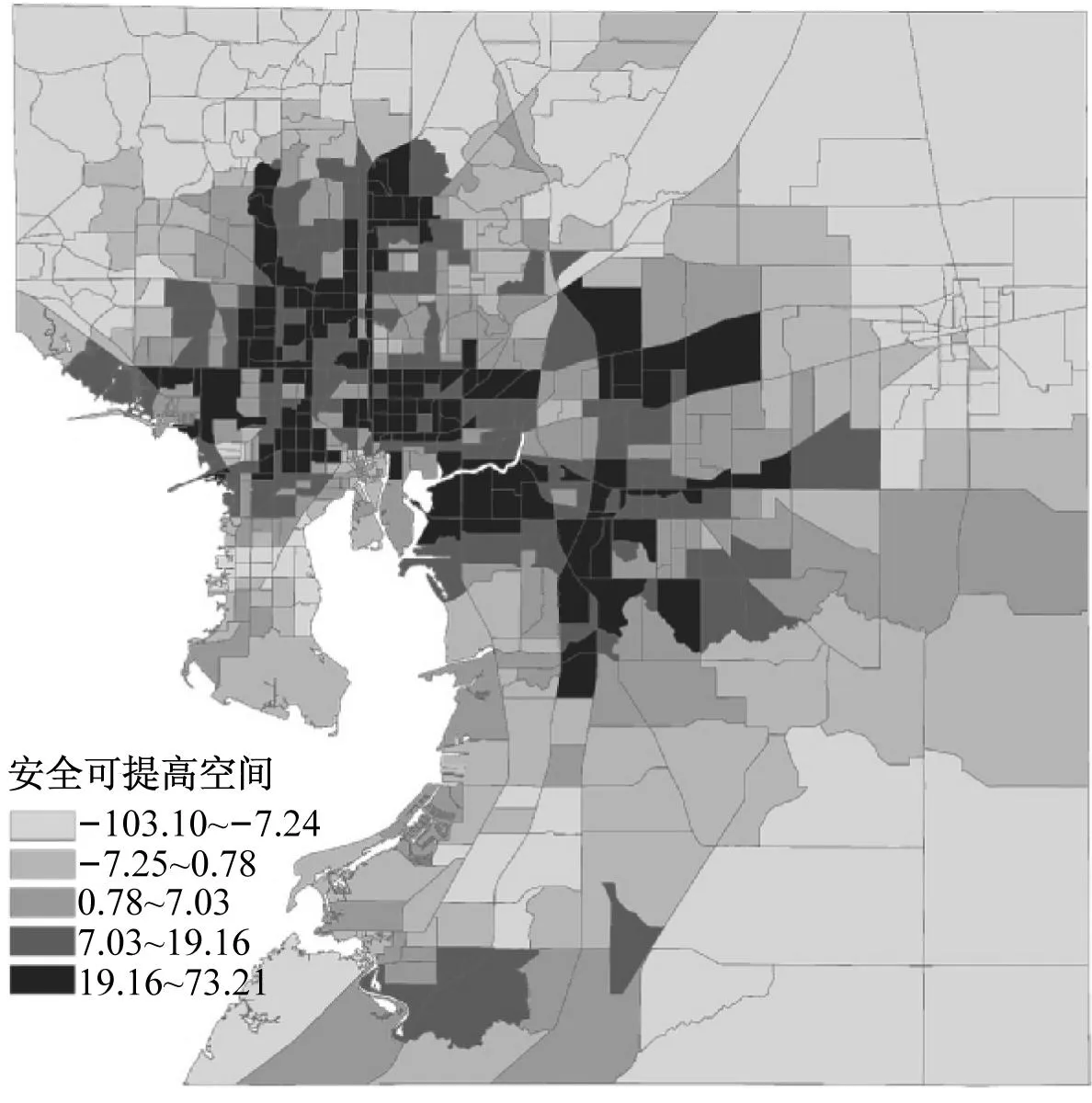
b 交通分析小区

c 人口普查区

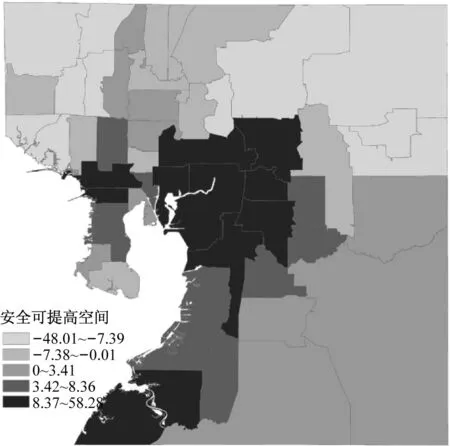
d 邮政投递区

参考文献:

[1]黄合来, 许鹏鹏, 马明, 等. 道路交通安全规划理论研究前沿[J]. 中国公路学报, 2014, 27(9): 90.

HUANG Helai, XU Pengpeng, MA Ming,etal. Cutting edge research on transportation safety planning: a technical review[J]. China Journal of Highway & Transport, 2014, 27(9): 90.

[2]Washington S, Metarko J, Fomunung I,etal. An inter-regional comparison: fatal crashes in the southeastern and non-southeastern United States: preliminary findings[J]. Accident Analysis & Prevention, 1999, 31(1-2): 135.

[3]Aguero-valverde J, Jovanis P P. Spatial analysis of fatal and injury crashes in Pennsylvania[J]. Accident Analysis & Prevention, 2006, 38(4): 618.

[4]Huang H L, Abdel-Aty M, Darwiche A L. County-Level crash risk analysis in Florida: Bayesian spatial modeling[J]. Transportation Research Board: Journal of the Transportation Research Board, 2010, 2148: 27.

[5]Haynes R, Jones A, Kennedy V,etal. District variations in road curvature in England and Wales and their association with road-traffic crashes[J]. Environment & Planning A, 2007, 39(5): 1222.

[6]Abdel-Aty M, Siddiqui C, Huang H L. Integrating trip and roadway characteristics in managing safety at traffic analysis zones[J]. Transportation Research Record: Journal of the Transportation Research Board, 2011, 2213: 20.

[7]Pulugurha S S, Duddu V R, Kotagirl Y. Traffic analysis zone level crash estimation models based on land use characteristics[J]. Accident Analysis & Prevention, 2013, 50: 678.

[8]Xu P P, Huang H L. Modeling crash spatial heterogeneity: random parameter versus geographically weighting[J]. Accident Analysis & Prevention, 2015, 75: 16.

[9]MacNab Y C. Bayesian spatial and ecological models for small-area accident and injury analysis[J]. Accident Analysis & Prevention, 2004, 36(6): 1019.

[10]Lee J, Abdel-Aty M, Choi K. Analysis of residence characteristics of at-fault drivers in traffic crashes[J]. Safety Science, 2014, 68: 6.

[11]Xu P P, Huang H L, Dong N,etal. Sensitivity analysis in the context of regional safety modeling: identifying and assessing the modifiable areal unit problem[J]. Accident Analysis & Prevention, 2014, 70: 110.

[12]Abdel-Aty M, Lee J, Siddiqui C,etal. Geographical unit based analysis in the context of transportation safety planning[J]. Transportation Research Part A: Policy and Practice, 2013, 49: 62.

[13]Spiegelhalter D J, Thomas A, Best N G,etal. WinBUGS version 1.4.1 User Manual[Z]. Cambridge: Medical Research Council Biostatistics Unit, 2003.

[14]王雪松, 李佳, 谢琨. 基于安全可提高空间的事故多发信控交叉口判别[J]. 同济大学学报: 自然科学版, 2015, 43(3): 410.

WANG Xuesong, LI Jia, XIE Kun. Signalized intersection hotspot identification based on potential for safety improvement[J]. Journal of Tongji University: Natural Science, 2015, 43(3): 410.

[15]Spiegelhalter D, Best N, Carlin B P,etal. Bayesian measures of model complexity and fit[J]. Journal of Royal Statistical Society B: Statistical Methodology, 2002, 64(4): 583.

Influence of Zonal Configurations on Macro-level Traffic Safety Modeling

HUANG Helai, XU Pengpeng, ZHAI Xiaoqi

(School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China)

Abstract：Based on the historic data from Hillsborough County, Florida, U.S., the zone-level factors including crashes counts, road network, traffic pattern, and various social economic factors were explicitly collected for four different zoning schemes, i.e. block groups, traffic analysis zones, census tracts, and zone improvement plan codes. Then, a Bayesian negative binomial model with conditional autoregressive prior was developed for each spatial units, respectively. The impacts of zonal variations on macro-level safety modeling were investigated mainly from three aspects, i.e. model performance, model parameter estimates, as well as crash hotspots identification. Results revealed that statistical results based on different aggregation configurations could be significantly different. Zoning schemes with less number of zones tend to have higher crash prediction precision. Compared with block groups, census tracts, and zone improvement plan codes, traffic analysis zones level model preforms worst in terms of model goodness of fit. The variable of median household income shows consistently significant effects on crash frequency and is robust to variation in data aggregation.

Key words：macro-level safety analysis; zoning schemes; Bayesian inference; conditional autoregressive model

文献标志码：A

中图分类号：U491.31

通讯作者：许鹏鹏(1990—)，男，工学硕士，主要研究方向为交通安全，空间数据分析.E-mail: pengpengxu@yeah.net

基金项目：国家自然科学基金项目(71371192)；霍英东教育基金会高等院校青年教师基金应用研究课题(142005)；湖南省杰出青年基金项目(2015JJ1017).

收稿日期：2015-04-23

第一作者： 黄合来(1979—)，男，工学博士，教授，博士生导师，主要研究方向为交通安全，交通规划和智能交通.

E-mail: huanghelai@csu.edu.cn