基于模糊多目标对策的雷达反干扰策略优化

翟　翔，贾仁耀，魏　元

（电子工程学院，合肥　230037）



基于模糊多目标对策的雷达反干扰策略优化

翟翔，贾仁耀，魏元

（电子工程学院，合肥230037）

摘要：考虑到单部雷达反干扰效能评估指标多样化、模糊且存在不同权重的情况，在对策论基础上提出了一种雷达反干扰策略优化模型，并在考虑局中人偏好情况下，设计了一种模糊多目标对策最优混合策略求解算法，为找出较优化的雷达反干扰策略以及为战场决策提供参考。

关键词：模糊多目标对策，雷达反干扰，策略优化

0　引言

在战场环境高度信息化、武器装备日益电子化的趋势下，争夺制信息权成为交战双方作战的重心。雷达干扰作为削弱、破坏敌雷达系统效能的主要作战手段之一，已直接关系到战争进程和结局。因此，采取雷达反干扰措施，消除或削弱敌干扰影响，保证己方雷达工作效能显得尤为重要。美军《FM3-36陆军电子战作战条令》［1］中指出，遂行电子防护“必须要了解己方电子装备可能面临敌方电子攻击的威胁以及弱点，要采取适当的行动保护己方作战能力不被敌方利用和攻击，最大限度地减小敌方针对己方作战力量的电子攻击行动的有效性”。由此可见，雷达干扰与雷达反干扰既有对抗性，也有针对性，这就要求在反干扰策略的选取中体现其竞争特性和主体差异性。

当前对雷达反干扰策略优化的研究，主要是选取抗干扰改善因子（EIF）等单一指标，应用对策论建立反干扰决策矩阵，从而求解得出最优混合策略。其在实际运用中仍存在指标单一、忽视雷达自身战术要求、难以给出精确支付值等不足。对此，本文针对攻防两方对不同雷达的指标权重存在偏好、对策矩阵中支付值不明确的情况，提出一种基于考虑局中人偏好信息的模糊多目标对策的雷达反干扰策略优化方法，并给出算例分析。

1雷达反干扰策略优化模型

假设我方单部雷达受到敌方一部或多部干扰机施放的干扰，且敌方干扰已经满足频率上、方向上、极化上对准的基本条件，我方雷达亦有反干扰措施若干。现要求通过建立对策模型，选取一种或几种反干扰措施，最大程度地消除或削弱敌方干扰的影响。

1.1主要雷达干扰与反干扰策略的选取

雷达反干扰策略分为技术措施和战术措施。因仅考虑单部雷达对抗，且难以量化战术措施效能，仅选取以下主要反干扰技术措施为策略集：

S1={频率捷变，恒虚警，MTD，宽限窄电路，脉冲压缩，副瓣抑制}

敌方干扰策略分为压制式干扰和欺骗式干扰，假定干扰方的策略集：

S2={瞄准式干扰，阻塞式干扰，扰频式干扰，距离欺骗式干扰，速度欺骗式干扰，角度欺骗式干扰} 1.2雷达反干扰效能评估指标体系的建立

现有的雷达反干扰效能评估指标评估准则主要包括信息准则、战术应用准则、功率准则、概率准则、时间准则等。单独运用一种评估准则选取雷达反干扰效能评估指标，往往不能全面反映雷达的反干扰效果。在此兼顾指标的明确性、可比性、完备性、独立性和层次性，建立以下雷达反干扰效能评估指标体系如图1所示。

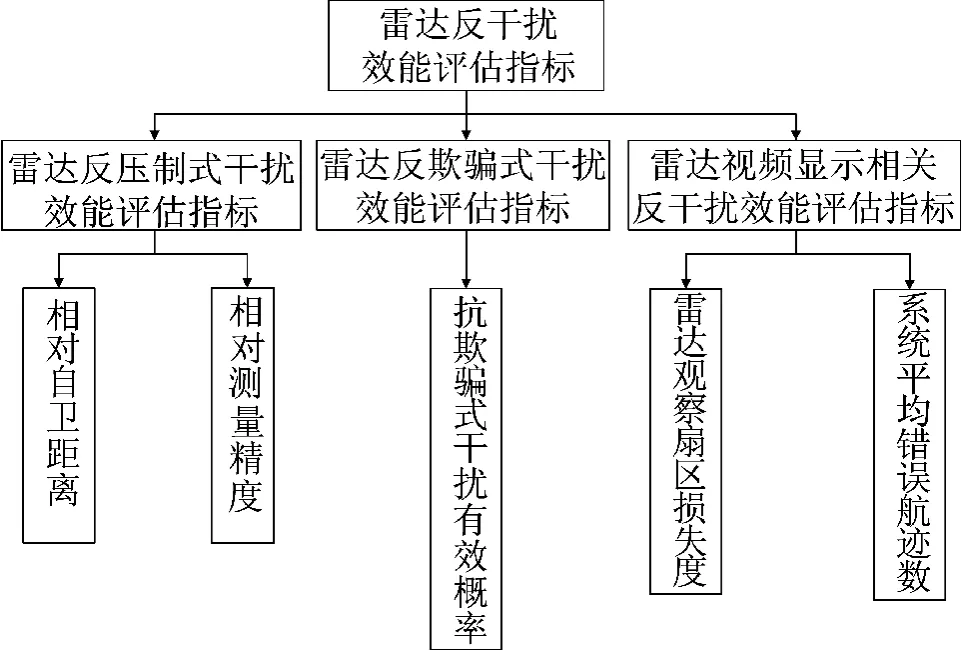
图1　雷达反干扰效能评估指标体系

1.3效能评估方法

评估反干扰效能既要考虑反干扰措施对某一指标的改善程度，又要考虑其对抗的干扰手段使该指标下降的程度，定义第i项反干扰措施和第j项干扰手段形成的局势，对某型雷达的第k项指标的反干扰效能支付值

其中ejk为第j项干扰手段对第k项指标的干扰效能，eijk为采用第i项反干扰措施后的改善效能。考虑到对策环境复杂，单一措施技术指标非固定值，支付值往往是模糊的，用模糊数a～ijk表示。

1.4指标权重的确定

在雷达干扰与反干扰的对抗过程中，反干扰方已掌握雷达特性和用途，干扰方在情报侦察与支援侦察阶段亦已获取相应雷达对抗情报，可认为双方对多个指标有相同偏好信息，即有相同权重向量w= （w1，w2，…，wN）T。

此处权重可针对不同作战任务、不同用途的雷达，通过基于专家打分的层次分析法求得。

2考虑局中人偏好信息的模糊多目标二人零和矩阵对策求解

2.1模糊多目标二人零和矩阵对策

假定有2个局中人P1和P2参与对策，其纯策略集合分别记为S1={α1，α2，…，αm}，S1={β1，β2，…，βn}，当局中人P1选取纯策略αi∈S1、局中人P2选取纯策略βj∈S2时，则形成对策局势（αi，βj），此时P1获得第k个（k=1，2，…，N）目标的支付值为模糊数a～ijk，而P2相应损失支付值a～ijk，即获得支付值-a～ijk。其中N为局中人P1和P2所考虑的目标个数。为简明，将局中人P1第k个（k=1，2，…，N）目标的支付值可用矩阵直观地表示为

称A～k为局中人P1第k个目标的模糊支付矩阵。

这种支付值模糊、策略集精确的多目标二人零和矩阵对策，简称为模糊多目标二人零和矩阵对策或模糊多目标对策，用表示，其中Γ2N的第1个下标表示有2个局中人，第2个下标表示每个局中人都有N个目标支付值。

2.2考虑局中人偏好信息的模糊多目标二人零和

矩阵对策

假定双方对多目标有相同偏好信息，即局中人P1和P2有相同权重向量w=（w1，w2，…，wN）T，且满足条件

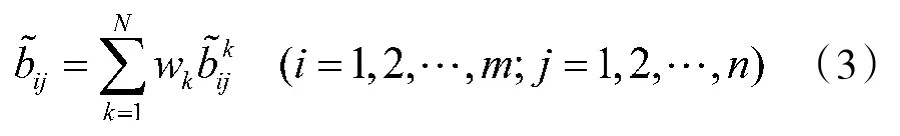
2.3基于λ均值面积排序的模糊线性规划求解

求解模糊矩阵对策的关键是选择合适的方法来比较各个模糊数的大小。为不失一般性，不妨假定所有的模糊数均为三角形模糊数局中人P1希望选取最优策略x*，使得赢得尽可能大于υ；局中人P2希望选取最优策略y*，使得赢得尽可能大于ω。可将问题转化为求解下式的模糊线性规划的最优解，即

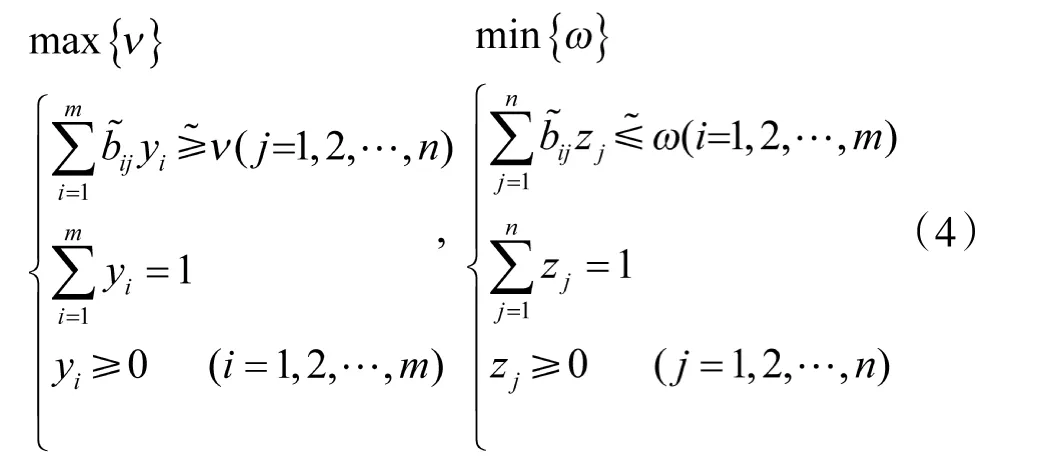
式中“≥～”表示“模糊不小于”，“≤～”表示“模糊不大于”。做变换ui=yi/υ，vj=zj/ω，将模糊规划（4）转化为

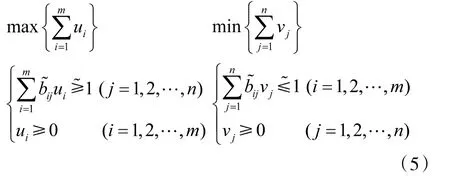
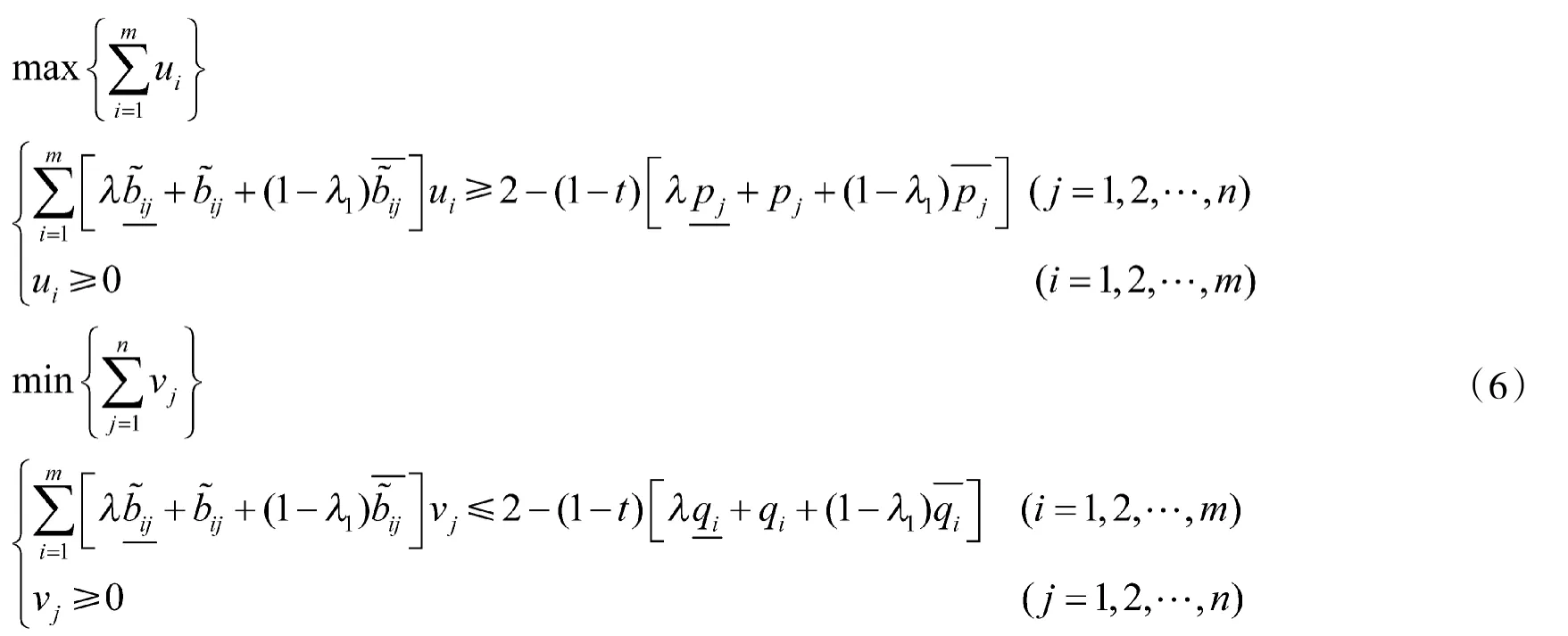
式中，λ∈［0，1］体现局中人对风险的厌恶程度，p～j和q～i表示“几乎为0”的正模糊数，参数t∈［0，1］。

求解线性规划（6），通过变换可得到最优混合策略x*和y*。

3算例分析

参考文献［6-7］，通过定量计算和定性分析相结合，利用式计算反干扰效能支付值，可以得到5项指标的模糊支付矩阵A～k。

对相对自卫距离、抗欺骗式干扰有效概率2项效益型指标，目标相对优属度可选取为

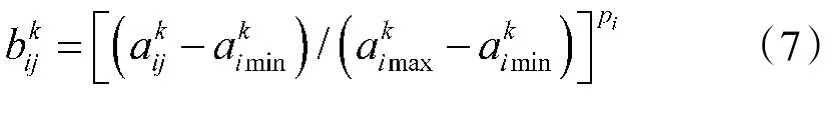
对相对测量精度、雷达观察扇面损失度、系统平均错误航迹数3项成本型指标，目标相对优属度可选取为

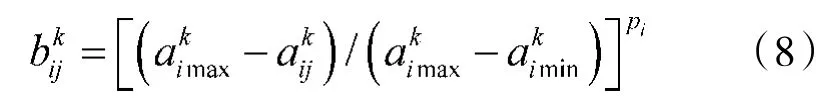
式中，pi是决策者确定的参数，且

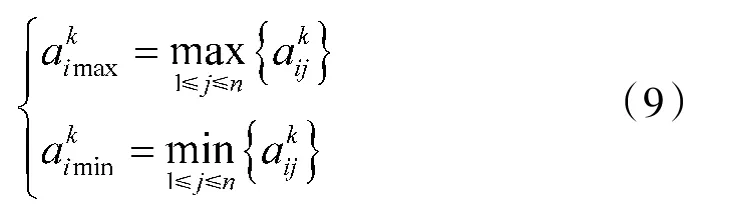
最终得到目标相对优属度矩阵B～k如下页表1～表5所示。通过层次分析法对某型雷达具体分析求解，可以得到总的权重为w=（0.4，0.12，0.18，0.15，0.15）T，利用式（2）得综合值矩阵B～如第88页表6所示。

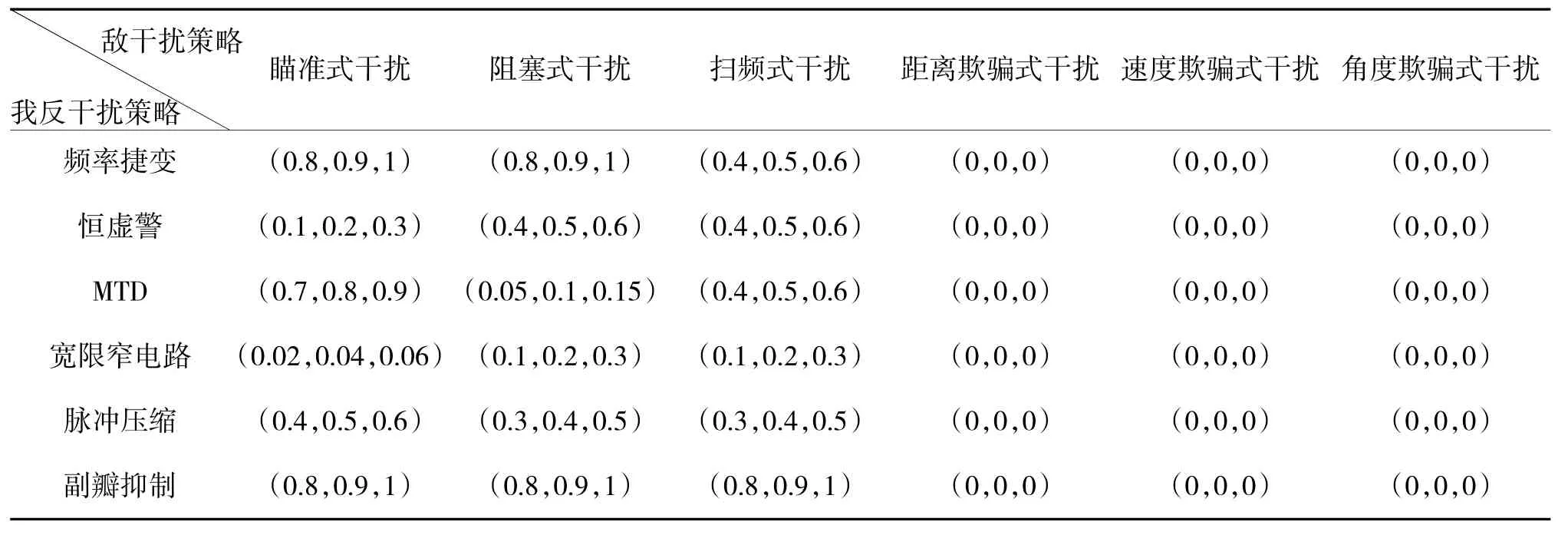
表1　相对自卫距离的目标相对优属度矩阵?

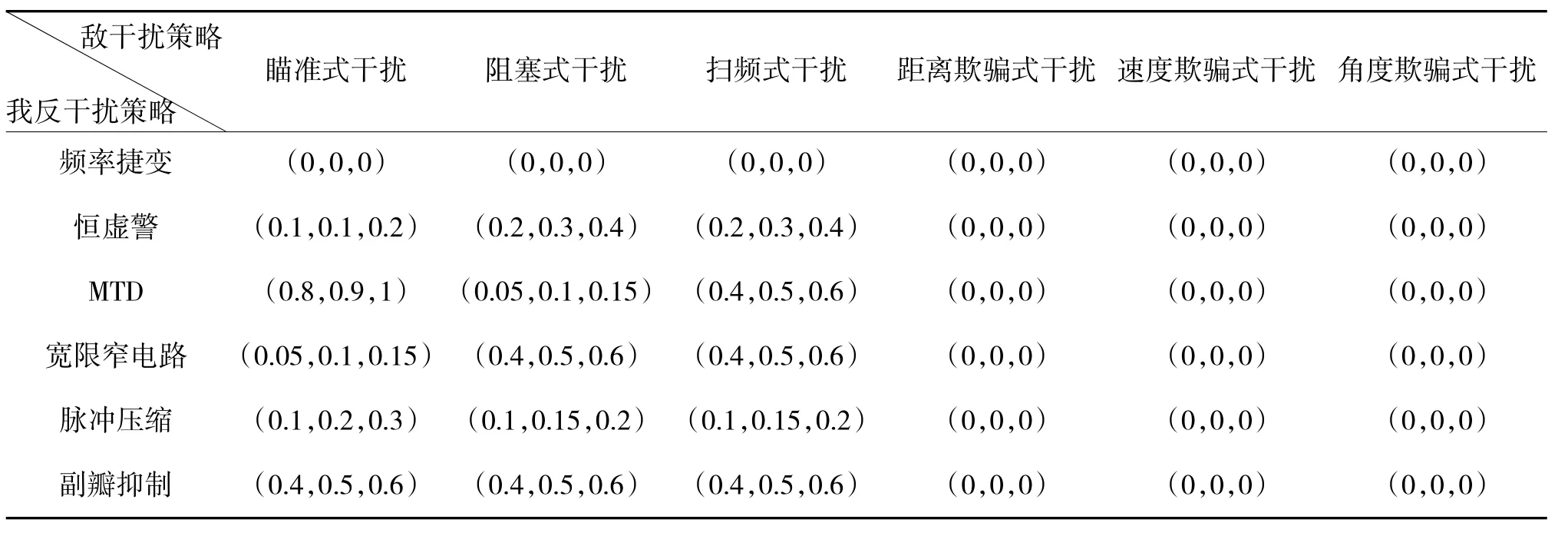
表2　相对测量精度的目标相对优属度矩阵?

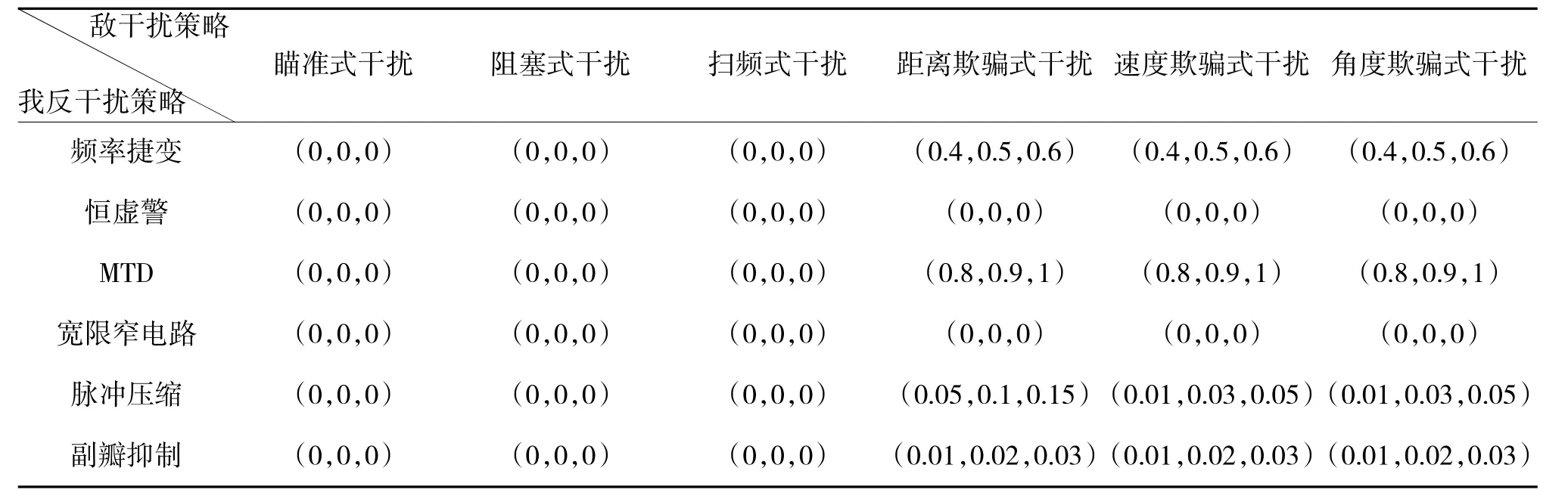
表3　抗欺骗式干扰有效概率的目标相对优属度矩阵?

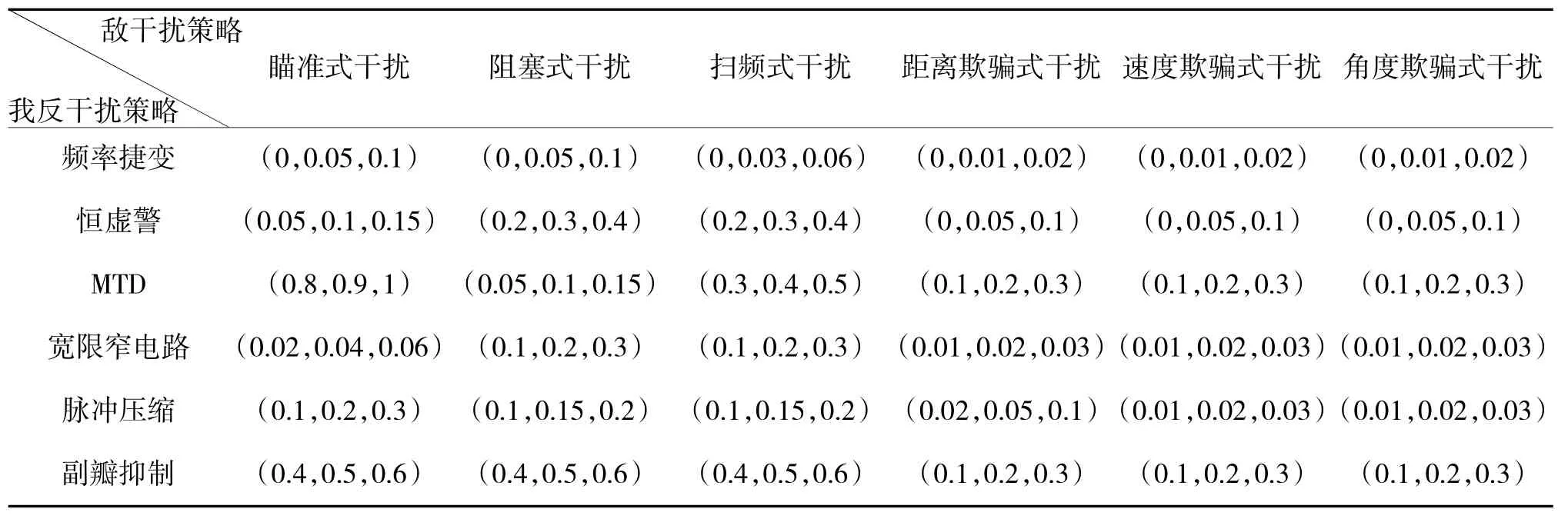
表4　雷达观察扇面损失度的目标相对优属度矩阵?

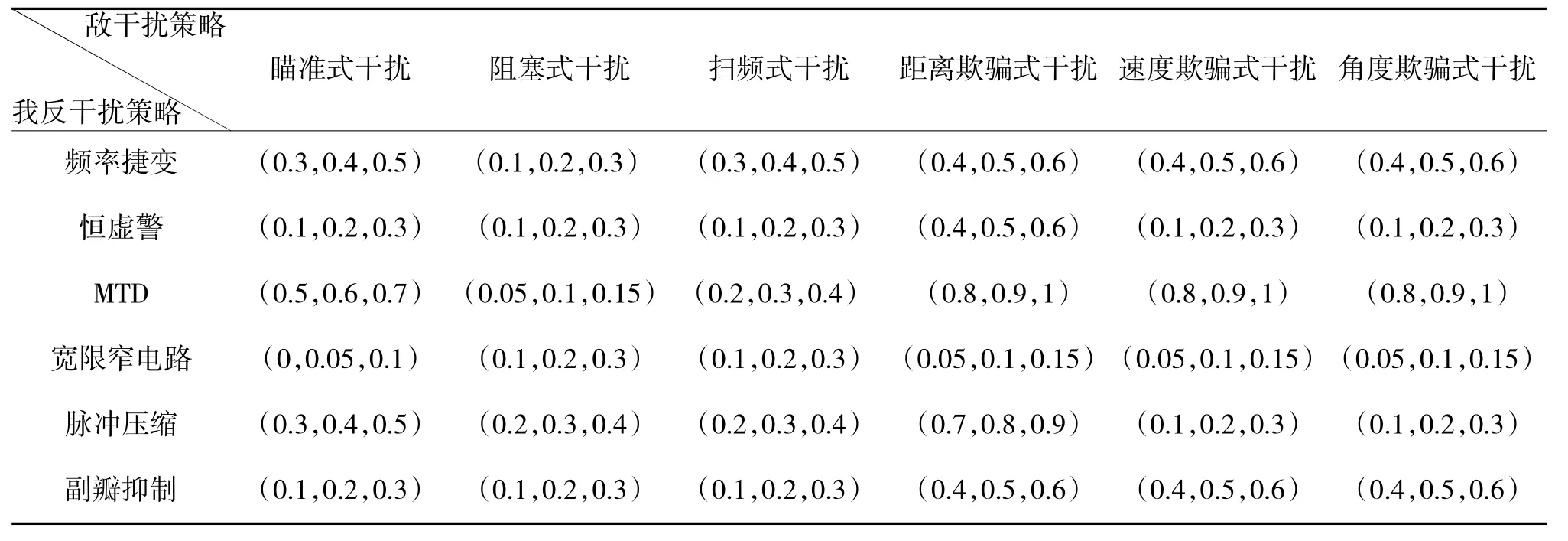
表5　系统平均错误航迹数的目标相对优属度矩阵?

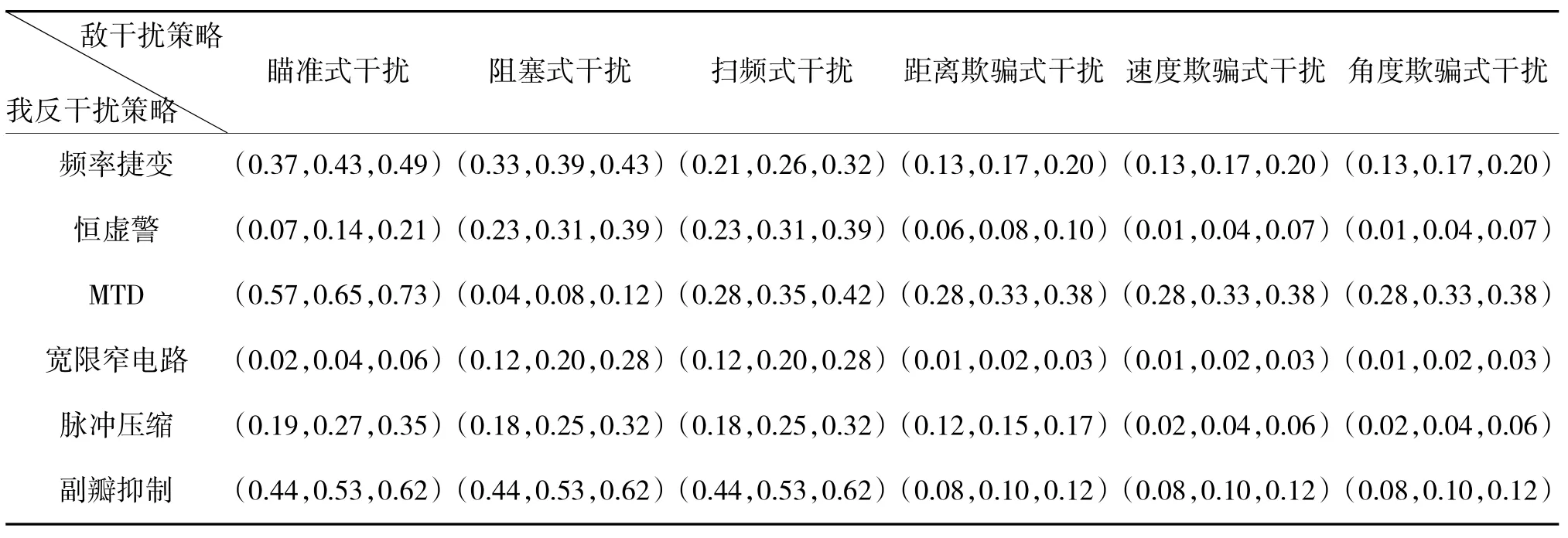
表6　综合值矩阵?

取对风险厌恶程度λ=0.25，p～j=q～i=（0.02，0.03，0.04），对式（5）求解可得：

x*=（0，0，0.632 4，0，0，0.367 6）T

y*=（0，0.338 2，0，0.179 5，0.241 1，0.241 1）T

υ=w=0.245 4

因此，敌方干扰的最优混合策略是分别以33.82 ％，17.95 ％，24.11 ％，24.11 ％的概率，采用阻塞式干扰、距离欺骗式干扰、速度欺骗式干扰和角度欺骗式干扰策略来干扰我方雷达。我方反干扰的最佳混合策略是分别以63.24 ％和36.76 ％的概率，采用MTD和副瓣抑制反干扰。

4　结论

本文根据实际作战中单部雷达对反干扰指标存在偏好、效能指标模糊的情况，建立雷达反干扰策略优化模型，从反压制式干扰、反欺骗式干扰、视频显示三方面建立评估指标体系，解决了其存在局中人偏好、模糊多目标的对策问题。但是分析的雷达干扰和反干扰策略并不全面，所用到的数据并不是实测数据，为了使雷达反干扰策略优化更加准确，需要设计典型的真实对抗试验，以此为样本逐步修正模型参数。

［1］POSTOL T.Field manual FM 3-36 electronic warfare［M］.New York：Department of the Army，2012.

［2］NISHIZAKI I，SAKAWA M.Solutions based on fuzzy goals in fuzzy linear programming games［J］.Fuzzy Sets and Systems，2000，115（1）:105-119.

［3］王天虹，瞿勇，宋业新，等.具有策略偏好的模糊双矩阵对策模型及其运用［J］.火力与指挥控制，2011，36（9）：51-54.

［4］易咸煜，孙闽红，唐斌.基于TOPSIS法的雷达抗干扰措施优化选取［J］.现代雷达，2009，31（10）:35-37.

［5］瞿勇，宋业新，张建军.一类模糊多目标双矩阵对策的粒子群优化算法［J］.海军工程大学学报，2009，21（3）:6-11.

［6］SKOLNIK M.雷达手册［M］.北京:电子工业出版社，2010.

［7］CLARKE J，SUBRAMANIAN A K.A Game Theory approach to ECCM evaluation［C］//IEEE，Inter，Radar Conf，1985.

Optimization of Radar Counter-countermeasure Strategy Based on Fuzzy Multiobjective Games

ZHAI Xiang，JIA Ren-yao，WEI Yuan
（Electronic Engineering Institute，Hefei 230037，China）

Abstract：Considering the difficulties of diversity，fuzzy and multi-weight in the process of countercountermeasure effectiveness evaluation for a single radar，this paper proposes a novel model optimized for counter-countermeasure strategy.Also，based on preference information of players，an optimized and mixed strategy algorithm is designed to find out a better radar anti-interference as well as to offer effective reference for battlefield.

Key words：fuzzy multiobjective games，ECCM，strategy optimization

作者简介：翟翔（1991-），男，江苏南京人，硕士研究生。研究方向：作战运用运筹分析。

收稿日期：2015-03-15修回日期：2015-05-27

文章编号：1002-0640（2016）03-0084-05

中图分类号：O225

文献标识码：A