固体套筒内爆非冲击压缩研究*
杨 龙,李 平,王刚华,阚明先
(中国工程物理研究院流体物理研究所,四川绵阳 621999)
1 引 言
目前,随着脉冲功率技术的快速发展,Z箍缩上的金属固体套筒研究也得到了快速发展,而固体套筒的非冲击压缩研究作为其中一个分支也引起了国内外学者专家的重视。套筒上的非冲击压缩技术[1-2]或斜波加载技术是指,控制样品上的加载压力,即对通过负载的电流进行波形调节,使样品在加载的过程中不出现冲击波,样品的熵增或温升较小。金属固体套筒非冲击加载的概念不同于以往的圆柱套筒冲击波加载概念[3]。冲击波加载实验中,由于冲击加热和套筒电导率的降低,圆柱套筒变成了一个等离子体壳。而在非冲击加载下,套筒就变成了一个热的等离子体外壳推一个相对较冷但电导率更高的内层,这个内层包含有高压缩比的固相物质。2009年,Sandia实验室基于套筒的非冲击压缩提出了磁化套筒惯性聚变(Magnetized Liner Inertial Fusion,MagLIF)概念[4-5],用一个脉冲电流来驱动一个原始状态为固体的圆柱套筒,固体套筒内部填充预先磁化的氘氚(DT)气体燃料,再利用激光将燃料预加热,最后利用准等熵压缩的固体套筒对燃料进行内爆压缩。经校验的2D LASNEX程序模拟表明,如果在内爆时刻有充足的固相套筒物质存在,则当DT燃料耗尽时可以在一些加速器上得到有效的聚变产额,Z装置上25 MA可以实现产额100 kJ,而更高驱动能力的60 MA装置上可以实现超过50 MJ的产额[6-7]。在Sandia实验室的Z装置上进行的厚度为0.9 mm、半径为2.9 mm的Be套筒非冲击加载内爆实验中,当驱动电流的上升时间为300 ns、峰值电流为20 MA时,测量得到的最大内爆压力高达550 GPa,内爆速度超过50 km/s[8]。因此,Z箍缩驱动的非冲击加载实验在材料的高压off-Hugoniot状态测量方面有很大的应用前景。
我们的最终目标是设计一个实验,在给定的电流下,利用非冲击加载技术把金属套筒压缩到可能的最大密度。实验设计基于MDSC磁流体模拟程序,要在模拟中,使金属套筒在磁压力的作用下沿着它的非冲击压缩线压缩。因此,首先需要设计非冲击压缩的电流波形。本研究利用PTS装置shot37丝阵内爆负载电流波形作为MDSC程序的初始输入电流,以此来了解设计金属套筒非冲击压缩中的一些限制。
MDSC模拟程序是流体物理研究所开发的磁流体程序[9-10],采用合理的金属电阻率模型[11],目前已用于流体物理研究所的Z箍缩的丝阵和套筒内爆研究[12],以及磁驱动飞片研究[13-14]。该程序考虑了热扩散、焦耳加热、磁扩散等物理过程,是二维的辐射磁流体力学模拟程序。
2 套筒尺寸设计的限制因素
2.1 冲击波
假设流经套筒表面的电流I在初期是均匀分布的,则磁压力p通过(1)式得到
(1)

图1 冲击波转变位置示意图Fig.1 Time versus Lagrangian coordinate x for wave propagating through the initial state
式中:t为时间,R为套筒外半径,μ0是真空磁导率。此时,磁压力只作用于套筒表面,磁压力驱动的压缩波在套筒样品中以拉格朗日声速C(ρ0)传播;而后来的压缩波扰动则在已经压缩过的套筒介质中传播,其传播速度不再是声速,而是逐渐加快的,这样下来,压缩波剖面的前沿越来越陡,可能会形成冲击波,此时压缩波传播的速度叫欧拉声速C(ρn)。当套筒内部形成冲击波时,材料的压缩就会偏离准等熵加载曲线,得不到高密度的固态物质。磁压力驱动的压缩波变成冲击波需要时间,假设在套筒自由面压力达到最大时(设为τr,即电流脉冲的上升时间),加载面上的扰动赶上t=0时刻的扰动,压缩波转变成冲击波,如图1所示,此时的声速为C(ρmax),则由压缩波转变为冲击波的距离D为[15]
(2)
对于厚度大于D的样品,磁压力会在样品中形成冲击波,所以在样品设计时,要求厚度小于D。
2.2 磁扩散[15]
电流流经套筒表面时,产生的磁扩散波会向样品内部传播,磁扩散波经过的地方会产生焦耳热。设样品的电导率为σ,由Maxwell方程组和欧姆定律可以得出,在磁雷诺数Rm≪1的情况下,样品中的磁场B随时间变化的方程为
∂B/∂t=νm2B
(3)
式中:νm=(σμ0)-1为磁扩散系数。(3)式表明,磁场在导体中的时空变化是一种扩散行为,由磁场扩散方程控制。取二维柱坐标系,则由(3)式可以解得
(4)
由(4)式可知,随着时间的变化,磁场向r方向传播,设磁扩散深度为L,则磁场扩散L深度的时间尺度τd为
τd≈L2/νm=σμ0L2
(5)
(5)式为磁扩散时间和磁扩散深度的定量关系。令脉冲电流上升时间τr=τd,则在实际设计时,应使样品厚度大于L,以保证在电流达到最大时,磁扩散波的前沿仍未到达样品自由面。磁扩散波速度vdiff为
(6)
可见,磁扩散速度和样品的电导率、磁导率有关,电导率越高则磁扩散速度越慢。磁扩散和焦耳加热导致套筒固态部分的可探测厚度减少,因此在给定的电流脉冲下,磁扩散和焦耳加热对套筒有一个最小厚度限制。
3 套筒参数选取及模拟结果
3.1 套筒参数选取范围
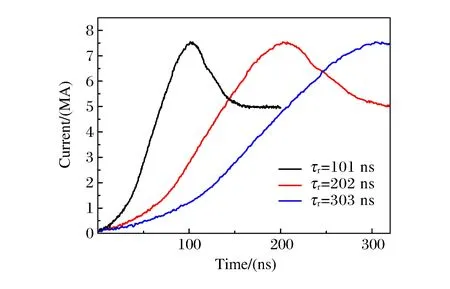
图2 3种上升时间的电流曲线,τr=101 ns 为原始负载电流,τr=202和303 ns 为整形后的负载电流波形Fig.2 Three representative load current pulses.The initial load current is τr=101 ns,while the shaped pulses are τr=202 and 303 ns
方程(2)式和(6)式为电流驱动的非冲击压缩套筒尺寸提供了一系列的量级关系。为了在预设的上升时间内达到一个高的磁驱动非冲击压缩度,由(2)式可知,压缩波向冲击波转变的距离越大越好,因此选择一种有较大欧拉声速的材料比较合适;从(6)式来看,磁扩散速度越慢越好,因此一种有较大电导率的材料比较合适,金属铝则有合适的欧拉声速和电导率。PTS装置shot37的负载电流上升时间为100 ns,由(2)式可知,样品的冲击波转变位置约为1 mm。因此样品的厚度不能大于1 mm,否则可能会有冲击波产生。铝的电导率为35.36 MS/m,真空磁导率μ0=4π×10-7H/m,由(6)式可知,铝样品的磁扩散速度为1.2 km/s,因此样品的厚度不能小于0.12 mm,否则会被电流烧蚀为等离子体。设样品厚度为d,外半径为R,径厚比A=R/d,而A的取值一般在10以内[4],因此可由样品的厚度估算出样品半径的量级。上述分析为样品尺寸的选取提供了一个粗估的量级关系,可以作为MDSC模拟程序的初始值,而具体样品尺寸和电流的选取则需要根据模拟程序的模拟结果。
虽然磁瑞利-泰勒(Magneto-Rayleigh-Taylor,MRT)不稳性会对套筒产生影响[16],但考虑到现在研究的是理想情况下的行为,故此处没有考虑MRT不稳定性。程序的网格尺寸在r和z方向均为30 μm,计算的初始时间步长为0.01 ns,时间步长随着计算的需求而变化。程序的状态方程库采用Sesame数据库,输入电流以PTS shot37的负载电流波形为基础电流,如图2所示。
3.2 冲击压缩
原始PTS shot37负载电流的上升时间为100 ns,由3.1节的分析可知,铝样品的厚度在0.12~1.00 mm之间,此处取厚度d=0.6 mm,半径R=2.5 mm,考虑到电流的驱动能力,取套筒高度h=12 mm,得到自由面速度和自由面磁场强度随时间的变化图(见图3)、密度剖面图(见图4)及压力剖面图(见图5)。

图3 套筒内层速度和磁场强度随时间的变化Fig.3 Velcocity and magnetic field intensity of liner inner surface versus time
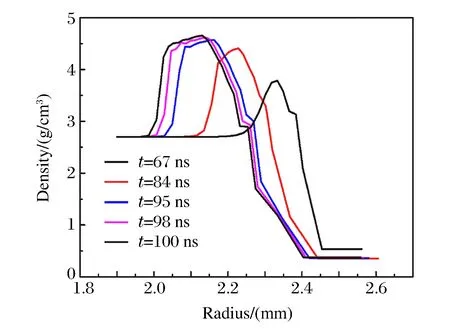
图4 不同时刻套筒的密度剖面图Fig.4 Radial density profiles at 5 different times

图5 不同时刻套筒的压力剖面图Fig.5 Radial pressure profiles at 5 different times
从图3可以看出,峰值电流处套筒内层的磁场强度为零,故可以认为0.6 mm厚度满足磁扩散的要求。从图4和图5可以看出,在67 ns之前,套筒物质的密度和压力变化较平缓,密度波形前沿在0.1 mm距离内下降了1.0 g/cm3;而在67 ns 之后,密度和压力剖面前沿均出现斜率迅速增大的趋势,密度剖面在0.03 mm距离内下降了1.8 g/cm3,通常认为这就是冲击波。因此,0.6 mm 的参考厚度并不满足无冲击的要求,这个厚度是过大的,故调整套筒的厚度,结果如表1所示。其中:tdiff为磁扩散到达自由面的时间,当自由面的磁场强度大于10-4T时认为磁扩散到达自由面,记录前一时刻的时间为tdiff;tD是冲击波发生的时刻;“—”表示没有有效数据。

表1 原始负载电流下的计算结果Table 1 Calculation results with initial load current

图6 套筒内层速度和磁场强度随时间的变化(d=0.2 mm,R=2.0 mm)Fig.6 Velcocity and magnetic field intensity of liner inner surface versus time with d=0.2 mm,R=2.0 mm
从表1可以看出,当套筒厚度大于0.35 mm时,套筒在运动过程中,其内部有冲击波产生,如算例No.1~No.7所示;而从算例No.9~No.15可以看出,当套筒厚度小于0.4 mm时,虽然在电流上升时间(100 ns)以内,套筒内的压缩波不会转变成冲击波,但磁场会在电流脉冲达到最大值之前扩散至套筒内层。为了更清楚地呈现套筒内磁场强度的变化情况,做出算例No.15中厚度为0.2 mm、半径为2.0 mm的套筒内层速度和套筒内层磁场强度随时间变化的关系图,如图6所示。由图6可以看到,磁场在60 ns时便扩散至自由面。因此,在原始电流曲线下,并不能得到一个合适的套筒尺寸,让套筒在运动过程中实现磁场的无冲击压缩。
3.3 非冲击压缩
为得到上升时间更长的电流脉冲,对电流脉冲进行波形调节。由于本研究主要目的是不让套筒中形成冲击波,并未设定需要达到的压力值,所以仅改变脉冲电流的上升时间,而不改变其波形,然后通过数值模拟观察在这些上升时间内是否存在合适的套筒尺寸可实现磁场的无冲击压缩。把原始脉冲电流的上升时间从101 ns分别调节为202和303 ns,输入电流曲线如图2所示。由3.1节的分析可知,当τr=202 ns时,套筒内磁扩散的深度为0.22 mm,冲击波的转变位置为2 mm;当τr=303 ns时,套筒内磁扩散的深度为0.33 mm,冲击波的转变位置为3 mm。记录下202和303 ns时刻各种套筒尺寸下磁扩散到达套筒内层的时间tdiff和套筒内部冲击波发生的时刻tD,以及套筒的碰轴时刻tA,如表2所示。算例No.1~No.5为τr=202 ns的结果,其中No.2~No.5固定套筒半径不变。算例No.6~No.24为τr=303 ns的结果,其中No.6~No.8固定套筒半径为3.0 mm,改变套筒厚度;No.9~No.16固定套筒半径为2.5 mm,改变套筒厚度;No.18~No.24固定套筒厚度为0.6 mm,改变套筒半径;算例No.17为No.14的对照。
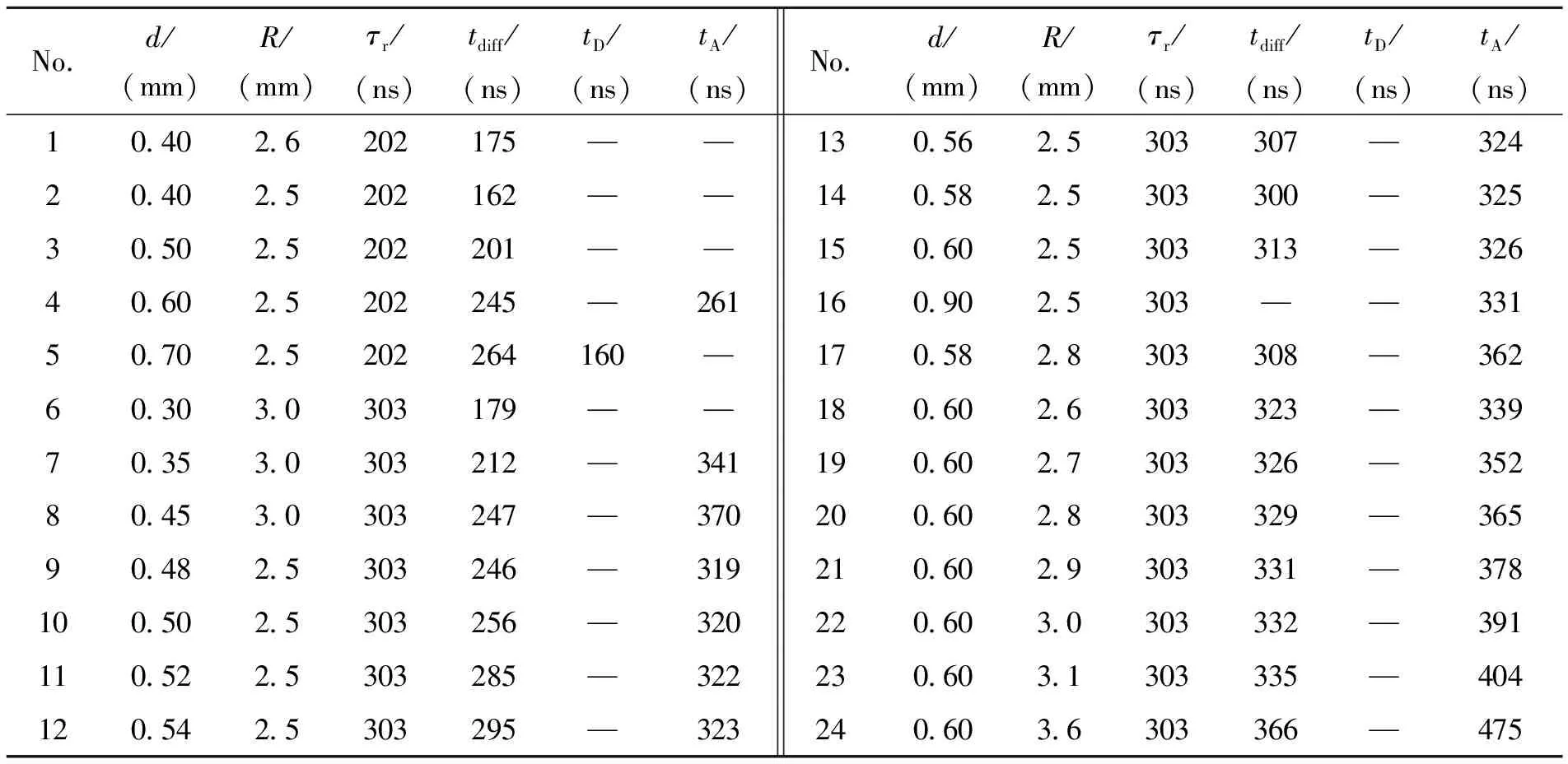
表2 电流整形之后的计算结果Table 2 Calculation results with shaped load current
从上面的分析可知,当电流上升时间为303 ns时,预估的满足要求的套筒厚度范围为0.33~3.00 mm。结合表2算例No.16可以看出,对于0.90 mm的厚度,套筒在运动的过程中没有形成冲击波,但是此时电流已经无法驱动这样的套筒,其碰轴速度和压力值很小,因此对303 ns的电流上升时间,其合适的套筒厚度范围缩小为0.33~0.90 mm,而对于上升时间为202 ns的脉冲电流,其相应的厚度为0.22~0.70 mm。我们的优化分析正是在这个范围内取值,从而得到表2。
此处用碰轴时间来表征从负载电流中获得的压力,在非冲击压缩中,压力做功直接转化为系统的动能,因此压力越大,速度越快,越早碰轴。从表2可以看出,套筒的碰轴时间和半径相关,而对套筒厚度的变化不敏感。算例No.9~No.15中,套筒半径固定为2.5 mm,套筒厚度从0.48 mm变化到0.60 mm,其碰轴时间为319~326 ns,变化很小。因此可以得出这样一种关系,套筒的碰轴时间是和半径相关的量,一旦确定一个电流上升时间,就可以通过模拟程序得到和该电流上升时间相匹配的套筒半径,使套筒在电流值最大时碰轴。当电流上升时间τr=303 ns时,半径为2.5 mm的套筒的碰轴时间在320 ns附近,如果要求在303 ns时碰轴,那么套筒半径应小于2.5 mm。同理,对于τr=202 ns,如算例No.4所示,半径为2.5 mm的套筒的碰轴时间为261 ns,如果要求碰轴时间和电流上升时间相匹配,其设计半径也要小于2.5 mm。
磁扩散深度和套筒的厚度相关,在算例No.18~No.24中,套筒厚度固定为0.6 mm,套筒半径从2.6 mm变化到3.6 mm,磁扩散到达套筒自由面的时间为323~366 ns,随着半径的增加而缓慢变化。因此当电流上升时间确定时,可以认为磁扩散深度是一个仅和套筒厚度相关的量。从算例No.14、No.15、No.17中可以看出,当脉冲电流上升时间为303 ns时,如果要求在303 ns时磁扩散刚好到达套筒自由面,则套筒厚度应在0.58~0.60 mm之间;但是实际上套筒在碰轴时能够保留的固相物质越多越好,因此结合前文的分析,进一步将合适的套筒厚度范围缩小至0.58~0.90 mm。同理,当电流的上升时间为202 ns时,从表2算例No.2~No.4可以看出,其符合要求的套筒厚度为0.5~0.7 mm。
至此,通过表2得出了套筒在电流上升时间为202和303 ns下的无冲击压缩厚度和半径范围。下面通过解析算例No.15的套筒在运动过程中的压力剖面和密度剖面,观察其尺寸是否满足无冲击压缩的要求。套筒厚度为0.6 mm,半径为2.5 mm,选取200、214、270、280、290 ns时刻,做其密度剖面图(见图7)和压力剖面图(见图8)。由图7、图8发现,密度和压力剖面前沿都是连续变化的,和冲击压缩情况的图4、图5区别明显。在326 ns时刻,套筒内层达到设定的z轴,发生碰撞,该过程中,自由面的最大速度达到15 km/s,如图9所示。图10为套筒表面的磁压力随时间变化的历史,即厚0.6 mm、半径为2.5 mm的套筒的无冲击波加载压力曲线。
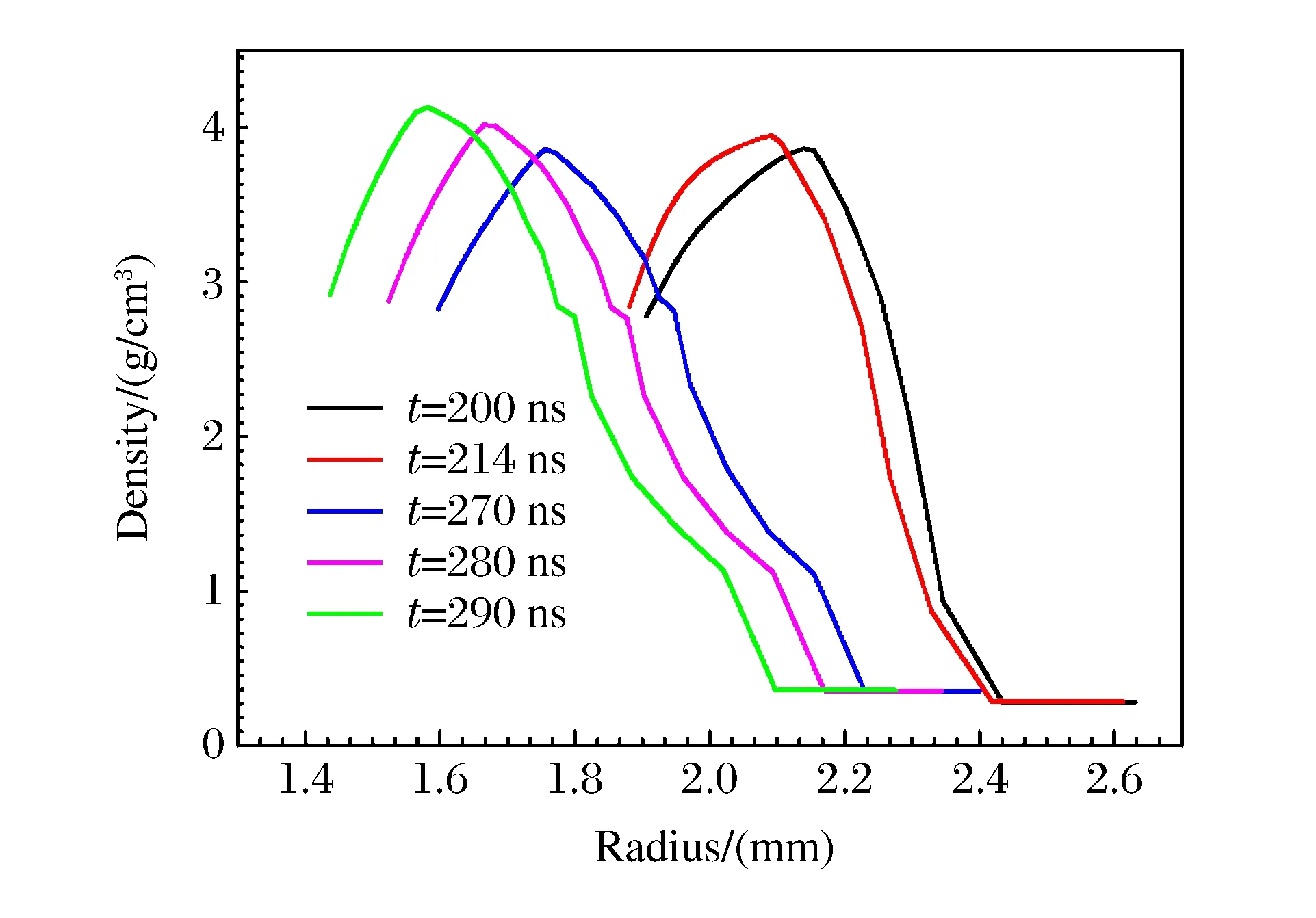
图7 不同时刻套筒的密度剖面Fig.7 Radial density profiles at 5 different times
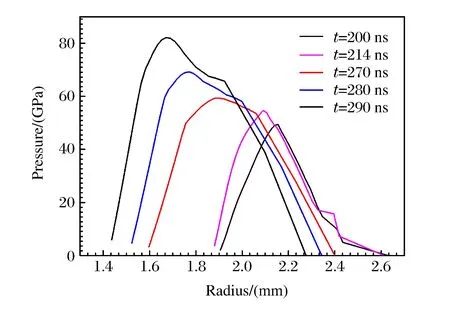
图8 不同时刻套筒的压力剖面Fig.8 Radial pressure profiles at 5 different times
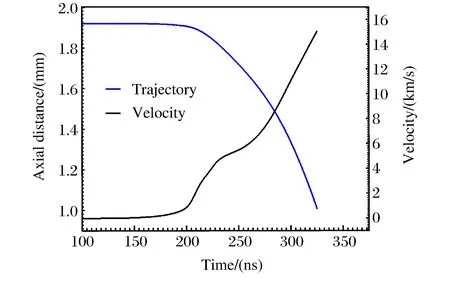
图9 套筒内层速度及运动路径历史Fig.9 Velocity and trajectory of liner inner surface versus time
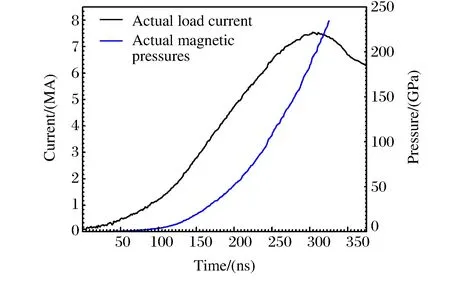
图10 套筒表面的加载电流和磁压力随时间变化的历史Fig.10 Actual load current and actual magnetic pressures versus time
3.4 套筒内部物质状态的判断
为了验证套筒在最大脉冲电流时刻确实存在固相,需要判断套筒内部物质的状态,我们根据铝的高压熔化曲线[17]进行判断。首先提取套筒网格点的压力(p)和温度(T),然后将其和铝的熔化曲线做比较,若在曲线之上,则认为是液相,若在曲线之下则认为是固相。算例No.17中,套筒在300 ns时的密度和压力如图11所示,将网格点的p-T关系和铝的熔化曲线绘制在一张图中,如图12所示,二者的交点为90 GPa、4 000 K,由此可以推算出,套筒的两相分界线在1.5 mm处。
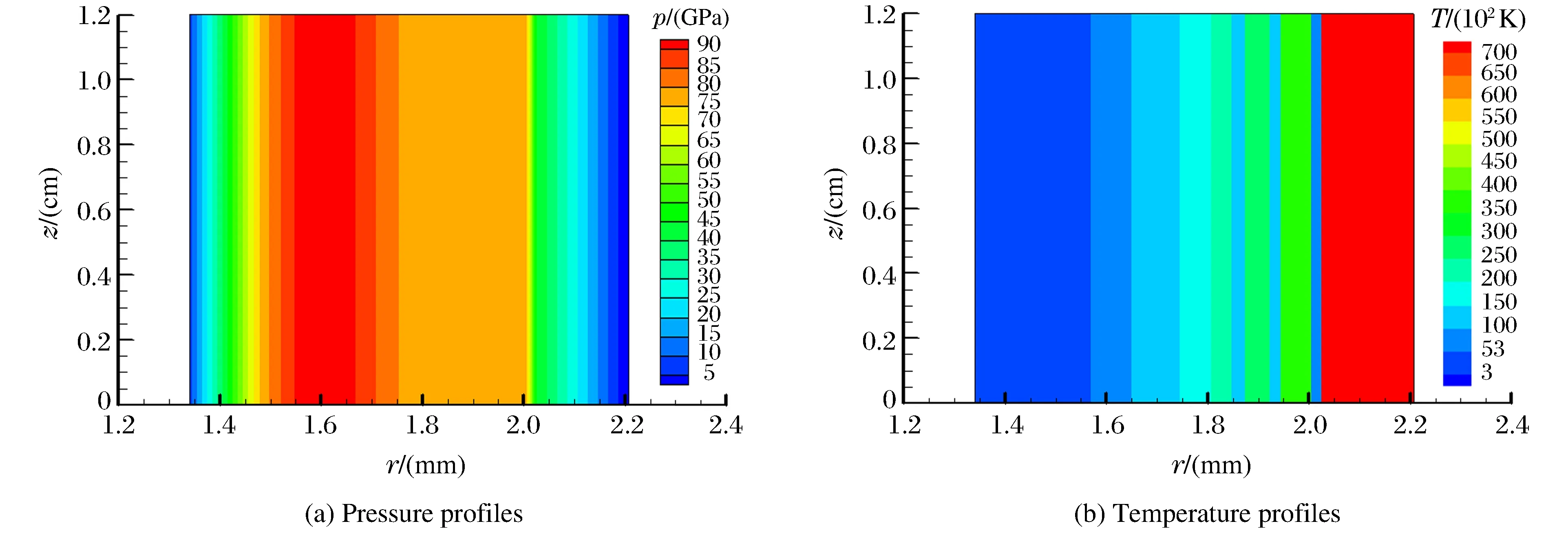
图11 t=300 ns时刻套筒的压力分布图和温度分布图Fig.11 Radial pressure profiles and radial temperature profiles at 300 ns
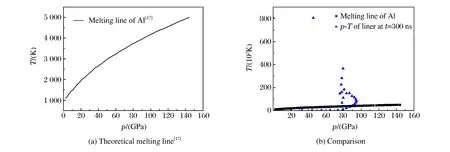
图12 铝的熔化线及其与t=300 ns时刻套筒剖面的压力-温度关系对比Fig.12 Comparison between the theoretical melting line[17] of Al and the liner’s radial p-T relation at t=300 ns
有了上面判断固-液相边界的知识后,下面分析表2中算例No.15在电流最大处所能达到的最大压力及此时的固-液相边界,如图13所示。固-液相边界在1.28 mm处,保留的固态部分的厚度约为 0.12 mm,固相部分内磁场强度为零,说明磁扩散没有到达此区域,这和之前通过铝的熔化曲线得到的结论相吻合,此时固相部分的最大压力值为63 GPa。该固相物质区域会一直保留到碰轴时刻,如图14所示,在t=326 ns碰轴时刻,固相部分的厚度约为0.12 mm。这表明,当电流上升时间为303 ns时,d=0.6 mm、R=2.5 mm的套筒参数可满足无冲击波压缩的要求。

图13 t=303 ns时刻套筒的密度、压力、磁场强度剖面以及此刻的相图Fig.13 Liner radial density,pressure and magnetic pressure profiles and the phase diagram at t=303 ns
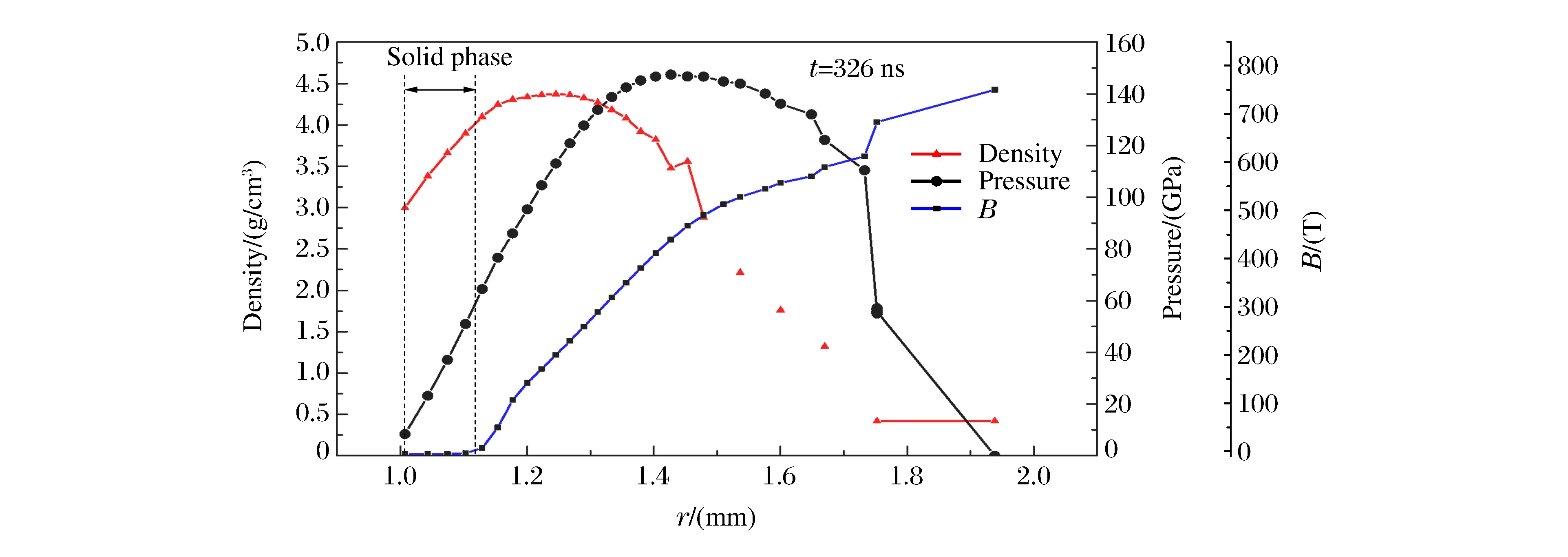
图14 t=326 ns时刻套筒的密度、压力、磁场强度剖面以及此刻的相图Fig.14 Liner radial density,pressure and magnetic pressure profiles and the phase diagram at t=326 ns
4 结 论
通过MDSC程序,成功表现出了厚靶套筒的冲击压缩现象和非冲击压缩现象。在以PTS shot37负载电流为参考电流的情况下,通过MDSC程序模拟得出,原始负载电流下,没有合适的套筒尺寸实现无冲击压缩。对原始电流进行波形调节后得出,要实现非冲击压缩,当电流上升时间为202 ns时,套筒厚度应在0.50~0.70 mm之间,半径应小于2.5 mm;当电流上升时间为303 ns时,套筒厚度应大于0.58 mm,半径应小于2.5 mm。当电流上升时间为303 ns,套筒半径为2.5 mm、厚0.6 mm时,套筒在最大电流处能够获得最大压力值为63 GPa,此时固相物质厚度约为0.12 mm,一直保留至发生碰轴。套筒的最大内爆速度为15 km/s。
[1] SAVAGE M,BENNETT L,BLISS D,et al.An overview of pulse compression and power flow in the upgradedZpulsed power driver [C]//2007 IEEE Pulsed Power Plasma Science Conference.Albuquerque,NM:IEEE,2007:979-984.
[2] MATZEN M K,SWEENEY M A,ADAMS R G,et al.Pulsed-power-driven high energy density physics and inertial confinement fusion research [J].Phys Plasmas,2005,12(5):055503.
[3] SINARS D B,SLUTZ S A,HERRMANN M C,et al.Measurements of magneto-Rayleigh-Taylor instability growth during the implosion of initially solid metal liners [J].Phys Plasmas,2011,18(5):056301.
[4] SLUTZ S A,HERRMANN M C,VESEY R A,et al.Pulsed-power-driven cylindrical liner implosions of laser preheated fuel magnetized with an axial field [J].Phys Plasmas,2010,17:056303.
[5] SLUTZ S A,VESEY R A.High-gain magnetized inertial fusion [J].Phys Rev Lett,2012,108:025003.
[6] MATZEN M K,ATHERTON B W,CUNEO M E.The refurbishedZfacility:capabilities and recent experiments [J].Acta Phys Pol A,2009,115(6):956-958.
[7] ROSE D V,WELCH D R,MADRID E A,et al.Three-dimensional electromagnetic model of the pulsed-powerZ-pinch accelerator [J].Phys Rev ST Accel Beams,2010,13(1):010402.
[8] MCBRIDE R D,MARTIN M R,LEMKE R W,et al.Beryllium liner implosion experiments on theZaccelerator in preparation for magnetized liner inertial fusion [J].Phys Plasmas,2013,20(5):056309.
[9] 阚明先,胡熙静,王刚华.二维磁流体力学ALE数值模拟 [J].高能量密度物理,2009(2):56-60.
KAN M X,HU X J,WANG G H.Two dimensional MHD ALE numerical simulation [J].High Energy Density Physics,2009(2):56-60.
[10] 阚明先,蒋吉昊,王刚华.衬套内爆ALE方法二维MHD数值模拟 [J].四川大学报(自然科学版),2007,44(1):91-96.
KAN M X,JIANG J H,WANG G H.ALE simulation of 2D MHD for liner [J].Journal of Sichuan University (Natural Science Edition),2007,44(1):91-96.
[11] 阚明先,王刚华,赵海龙.金属电阻率模型 [J].爆炸与冲击,2013,33(3):282-286.
KAN M X,WANG G H,ZHAO H L.Electrical resistivity model for metals [J].Explosion and Shock Waves,2013,33(3):282-286.
[12] 王刚华,胡熙静,孙承纬.双层钨衬套Z箍缩内爆数值模拟 [J].高压物理学报,2004,18(4):364-367.
WANG G H,HU X J,SUN C W.Simulation of magneto hydrodynamics for plasma jetting on wire pinch [J].Chinese Journal of High Pressure Physics,2004,18(4):364-367.
[13] 阚明先,王刚华,赵海龙.磁驱动飞片二维磁流体力学数值模拟 [J].强激光与电子束,2013,25(8):2137-2140.
KAN M X,WANG G H,ZHAO H L.Two-dimensional magneto-hydrodynamic simulations of magnetically accelerated flyer plates [J].High Power Laser and Particle Beams,2013,25(8):2137-2140.
[14] 王刚华,孙承纬,赵剑衡.磁驱动平面飞片的一维磁流体力学计算 [J].爆炸与冲击,2008,28(3):261-264.
WANG G H,SUN C W,ZHAO J H.One-dimensional,magneto hydrodynamic simulations of magnetically driven flyer plates [J].Explosion and Shock Waves,2008,28(3):261-264.
[15] 孙承纬.磁驱动等熵压缩和高速飞片的实验技术 [J].爆轰波与冲击波,2005,3(9):125-138.
SUN C W.Research on magnetically driven isentropic compression and high speed flyer plates [J].Detonation and Shock Wave,2005,3(9):125-138.
[16] RYUTOV D D,DERZON M S,MATZEN M K.The physics of fastZpinches [J].Rev Mod Phys,2000,72(1):167-223.