关于稳定t结构的一个注记

孙永亮

(西北民族大学 数学与计算机科学学院,甘肃 兰州 730030)

关于稳定t结构的一个注记

孙永亮

(西北民族大学 数学与计算机科学学院,甘肃 兰州 730030)

文章中考虑了有足够多投射对象的Grothendieck范畴的同伦范畴中的一个稳定t结构及其三角粘和,并给出了稳定t结构的一些性质.

稳定t结构；同伦投射复形；一个注记

0 引言

从文献[1]中的定理4.5.4和4.6.8我们知道，在有足够多投射对象的Grothendieck范畴的同伦范畴中任意复形都有同伦投射和同伦内射分解,并且这种分解在同伦范畴中是惟一的.很自然地我们看到同伦投射复形与正合复形是同伦范畴的两个三角子范畴并且是同伦范畴的一个稳定t结构.

1 预备概念

定义1 设A是Abel范畴.A上的复形P称为同伦投射复形,如果对A上的每个无环复形E,Hom复形Hom(P，E)仍是无环复形或等价的,则HomK(A)(P，E)=0.

定义2 设A是Abel范畴,如果A有正合的正向极限并且还有生成子,则称它为一个Grothendieck范畴.

定义3 三角范畴(D，[1])的一个t结构是D的一对全子范畴(D≤0,D≥0),使得(D≤n：=D≤0[-n]),(D≥n：=D≥0[-n])∀n∈Z,满足下面的条件(t1)、(t2)和(t3):

(t1) HomD(X,Y)=0，∀X∈D≤0,Y∈D≥1.

(t2)D≤0⊂D≤1,D≥1⊂D≥0.

(t3) 对于任意X∈D,存在D中的好三角:A→X→B→A[1],使得A∈D≤0,B∈D≥1.

记号：K(A),Khproj,KE,Khinj分别表示A上的同伦范畴,同伦投射复形范畴,正合复形范畴以及同伦内射复形范畴.

2 本文结论

引理1Khproj,KE,Khinj是K(A)的三角子范畴.

证明 对于Khproj其中(tr1),(tr3)显然.我们证明(tr2)和(tr4).

(tr2) 对于任意的f:X→Y,把它嵌入到一个好三角当中得到：X→Y→Z→X[1]，其中Z≅con(f)≅X[1]⊕Y.显然HomK(A)(Z,E)≅HomK(A)(X[1]，E)⊕HomK(A)(Y，E)≅0.所以Z也是同伦投射的.

(tr4) 显然,我们有K(A)中的一个八面体.由于(tr2)以及K(A)中的(tr4)我们知道(tr4)成立.

同理可知，KE，Khinj也是三角子范畴.

定理1 (Khproj,KE),(KE,Khinj)是K(A)中的稳定t结构,其中A是有足够多投射对象的Grothendieck范畴.

证明 由同伦投射复形的定义可知Homk(A)(Khproj,KE)=0.而在有足够多投射对象的Grothendieck范畴的同伦范畴中任意复形都有惟一的同伦投射分解，即对于任意的X∈K(A)都存在拟同构P→X，其中P∈Khproj.嵌入到好三角中去得到一个好三角P→X→E→P[1].由长序列引理知E∈KE,即任意X∈K(A)的都可以得到一个t分解.因此(Khproj,KE)是K(A)的一个稳定t结构.同理可得(KE,Kinj)也是K(A)的一个稳定t结构.

推论1 在有足够多投射对象的Grothendieck范畴的同伦范畴K(A)中有一个三角粘和:

证明 由稳定t结构与三角粘和的关系直接可得.

我们给出稳定t结构的一些性质.

命题1 设(U,V)三角范畴(T,[1])的稳定t结构, (U1,V1)是三角范畴(T1,[1])的稳定t结构.我们有：

1)若F∶U→U1,G∶V→V1是三角等价,且对于任意u∈U,υ∈V都有同构Sυu∶Hom(υ,u)≅Hom(G(υ),F(u)),则存在一个三角等价,且H∶T→T1,且HU≅F,HV≅G.

2)若F∶T→T1是一个三角等价,且FU∶U→U1是一个三角等价,则FV∶V→V1是一个三角等价.

3)若F∶T→T1是一个三角等价,且FV∶V→V1是一个三角等价,则FU∶U→U1是一个三角等价.

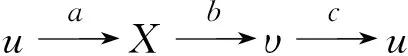
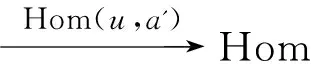
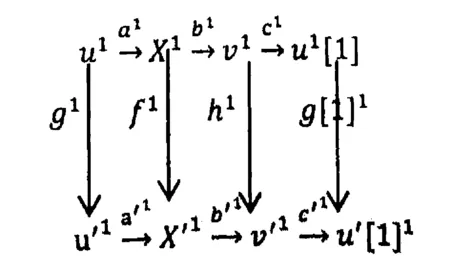
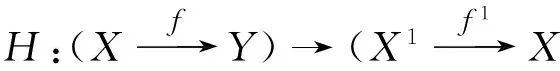
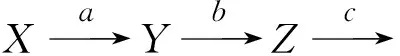
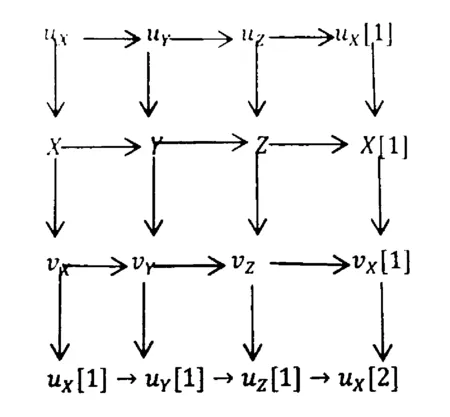
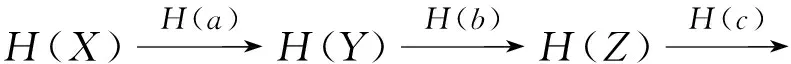
2)由于FU∶U→U1是一个三角等价,以及F本身是一个三角等价.容易知道F诱导了一个三角等价:T/U→T1/U1.又因为有三角等价:T/U≅V和T1/U1≅V1我们知道FVV:→V1是一个三角等价.

3) 类似可证.

命题2 设(U,V)是三角范畴(T，[1])的稳定t结构,且C⊂U,K⊂V是两个三角子范畴，则*运算构成新的三角子范畴且有稳定t结构(C,D)，其中C*D={X∈T|∃}好三角c→X→d→c[1]，使得c∈C,d∈D.

证明 先证明C*D是一个三角范畴,(tr1)显然.对于任意f:X1→X2把它嵌入到T中的一个好三角X1→X2→X→X1[1],由X1,X2的t分解和T中的4×4引理我们知道X∈C*D.(tr3)、(tr4)显然.并且由于C⊂U,D⊂V,显然C*D有稳定t结构(C,D).

[1]章璞. 三角范畴与导出范畴[M]. 北京：科学出版社,2014.

An Annotation about Stable t-structure

SUN Yong-liang

(Mathematics and Computer Science College，Northwest University for Nationalities，Lanzhou 730030, China)

stable t-structure of the homotopy category of Grothendieck category was discussed with enough projective objects in the present article. Some properties of stable t-structure were also provided.

Stable t-structure; Homotopy projective complex

2016-10-11

孙永亮(1992—)，男， 江苏盐城人，硕士研究生，主要从事代数表示论方面的研究.

O153.3

A

1009-2102(2016)04-0008-03