钢轨裂纹疲劳与磨损耦合关系的研究

李孝滔，文良华，李煦，曹世豪，江晓禹

(西南交通大学 力学与工程学院，四川 成都 610031)



钢轨裂纹疲劳与磨损耦合关系的研究

李孝滔，文良华，李煦，曹世豪，江晓禹

(西南交通大学 力学与工程学院，四川 成都 610031)

摘要:采用有限元分析软件ANSYS结合疲劳与磨耗耦合模型，分析钢轨裂纹疲劳与磨损的竞争机制。10 t轴重车轮以纯滚动方式滚过初始长度为100 μm，扩展角度为30°的钢轨表面裂纹，计算出各个阶段的等效应力强度因子K(eff)。研究结果表明，钢轨的破坏形式以疲劳破坏为主；随着裂纹长度增加，其扩展速率先增加后减小，当裂纹长度为600时，其扩展速率最快；在裂纹初始扩展阶段，裂纹扩展方向基本与行车方向一致；当裂纹长度大于600 μm后，裂纹扩展角度超过90°，裂纹沿着与起始阶段相反的方向扩展，形成鱼钩型裂纹。

关键词：ANSYS；疲劳；磨损；耦合；裂纹扩展方向

在铁路运输系统中,钢轨的使用寿命主要由滚动接触疲劳和磨耗共同决定[1-2]。随着我国重载与高速铁路的快速发展，轮轨滚动接触疲劳与磨耗问题变得越来越严重，已成为影响铁路运输安全的重要因素。对于轮轨接触疲劳和磨耗关系，国内外学者进行了大量的研究。钟雯等[3]研究表明，重载时钢轨以磨耗为主；高速时钢轨以疲劳为主。周剑华等[4]研究得出改善轮轨匹配关系使轮轨形成共形接触，合理进行预防性和校正性打磨，严格执行钢轨分级使用规定，可以有效预防和减轻钢轨剥离掉块缺陷的产生。Patel等[5]在Paris公式的基础上，综合考虑钢轨磨耗损失量，得出疲劳与磨耗耦合作用下的裂纹扩展寿命预测模型。因此，开展钢轨接触疲劳和磨耗耦合关系的研究，有助于正确判断钢轨的伤损类型及原因，准确估算钢轨的接触疲劳裂纹的扩展寿命以及最佳打磨磨损率，对于维护高速铁路的安全服役、节约铁路运营成本等具有重要的现实意义。

1理论研究

1.1复合型裂纹疲劳扩展速率

1927年Palaniswamy等[6]将能量理论应用于Ⅰ-Ⅱ复合型裂纹扩展分析，提出了2个假设：裂纹沿着能量释放率最大的方向扩展；当这个方向的能量释放率达到一个临界值时裂纹将扩展。能量释放率G和应力强度因子K在力学上是等价的，因为它们之间有确定的关系[7-8]，如下式：

(1)

式中：E为弹性模量；v是泊松比；K为Ⅰ型或Ⅱ型裂纹的应力强度因子。由于G和K在力学上是等价的，为了后面计算的方便，用K来描述能量释放率理论，即：裂纹沿着应力强度因子K最大的方向扩展；当这个方向的应力强度因子K达到门槛值时裂纹将扩展。

对于Ⅰ-Ⅱ复合型裂纹，有：

(2)

将式(2)写成与式(1)对应的形式：

(3)

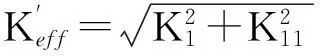
(4)

可以令：

Keff=K1+K11

(5)

式(5)是工程上经常采用的Ⅰ-Ⅱ复合型判据。可以看到，式(5)没有改变KI和KII的相对关系，它们在这个式子中处于平等地位，而且这个判据相对偏安全，因此工程上经常采用[9]，后面的计算也将采用这一判据。

裂纹扩展速率可由Paris公式求得，如式(6)所示[10]。

(6)

式中，da/dN是循环荷载每作用一次裂纹的扩展速率；C和m主要由材料所确定的常数；△K是应力强度因子幅值，可由式(7)求得。

ΔK=Kmax-Kmin

(7)

1.2疲劳与磨耗的耦合作用

钢轨的损伤主要有磨损和疲劳两种形式，由于磨损与滚动接触疲劳是不可分离的两种损伤形式，因此它们之间存在一定的相互作用。Patel等[5]在Paris公式的基础上给出了单个裂纹扩展速率和表面磨损率之间的关系(式(8))，其模型的示意图，如图1。

(8)

式中： da/dN为载荷单位循环作用下裂纹净扩展长度；w/sinθ为载荷作用时因表面材料磨损导致裂纹长度被截断的速率；w为载荷单位循环作用下的磨损率；θ为裂纹和行车方向间的夹角。分析可知，滚动磨损过程中，磨损对疲劳裂纹扩展具有一定的抑制和阻碍作用，即如果裂纹尖端扩展速率大于因表面材料磨损对裂纹根部的截断率，则疲劳裂纹将继续扩展；反之，裂纹长度将随磨损的进行不断缩短，直至裂纹彻底被磨掉。

图1　磨损率与裂纹尖端扩展速率关系模型Fig.1 Model of relationship between wear rate and crack growth rate

铁路钢轨滚动疲劳损伤和磨损之间存在着相互竞争与制约的耦合作用关系，这主要表现为磨损严重时，疲劳损伤往往较轻；而疲劳损伤严重时，磨损相对轻微。实际中，裂纹扩展速率与钢轨材料磨损率的关系主要表现为，若裂纹的扩展速率大于钢轨材料的磨损率，那么钢轨材料的疲劳损伤对钢轨的失效就占据主导地位；相反，若钢轨材料的磨损率大于钢轨材料裂纹的扩展速率，那么钢轨材料的磨损对钢轨失效就占主导地位，因此只有裂纹扩展速率与材料的磨损率达到平衡时才能最大限度地延长钢轨的使用寿命。

1.3钢轨表面裂纹扩展方向

对钢轨裂纹进行分析时，首先需要考虑裂纹扩展的方向；陈朝阳等[11]对各剥离掉块样品纵断面上的裂纹角度进行了测量统计，在起始阶段，裂纹扩展的角度多在30°～65°之间。在本文分析中，假定第一条裂纹扩展角度与行车方向的夹角为30°，裂纹的长度为100 μm。

在讨论第2条裂纹扩展方向时，在第1条裂纹的基础上，分别沿上一段裂纹各个不同的方向建立一条10 μm的支裂纹(图2)。由于支裂纹的长度相对于主裂纹很小，可认为产生支裂纹后的裂纹尖端的应力、位移(应变)场仍等于未分支前该点处的应力、位移场[12]。因此可以通过预置支裂纹的方法来求等效应力强度因子Keff最大的方向，认为此方向即下一段裂纹的扩展方向。很多国外的学者也是用这种思想来判断复杂载荷下的裂纹扩展方向[13-17]。

计算裂纹在不同方向上、接触斑在不同位置处的应力强度因子KI和KII，依据(5)式得到不同方向上的等效应力强度因子Keff的最大值，根据等效应力强度因子Keff的最大值的大小判断出下一条裂纹的扩展方向，然后第2条裂纹在此方向上扩展100 μm。依次方法计算出整条裂纹的扩展方向。整个计算流程图如图3所示。

图2　支裂纹模型示意图Fig.2 Schematic model of branch crack

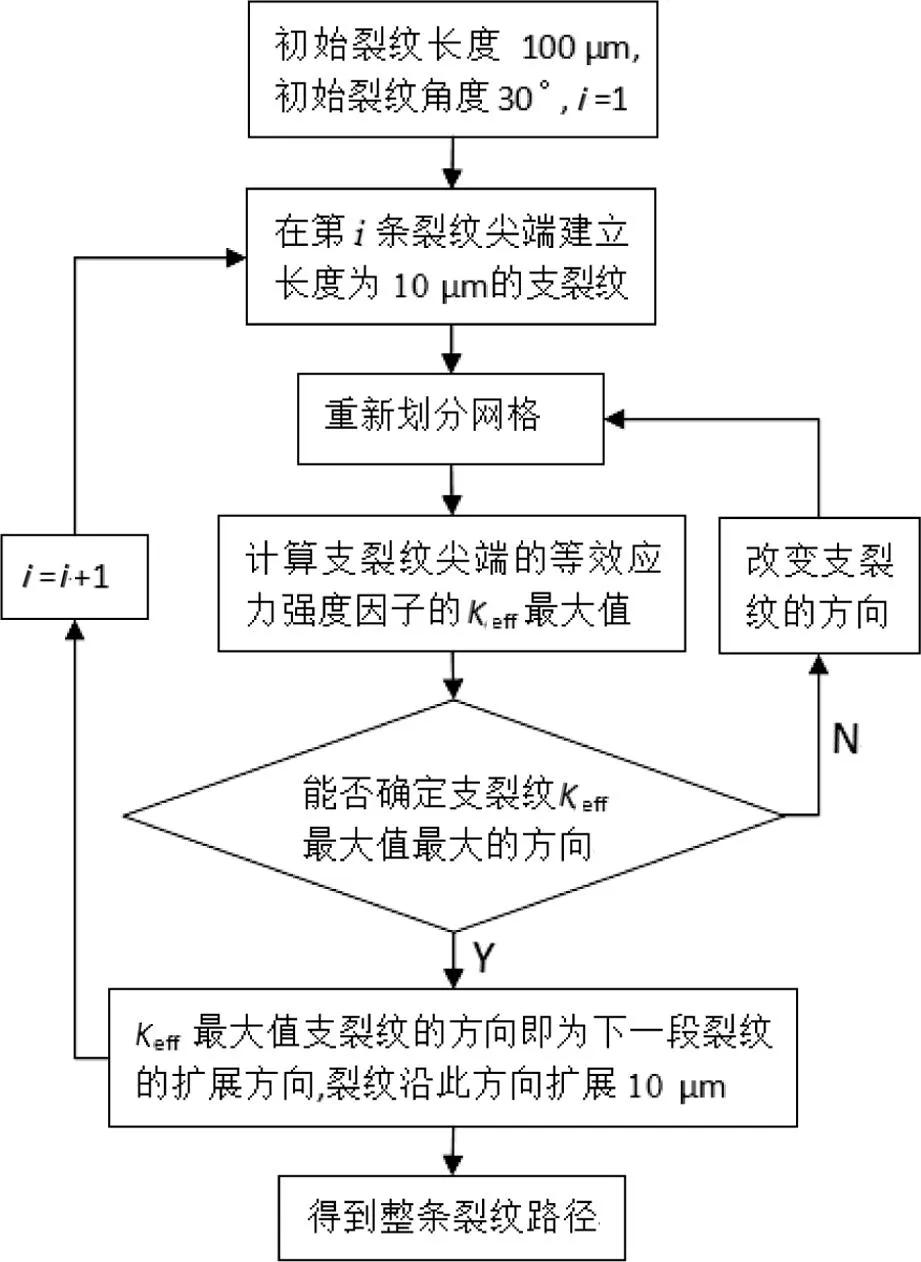
图3　整个计算过程程序流程图Fig.3 Flow chat of whole calculate process

2有限元模拟

根据我国铁路主要干线采用钢轨类型的实际状况，本次试验的钢轨类型以60 kg/m钢轨为基准；钢轨的材料为U71Mn钢[18]，U71Mn钢的力学性能如表1所示。

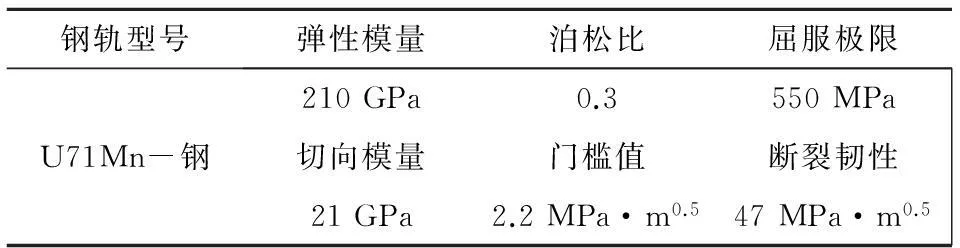
表1　U71Mn钢的力学性能

模型高为176 mm，长为600 mm，初始裂纹与行车方向的夹角为30°，长度为100 μm，在钢轨上表面中间；在不考虑轨枕影响的情况下，钢轨下端采取全约束，整体有限元模型以及裂纹尖端局部有限元模型如图4所示。载荷为车轮对钢轨的接触压力和切向力，施加在钢轨上表面，且载荷随着车轮的滚动而移动。

图4　含表面微裂纹的钢轨有限元模型Fig.4 Finite element model of rail containing surface crack

3计算结果与讨论

3.1裂纹疲劳与磨损竞争

轴重10 t的车轮纯滚动经过钢轨表面长度100 μm，角度为30°的初始裂纹的整个过程中；裂纹尖端的有效应力强度因子Keff的变化趋势如图5所示，其中x为接触斑的右边缘与裂纹之间的距离。

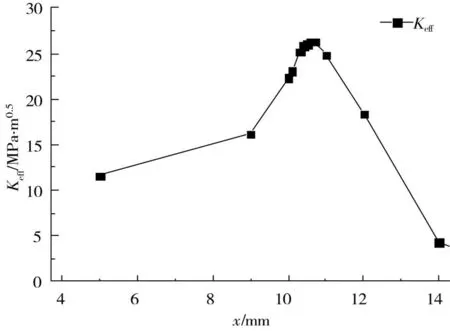
图5　裂纹扩展角度30°Fig.5 Changes of the effective stress intensity factor in the direction 30° of initial crack

由图5可知，裂纹尖端的有效应力强度因子Keff的最大值为26.3 MPa.m0.5；王文健等[19]通过疲劳试验测得的U71Mn钢的疲劳裂纹扩展参数C=4.597×10-13，m=2.88；在忽略钢轨表面磨损时，由公式(6)求得裂纹的扩展速率为：

(9)

由文献[20]可知，车轮每作用一次对钢轨表面的磨耗量为0.1 nm，由此可知，因钢轨表面材料磨损导致裂纹长度被截断的速率：

(10)

由式(9)和(10)可知，车轮每作用一次裂纹的净增长长度为：

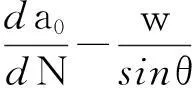
(11)

由于钢轨表面裂纹的扩展速率明显大于钢轨表面的磨损速率，因此可以判定，在10 t轴重作用下，当裂纹长度大于100 μm后，此时钢轨的破坏形式以疲劳为主。

3.2裂纹扩展方向的判断

为了进一步分析钢轨表面裂纹的扩展路径，本次分析在长100和角度30°的初始裂纹基础上，围绕着裂纹尖端每隔15°建立一条长10 μm的微小裂纹分支，如图2所示。随后，在轴重为10 t的车轮，纯滚动经过裂纹的整个过程，各个分支裂纹的裂纹尖端等效应力强度因子Keff的变化趋势如图8所示。

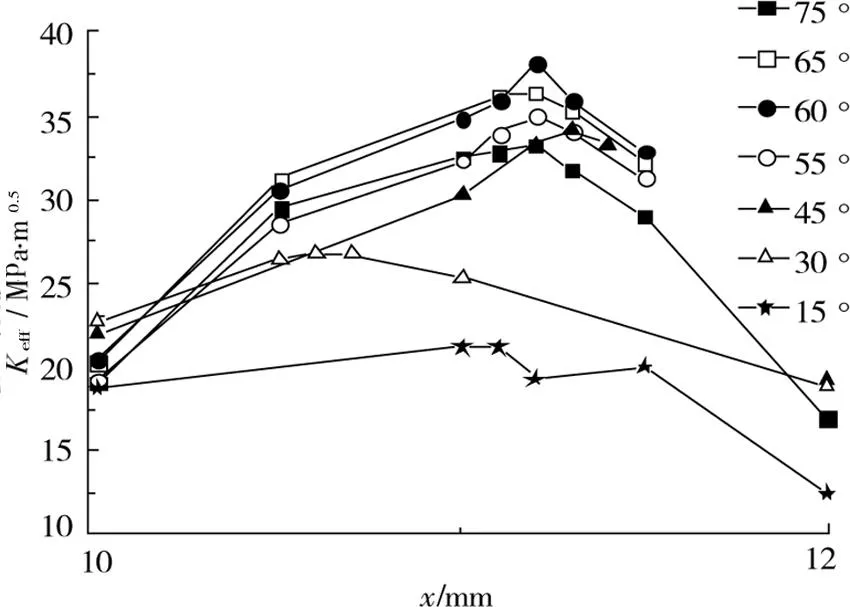
图6　不同分支裂纹等效应力强度因子KeffFig.6 Equivalent stress intensity factor Keff of different branches crack

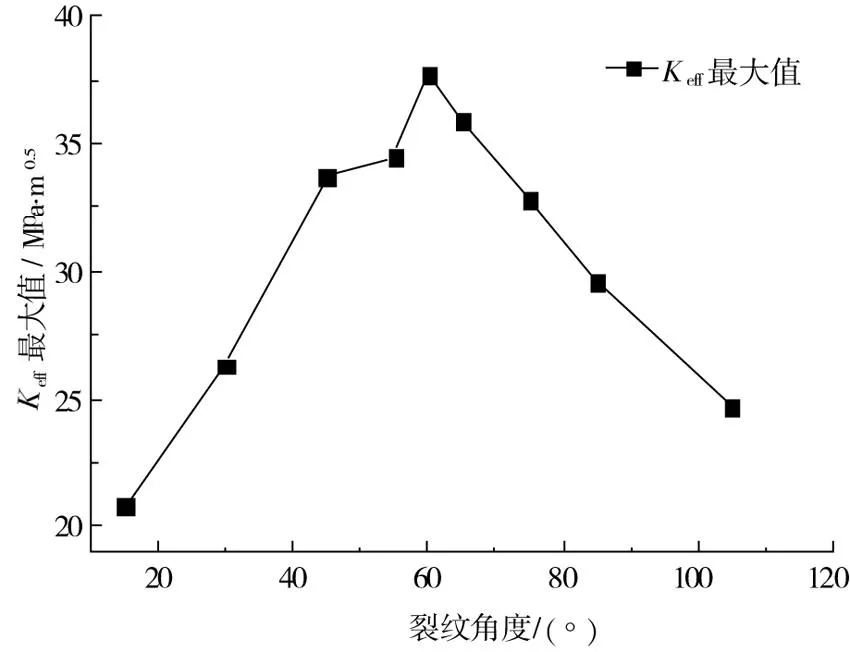
图7　不同角度分支裂纹Keff的最大值Fig.7 Maximum value Keff of different angles branches crack

从图6可以得出，当接触斑滚过裂纹表面时，最危险的位置基本上都位于接触斑边缘(10 t轴重的接触斑长度11.66 mm)。由图7可知，与钢轨表面呈60°夹角的分支裂纹的等效应力强度因子Keff的值最大，也就是说与钢轨表面呈60°夹角方向扩展速率最快，以此判定下阶段裂纹扩展方向为60°。随后在车轮循环荷载作用下，裂纹即按60°方向持续扩展100 μm后，重新以此方法对下阶段的扩展方向进行预测。不同阶段的裂纹尖端等效应力强度因子及其扩展方向如表2所示。

由表2中Keff随着裂纹长度的变化趋势可知，随着裂纹长度的增加，裂纹扩展速率先增加后减小，当裂纹长度为600 μm时，其扩展速率最快。

表2　裂纹长度、扩展角度以及Keff最大值

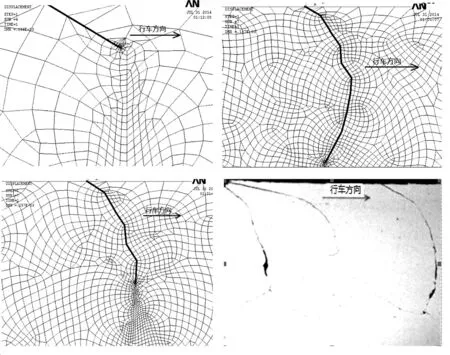
(a) 初始裂纹长度100 μm；(b) 裂纹长度600 μm；(c) 裂纹长度1 000 μm；(d) 朔黄线钢轨裂纹形貌图8　模拟路径与实验路径对比Fig.8 Comparison of crack path between simulation and experiment

由图8可知，裂纹长度在500 μm以内时，裂纹扩展方向与行车方向成锐角；当裂纹长度扩展到600 μm时，裂纹扩展角度大于90°。在裂纹长度在600到1 200 μm时，裂纹扩展角度都是大于90°，裂纹扩展方向基本稳定，出现鱼钩状裂纹的趋势。这与陈朝阳等对朔黄线剥离掉块样品纵断面上裂纹扩展路径的测量结果比较吻合，如图8(d)所示。

因此，若裂纹继续沿着与起始阶段相反的方向扩展，则会形成鱼钩状裂纹，最终形成剥离掉块。若裂纹在继续扩展过程中，再次出现转角，裂纹扩展方向一直与行车方向成锐角扩展。则裂纹损伤形式以疲劳断裂为主。

4结论

1)通过轮轨接触疲劳和磨耗的耦合分析表明，钢轨表面初始长度为100 μm的裂纹扩展速率明显大于钢轨表面的磨耗速率，也就是说，其破坏形式以接触疲劳为主。

2)随着裂纹长度增加，其扩展速率先增加后减小，当裂纹长度为600时，其扩展速率最快。

3)在裂纹初始扩展阶段，裂纹扩展方向基本与行车方向一致；当裂纹长度大于600 μm后，裂纹扩展角度超过90°，裂纹沿着与起始阶段相反的方向扩展，形成鱼钩型裂纹。

参考文献：

[1] 金学松，杜星，郭俊，等.钢轨打磨技术研究进展 [J].西南交通大学学报，2010，45(1) ：1-11.

JIN Xuesong，DU Xing，GUO Jun，et al. State of arts of research on rail grinding [J]. Journal of Southwest Jiaotong University，2010，45(1): 1-11.

[2] 金学松，刘启跃.轮轨摩擦学[M].北京：中国铁道出版社，2004.

JIN Xuesong，LIU Qiyue. Wheel-rail tribology[M]. Beijing: China Railway Press，2004 .

[3] 钟雯，董霖，王宇，等. 高速与重载铁路的疲劳磨损对比研究[J]. 摩擦学学报，2012，32(1)：96-101.

ZHONG Wen，DONG Lin，WANG Yu，et al. A comparative investigation between rolling contact fatigue and wear of high-speed and heavy-haul railway[J]. Tribology，2012，32(1)：96-101.

[4] 周剑华，任安超，吉玉，等. U71Mn钢轨踏面掉块缺陷分析[J]. 中国铁道科学，2013，34(2)：1-6.

ZHOU Jianhua，REN Anchao，JI Yu，et al. Analysis of the reasons for the spalling defects on U71Mn rail treads[J]. China Railway Science，2013，34(2)：1-6.

[5] Patel S，Gohil A V. Wheel-rail contact fatigue[J]. International Journal of Engineering Research and Applications，2013，23(2)：980-983.

[6] Palaniswany K, Knauss W G. Propagation of crack under general in-plane tension[J]. International Journal of fracture Mechanics, 1927,8(1):114-117.

[7] 郦正能，张纪奎. 工程断裂力学[M]. 北京：北京航空航天大学出版社，2012:31-33.

LI Zhengneng, ZHANG Jikui. Engineering fracture mechanics[M]. Beijing: Beijing Aeronautics and Astronautics University Press, 2012:31-33.

[8] 李庆芬. 断裂力学及其工程应用[M]. 哈尔滨：哈尔滨工程大学出版社，2007：91-94.

LI Qingfen. Fracture mechanics and engineering applications[M]. Harbin：Harbin Engineering University Press，2007：91-94.

[9] 王泽.断裂力学[M]. 哈尔滨：哈尔滨工业大学出版社，1989：34-36.

WANG Ze. Fracture mechanics[M]. Harbin：Harbin Engineering University Press，1989：34-36.

[10] Paris P C，Erdogan F. A critical analysis of crack propagation laws[J]. Journal of Basic Engineering，1963，85 (4)：528-534.

[11] 陈朝阳，张银华，刘丰庆，等. 朔黄铁路曲线下股热处理钢轨剥离损伤成因分析[J]. 中国铁道科学，2008，29(4)：28-34.

CHEN Chaoyang，ZHANG Yinhua，LIU Fengqing，et al. Analysis the damage of heat treated rail on shuohuang railway under the curve[J]. China Railway Science，2008，29(4)：28-34.

[12] Nuismer R J. An energy release rate criterion for mixed mode fracture[J]. International Journal of Fracture, 1975, 11(2):245-250.

[13] Dubourg MC, Lamacq V. A predictive rolling contact fatigue crack growth model: onset of branching, direction, and growth - role of dry and lubricated conditions on crack patterns[J]. Tribol Transact ASME, 2002,124(4)：680-688.

[14] Hourlier F, Pineau A. Propagation of fatigue cracks under polymodal loading[J]. Fatigue Eng Mater Struct, 1982,5(4):287-302.

[15] Baietto M C, Pierres E, Gravouil A, et al. Fretting fatigue crack growth simulation based on a combined experimental and XFEM strategy[J]. International Journal of Fatigue, 2013, 47(1):31-43.

[16] Trollé B, Baietto M C, Gravouil A, et al. 2D fatigue crack propagation in rails taking into account actual plastic stresses[J]. Engineering Fracture Mechanics, 2014,123(1):163-181.

[17] Brouzoulis J, Ekh M. Crack propagation in rails under rolling contact fatigue loading conditions based on material forces[J]. International Journal of Fatigue, 2012, 45(3)：98-105.

[18] 曹世豪，江晓禹，文良华. 轴重和摩擦力对轮轨接触疲劳的影响[J]. 表面技术，2013，42(6)：10-14.

CAO Shihao，JIANG Xiaoyu，WEN Lianghua. Influence of axle load and friction on the fatigue of wheel/rail contact[J]. Surface Technology，2013，42(6)：10-14.

[19] 王文健，刘启跃.PD3和U71Mn钢轨钢疲劳裂纹扩展速率研究[J].机械强度，2007, 29(6):1027-1028

WANG Wenjian, LIU Qiyue. Study on fatigue crack growth rate of PD3 and U71Mn rail steel[J]. Journal of Mechanical Strength,2007, 29(6) ：1027-1028.

[20] 罗仁，曾京，戴焕云，等. 高速列车车轮磨耗预测仿真[J]. 摩擦学学报，2009，29(6)：551-558.

LUO Ren，ZENG Jing，DAI Huanyun，et al. Simulation on wheel wear prediction of high-speed train[J]. Tribology，2009，29(6)：551-558.

(编辑蒋学东)

Research of the coupling relationship between rail crack fatigue and wear

LI Xiaotao, WEN Lianghua, LI Xu, CAO Shihao, JIANG Xiaoyu

(School of Mechanics and Engineering， Southwest Jiaotong University, Chengdu 610031, China)

Abstract：Fatigue and wear coupling model based on the finite element method software ANSYS was used to analyze the competition mechanism between fatigue and wear. The equivalent stress intensity factor Keff of the crack tip was obtained for the initial crack with 100μm and 30° under the pure rolling state and ten tons axle load, and then the equivalent stress intensity factor Keff of different length crack was obtained. The results show that, the major damage of rail is wheel/rail contact fatigue. The stress intensity factor KI increases firstly, and then decreases with the increase of crack length. In the initial extension stage of crack, the extending direction of crack is the same of the driving direction. When the crack length is more than 600 microns, the extending direction transforms into the opposite of driving direction, and forming the crack which looks like a fishhook.

Key words：ANSYS; fatigue; wear; couple; crack growth direction

中图分类号：U211.5

文献标志码：A

文章编号：1672-7029(2016)03-0441-06

通讯作者：江晓禹(1965-)，男，贵州遵义人，教授，博士，从事复合材料力学和固体接触力学方面的研究；E-mail: xiaoyujiang8@sohu.com

基金项目：国家自然科学基金重点资助项目(11472230)

收稿日期：2015-08-02