基于贝叶斯网络的渤海湾水体富营养化模型

袁德奎，姚鹏辉，徐晓甫,2，聂红涛

(1.天津大学机械工程学院，天津 300072；2.天津渤海水产研究所，天津 300457；3.天津大学环境科学与工程学院，天津 300072)



基于贝叶斯网络的渤海湾水体富营养化模型

袁德奎1，姚鹏辉1，徐晓甫1,2，聂红涛3

(1.天津大学机械工程学院，天津 300072；2.天津渤海水产研究所，天津 300457；3.天津大学环境科学与工程学院，天津 300072)

摘 要：基于渤海湾的现场监测数据，结合已有水体富营养化建模经验，用结构方程模型(SEM)对渤海湾水体富营养化因子与叶绿素a之间的因果关系进行了识别和验证.根据SEM提供的因果关系，建立了基于贝叶斯网络(BN)模型的渤海湾赤潮监控区海域水体的富营养化模型，并用监测数据对BN模型进行了检验和性能评价.研究结果表明：与物理因子相比，营养物质对渤海湾海域富营养化的影响较大；近年来无机磷一直为渤海湾浮游植物生长的限制因子，但是硅酸盐对浮游植物生长的影响程度越来越大.

关键词：富营养化模型；贝叶斯网络；结构方程模型；叶绿素a；渤海湾

随着沿海地区经济的快速发展和人口的增长，近岸海域承受着越来越重的生态环境压力.渤海湾是我国渤海三大海湾之一，位于渤海的西部，是一个典型的半封闭淤泥质浅水海湾，海水交换能力和自净能力很弱.近年来，渤海湾近岸海域一直处于严重的富营养化状态：藻类大量繁殖，溶解氧含量低，贝类种群下降，大量鱼类死亡等现象频繁发生[1].因此，建立渤海湾海域富营养化模型，分析渤海湾海域水体富营养化的成因，对科学管理该海域有重要的意义.

基于机理的确定性富营养化模型目前已有较多的成果，如营养物质平衡模型、生态-水质-水动力模型、生态结构动力学模型等.由于对海洋生态环境问题机理认识的不足，目前该类模型还较多地依赖于假设和经验关系，在应用中受到较大限制.一些基于统计方法的模型能够给出多种物理、化学、生态指标之间的关系，增进对海洋生态环境问题机理的认识，如Camdevren等[2]通过主成分分析和多元线性回归方法预测叶绿素a(chl a)与多种生物和物理、化学指标关系等的多元统计方法，但该类模型对海洋生态环境问题内在的不确定性考虑不足.基于各种不确定性理论的模型较好地考虑了海洋生态环境问题的不确定性，有很好的应用前景，如Chen等[3]提出的基于模糊逻辑理论预测藻类生物量的富营养化模型、向先全等[4]基于GA-SVM的渤海湾富营养化模型等不确定性富营养化模型等.

贝叶斯网络(Bayesian networks，BN)是在概率统计学、人工智能、信息论和图论等技术理论的基础上发展起来的一种概率图论模型，为知识表达和信息融合提供了新的技术途径.它是目前不确定知识表示和数据挖掘中最为有效的理论模型之一，已经引起国际上生态领域研究人员的广泛关注.BN模型相较于确定性模型、遗传算法、人工神经网络等方法，在海洋生态研究中的优势体现在：能更好地处理不确定性、解决模型参数时空尺度的不一致性、可以在数据量小和数据不完整的情况下获得较好的预测结果等.

然而，越来越多的研究表明，BN模型在海洋生态领域中存在模型拓扑结构建立困难和因果关系无法辨识等缺点，一旦BN模型结构建立在非真实的因果关系之上，可能导致BN模型的效果不佳、理论解释模糊和模型验证困难[5].而可以结合现有知识与统计数据，提供一个定量评估研究变量之间因果关系的结构方程模型(SEM)则可弥补BN模型的不足[6].因此，笔者首先运用SEM模型探索叶绿素a(Chl a)与富营养化因子间的因果关系，然后建立基于BN的不确定性富营养化模型，避免BN模型建立在非真实的因果关系之上，并将此方法用于渤海湾海域富营养化模型的研究中.

1　理论基础

1.1结构方程模型

结构方程模型融合了回归分析、因子分析和路径分析等统计分析方法的思想，可用来处理复杂的多变量研究数据的探究与分析.与传统统计分析方法不同，它允许自变量与因变量间存在测量误差，可以考虑变量间的直接影响、间接影响和总影响，而且可以对模型的整体进行评价.对于海洋生态环境的复杂性和高度不确定性，结构方程模型更能反映各变量之间的关系和潜在变量间的相互作用，并能模拟多因子间内在的逻辑关系.近几十年来，SEM被越来越多地用到生态问题的研究中，如富营养化、植物群落结构、生态模式和流域属性等[7-8].

结构方程模型包括潜变量和指标变量，由结构模型和测量模型组成.

(1)结构模型.表示内生潜在变量和外生潜在变量之间的关系，其模型表达式为

式中：η为内生潜在变量；ξ为外生潜在变量；B为内生潜在变量η之间的结构关系矩阵；Γ为外生潜在变量ξ对内生潜在变量η的影响矩阵；ζ为潜变量误差矩阵.

(2)测量模型.表示指标变量与潜在变量之间的关系，其模型表达式为

式中：X、Y为指标变量；XΛ为X与外生潜在变量ξ间的相关系数矩阵；YΛ为Y与内生潜在变量η间的相关系数矩阵；δ和ε分别为测量误差矩阵.

结构方程模型亦可用矩阵形式表达，即

式中：ν为包含指标变量和潜在变量的矩阵；F为回归系数矩阵；u为误差矩阵.

从广义上讲，SEM代表了一系列变量间因果假设关系到统计依赖模式的转换.通过把因果假设关系转化为可验证的数学模型，SEM提供了一个对理论模型的可信度进行量化和检测的途径.从技术层面上来说，SEM会依据输入的相关矩阵Σ和假设模型，用一定的数学方法找出另一个相关矩阵，称为再生矩阵(Σ(θ))，Σ(θ)既符合原先的假设模型，又与Σ在某种意义上最接近，由Σ与Σ(θ)间差距的大小来判断模型与数据之间的吻合程度.

1.2贝叶斯网络

贝叶斯网络(BN)又称贝叶斯信度网络(BBN)，是一种基于概率知识的图解模型，它可以有效地表示变量之间的相互不确定性关系.一个贝叶斯网络主要由两部分组成，一部分是有向无环图(DAG)，另一部分是条件概率表(CPT).网络中，有向无环图由节点集和有向边集合组成，每个节点代表随机变量，节点间的有向边(由父节点指向其后代子节点)代表了节点间的依赖关系；每个节点都对应一个条件概率表，表示该变量与父节点之间的关系强度，没有父节点的用先验概率进行信息表达.

用贝叶斯网络解决实际问题需要先分两步建立贝叶斯网络模型.首先要建立贝叶斯网络的有向无环图，即分析确定系统中主要变量并建立变量之间的因果关系，这是一个定性的过程，称为贝叶斯网络结构学习.当贝叶斯网络结构建立后，需要知道变量之间的定量关系即确定出条件概率表，这一过程称为贝叶斯网络的参数学习，目前常用的方法是从数据样本中学习节点的概率分布，这种数据驱动的学习方法具有很强的适应性.根据观测状况可将数据样本分为完备数据集和不完备数据集.对完备数据集常用的学习方法有最大似然估计法和贝叶斯方法；对不完备数据集的学习一般要借助于近似的方法，如Monte-Carlo方法、Caussian逼近和EM算法等.

用建立好的贝叶斯网络解决实际问题的过程就是贝叶斯网络概率推理的过程.概率推理就是在贝叶斯网络模型确定的情况下，根据已知证据节点变量的概率分布，利用条件概率的计算方法，计算出所感兴趣的查询节点变量发生的概率.

2　研究区域与数据来源

本文研究区域为渤海湾海河入海口南部近岸的赤潮监控区(见图1)，模型的建立及验证均采用该监控区域的实测数据.监控区的地理位置为N38°49′20″～N38°55′00″，E117°37′00″～E117°50′00″，内设6个站位，监测时间为2006年和2007年夏季的6—8月，监测频率为每两周6次，监测指标包括：表层水温(T)、pH值、盐度(S)、化学耗氧量(COD)、溶解氧(DO)、透明度(SD)、溶解性无机氮(DIN)、磷酸盐(PO4)、硅酸盐(Si)以及叶绿素a(Chl a)等等.初始样本数据共93个，随机选择其中的73个样本为模型建立的训练数据，剩余的20个样本则作为模型的验证数据.

图1　研究区域及观测站位分布Fig.1 Location of Bohai Bay and the six sample stations

3　基于SEM的环境变量间因果关系探索

3.1SEM的建立

由于导致渤海湾海域水体污染的原因比较复杂，根据水体富营养化的形成机理、已有的研究成果和建模经验[9]，建立结构模型(见图2)来研究渤海湾海域营养物质(nutrients)和物理因子(physical factor)两个环境潜变量对浮游植物(phytoplankton)的影响.

图2　结构模型Fig.2 Structural model

营养物质和物理因子对浮游植物的生长影响较大，而在海洋中海水的表层水温(T)、盐度(S)及pH值对浮游植物的生长具有比其他物理因子更为显著的影响效果[10-12]；海洋中的营养盐N和P通常制约浮游植物的生长与繁殖；而在海洋带上升流地区Si是控制浮游植物生长的重要元素[13-14].因此，在本研究中用DIN、P、Si分别作为营养物质的3个指标变量，T、pH、S分别作为物理因子的3个指标变量，即形成营养物质和物理因子的测量模型.另外，由于叶绿素a(Chl a)浓度一般是浮游植物生物量最直接的代表，在本研究中，用叶绿素a浓度作为浮游植物的指标变量形成相应的测量模型.最终，结构模型与各自的测量模型相结合，集成为完整的SEM(如图3所示).图3中：1λ～7λ为观察变量和潜变量的关联系数；1γ～3γ为外源潜变量与内生潜变量间的关联系数；1δ～6δ为外源潜变量的观察变量的测量误差；1ε为内生潜变量的观察变量的测量误差；1ψ为结构误差.

图3　完整的SEMFig.3 Complete SEM

3.2模型因果关系的检验

采用amos21软件绘制已建立的富营养化模型，其中假设叶绿素a是浮游植物的完美测量(没有测量误差，λ7=1，ε1=0).通过amos21软件对数据进行拟合及标准化处理，本研究用的拟合函数为适合小数据集的贝氏估计法，在贝氏估计法中主要使用后预测p值来评估模型的整体效果，后预测p值代表未来数据的卡方值大于或等于观察数据卡方值的概率，通常情况下，当后预测p值小于0.05或大于0.95时，表示该模型与数据不适配.模型经过反复修正和计算，最终得到SEM模型的后预测p值为0.18，在合理的范围之内.

由图4 SEM的标准化路径系数计算结果可以看出，在潜变量中营养物质对叶绿素a的浓度有最大的影响(γ1=- 0.33)，物理因子次之(γ2=- 0.23).在所有指标变量中，硅酸盐对叶绿素a浓度的影响最大(0.75×0.33＝0.246).

图4　SEM标准化路径输出结果Fig.4 Standardized path output of SEM

4　基于BN的富营养化模型

4.1贝叶斯网络结构的确定

当SEM模型与实测数据拟合良好时，表明其测量模型和结构模型都是合理的，即该SEM模型的观测变量能够很好地测量潜变量，潜变量之间的因果关系也是可信的.因此，根据第3节中SEM模型的拟合分析结果，建立完整的BN模型拓扑网络结构，BN模型潜变量的父节点可参考对应SEM模型的测量模型部分，而潜变量之间的因果关系可与对应SEM模型中的结构模型相同.由此，得到完整的富营养化BN模型，如图5所示.

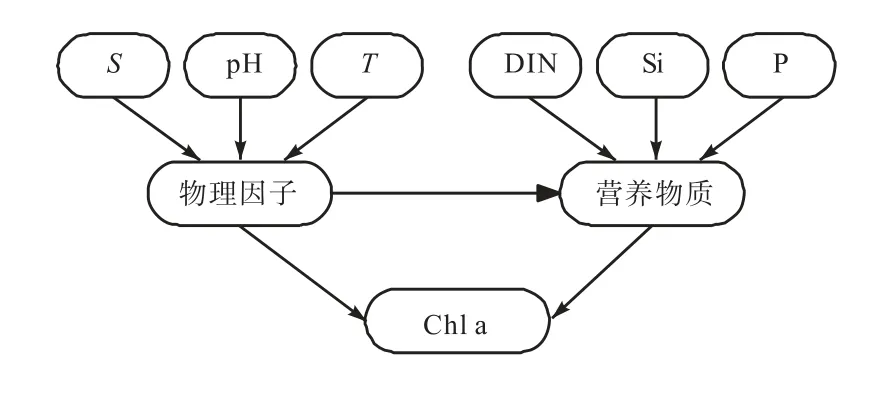
图5　富营养化BN模型Fig.5 BN model of eutrophication

本文采用Netica分析软件建立上述贝叶斯网络模型并进行分析.鉴于模型建立既要满足准确度又要满足精确度的要求，对于节点区间的划分，一般将节点区间的数量定义为4个或更少.因此，本文对影响叶绿素a浓度的预测变量的节点区间定义为4个；为了清晰表征叶绿素a浓度上升、下降及基本稳定3种变化趋势，将其节点区间定义为3个.考虑到变量先验概率的一致性，将每个节点区间内定义相近数量的实测数据，以此确定节点区间的边界值.由于模型中含有潜在变量，选用能够解决缺失数据集问题的EM学习算法来自动计算CPT的值，BN模型学习结果见图6.

图6　BN学习结果Fig.6 Learning outcomes of BN

4.2 模型效果检验

对BN模型的评价主要是依据其对现有数据的模拟效果和对现实规律的反映情况进行.因此，本文采用准确度分析和敏感性分析来评估富营养化BN模型的性能.

4.2.1准确度分析

BN模型的准确度分析最常见的方法是误差矩阵，利用误差矩阵对模型中目标变量预测值和样本真实值进行比较，可以清晰地展现BN模型预测错误的样本个数.本文用训练数据之外的20个实测数据作为样本对BN模型进行准确度分析，来评估BN模型的性能(见表1).经过计算，20个样本中，BN准确预测了16个样本，正确率为80%，而预测错误的样本也与其实际值所属区间相邻.

表1　BN模型的错误矩阵Tab.1 Error matrix of BN model

4.2.2敏感性分析

BN模型的敏感性分析主要用来评估某个节点受其他节点的影响程度，用方差减少量(variance reduction，VR)来衡量，通过敏感性分析，可以评估BN模型是否符合建模预期.本文主要通过评估各变量对叶绿素a浓度的影响来检验BN模型的行为是否符合实际情况，VR用Marcot等[15]推荐的方法计算.选择叶绿素a节点，对其做敏感性分析，来判定叶绿素a受其他节点的影响程度，利用敏感性分析获得的结果来判定目标节点是如何被其他节点影响的.BN模型的敏感性分析表明：叶绿素a对营养物质变化的响应更为敏感(VR＝6.16)，远远大于物理因子的响应(VR＝0.927,7)；在6个变量中Si对叶绿素a浓度的影响较大(VR＝0.312,3)，而物理因子中pH值对叶绿素a浓度的影响较大.

由此可以看出，BN模型的敏感性分析与SEM模型的结论是一致的，表明BN模型变量间的因果关系建立在真实可信的基础上，能够较好地揭示因子之间隐含的因果关系.

4.3相关性分析

应用简单的Pearson相关对该赤潮监控区数据进行相关性分析(见表2).由表2可以看出硅酸盐与叶绿素a浓度的相关性大于其他变量的相关性，这也表明模型从数据层次上与实际相符合.

表2　Chl a与预测变量间的相关性分析结果Tab.2 Correlation analysis result of Chl,a and predictor variables

4.4结果分析

基于BN模型的敏感性分析，营养物质对叶绿素a浓度的影响大于物理因子.这与常识认知是一致的，对于该海域赤潮的控制来说，应该尽量减少该海域营养物质的入海量.

营养物质对叶绿素a浓度的影响程度由高到低依次为硅酸盐、磷酸盐和DIN，而现有研究结果表明，渤海湾海域营养盐结构主要为磷限制.产生这种现象的原因可能有：首先在对渤海湾海域浮游植物进行研究时发现，不同观测时期硅藻均是该海域浮游植物的优势种[16]，而Si对硅藻的生长和繁殖有着重要的作用，因此，Si可能直接影响该海域浮游植物生物量；其次，对于硅藻其在海洋中对Si和N的吸收比为1∶1[17]，当海水中Si/N的值小于1时，该海域可能存在潜在的硅限制，而渤海湾海域中Si/N的值为0.67，因此Si对浮游植物生物量的影响可能大于DIN的影响.

在物理因子中pH值对叶绿素a浓度的影响最大，结果与尹翠玲等[18]研究结果相符，这种现象主要由于渤海湾海域夏季硅藻是浮游植物的优势种，而硅藻与pH值间的相关性均大于T和S.

5　结 论

本文基于现场监测数据，用贝叶斯网络建立了渤海湾海域叶绿素a浓度与相关环境因子的定量关系模型，并用结构方程模型做了进一步验证，得出如下结论.

(1)基于BN模型的敏感性分析和SEM模型分析可以看出营养物质对叶绿素a浓度的影响大于物理因子.对于该海域赤潮的控制来说，应该尽量减少该海域的营养物质入海量.

(2)模型结果显示，在目前的富营养化状态下，相比于磷，硅可能是渤海湾海域更为关键的限制性营养物质；而在物理因子中pH值对叶绿素a浓度的影响较大.

参考文献：

［1］Wang Xiulin，Cui Zhengguo，Guo Quan，et al.Distribution of nutrients and eutrophication assessment in the Bohai Sea of China[J].Chinese Journal of Oceanology and Limnology，2009，27(1)：177-183.

［2］Camdevren H，Demyr H，Kanik A，et al.Use of principal component scores in multiple linear regression models for prediction of Chlorophyll-a in reservoirs[J].Ecological Modelling，2005，181(4)：581-589.

［3］Chen Qiuwen，Mynett A E.Modelling algal blooms in the Dutch coastal waters by integrated numerical and fuzzy cellular automata approaches[J].Ecological Modelling，2006，199(1)：73-81.

［4］向先全，陶建华.基于GA-SVM的渤海湾富营养化模型[J].天津大学学报，2011，44(3)：215-220.Xiang Xianquan，Tao Jianhua.Eutrophication model of Bohai Bay based on GA-SVM[J].Journal of Tianjin University，2011，44(3)：215-220(in Chinese).

［5］Alameddine I，Cha Y，Reckhow K H.An evaluation of automated structure learning with Bayesian networks：An application to estuarine chlorophyll dynamics[J].Environmental Modelling &Software，2011，26(2)：163-172.

［6］Druzdzel M J，Simon H A.Causality in Bayesian belief network[C]//Proceedings of the 9th Annual Conference on Uncertainty in Artificial Intelligence.Washington：Morgan Kaufmann Publishers Inc，1993：3-11.

［7］Arhonditsis G，Pael H，Valdesweaver L，et al.Application of Bayesian structural equation modeling for examining phytoplankto dynamics in the Neuse River Estuary(North Carolina，USA)[J].Estuarine，Coastal and Shelf Science，2007，72(1/2)：63-80.

［8］Chen Y H，Lin L S.Structural equation-based latent growth curve modeling of watershed attribute-regulated stream sensitivity to reduced acidic deposition[J].Ecological Modelling，2010，221(17)：2086-2094.

［9］颜小品，李玉照，刘 永，等.基于结构方程模型的滇池叶绿素a与关键影响因子关系识别[J].北京大学学报：自然科学版，2013，49(6)：1031-1039.Yan Xiaopin，Li Yuzhao，Liu Yong，et al.Identifying the influence of water chemistry on chlorophyll a in Lake Dianchi：A structural equation modeling analysis[J].Acta Scientiarum Naturalium Universitatis Pekinensis，2013，49(6)：1031-1039(in Chinese).

［10］Hinga K R.Effects of pH on coastal marine phytoplankton[J].Marine Ecology Progress Series，2002，238(28)：281-300.

［11］Flöder S，Jaschinski S，Wells G，et al.Dominance and compensatory growth in phytoplankton communities under salinity stress[J].Journal of Experimental Marine Biology and Ecology，2010，395(1/2)：223-231.

［12］Lopes J F，Cardoso A C，Moita M T，et al.Modelling the temperature and the phytoplankton distributions at the Aveiro near coastal zone，Portugal[J].Ecological Modelling，2009，220(7)：940-961.

［13］Vitousek P M，Howarth R W.Nitrogen limitation on land and in the sea：How can it occur[J].Biogeochemistry，1991，13(2)：87-115.

［14］Hecky R，Kilham P.Nutrient limitation of phytoplankton in freshwater and marine environments：A review of recent evidence on the effects of enrichment[J].Limnology and Oceanography，1988，33(4)：796-822.

［15］Marcot B G，Steventon J D，Sutherland G D，et al.Guidelines for developing and updating Bayesian belief networks applied to ecological modeling and conservation[J].Canadian Journal of Forest Research，2006，36(12)：3063-3074.

［16］Wei H，Sun J，Moll A，et al.Phytoplankton dynamics in the Bohai Sea—Observations and modelling[J].Journal of Marine Systems，2004，44(3/4)：233-251.

［17］Brzezinski M A.The Si：C：N ratio of marine diatoms：Interspecific variability and the effect of some environmental variables[J].Journal of Phycology，1985，21(3)：347-357.

［18］尹翠玲，张秋丰，崔 健.2008—2012年渤海湾天津近岸海域夏季浮游植物组成[J].海洋科学进展，2003，31(4)：527-537.

Yin Cuiling，Zhang Qiufeng，Cui Jian.Phytoplankton composition in Bohai Bay Tianjin coastal area in summer from 2008 to 2012[J].Advances in Marine Science，2003，31(4)：527-537(in Chinese).

(责任编辑：田 军)

Water Eutrophication Model of Bohai Bay Based on Bayesian Networks

Yuan Dekui1，Yao Penghui1，Xu Xiaofu1,2，Nie Hongtao3
(1.School of Mechanical Engineering，Tianjin University，Tianjin 300072，China；2.Tianjin Bohai Sea Fisheries Research Institute，Tianjin 300457，China；3.School of Environmental Science and Engineering，Tianjin University，Tianjin 300072，China)

Abstract：Based on the monitoring data and existing modeling experience in water eutrophication model，a structural equation model(SEM)was developed to understand the causality between eutrophication factors and chlorophyll a.According to the causal relationship between the variables provided by SEM，a water eutrophication model was built for the red tide-monitoring area in Bohai Bay based on Bayesian networks(BN)，and BN model performance was tested and assessed using the monitoring data.The results demonstrate that in Bohai Bay nutrients have greater influence on the eutrophication than physical factors.In recent years，inorganic phosphorus has become the restriction factor influencing the growth of phytoplankton in Bohai Bay.However，the effect of silicate on phytoplankton growth is becoming more and more significant.

Keywords：eutrophication model；Bayesian networks(BN)；structural equation modeling；chlorophyll a；Bohai Bay

通讯作者：徐晓甫，xuxiaofu@tju.edu.cn.

作者简介：袁德奎（1972—），男，博士，研究员，dkyuan@tju.edu.cn.

基金项目：教育部新世纪优秀人才支持计划资助项目(NCET-12-0406)；天津市水产局青年科技资助项目(J2014-05).

收稿日期：2014-07-31；修回日期：2014-11-05.

DOI:10.11784/tdxbz201407093

中图分类号：X171；TP181

文献标志码：A

文章编号：0493-2137(2016)03-0320-06

网络出版时间：2014-11-24.网络出版地址：http://www.cnki.net/kcms/doi/10.11784/tdxbz201407093.html.