径向流空气纯化器内流场的模拟与分析
唐忠利,徐明杨,张 俊
(1.天津大学化工学院,天津 300072;2.化学工程联合国家重点实验室(天津大学),天津 300072)
径向流空气纯化器内流场的模拟与分析
唐忠利1,2,徐明杨1,2,张 俊1,2
(1.天津大学化工学院,天津 300072;2.化学工程联合国家重点实验室(天津大学),天津 300072)
摘 要:运用计算流体力学(CFD)的方法研究了8万吨空气纯化器内部流场分布及影响因素.研究发现,吸附和脱附过程中,内外流道横截比达到一定值时可以使气流均匀度达到最大值,降低分子筛床层的空隙率两床层气流均匀度都有所提高.此外,加入导气锥会使吸附过程床层气流均匀度下降较小,但是可以使脱附过程中床层内流场均匀度有较大上升.最终提出最优的提高气流均匀度的方案:同时降低分子筛和氧化铝床层空隙率到0.33和0.35;加入锥体,使脱附和吸附过程床层压降小幅增加,两床层内得到更均匀的气流分布.
关键词:空气分离;径向流;流体分布;结构优化;CFD模拟
空气纯化器是在空气分离过程中用来除去高压空气中的水分、二氧化碳、烃类等杂质,避免在后续流程中发生冰堵和爆炸等危害的关键装置[1].工业上常用的纯化器有立式轴向流纯化器、卧式纯化器、立式径向流纯化器3种.立式径向流纯化器相对前两者有流通界面大、床层压降小、空间利用率高等优点,因此,也更能适应空分设备规模增大的要求.
径向流有4种流动形式,分别为向心z型流、离心z型流、向心π型流和离心π型流.径向流装置最开始用作一些石油化工反应的反应器,之后空分领域开始用大型的径向流装置来纯化空气.径向流装置的操作效率很大程度上取决于气流沿装置的轴向分布,它影响着反应的转化率和选择性、反应器中温度的分布,甚至影响反应器的正常操作[2-3],在大型的空分纯化器中则直接影响空气的纯化效果.因此,研究者对径向流装置轴向气流均匀度的影响因素做了很多研究.
宋续祺等[ 4 ]等通过理论和实验探究了直径500,mm的冷模反应器的主流道轴向的压力场与速度场分布,得出在4种流动方向中,离心π型流的床层流场分布最均匀;并且根据其实验模型提出动量交换系数的关联式,能够很好地预测主流道的压力分布.Heggs等[5]通过数值模拟的方法建立特定模型预测4种流动方向的移动床径向流反应器中的流场分布,得出向心π 型流的床层流场分布最均匀.Heggs 等[6]还拓展其模型预测多床层的径向流空气吸附器中流场分布与压力曲线,模型预测与其实验结果吻合很好.Kareeri等[7]运用计算流体力学方法研究了4种流型的径向流反应器中流场分布,其结果与实验数据吻合,并以宋续祺等的径向反应器为依据简化出物理模型,阐述了中心流道和流道截面积比,床层空隙率、开孔板的开孔率等因素对床层气体分布的影响.Mu等[8]在实验结果的基础上建立了一个完整的二维流体力学模型研究向心π型流反应器中流场,并提出基于穿孔速度的床层中流场均匀度评价标准.最后提出径向流反应器的两步优化设计方案:首先确定最佳中心流道与环流道截面积比,之后通过减小末端开孔率来减小末端流量,消除末端效应.Manjhi等[9]采用格子Boltzmann方法对含有床层的吸附器内三维速度场和浓度分布曲线进行了数值求解,重点分析了多孔介质中空隙率对浓度分布以及流体均布的影响,特别是近壁面处流体的流动特性,模型计算采用柱坐标,数值计算结果与测绘数据相吻合.李瑞江等[10]测定了大型径向反应器中流道静压变化和穿孔阻力,通过数学拟合获得动量交换系数和测流穿孔阻力系数,发现穿孔阻力系数与小型试验相比有所提高.Li 等[11]又测量了小型多层π 型流反应器流道与床层内的压力分布和速度场.
从以上文献可知,径向流中流体的流向、流道的截面积比值和床层孔隙率都会影响流体轴向的均匀度,而且研究者根据不同的物理模型总结了一定规律.但以上研究多为实验室小型试验或石化领域的单床层小型反应器.然而,随着空分装置的大型化,径向流空分纯化器的规模不断增大,流速成倍增加,流动的湍流特性增强,其轴向不均匀性也更加凸显,且空气纯化器为多床层,每一层的吸附情况对下一层的吸附效率都有很大影响,流体轴向均匀性要分层研究.为此,笔者以某工厂8万吨径向空气纯化器为原型,通过CFD数值模拟的方法研究纯化器中流体在床层中的轴向均匀度和纯化器的结构因素对流体均布的影响.
1 径向流纯化器的流动特点
在纯化器纯化气体的过程中,压缩空气先从纯化器底部进入环形流道,之后穿过氧化铝和分子筛吸附层,除掉空气中的水蒸气和二氧化碳、烃类等杂质,最后经除尘进入中心流道,流出纯化器.而在再生过程中,氮气的流动方向正好相反,氮气从上端入口进入中心流道穿过床层流入环流道后流出纯化器,如图1所示.气体在两个流道流动的过程中质量是不断变化的,质量不断减少的流道叫做分流道,质量不断增加的流道叫做集流道.变质量流动时,分流道和集流道中压力也不断变化,主要有两点原因:一是流动过程中气体与粗糙壁面和多孔板间的摩擦作用使气体沿流动方向静压力降低;二是气体的速度大小变化引起的动压力与静压力的转变.由于主要吸附质水、二氧化碳和烃类在空气中的密度都很小,所以纯化器工作中可以认为气量是一定的.在吸附过程中,同样还涉及到吸热放热问题,但由于吸附的气量很小,这部分热量可忽略不计.
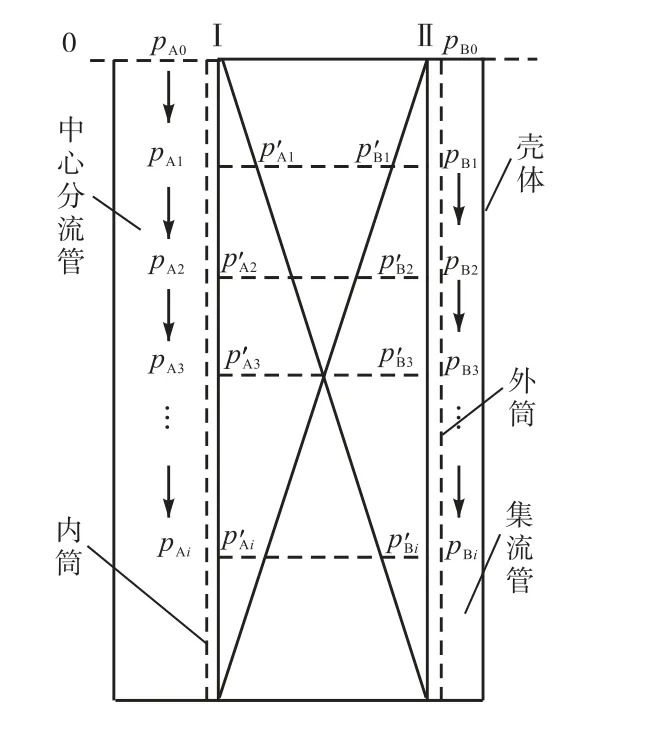
图1 径向流纯化器流体均匀分布示意Fig.1 Schematic diagram of flow uniform distribution in radial flow adsorber
图1为径向流纯化器流体均匀分布示意.图中:pAi为流道中压力;pBi为集流道中压力;pA′i为床层在分流道一侧的压力;p′Bi为床层在集流道一侧的压力.由于床层各高度处气体流量Q正比于,所以要想使床层内流体达到均匀分布的效果,必须满足不同高度的床层两侧压差相等,即

则床层流场分布均匀度可表示为

其中

式中ΔAi和ΔBi为相应一侧的穿孔阻力,代入式(1)得

如果穿过多孔板的压降ΔAi和ΔBi与床层压降相比,足够小,可忽略,则床层内气流均布条件可以表示为

流场分布均匀度可以表示为


图2 空气纯化器的物理模型Fig.2 Physical model of air adsorber
即床层两侧压差可以用同一高度上两流道内静压力差代替.
2 径向流纯化器吸附与脱附过程中流体分布的CFD模拟
2.1物理模型
纯化器结构复杂,在不影响计算精度和研究目的的前提下,这里先对实体物理模型进行如下简化:
(1)不考虑出入口复杂结构的影响;
(2)不考虑制造因素并忽略除尘区;
(3)中心管和环形管都简化为多边界.
将实体结构转换为二维轴对称平面模型,如图2所示,这样将大大减少计算量,其中床层两侧虚线是开孔板,上部实线是不开孔的部分,较薄的床层为氧化铝床层,较厚的为分子筛床层.
空气纯化器的原始尺寸见表1,吸附过程气流方向如图2所示,脱附过程气流方向与图1正好相反.

表1 空气纯化器的原始尺寸Tab.1 Original size of air adsorber mm
2.2数学模型
模拟过程中气体是单相、不可压缩、稳态、绝热的,吸附过程中反应器温度保持在282,K,脱附过程中反应器温度保持在298,K.所以,纯化器中气流的控制方程有连续性方程和动量守恒方程.
连续性方程

动量方程


本文湍流模型选择标准k-ε方程,其中湍动能k和速度值耗散ε由式(9)和式(10)得出,即

式中:Gk为由平均速度值梯度引起的湍动能k的产生项;Gb是由浮力引起的湍动能k的产生项;YM代表可压缩湍流波动耗散对全耗散率的贡献;C1ε、C2ε和C3ε均为常数;σk和σε分别是湍动能k和耗散率ε中的湍流普朗特数;Sk和Sε均为自定义的源项.
湍流黏性tμ的计算式为

模型常数C1ε、C2ε、Cμ、σk和σε的默认值分别是:C1ε=1.44,C2ε=1.92,Cμ=0.09,σk=1.0和σε=1.3.
在流道中,动量方程右侧无源项.而吸附床层和多孔板结构复杂,不易直接采用真实结构,在此引入多孔介质模型和多孔跳跃模型[12]分别进行简化.通过对空隙率、颗粒当量直径、阻力项的计算来体现床层和多孔板.多孔介质中的动量方程具有附加的动量源项,它由两部分组成,一部分是黏性损失项(式(9)右侧第1项),另一部分是惯性损失项(式(9)右侧第2项),即

式中:Si为i方向的动量源项;|v|为速度值的大小;Cij、Dij为规定矩阵C、D中的元素.在多孔介质单元中,动量损失对压力梯度有贡献,压降正比于流速.对于各项同性的多孔介质,式(12)可以简化为

用两个对角矩阵分别简化方阵D和C,1/α和C2分别作为对角上的元素.α表示渗透性,C2表示惯性阻力因子.二者都可以通过欧拉公式[13]计算得出,欧拉公式是个半经验公式,具体形式如下:

式中:ϕ为床层空隙率;Dp为颗粒直径.
多孔跳跃模型是多孔介质模型的一维简化形式.由于穿孔速度值比较大,孔板较薄,惯性阻力项起主导作用,可以忽略黏性阻力项,在多孔板处动量源项可以表示为

式中i表示与多孔板相垂直的轴,本文中表示y轴.根据经验公式可以表示为

式中:fA为开孔面积;AP为开孔板的总面积;C为系数,它与雷诺数Re以及板厚与开孔径的比t/D有关,当t/D>1.6并且Re>4,000时,C≈0.98,本文中C 取,0.98.
2.3求解方法及边界条件
吸附过程和脱附过程均选择Fluent 6.3 2D求解器,求解器设置为压力基隐式求解.
吸附及脱附过程模拟的边界条件如表2所示.入口速度设为常数,吸附为4.32,m/s,脱附为6.07,m/s;出口为自由出流;壁面无滑移;对称轴上所有变量的径向梯度为零.

表2 吸附及脱附过程模拟的边界条件Tab.2 Boundary condition of adsorption and desorption processes simulation
2.4网格划分
尺寸小的网格能保证较高的计算精度,但是采用过小的网格需要占用更大的计算资源和内存,而用尺寸很大的网格又容易引起结果失真.为了优化利用计算资源并达到很好的计算精度,本文研究的模型中5个区域均采用四边形结构化网格,最开始选用15,mm网格进行计算,然后缩小网格大小至10,mm,发现精度并没有提高,所得床层整体均匀度结果几乎相同,均匀度值约为0.875.所以在以后的模拟中网格大小均采用15,mm,此时网格数量约为169,000.
3 结果分析与讨论
3.1吸附和脱附过程中床层气流分布不均匀性
图3中6条曲线分别是吸附和脱附过程中中心管道、两床层之间和环形管道的静压力曲线.由于氧化铝床层比较薄,两层之间的静压力和环形管道的静压力很接近,在图中压差变化不明显.这里先以两床层为一整体讨论它们整体压差变化.在吸附过程中,环形流道是分流道,中心流道是集流道.环形流道中,沿流动方向,摩擦阻力使得静压力下降而速度变慢引起的动量因素使得静压力升高,两者作用相反,而摩擦力起到主导作用,所以流道内静压力有约为400,Pa的下降;在中心流道中,沿流动方向摩擦阻力和动量因素都使静压力降低,两者的协同作用使得中心流道内压力降低约为1,400,Pa.两流道内压降的差异导致纯化器上部床层两侧压力差明显比下部大,床层整体均匀性较差.根据第1节所述,可以通过增大中心流道直径而减小环流道宽度来使两流道压降趋同来提高吸附过程的床层气流均匀度.

图3 吸附和脱附过程中内外流道及两流道之间的静压力轴向分布Fig.3 Axial static pressure distribution of the inside,outside and middle flow channels during adsorption and desorption processes
在脱附过程中,中心流道内摩擦阻力与动量因素作用相反,摩擦阻力起主导作用,使中心流道内静压力沿流动方向有约50,Pa的下降.环流道内,摩擦阻力和动量因素均使得静压力下降,使得沿流动方向有约150,Pa的压力降.两流道内压降的差异造成床层内气流的轴向不均匀.根据第1节所述,可以通过增大中心流道直径、减小环流道宽度的方法来提高气流均匀度.
3.2中心流道与环流道横截比对气流均匀度的影响
由图4中可见在吸附过程中分子筛和氧化铝床层轴向气流均匀度随着中心流道和环流道的横截比呈先上升后下降的趋势,但两者的变化趋势并不完全相同.氧化铝床层最大均匀度约为0.937,出现在内外流道横截比约为0.84的位置.而分子筛床层的最大均匀度约为0.919,出现在内外流道横截比约为0.98的位置.在本文所取的点中,中心流道半径为1,000,mm、内外流道横截比为0.887时得到的两流场的均匀度几乎都处于最理想的状态.因此相对于原来的纯化器尺寸,适当增大内流道的半径,减小环形流道的宽度,能够起到增加两床层轴向气流均匀度的作用.

图4 吸附过程中两床层中流场均匀度随内外流道横截比的变化Fig.4 Changes of flow uniformity in two beds along with the cross-sectional area ratio of the inside to outside flow channels during adsorption process
图5为最佳横截比时两流道及床层间的静压力,与图4对比可得出:当内外流道横截比增大时,由于中心流道直径变大,气流速度变慢,与壁面之间的摩擦力变小引起的压力降减小,且沿着气流方向的速度变化也因整体速度变慢的原因而缩小,使得动量因素带来的压降也减小,共同使得中心管内压降由原来图3中的约1,400,Pa变为图5中的1,100,Pa左右.而环形管道变窄,气流速度增加,与壁面的摩擦力增大,由于摩擦力起到主导作用,因而环形流道内压降有所上升,由原来图3中的约400,Pa变为现在图5中的600,Pa左右,因而两流道内气流方向压降更加接近,整体均匀度提高.

图5 吸附过程中n=0.887时内外流道及两流道之间的静压力轴向分布Fig.5 Axial static pressure distribution of the inside,outside and middle flow channels during adsorption process when n=0.887
当内外流道横截比继续增大,直到1.209时,床层均匀性就会相对变差.这是因为当继续增大中心流道直径、缩小环流道宽度时,中心流道内压降继续变小,而环流道压降继续增大,导致环流道内压降大于中心流道内压降,使得床层下部压差大于上部压差,床层内气流反而向不均匀趋势发展.
在脱附过程中,两床层的流场均匀度随内外流道横截比的变化有类似的规律(见图6),不过最优的位置出现得比较靠前,之后均匀度随着内外流道横截比增大而减小.分子筛床层最大轴向均匀度约为0.991,出现在内外流道横截比约为0.47处,氧化铝床层最大均匀度约为0.986,出现在内外流道横截比约0.38处.可见减小最初内外流道横截比能够增大脱附过程中两床层的气体分布均匀度.
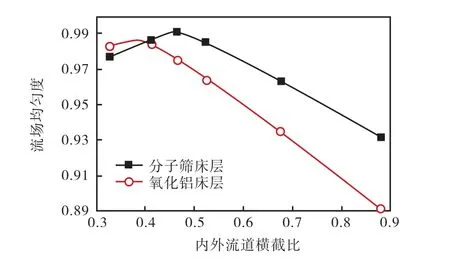
图6 脱附过程中两床层中流场均匀度随内外流道横截比的变化Fig.6 Changes of flow uniformity in two beds along with the cross-sectional area ratio of the inside to outside flow channels during desorption process
图7为最佳横截比时两流道内和床层之间的静压力.内外流道横截比减小,中心流道直径变小,气速增大摩擦阻力增大,引起的静压力降增加,由原来的约50,Pa变为100,Pa左右;而环形变宽,气速降低,摩擦力减小引起的静压力降也减小,由原来的约150,Pa减小到100,Pa左右.两流道内压降趋同,使得床层两侧压差更加均匀.床层内3个截面上的速度与图3相比,床层内下部速度下降,上部速度升高,使得速度轴向更加均匀,但大体趋势相同.达到最佳横截比后,继续增加内外流道横截比,床层内气流均匀度下降,其原因与吸附过程类似,中心流道内压降超过环流道内压力降,使得床层上部压差大于下部,从而床层均匀度变差.

图7 脱附过程中n=0.414时内外流道及两流道之间的静压力轴向分布Fig.7 Axial static pressure distribution of the inside,outside and middle flow channels during desorption process when n=0.414
在吸附和脱附过程中,若要增大两床层内气体分布均匀度,则需要分别增大或减小内外流道横截比.然而两者不能同时达到,只能相互折中,再通过其他办法进一步提高两个过程的轴向气流均匀度.
3.3 床层空隙率对气流均匀度的影响
吸附过程中,降低分子筛空隙率,分子筛和氧化铝床层气流均匀度均有大幅度提升;降低氧化铝床层空隙率,分子筛床层流场均匀度有所提高,但氧化铝床层流场均匀度先稍微下降后有所上升,具体数值见表3.分析其原因,床层空隙率的降低增加了气体流通的阻力,尤其是在原来气流速度较快的地方,阻力增加更大,迫使流体向流通阻力更小的地方流动,使得气体的流量在床层的各个高度处分布更加均匀.但在吸附过程中,氧化铝床层在外侧且其厚度较薄,气流进入时压降波动较大,如图8中的方格曲线下部压降有明显的波动,但当它的空隙率降低时,下部波动变小,这样一来使得自身床层均匀度稍有下降,继续降低其床层空隙率其气流均匀度又开始呈上升趋势.

表3 吸附及脱附过程床层均匀度随床层空隙率的变化Tab.3 Changes of bed uniformity along with bed void fraction during adsorption and desorption processes

图8 吸附过程中不同床层空隙率的归一化氧化铝床层压力降变化Fig.8 Changes of normalized alumina bed pressure drop along with different bed void fractions during adsorption process
在脱附过程中,气体先进入分子筛床层,其床层厚度较大,压降并不存在波动,所以气流均匀度随床层孔隙率的降低呈不断上升趋势.但对于分子筛床层来说,降低分子筛空隙率,气流均匀度提高更大;而对于氧化铝床层来说,降低氧化铝空隙率,气流均匀度提高更多.因为降低床层空隙率时,该床层自身压力降增加,对自身压降的轴向差异削弱更大,即压降的基数更大,差异相对减小,所以均匀度上升较多.
分子筛床层较厚,其空隙率降低带来较大压降,当空隙率降到0.3时,在吸附过程中,高10,m处带来了2,000,Pa的额外静压力,如图9所示;在脱附过程中,高7,m处带来了约1,000,Pa的压力增加,如图10所示;但氧化铝较薄,其空隙率的降低带来的压力降也相对较小.

图9 吸附过程不同床层空隙率、x=10,m处静压力沿y轴分布Fig.9 Static pressure distribution along y axis at x=10,m with different bed void fractions during adsorption process

图10 脱附过程中不同床层空隙率、x=7,m处静压力沿y轴分布Fig.10 Static pressure distribution along y axis at x=7,m with different bed void fractions during desorption process
3.4导气锥对气流均匀度的影响
导气锥是一种常用的增加气流分布均匀性的分布器,它能使得中心流道横截面积随高度变化进而减小气流速度的变化,降低气速变化引起的压力降,同样也起到改变内外流到横截比的作用.这里在原来的纯化器物理模型中加一个高HZ为14,m、底面圆半径Rd为0.68,m的导气锥,其尺寸根据工业数据选取.本文对加装导气锥的纯化器进行模拟时,所采用的数学模型、边界条件及网格尺寸与前文一致.
表4给出加入锥体前后吸附脱附两过程床层均匀度数据,发现加入锥体后吸附过程两床层均匀度稍微有所下降,而脱附过程两床层均匀度都有大幅度上升.加入锥体减小了中心管的流通截面积,相当于在原尺寸的基础上减小内外流道横截比.与前文所得结论相似,吸附过程两床层均匀度下降,脱附过程两床层均匀度上升,但又由于锥体下部粗上部细,起到调节动量因素对静压力的影响,因而使得吸附过程两两床层流场的均匀度下降幅度很小,而脱附过程中两床层流场均匀度有很大提高,且脱附再生越完全,吸附效果越好,锥体起到了很积极的作用.

表4 导气锥对纯化器床层内气流均匀度的影响Tab.4 Influence of cone distributor on airflow uniformity in clarifier bed
3.5多因素对流场均匀度影响分析
前面讨论了单因素对吸附和脱附过程中床层流场均匀度的影响,为进一步更有效率地提高床层流场均匀度,这里讨论一下多个因素叠加对流场均匀度的影响.由于内外流道横截比对吸附和脱附两个过程床层均匀度的影响方向是相反的,只能择中选取,这里不作变动,只适当改变两床层空隙率并同时加入导气锥分析其所得床层内气流均匀度.表5给出了不同床层空隙率以及是否有导气锥时,两床层均匀度的结果.
在吸附过程中,同时降低两床层空隙率并加入锥体,对吸附过程两床层均匀度均有提高,但效果没有单纯降低分子筛床层空隙率到0.33得到的结果理想.但在脱附过程中,同时降低两床层空隙率并加入锥体,得到的两床层均匀度的结果要好于任何单因素的影响,甚至好于把分子筛空隙率降低到0.30所得到两床层的均匀度.

表5 多因素对床层内气流均匀度的影响Tab.5 Influence of many factors on the airflow uniformity in bed layer
多因素同时改变时,两床层某一高度处的静压力如图11和图12所示,降低分子筛和氧化铝空隙率分别到0.33和0.35,并加入锥体,在吸附过程中带来约1,300,Pa的床层压力降的增加,与单纯降低分子筛空隙率到0.33带来的床层压力增加相差不多;在脱附过程中,3因素叠加带来了约500,Pa的床层压力降的增加,远小于单纯降低分子筛空隙率到0.30所带来的1,000,Pa左右的床层压力增加.
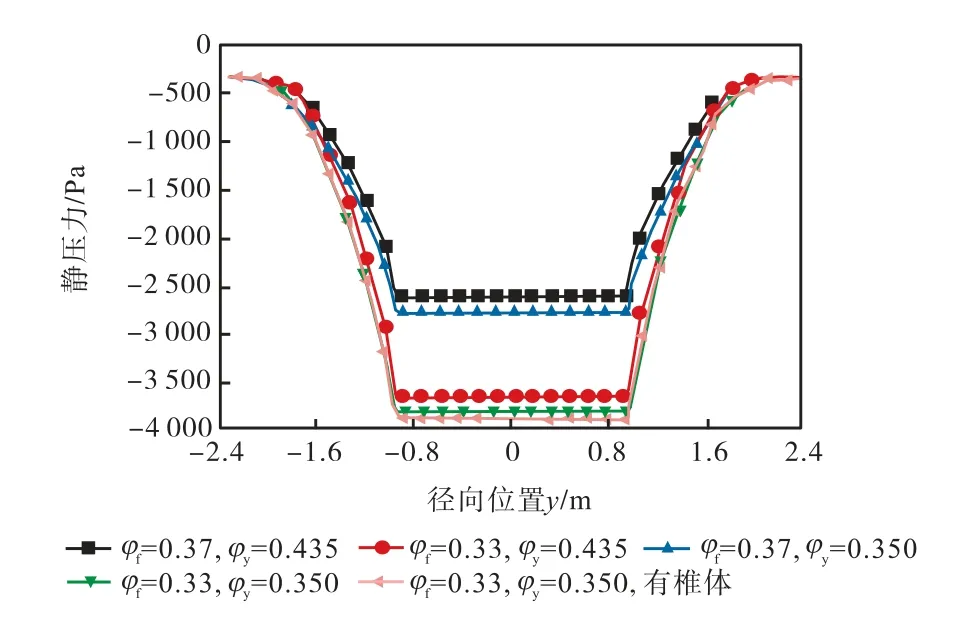
图11 吸附过程中不同条件下x=10,m处静压力沿y轴的分布Fig.11 Static pressure distribution along y axis at x=10,m in different conditions during adsorption process

图12 脱附过程中不同条件下x=7,m处静压力沿y轴的分布Fig.12 Static pressure distribution along yaxis at x=7,m in different condition during desorption processs
综合吸附和脱附过程,同时降低两床层空隙率并加入锥体,对吸附过程两床层均匀度均有提高,效果比单纯降低分子筛床层空隙率到0.33稍差.但在脱附过程中在较小的床层压降增加的基础上极大地提高了两床层均匀度,而且在工业生产过程中脱附过程比吸附过程对床层气流均匀度要求更苛刻.所以在本文的讨论范围内,同时小幅度降低两床层空隙率并加入锥体,对于改善纯化器内气流均匀度是最理想的.
4 结 论
(1)在纯化器吸附过程中,床层内轴向气流均匀度随着内外流道横截比的变大呈先变大后变小的趋势,内外流道最佳横截比为0.887.在脱附过程中,分子筛和氧化铝床层气流均匀度都随着内外流道横截比的降低先增大后下降,均匀度在内外流道横截比为0.47和0.38左右分别达到最大值.
(2)在纯化器吸附过程中,降低氧化铝床层的空隙率,对自身流场均匀度有先变小后变大的趋势,对分子筛床层流场均匀度稍有提高,而降低分子筛床层空隙率,两床层流场均匀度都有明显提高;在脱附过程中,两床层空隙率的降低对两床层均匀度都有提高.
(3)在纯化器中心流道加入导气锥会使吸附过程床层气流均匀度稍有下降,但是可以使脱附过程中床层内气流均匀度有较大上升.加入导气锥,一方面相当于缩小了内外流道横截比,另一方面又减小了气流速度的变化对两床层均匀度的影响,两者综合使得床层均匀度在吸附过程中减小不大,在脱附过程增加较多.
(4)本文提出最优的提高气流均匀度的方案如下:同时降低分子筛和氧化铝床层空隙率到0.33和0.35,并加入锥体.对吸附过程两床层均匀度均有提高,且在脱附过程中在较小的床层压降增加的基础上两床层均匀度提高到很理想的状态,满足了脱附过程对床层均匀度的苛刻要求.
参考文献:
[1]陆军亮,张学军,邱利民,等.立式径向流吸附器中流体均布的理论分析[J].化工学报,2012,63(S2):21-25.Lu Junliang,Zhang Xuejun,Qiu Limin,et al.Theoretical analysis of uniform flow distribution in vertical radical adsorption bed[J].CIESC Journal,2012,63(S2):21-25(in Chinese).
[2]Lobanov E L,Skipin Y A.Increasing the operating efficiency of radial reactors in reforming[J].Chemistry and Technology of Fuels and Oils,1981,22(6):275-278.
[3]Suter D,Bartroli A,Schneider F,et al.Radial flow reactor optimization for highly exothermic selective oxidation reactions[J].Chemical Engineering Science,1990,45(8):2169-2176.
[4]宋续祺,汪展文,金 涌,等.移动床径向反应器中流体力学行为的研究[J].化工学报,1992,43(3):268-274.Song Xuqi,Wang Zhanwen,Jin Yong,et al.The research of the fluid mechanics behavior of the moving bed radial reactor[J].CIESC Journal,1992,43(3):268-274(in Chinese).
[5]Heggs P J,Ellis D I,Ismail M S.The modeling of fluidflow distributions and pressure changes in multilayered annular packed beds[J].Gas Separation and Purification,1994,8(4):257-264.
[6]Heggs P J,Ellis D I,Ismail M S.Prediction of flow distributions and pressure changes in multi-layered annular packed beds[J].Gas Separation and Purification,1995,9(4):243-252.
[7]Kareeri A A,Zughbi H D,Al-Ali H H.Simulation of flow distribution in radial flow reactors[J].Industrial and Engineering Chemistry Research,2006,45(8):2862-2874.
[8]Mu Z,Wang J,Wang T,et al.Optimum design of radial flow moving-bed reactors based on a mathematical hydrodynamic model[J].Chemical Engineering and Processing:Process Intensification,2003,42(5):409-417.
[9]Manjhi N,Verma N,Salem K,et al.Simulation of 3D velocity and concentration profiles in a packed bed adsorber by lattice Boltzmann methods[J].Chemical Engineering Science,2006,61(23):7754-7765.
[10]李瑞江,陈春燕,吴勇强,等.大型径向流反应器中流体均布参数的研究[J].化学工程,2009,37(10):28-31.Li Ruijiang,Chen Chunyan,Wu Yongqiang,et al.Parameters for uniform distribution of stream in large-scale radial flow reactors[J].Chemical Engineering,2009,37(10):28-31(in Chinese).
[11]Li R,Zhu Z.Investigations on hydrodynamics of multi
layer Π-type radial flow reactors[J].Asia-Pacific Journal of Chemical Engineering,2012,7(4):517-527.
[12]Ergun S.Fluid flow through packed columns[J].Chem Eng Prog,1952,48:89-94.
[13]Choudhury D.Introduction to the Renormalization Group Method and Turbulence Modeling[R].Technical Report TM-107,Fluent Incorporated Technical Memorandum,1993.
(责任编辑:田 军)
Simulation and Analysis on Gas Flow Distribution in Radial Flow Air Adsorber
Tang Zhongli1,2,Xu Mingyang1,2,Zhang Jun1,2
(1.School of Chemical Engineering and Technology,Tianjin University,Tianjin 300072,China;2.State Key Laboratory of Chemical Engineering(Tianjin University),Tianjin 300072,China)
Abstract:Gas flow distribution and its influence factors in a eighty thousand tons adsorber have been investigated by computational fluid dynamics(CFD).It is found that the axial uniformity of the flow distribution can be maximized when the cross-sectional area ratio of the center pipe to the annular channel reaches a certain value in adsorption process and desorption process.The uniformity in the two layers can both be improved by lowering the porosity of molecular sieve layer.In addition,a cone distributor can cause a little decrease of the uniformity in adsorption process,but can cause a relatively large increase in desorption process.An optimal solution is proposed as follows:Adjusting the porosity of the inner molecular sieve layer and the alumina layer to 0.33 and 0.35,respectively;Adding a cone distributor,the uniformity in the two layers can be improved with a slight increase of the pressure drop in both adsorption and desorption processes.
Keywords:air separation;radial flow;gas flow distribution;structure optimization;CFD simulation
通讯作者:唐忠利,zltang@tju.edu.cn.
作者简介:唐忠利(1969—),男,博士,副教授.
收稿日期:2014-10-31;修回日期:2014-12-26.
DOI:10.11784/tdxbz201410080
中图分类号:TQ
文献标志码:A
文章编号:0493-2137(2016)03-0305-09
网络出版时间:2015-01-07.网络出版地址:http://ww.cnki.net/kcms/detail/12.1127.N.20150107.1035.001.html.

