基于HMM的主题爬虫问题研究
曹琨
(新乡学院计算机与信息工程学院,河南 新乡 453000)
基于HMM的主题爬虫问题研究
曹琨
(新乡学院计算机与信息工程学院,河南 新乡 453000)
对HMM爬虫中K-means算法的K值选取方法作出相应改进,然后针对爬取网页的内容与主题相关度不高的问题,对隐马尔科夫模型的假设条件进行修改,完成改进后的隐马尔科夫爬虫设计。
网络爬虫;算法;改进
隐马尔科夫模型(Hidden Markov Model,HMM)应用比较广泛。最初应用于通信工程领域,进行信号处理,之后被应用到自然语言处理方面,成为自然语言处理和通信系统联系的纽带;再到后来,机器学习比较流行,开始用隐马尔科夫模型。该模型用于机器学习时,主要用鲍姆-韦尔奇训练算法。HMM是一种具有统计特性的随机过程概率模型,在该模型中参数表示尤为重要,并且是由马尔科夫链和一般随机过程组成。本文主要利用马尔科夫链的随机过程模型对网络爬虫予以改进。
1 HMM主题爬虫框架
将HMM引入到主题爬虫后,增加了爬虫对网页主题的识别能力,使用训练好的HMM可以很好地预测爬取路径。但是,经过对隐马尔科夫数学模型和基于隐马尔科夫主题爬虫的理论进行分析研究,可以发现在传统的HMM模型中有部分不合理的地方。
HMM爬虫运行主要有3个阶段:①初始阶段,对相关参数进行设置,选定初始网页初始训练集,进行页面预处理等;②学习阶段,对网页进行文本相关度计算、类型聚类和构建隐马尔科夫模型训练优化;③运行阶段,用优化后的隐马尔科夫模型对查找到的主体相关的站点进行分析,主要包括网页内容相关度判断和超链接分析处理,将分析结果储存起来,根据网址路径爬取网页到本地服务器。
经过研究发现,传统的隐马尔科夫模型爬虫存在以下几个缺点:①和一些经典爬虫算法相比,HMM爬虫时间消耗较大,其建模方法和算法有待改进;②在HMM爬虫抓取的网页中,主题相关度还有待提高;③对训练集处理过于简单,影响了爬行过程精确度,导致主题相关度降低很多。
2 改进HMM模型聚类策略
网页数据聚类是将网页数据按照相似性进行分类的过程,不同类中的网页对象有很大的相异性。具体过程是:首先需要一个给定的分类体系和训练样本集,如“天眼舆情分析系统”中的中文网页分类体系,其将所有网页分为15个大类,即任何网页都可以根据内容归属到某一类样本,这种利用已标记样本集对未知样本进行类别划分的方法称作“有监督的学习方法”[1]。
K-means算法对网页进行聚类的主要思想是认为两个链接越近的网页其相似度越大,这一思想看似简单,但要确定划分类别的数量K,同类的相似度高,不同类的相似度低。通常K的值是用户给定的,而K值大小对爬虫抓取的效率和准确度有很大的影响,很多用户难以确定K值的大小。目前,很多学者致力于K值获取方法的改进研究,比如利用图论、距离代价函数和遗传算法等。
3 改进HMM模型页面采集方法
3.1 页面与主题相关度判定
在传统的HMM爬虫系统中,采用空间向量模型(VSM)进行网页主题相关度计算,通过计算用户给出的关键字在当前页面中的权值来判断与页面相关度,关键字出现在页面中的位置也是衡量权值的重要因素。
将网页页面分成4个部分:页面标题、副标题、重点强调文字和普通正文。权重分配如下:
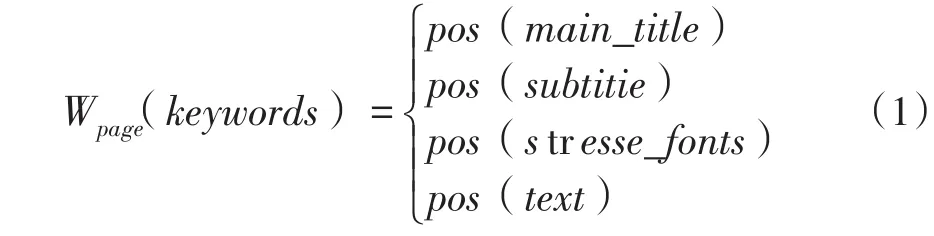
例如,关键字“Apple”在某个网页P的主标题中出现了1次,正文中出现了5次,且强调字体出现3次,那么关键词“Apple”在网页P中的权重计算方法为:
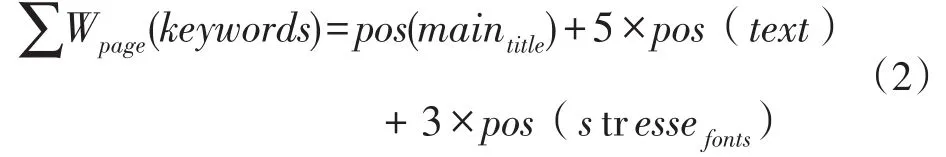
3.2 HMM爬虫建模方法改进
HMM爬虫基本工作原理是根据页面与查询主题的相关度来抓取网页,如果相关则抓取,并且提取储存此网页的链接地址。如果不相关就舍弃,读取下一个网页。此方法最大弊端就是爬虫经过判断丢弃了不相关网页,而这些网页中有可能存在着指向与主题相关度很高的超链接,这个问题使爬虫丢失了部分有价值的页面。这与HMM的假设条件和算法的不合理有关。HMM中存在如下2个假设。
假设1:系统状态从t时刻向t+1时刻转移时,其转移概率只与t时刻状态有关,与历史状态无关,即:
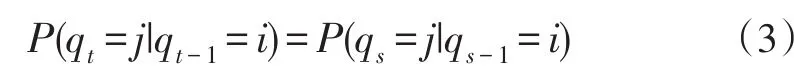
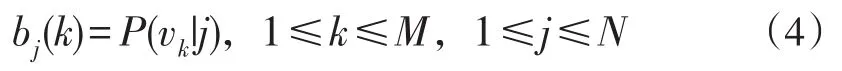
假设2:系统在时刻t输出观察值的概率只取决于当前时刻1所处的状态而与之前的状态无关,即:由于上述假设将网页之间的链接关系割裂了,所以处理网页之间的关系并不合理,如果和主题相关的网页指向该网页的概率大,那么就认为这个网页上的链接也有很大的概率指向该网页。为了挖掘出页面当前状态与历史状态之间的联系,对上文两个假设进行如下修改。
假设1:系统状态从t时刻向t+1时刻转移时,其转移概率依赖于t和t-1时刻的状态,即:
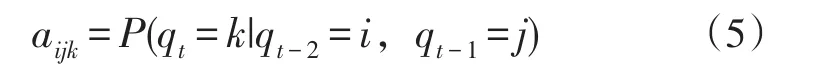
假设2:系统在时刻t输出观察值的概率取决于系统当前状和系统前一时刻的状态,即:
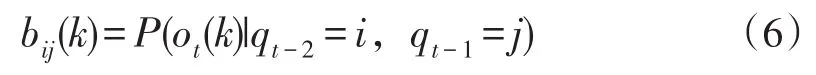
本文在假设条件(5)和(6)的基础上对HMM的学习算法Forward和Backward算法进行了改进,此算法是在模型λ下计算产生观察序列O=O0,O1…,Oi的概率,即P(O|λ)。
3.2.1 Forward算法。首先定义Forward变量∂,如式(7)所示:
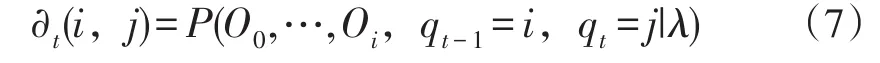
式(7)中,∂t(i,j)表示在模型λ中,时刻为t时,部分观察值序列为P(O0,…,Oi)的概率。Forward变量∂t(i,j)可以递归求解,步骤如下:
3.2.2 Backward算法。类似地定义Backward变量β,如式(8)所示:
式(8)中,1<t<T-1,0<i,j<N-1,Backward变量β(i,j)递归求解步骤如下:
初始化:βT-1(i)=1,0<i,j<N-1;
迭代:βt(i,j)=
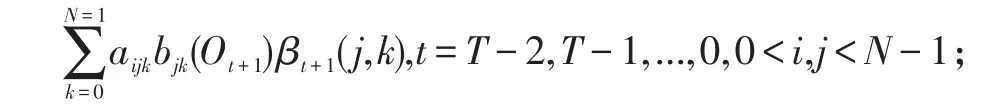
由此,根据Forward-Backward算法,在给定模型的情况下,产生观察值序列的概率为:
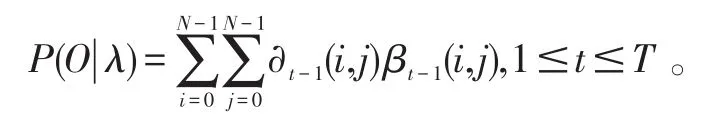
4 结语
在传统HMM爬虫的基础上,对K-means算法中的K值的设置方法做了改进。首先,通过训练集聚类策略,解决了用户通过经验来定义K值带来的诸多问题;其次,在传统的方法上优化了相关度的判别统计方法;最后,针对HMM爬虫爬取来的网页与主题相关度不高的问题,对两个假设条件进行了修改,从而改进了HMM的建模方式。
[1]李光敏.文献搜索引擎中特征项及权重的应用[J].计算机系统应用,2014(5):188-191.
Research on Topic Crawler Based on HMM
Cao Kun
(School of Computer and Information Engineering,Xinxiang College,Xinxiang Henan 453000)
This paper made corresponding improvement on K value selection method of K-means algorithm in HMM crawler,then aiming at the problem that the correlation between the content and theme of the crawled page is not high,improved the assumed condition of the hidden Markov model,and completed the improved hidden Markov crawler designing.
network crawler;algorithm;improvement
TP391.3
A
1003-5168(2016)09-0027-02
2016-08-20
曹琨(1983-),女,讲师,硕士,研究方向:计算机科学与技术。

