多发多收探测雷达定位精度分析

郭文玲　李雪　李吉宁　鲁转侠　曹红艳

(中国电波传播研究所,青岛 266107)



多发多收探测雷达定位精度分析

郭文玲李雪李吉宁鲁转侠曹红艳

(中国电波传播研究所,青岛 266107)

摘要多发多收是提高雷达系统定位精度的重要手段之一,为分析不同形式多发多收定位精度,采用二维定位几何精度稀释分析方法,分别针对两发两收、两发四收和三发三收三种探测方式进行了仿真分析.结果表明:两发四收探测系统定位精度比两发两收系统整体上提高,在基线近区提高比较明显;三发三收探测系统克服了两发两收探测系统在基线上定位盲区的缺点,但与两发四收探测系统相比,除基线附近外，在三站围成的定位区域内定位性能并没有明显提高.仿真结果为多发多收探测系统选取、布站提供了理论参考,具有一定的工程应用价值.

关键词多发多收;雷达;几何精度稀释

DOI10.13443/j.cjors.2015020702

The positioning accuracy analysis of multi-transmit multi-receive detection radar

GUO WenlingLI XueLI JiningLU ZhuanxiaCAO Hongyan

(ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China)

Abstract Multi-transmit multi-receive (MTMR) is an important mean to improve the positioning accuracy of the radar system. To analyze the positioning accuracy of different MTMR systems, we use two-dimensional positioning GDOP analysis method to simulate the systems of two-transmit two-receive, two-transmit four-receive and three-transmit three-receive (2T2R, 2T4R, 3T3R). The results show that: compared with the 2T2R, the positioning accuracy of the 2T4R system is overall improved and the improvement much more obviously in the near baseline zone; the 3T3R overcomes the defects of the 2T2R that has positioning blind zone on the baseline, however, compared with the 2T4R, positioning accuracy of the region rounded by the three stations is not obviously improved except in the near baseline zone. The simulation results provide theoretical reference in MTMR detection system selection and radar station deployment,and thus is valuable to radar configuration applications.

Keywords multi-transmit multi-receive; radar; GDOP

引言

多发多收雷达具有良好的抗电子干扰、抗超低空突防、抗反辐射导弹、抗隐身武器的能力,是目前雷达领域研究的重点之一[1]. 由于收发分离,发射机可部署在远离战场的安全部位,接收机无源工作,可部署在战区的前沿,增强了抗有源干扰和抗反辐射导弹能力. 同时通过多发多收组成雷达网,不仅扩大了雷达的覆盖范围,提高发现能力和定位精度,对隐身目标探测[2]也是一种有效的技术途径. 多发多收雷达的不同探测系统和设备探测能力对系统的定位精度都有很大影响.

目前,对多发多收雷达定位性能进行的研究主要集中在以下三个方面:第一,基于测向定位,文献[3]以测向定位为基础对定位误差与雷达布站的关系进行了分析;第二,基于测距定位,文献[4]对基于纯测距的距离和的多基地雷达定位进行了研究;第三,基于测向和测角的联合定位,文献[5]基于双/多基地雷达的仰角、方位角与距离等参量的联合探测对目标进行定位.

基于测向的目标定位方法,角度误差对定位精度影响较大[6]. 对某些波长较长的探测系统,如超短波雷达、高频雷达等,其方位分辨率通常较低,为获得高的方位分辨率通常需要配备大规模的天线阵,代价较高. 基于距离的目标定位方法,距离的测量精度相对较高,但是两发两收的两站探测系统定位精度有限,基于距离和的一发多收的多基地定位,至少需要选取3个站址. 针对该类探测系统存在的问题,本文提出一种基于距离定位的两发四收探测体制,该体制不仅降低系统规模,提高定位精度,同时还避免单站雷达切向盲速问题．如图1所示,探测系统布置在A、B两地,两地分别有发射设备和接收设备,接收设备可接收A、B两地的发射信号. 这种探测体制只需选取两个探测站,降低了多个站址选取的难度.

图1　两发四收探测体制示意图

1探测系统定位精度理论分析

1.1定位精度分析方法

几何精度稀释(Geometrical Dilution of Precision, GDOP)[7]是衡量定位系统性能的重要指标之一,是定位误差均方根与测距误差均方根的比值,当他们单位相同时,无纲量,反映了布站系统对探测点的定位性能. 测距误差相同的情况下,GDOP越小,定位性能就越好. 文献[8]通过对多基地雷达不同布站方式GDOP的分析,得出要提高定位精度,应在扇形交替布站情况下,增加接收站数量的结论. 文献[9]通过对定位系统GDOP的分析得出最优定位点位置的关系式.

本文也以GDOP为系统定位性能的评估依据，对基于距离定位的两发两收、三发三收和两发四收探测体制定位性能进行仿真分析.

雷达定位性能受雷达站址误差、随机测量误差和雷达网时间同步误差的影响. 其中站址误差小于10 m[10],时间同步误差小于1 μs,相比于测距误差,这两个误差影响比较小,可以暂不考虑.

设定所有的距离测量是相互独立的,探测站的测量误差均值为零,误差标准差都为σr.

以A、B两探测站连线为x轴,两站间的中垂线为y轴,y轴的正方向指向雷达的探测区域建立直角坐标系. 设目标坐标为(x,y),雷达探测站坐标为(xi,yi),探测站测得的距离为Ri.

对于两维定位系统,其GDOP表达式为[11]

(1)

式中: σx表示在x轴方向上的定位误差标准差; σy表示在y轴方向上的定位误差标准差.

基于距离定位的两发两收和三发三收探测系统获取的探测信息为

(2)

N=2时表示两发两收探测系统,N=3时表示三发三收探测系统．定位精度表示为[12]

(3)

式中,

G=(HTQ-1H)-1,

(4)

Q为探测站测距误差协方差矩阵,N=2时,

(5)

N=3时,

(6)

(7)

对于本文提出的两发四收探测体制,有A、B两个探测站,4条探测路径,获取的距离信息如式(8)和式(9)所示:

(8)

(9)

此时,

(10)

即

(11)

探测站测距误差协方差矩阵为

(12)

1.2定位精度仿真结果

仿真研究中,设定两探测站相距320km,探测区域为x轴上-160km到160km,y轴上0km到300km. 假设各个探测站的距离测量误差是相互独立的,距离测量误差均值为零,均方根误差为1km,

即

σr=1.

(13)

两发四收与两发两收探测系统GDOP对比如图2所示. 由图2(a)可知两发四收探测系统定位性能优于两发两收探测系统,特别是在距离基线100km附近,如图2(b)所示,定位性能提高较大. 两发四收的最小GDOP为1.1,而两发两收最小值为1.5.

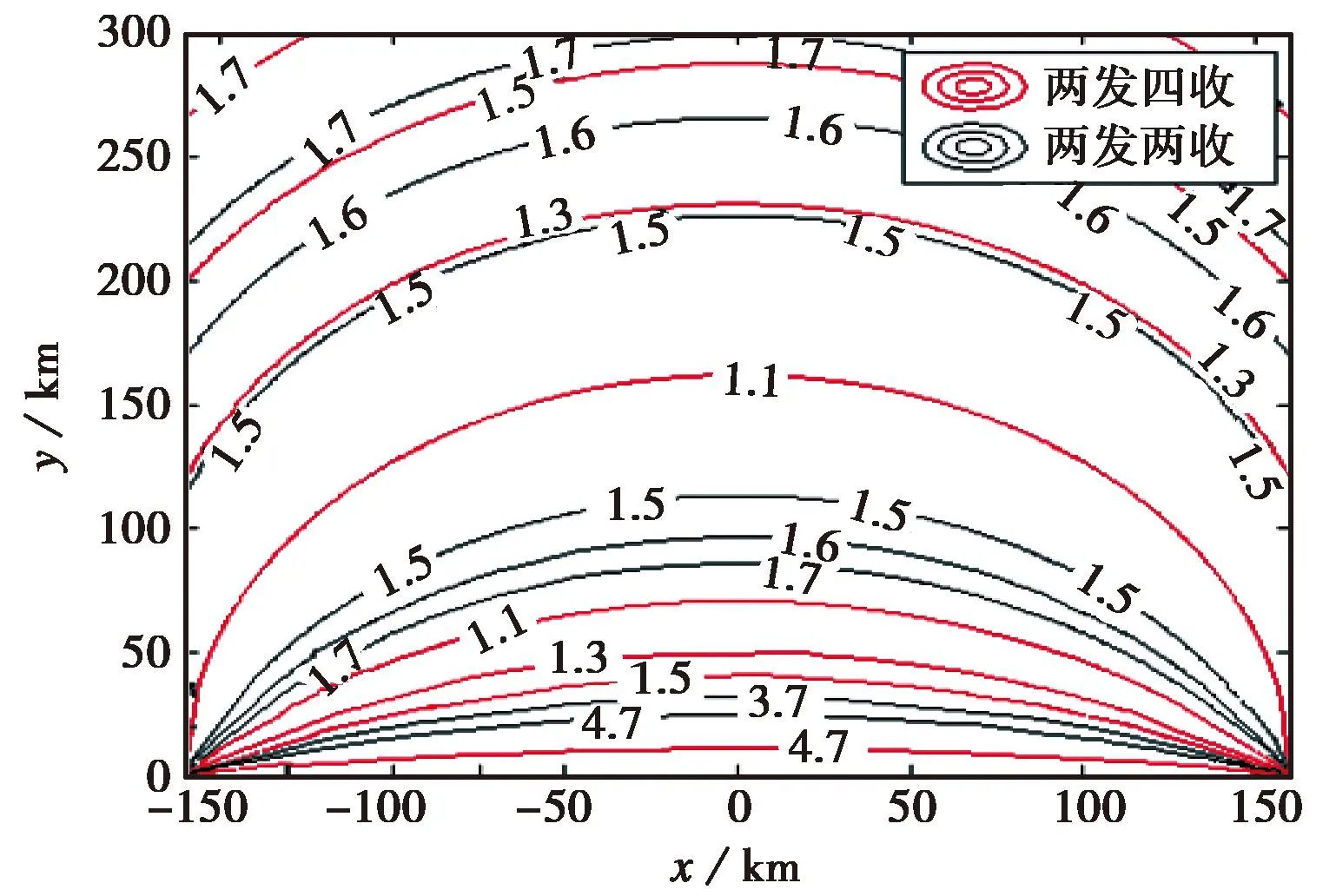
(a) 探测区域GDOP对比

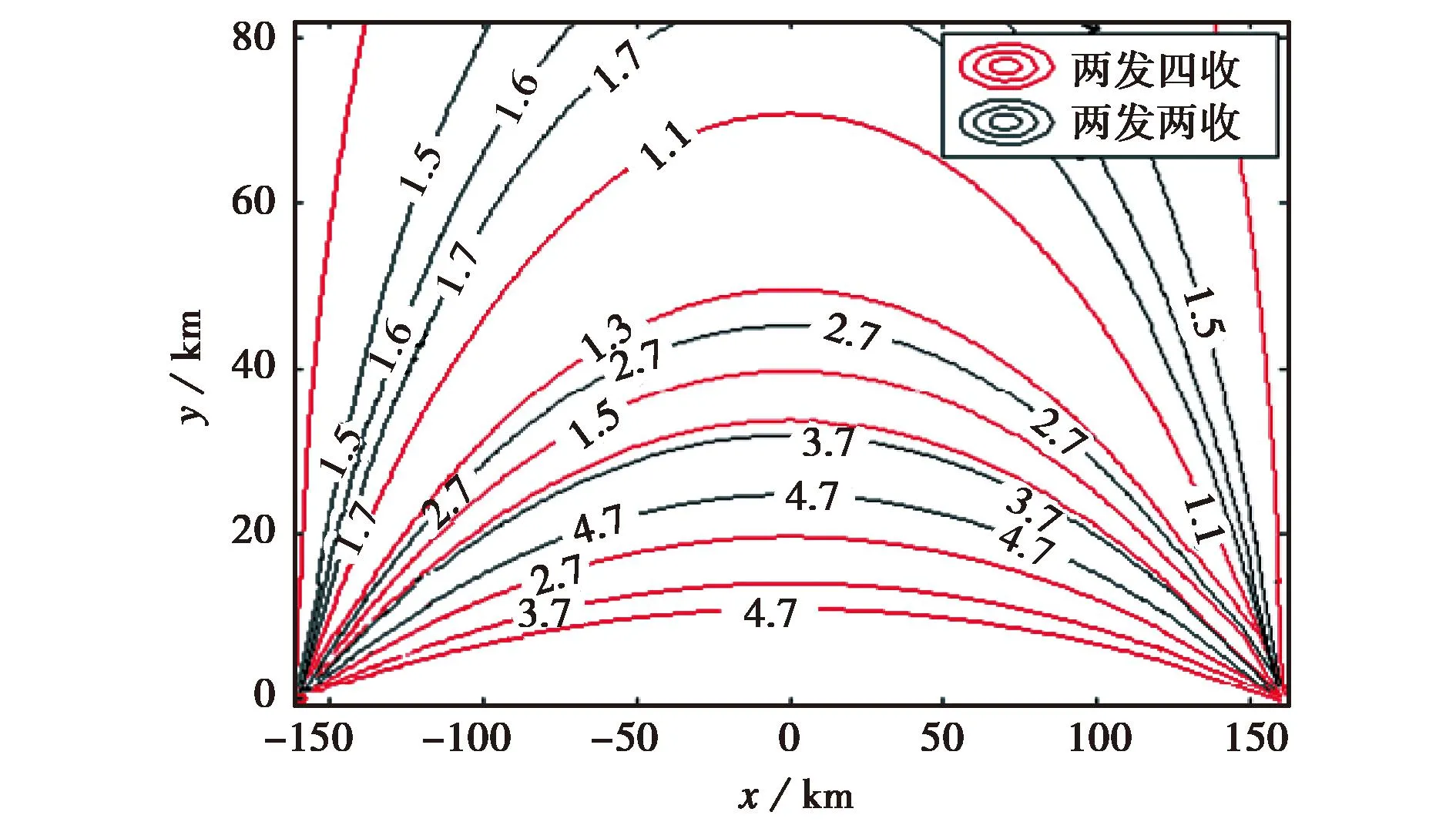
(b) 探测区域近区GDOP对比图2　两发四收与两发两收探测体制GDOP对比

对于三发三收的三站探测,当三站按正三角形布站时三站围成区域内的定位性能最好[13]. 本文选用三站最佳布站,正三角形布站进行仿真,其中两个探测站分布与两发四收的相同,第三个探测站设置在两发四收的两个站的正前方(即坐标y>0).

两发四收与三发三收探测系统GDOP对比如图3所示. 把三发三收探测系统三站围成的区域定义为探测区域. 三发三收探测系统相比于两发四收探测系统消除了探测站基线上的定位盲区. 三发三收系统的最小GDOP为1.2,两发四收系统的最小GDOP为1.1. 在探测区域内除了两发两收探测系统基线附近GDOP低于三发三收探测系统,其余区域两探测系统的定位性能相当,GDOP都在1.4以内,而且两发四收探测系统的最佳定位区要大于三发三收探测系统．在实际应用中,探测区域要距离基线一定的距离,因此从实际应用角度讲,两发四收探测系统的定位性能要高于三发三收系统,同时相比于三发三收探测系统所需站址减少,降低了探测站站址的勘选难度.

图3　两发四收与三发三收探测系统GDOP

2基于假定航迹的定位精度仿真验证

基于距离定位的两发两收探测体制的定位可根据获取的距离信息直接求取交点.

对于三发三收和两发四收探测体制,应用文献[14]中的牛顿迭代算法进行定位. 牛顿迭代算法的一个关键技术是迭代初始值的选取.

对三发三收探测体制,初始值选取两个圆交点,当没有交点时,选取探测区域内一点作为初始值(一般取探测区域的中心点).

对两发四收探测体制,初始值选取两个圆和一个椭圆的三个交点的平均值,当测量误差较大时可能出现达不到三个交点的情况甚至没有交点,对这种现象初始值按以下规则进行选取:

●如果有三个交点,求取三个交点的平均值作为迭代初始值;

●如果只有两个交点,求取两个交点的平均值作为迭代初始值;

●如果只有一个交点,把这点作为初始值;

●如果没有交点,则假定探测区域内的某一点(一般取探测区域的中心点)作为迭代的初始值.

假设各个探测站的距离测量误差均值为零,均方根误差为1km.

对三种探测体制根据定位算法进行定位分析.对两发四收和三发三收探测体制迭代定位时,每个定位点进行10 000次蒙特卡洛计算.

假定三条定位航迹,在三种探测体制下分别进行定位均方根误差的比较,三条航迹如下所示:

航迹一:x=0,y为40km到250km;

航迹二:y=0.7*x+100,其中x∈[-100,100];

航迹三:x∈[-100,100],y=100．

三条航迹分布如图4所示,图中黑色箭头表示目标航迹航行方向.

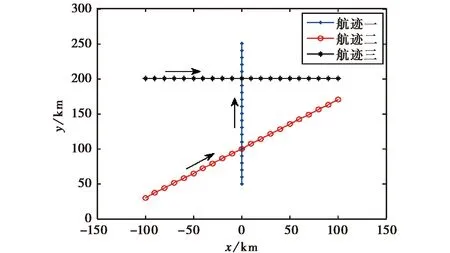
图4　三条航迹示意图

三种探测体制下,三个目标航迹的定位均方根误差分布如图5(a)、(b)和(c)所示.

(a) 航迹一

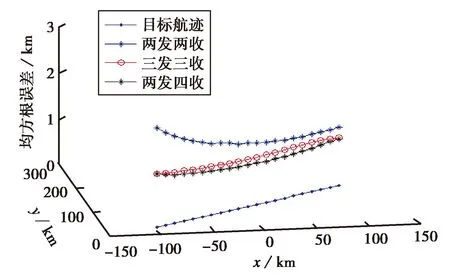
(b) 航迹二

(c) 航迹三图5　三种探测体制下定位误差均方根比较

表1所示为假定的三条航迹上定位点在三种探测体制下的定位误差均值.由表1可知:三发三收探测体制下定位误差比两发两收探测体制下定位误差至少小0.3km;两发四收探测体制下定位误差比三发三收探测体制下定位误差小0.1km左右. 可见,两发四收探测系统定位误差最小,两发两收探测系统定位误差最大.

表1　航迹定位误差均值比较

由分析可知,各个探测系统的定位均方根误差与GDOP变化趋势相符. 两发四收探测系统的定位精度最好,三发三收探测系统的定位精度次之,两发两收探测方式的定位精度最差.

3多发多收实验数据验证

为了进一步验证理论仿真正确性,开展了民航探测试验,探测设备分别布置在相距40km的A、B两地,两站设有一个发射设备两个接收设备,其中两个接收机分别接收本地发射信号和另一探测站发射信号,构成了两发两收和两发四收探测系统. 其中,系统发射功率为1kW、带宽为80MHz、工作频率分别为26.5MHz、27.3MHz,采用中断线性调频信号,利用AirNav接收设备获取民航目标的真实地理位置.

在上述试验布站方案下,试验获取某航班真实航迹(AirNav数据)在GDOP分布中的位置如图6所示. 由图可知,本航班航迹所在区域定位性能较好. 分别采用两发四收和两发两收探测系统对上述航班进行定位,航班航迹定位对比如图7所示. 其中,两发两收探测系统定位误差均值为3.15km,两发四收探测系统定位误差均值为2.66km,两发四收探测系统定位精度高于两发两收探测系统.

图6　某航班航迹在GDOP图中位置

图7　试验某航班航迹定位对比图

4结论

基于测距定位系统中本文提出的两发四收探测体制与两发两收和三发三收两种探测系统进行了GDOP仿真分析,两发四收探测系统与两发两收探测系统相比,探测区域定位性能提升;与三发三收探测系统相比除基线外,在三站围成区域内定位性能相当. 在对假定的典型航迹进行定位均方根误差分析可知,两发四收探测体制的定位性能最好. 总之,本文提出的两发四收探测体制可以在两发两收探测系统布站的情况下达到三发三收探测体制的定位精度,它既提高了两发两收探测系统的定位精度又降低了三发三收探测系统的三个探测站站址的勘选问题,试验数验证了仿真理论的正确性.

本文研究内容为多发多收探测系统的选取和布站提供理论参考,具有一定的工程应用价值.

参考文献

[1]李学勇. 双/多基地雷达发展及关键技术[J]. 雷达与对抗, 2013, 33(2): 4-8.

LIXY.Developmentandkeytechnologiesofbistatic/multistaticradars[J].Radar&ECM, 2013, 33(2):4-8.(inChinese)

[2] 张建新, 张永顺, 曲靖华. 双/多基地雷达反隐身定位分析[J]. 弹箭与制导学报, 2006, 26(2): 987-988.

ZHANGJX,ZHANGYS,QUJH.Analysisofcounter-stealthpositioninginbistaticormultistaticradar[J].Journalofprojectiles,rockets,missilesandguidance, 2006, 26(2): 987-988.(inChinese)

[3] 李兴民, 李国君, 李健, 等. 双站交叉定位雷达布站方法研究[J]. 雷达科学与技术, 2011, 9(5): 405-408.

LIXM,LIGJ,LIJ,etal.Radarconfigurationresearchofdoublestationcrosslocation[J].Radarscienceandtechnology, 2011, 9(5): 405-408.(inChinese)

[4] 冯广飞, 谢军伟, 杨守国, 等. 基于距离和定位的双/多基地雷达定位精度分析[J]. 现代防御技术, 2011, 39(2): 65-68.

FENGGF,XIEJW,YANGSG,etal.Analysisofpositionfindingerrorsbasedonsumofdistancelocationinbistatic/multistaticradar[J].Moderndefencetechnology, 2011,39(2):65-68. (inChinese)

[5] 刘军, 解嘉宇, 郭继周. 多基地雷达马氏定位算法优化[J]. 电讯技术, 2010, 50(7): 97-101.

LIUJ,XIEJY,GUOJZ.OptimizationofMarkovestimationalgorithmformultistaticradarpositioning[J].Telecommunicationengineering, 2010, 50(7): 97-101. (inChinese)

[6] 余洪涛, 张永顺, 齐立峰. 对一种多基地雷达系统定位精度的计算与分析[J].空军工程大学学报:自然科学版,2005,6(4):8-11.

YUHT,ZHANGYS,QILF.Calculationandanalysisofprecisionoflocalizationofamulti-staticradarsystem[J].JournalofAirForceEngineeringUniversity:naturalscienceedition, 2005, 6(4): 8-11. (inChinese)

[7] 孙终康, 周一宇, 何黎星. 单多基地有源无源定位技术[M]. 北京:国防工业出版社,1996: 37-43.

[8] 牛超, 张永顺. 基于GDOP的多基地雷达布站优化研究[J]. 现代防御技术, 2013, 31(3): 117-123.

NIUC,ZHANGYS.SitesdistributionoptimizationmodelofmultistaticradarbyGDOP[J].Moderndefensetechnology, 2013, 31(3):117-123. (inChinese)

[9] 吴魏, 王国宏, 王娜, 等. 双基地雷达定位系统的最优定位点研究[J].现代防御技术, 2010, 38 (2): 89-92.

WUW,WANGGH,WANGN,etal.Optimumlocationpointinbistaticradarlocationsystem[J].Moderndefencetechnology, 2010, 38(2):89-92. (inChinese)

[10]徐宏, 韩壮志, 何强, 等. 自卫式干扰火控雷达网测向交叉定位精度分析[J].火力指挥与控制, 2011, 36(5): 25-28.

XUH,HANZZ,HEQ,etal.Performanceanalysisofdirection-findinglocationorientedtoself-defensejamminginfire-controlradarnet[J].Firecontrol&commandcontrol, 2011, 36(5):25-28. (inChinese)

[11]杨雷明. 信号处理中无源定位的分析与研究[D]. 西安:西安电子科技大学, 2012.

YANGLM.AnalysisofandResearchonPassiveLocationinSignalProcessinginSignalProcessing[D].Xi’an:XidianUniversity, 2012.(inChinese)

[12]LEVANONN.LowestGDOPin2-Dscenarios[J].IEEEproceedingradarsonarandnavigation, 2000, 147(3):149-155.

[13]MANOLAKISDE.Efficientsolutionandperformanceanalysisof3-DpositionestimationbyTrilateration[J].IEEEtransactionsonaerospaceandelectronicsystems, 1996, 32(4): 1239-1248.

[14]杨振起, 张永顺, 骆永军. 双(多)基地雷达系统[M]. 北京:国防工业出版社, 1998: 205-215.

郭文玲 (1986-),女,山东人,硕士,工程师,目前主要研究方向为电离层电波传播、雷达信号处理等.

李雪 (1981-),男,黑龙江人,博士,高级工程师,目前主要研究方向为电离层回波信号处理、雷达信号处理、电波传播等.

李吉宁 (1982-),男,山东人,硕士,工程师,目前主要研究方向为高频超视距雷达、雷达信号处理和电波传播.

鲁转侠 (1978-),女,陕西人,硕士,高级工程师,主要研究方向为天波斜向探测电离层图数值分析、模拟、判读和电离层回波信号处理等.

曹红艳 (1977-),女,河南人,硕士,高级工程师，主要从事短波频率预测方法研究及软件开发.

作者简介

中图分类号TN95

文献标志码A

文章编号1005-0388(2016)01-0047-06

收稿日期：2015-02-07

郭文玲, 李雪, 李吉宁, 等. 多发多收探测雷达定位精度分析[J]. 电波科学学报,2016,31(1):47-52.DOI:10.13443/j.cjors.2015020702

GUO W L, LI X, LI J N, et al. The positioning accuracy analysis of multi-transmit multi-receive detection radar[J]. Chinese journal of radio science,2016,31(1):47-52. (in Chinese). DOI:10.13443/j.cjors.2015020702

资助项目: 中国电子科技集团公司技术创新基金(JJ-QN-2013-28)； 国家自然科学基金(61302006)

联系人： 郭文玲 E-mail:wenling_869@126.com