低信噪比下相位编码信号载频估计新方法

王晓峰　田润澜　张国毅

(1.海军航空工程学院电子信息工程系,烟台 264001;

2.空军航空大学信息对抗系,长春 130022)



低信噪比下相位编码信号载频估计新方法

王晓峰1,2田润澜2张国毅2

(1.海军航空工程学院电子信息工程系,烟台 264001;

2.空军航空大学信息对抗系,长春 130022)

摘要研究了电子侦察中相位编码信号的载频估计问题,提出一种低信噪比下载频估计新方法．该方法首先将相位编码信号划分为等长度的交叠区间,并计算各个区间内信号频谱的聚集性测度,然后采用网格密度聚类算法对聚集性测度进行分类,以聚类结果作为载频估计的特征类,最后叠加特征类频谱并提取峰值得出信号载频估计值．实验结果表明,该方法无需先验知识,对编码形式不敏感,且能够在较低信噪比下完成相位编码信号的载频估计,适合于电子侦察场合．

关键词电子侦察;相位编码;载频估计;低信噪比

DOI10.13443/j.cjors.2015030101

A novel carrier frequency estimation method of phase shift keying signals in low SNR

WANG Xiaofeng1,2TIAN Runlan2ZHANG Guoyi2

(1.DepartmentofElectronicEngineering,NavalAeronauticalandAstronauticalUniversity,Yantai264001,China;2.DepartmentofElectronicCountermeasure,AviationUniversityofAirForce,Changchun130022,China)

Abstract Carrier frequency blind estimation of phase shift keying(PSK) signals in the electronic reconnaissance is discussed and a novel blind estimation method in low signal to noise ratio (SNR) is proposed. The PSK signal is divided into some overlapping intervals of equal length. The spectral concentration measures of the signal in every interval are calculated based on the Fast Fourier Transform. Then, the grid-density clustering algorithm is adopted to process the spectral concentration measures, and the clustering result is regarded as the characteristic class. Finally, the spectrums of the characteristic class are accumulated to estimate the carrier frequency of the PSK signal. Experimental results shows that the proposed method, which can effectively estimate the carrier frequency in low SNR without any prior knowledge and is not sensitive to the coded type, is suitable for electronic reconnaissance occasions.

Keywords electronic reconnaissance; phase shift keying; carrier frequency estimation; low SNR

引言

相位编码信号广泛应用于现代通信和雷达领域[1-2],实现相位编码信号的正确解调,必须预先估计出信号载频．电子侦察中一般采用宽带接收机以保证较大的截获概率[3-4],而宽带接收机会导致截获信号中含有大量带外噪声,即截获信号为低信噪比(Signal to Noise Ratio, SNR)信号,并且电子侦察中没有截获信号的任何先验知识．因此,如何在无先验知识且信噪比较低的情况下准确估计相位编码信号载频是电子侦察领域的一个关键问题．

针对相位编码信号的载频估计问题,前人提出了很多方法．A J Veterbi和A M Veterbi[5]提出了相位编码信号载频盲估计的前馈最大似然估计算法(V&V算法)．以V&V算法为基础的盲最小二乘频偏估计算法[6]在通信中获得广泛应用．Mounir Ghogho, Ananthmm Swami, Tariq Durrani[7]给出了一种非线性频率估计方法(MAT算法),该方法首先计算相位编码信号的M次方去除调制信息得到正弦波信号,然后估计该正弦波信号频率后除以M获得相位编码信号载频估计值．文献[8-9]提出了应用于相位编码信号盲处理的改进MAT算法,但这些载频估计方法[5-9]均是通过非线性运算去除调制信息再进行参数估计,因此在低信噪比条件下性能不佳．文献[10]提出基于现代谱估计的相位编码信号中心频率估计算法,但这种方法计算复杂度很高,且受噪声影响严重．文献[11]提出了一种基于循环谱检测的载频估计方法,但需要相当的计算量和样本长度．文献[12]提出了一种结合功率谱频域平滑粗估计和最小二乘细估计的载频估计算法,文献[13]提出了一种基于核密度估计和均值移位的载频盲估计算法,但这两种方法的应用前提均是准确提取信号相位,而低信噪比和相位模糊均会导致信号相位难以准确提取．文献[14]提出了一种基于功率谱离散余弦变换(Discrete Cosine Transform, DCT)的二相编码(Binary Phase Shift Keying, BPSK)信号参数估值方法,但该方法仅适用于BPSK信号．

文中提出一种相位编码信号载频估计新方法．该方法首先将信号划分为等长度的交叠区间,并计算各个区间内信号的频谱,此时含有相位跳变区间的频谱为宽带频谱,不含相位跳变区间的频谱为窄带频谱;然后计算各个区间内信号频谱的聚集性测度,以聚集性测度作为特征参数进行网格密度聚类,将聚类结果作为载频估计特征类;最后将特征类对应区间的频谱进行叠加并提取峰值作为相位编码信号载频估计值．该方法无需任何先验知识,且避免了对噪声敏感的非线性运算,适合于电子侦察环境．仿真实验结果验证了估计方法的有效性．

1基本模型

相位编码信号的解析表达式可以表示为

s(n)=Aexp[j(2πf0nTs+φn+θ0)],

n=1,2,…,N,

(1)

(2)

(3)

式(1)～(3)中: A为信号幅度; f0为载频; Ts为采样间隔; tb为码元宽度; ∏为持续时间tb的门函数; Nc为编码个数; M为相位调制的阶数; θ0为信号初始相位．

电子侦察中一般采用宽带接收机,因此截获信号中会混入较强的带外噪声

r(n)=s(n)+w(n)．

(4)

式中,w(n)为复高斯白噪声,实部和虚部的方差均为0.5σ2．

相位编码信号的频谱具有一定带宽,最大谱线位置对应的频率一般不等于载频,即相位编码信号为载波抑制信号,因此要直接利用频谱估计载频,必须首先去除调制信息．去除调制信息的一般方法是对信号进行M次方运算使之转换为正弦波,然后估计正弦波频率得出相位编码信号载频估计值,但M次方过程是非线性运算,信噪比损失很大,不适用于信噪比较低的电子侦察场合．

2载频估计方法

2.1算法原理

为有效去除相位编码信号的调制信息,现给出由一阶相位差分表示的信号瞬时频率特征,图1(a)为BPSK信号瞬时频率曲线,图1(b)为载频相同的正弦波信号瞬时频率曲线．

由图1可知,相位编码信号瞬时频率相比正弦波瞬时频率仅是多了数个冲击,而这些冲击是由相位编码信号码元之间的相位跳变引起的,即码元之间的相位跳变是相位编码信号和正弦波的本质区别．相位跳变也是相位编码信号载频估计的主要障碍,如果能够去除相位跳变的影响,即去除图1(a)中相位编码信号瞬时频率的冲击之后,相位编码信号的载频估计问题就可以转化为正弦波频率估计．为此,将相位编码信号划分为等长度且相互交叠的区间,图2为区间划分示意图．

(a) 相位编码信号

(b) 正弦波信号图1　不同信号瞬时频率曲线

图2　区间划分示意图

当区间内信号不包含相位跳变时,区间内信号为正弦波,其频域表现为一个窄带频谱,图2中第一个区间内信号频谱如图3(a)所示;当区间内信号包含相位跳变时,区间内信号为相位调制信号,其频谱表现为一个宽带频谱,图2中第三个区间内信号频谱如图3(b)所示．因此,经过区间划分后的信号频谱可分为两类:窄带频谱和宽带频谱,并且窄带频谱的峰值即为相位编码信号的载频值．

(a) 不含相位跳变区间信号频谱

(b) 包含相位跳变区间信号频谱图3　区间信号频谱特性

2.2窄带频谱提取与估计

为有效区分窄带频谱和宽带频谱特征,引入时频分析中的聚集性测度衡量区间内信号频谱的宽窄带性质．聚集性测度能够有效衡量信号在变换域的能量聚集性,当信号在变换域表现为单一峰值谱线时,例如理想的正弦波频谱,聚集性测度近似为1;而信号在变换域的能量越分散,聚集性测度的值越小．因此频谱的聚集性测度可以作为区分窄带频谱和宽带频谱的特征参数．

频谱的聚集性测度定义为

(5)

(6)

窄带频谱的聚集性测度较大(接近1),而宽带频谱的聚集性测度较小,因此聚集性测度能够很好地识别出各个区间内的信号是否包含相位跳变．图4为信噪比为0dB,载频为10MHz,采样频率为50MHz,码元宽度为1μs的31位m序列的聚集性测度分布图．图中‘*’表示窄带频谱的聚集性测度,‘□’表示宽带频谱的聚集性测度．

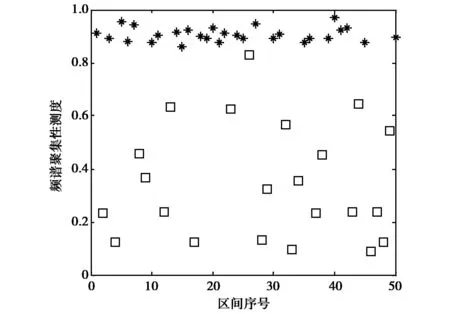
图4　聚集性测度分布

由于实际电子侦察中很难定量给出判定频谱聚集性测度的门限,因此在计算出各个区间的频谱聚集性测度后,需要一种能够自适应提取窄带频谱聚集性测度的方法．数据挖掘中的网格密度聚类算法可以在无任何先验知识的条件下,充分利用数据集自身的密度连通性完成聚类,且聚类结果与数据输入顺序无关,处理时间独立与数据对象,具有优越的实时性．因此文中将其作为提取窄带频谱聚集性测度的方法．

网格密度聚类算法的基本思想是:给定一个d维的数据集合,其属性都是有界的,将d维数据空间的每一维划分为K等份,即把数据空间分割成Kd个网格单元．网格单元相邻定义为具有共同边界或共同顶点的两个网格．若一个网格单元密度大于给定的阈值ε,则认为其是密集网格,否则视为非密集网格,非密集网格中的点视为奇异数据点．聚类就是相邻密集网格连通的最大集合．

窄带频谱和宽带频谱的聚集性测度分布特征符合网格密度聚类的要求,窄带频谱聚集性测度的分布范围较小,即窄带频谱的聚集性测度将形成密集网格;而宽带频谱是由相位跳变引起的,其数值具有随机性,因此其聚集性测度分布范围较大,即宽带频谱的聚集性测度将形成非密集网格．将各个区间频谱的聚集性测度作为一维参数输入到网格密度聚类中,输出的聚类结果即为窄带频谱,输出的奇异数据点即为宽带频谱．将所有的窄带频谱叠加后提取峰值位置即为相位编码的信号载频估计值．

2.3区间长度设置

区间划分的目的是区分窄带频谱和宽带频谱,因此区间长度不能超过信号的码元宽度,而区间长度过小会导致区间内的信号采样点数过少,使得区间内信号频谱的聚集性测度受噪声影响严重．大量仿真实验表明,区间划分长度为2tb/3时载频估计性能较佳．

在非协作条件下,信号的码元宽度是一个未知参量,因此需要预先对其进行粗略估计,已知相位编码信号的码元宽度等于信号带宽的倒数,即

tb=1/B．

(7)

因此可以通过估计信号带宽得出码元宽度的粗估计值,根据此粗估计值设置合理的区间划分长度．

综合考虑带宽的估计精度和抗噪性,采用文献[15]给出的基于功率谱全序列平滑的相位编码信号带宽估计方法,首先计算信号的频谱,然后对功率谱进行平滑:

(8)

式中: Y(m)为信号的频谱; L为平滑宽度．

设Ys(k)的最大幅值为Ys(k0),搜索Ys(k)中大于0.5Ys(k0)的所有谱线,这些谱线所占的宽度即为信号的3dB带宽,即

(9)

式中: k1和k2分别为大于0.5Ys(k0)的谱线中第一根和最后一根对应的离散频点; fs为信号采样频率．

2.4算法步骤及性能分析

相位编码信号载频估计的步骤如下:

1) 计算信号的快速傅里叶变换,并按式(8)对频谱进行平滑,得到Ys(k);

2) 搜索Ys(k)中大于0.5Ys(k0)的所有谱线,按式(9)计算码元宽度估计值;

3) 根据码元宽度估计值,设置区间划分长度对信号进行交叠划分;

4) 计算各个区间内信号的频谱和频谱的聚集性测度;

5) 对各个区间的频谱聚集性测度进行网格密度聚类;

6) 将聚类结果对应区间的频谱叠加后提取峰值作为相位编码信号载频的估计值．

信号的采样频率是影响载频估计性能的主要因素．这是由于信号码元宽度一定,区间划分长度也一定,而区间内信号频谱特性的好坏完全取决于区间内信号的采样点数,即取决于采样频率．当信号采样频率较高时,区间内信号的采样点数较多,此时区间内信号频谱的抗噪性较好,频谱的聚集性测度相对准确;当信号采样频率较低时,区间内信号的采样点数较少,此时区间内信号频谱的抗噪性较差,频谱的聚集性测度误差较大,而各个区间内信号频谱的聚集性测度准确与否直接影响相位编码信号载频估计的准确性．关于信号采样频率对载频估计性能的具体影响将会在仿真实验部分进行具体分析．

3仿真分析

利用雷达和通信中常用的BPSK信号和四相编码(Quadrature Phase Shift Keying, QPSK)信号对文中提出的载频估计方法进行Matlab仿真验证,共设计了两组仿真实验．实验一主要考察信号采样频率对载频估计性能的影响,进而定量地给出各采样频率下算法的适用信噪比;实验二与文献[12]提出的最小二乘拟合估计(Least Squares Fitting Estimation, LSFE)方法进行比较,验证本文方法的载频估计性能．仿真中信号的载频为10 MHz,码元宽度为1 μs,BPSK为31位m序列,QPSK为64位Frank码,每个信噪比进行1 000次蒙特卡洛仿真实验,并计算载频估计的均方误差(Mean Square Error, MSE)．

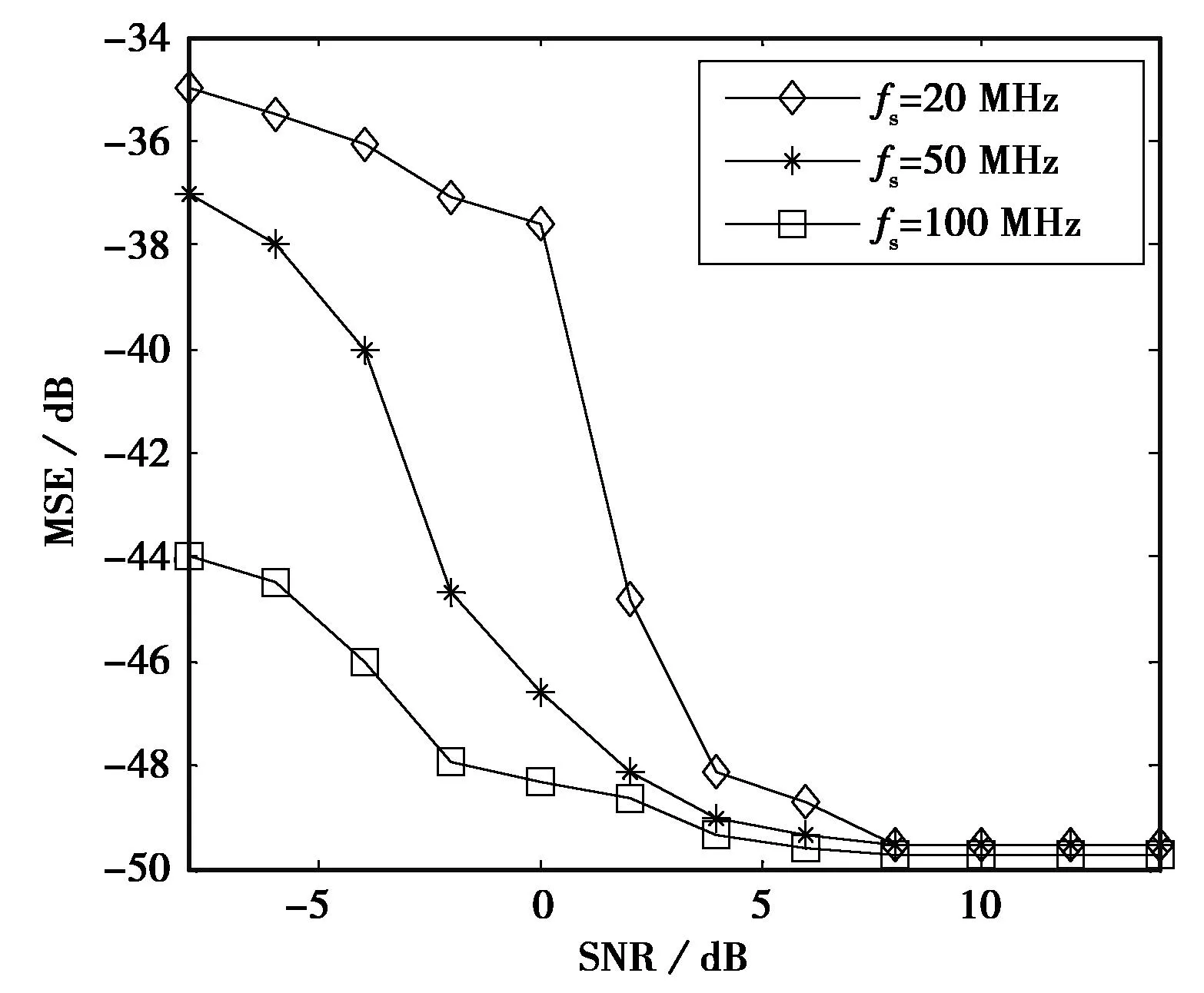
实验一本实验主要考察信号采样频率对载频估计性能的影响,图5为BPSK和QPSK信号在采样频率分别为20、50和100 MHz时的载频估计均方误差曲线．

实验结果表明:当信号采样频率较高时,算法载频估计的信噪比门限较低,如采样频率为100 MHz时,算法的信噪比门限约为-2 dB;而当信号采样频率较低时,算法的信噪比门限较高,如采样频率为20 MHz时,算法的信噪比门限约为4 dB．对比图5(a)和图5(b)可知,BPSK和QPSK信号的载频估计性能几乎相同,这是由于该方法无需提取具体的相位跳变值,因此对相位跳变值不同的BPSK和QPSK信号具有相同的估计性能,即该方法对相位编码信号的编码形式不敏感．

实验二本实验将本文方法与LSFE方法进行参数估计性能对比．BPSK和QPSK信号的采样频率均为50 MHz,两种方法的载频估计均方误差曲线如图6所示．

(a) BPSK载频估计性能

(b) QPSK载频估计性能图5　不同采样频率下载频估计性能曲线

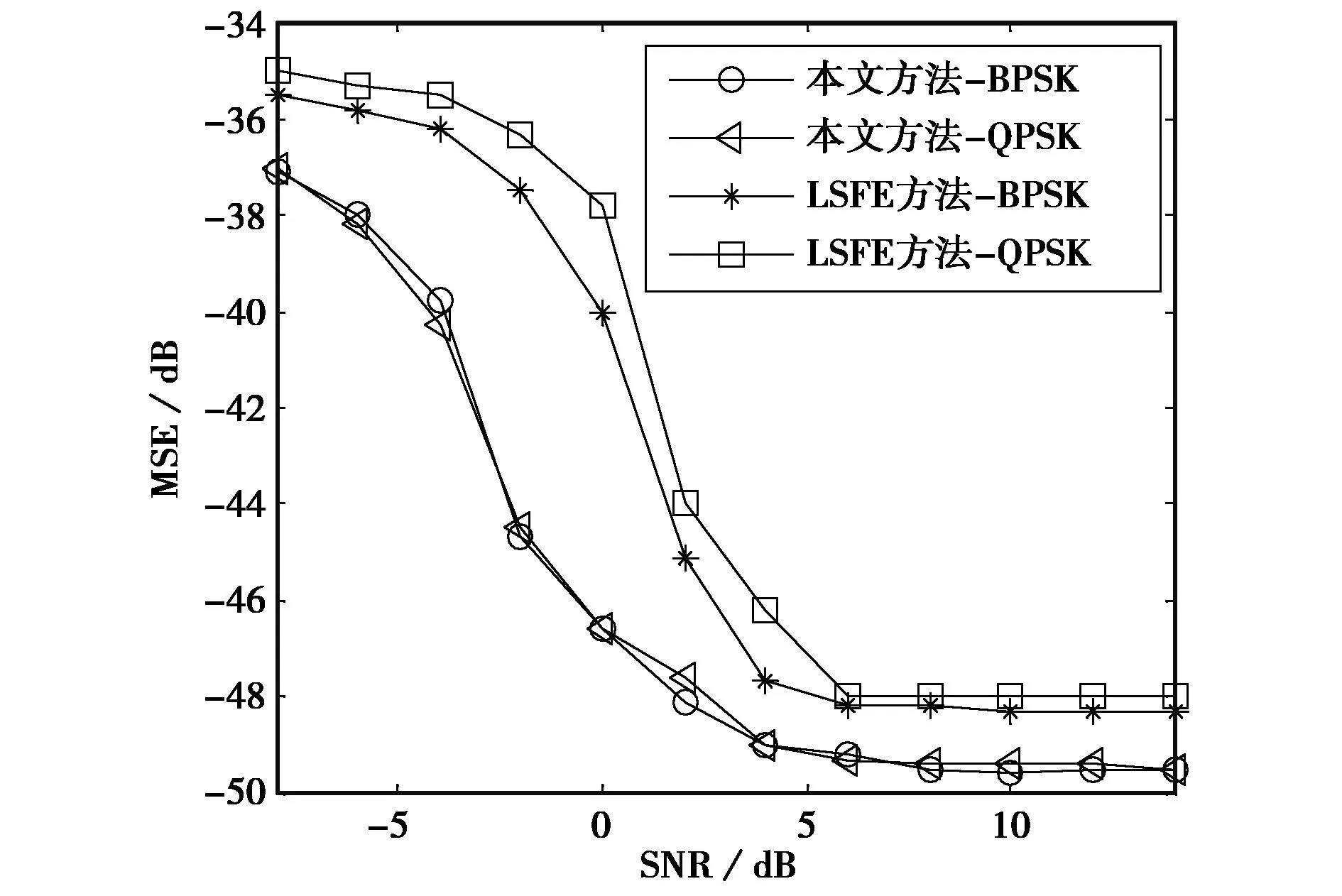
图6　载频估计性能对比

实验结果表明:在不同的噪声强度下,本文方法对BPSK和QPSK信号载频估计均性能优于LSFE方法．这是因为LSFE方法需要直接提取信号相位并准确判定相位跳变值,这些都极易受到噪声的影响,且由于BPSK信号的相位跳变值大于QPSK信号,因此该方法对BPSK信号的载频估计性能优于QPSK信号;而本文方法直接对信号进行区间划分,利用信号频谱的聚集性判定区间内是否包含相位跳变,在去除相位跳变对载频估计影响的同时,很好地抑制了噪声,因此能够在较低信噪比下完成相位编码信号的载频估计,且对编码形式不敏感,适合于先验知识未知的电子侦察场合．

4结论

本文根据相位编码信号的瞬时频率特征,提出了一种低信噪比下相位编码信号载频估计新方法,该方法无需对信号进行非线性运算,也无需直接提取信号相位,显著降低了相位编码信号载频估计的信噪比门限．仿真实验表明,该方法可以在较低的信噪比环境下完成相位编码信号的载频估计,且无需任何先验知识,对编码形式不敏感,适合应用于电子侦察环境．该方法同样适用于协作通信中相位编码信号的频偏估计,如何提高载频估计在低采样频率时的抗噪性是下一步需要研究的问题．

参考文献

[1]曾祥能, 张永顺, 何峰, 等. 相位编码信号的综合旁瓣能量改善技术[J]. 电波科学学报, 2012, 27(1): 172-176.

ZENG X N, ZHANG Y S, HE F, et al. The integrated sidelobe level phase coded improved technology for waveform[J]. Chinese journal of radio science, 2012, 27(1): 172-176.(in Chinese)

[2] 冯志红, 赖涛, 赵拥军. 低信噪比下对称三角线性调频信号参数估计[J]. 电波科学学报, 2012, 27(3): 520-525.

FENG Z H, LAI T, ZHAO Y J. Parameter estimation of STLFMCW signals in low SNR[J]. Chinese journal of radio science, 2012, 27(3): 520-525. (in Chinese)

[3] 戴幻尧, 刘勇, 李永帧, 等. 一种新的天线空域极化特性的远场测量方法[J]. 应用科学学报, 2009, 27(6): 606-611.

DAI H Y, LIU Y, LI Y Z, et al. Far field measurement for spatial polarization characteristics of antenna[J]. Journal of applied sciences, 2009, 27(6): 606-611. (in Chinese)

[4] VETERBI A J, VETERBI A M. Nonlinear estimation of PSK-modulated carrier phase with application to burst digital transmissions[J]. IEEE transactions on infomation theory, 1983,29(4): 543-551.

[5] 王红星, 王洪利, 毛忠阳, 等. 基于循环谱特性的扩展二元相移键控解调算法[J]. 电波科学学报, 2010, 25(5): 934-939.

WANG H X, WANG H L, MAO Z Y, et al. Demodulation algorithm for EBPSK based on cyclic spectrum characteristic[J]. Chinese journal of radio science, 2010, 25(5): 934-939. (in Chinese)

[6] ZHU D M, MATHEWS V J, DETIENNE D H. A phase likelihood-based algorithm for blind identification of PSK signals[C]//IEEE International conference on acoustics, speech and signal processing. florence, May 4-9, 2014: 5730-5734.

[7] GHOGHO M, SWAMI A, DURRANI T. Blind estimation of frequency offset in the presence of unknown multipath[C]//IEEE International Conference on Personal Wireless Communications. Piscataway, 2000: 104-108.

[8] 李广参, 冯永新, 钱博, 等. 基于FPGA的BPSK信号载频估计单元设计与实现[J]. 电子技术, 2014(7): 38-41.

LI G S, FENG Y X, QIAN B, et al. Design and realization of BPSK signal carrier frequency estimation unit based on FPGA[J]. Electronic technology, 2014(7): 38-41. (in Chinese)

[9] 赵艳, 罗胜恩, 万坚. 基于子带信号的MPSK载频估计算法[J]. 系统工程与电子技术, 2012, 34(3): 592-597.

ZHAO Y, LUO S E, WAN J. MPSK carrier frequency estimation algorithm based on subband signals[J]. Systems engineering and electronics, 2012, 34(3): 592-597. (in Chinese)

[10]王戈, 严俊. 一种基于功率谱估计的盲载频估计新算法[J]. 计算机工程与应用, 2012, 48(13): 44-117,129.

WANG G, YAN J.Novel algorithm for blind carrier frequency estimation based on power spectrum calculation[J].Computer engineering and applications, 2012, 48 (13): 114-117. (in Chinese)

[11]JIN Y, JI H B. A novel cyclic-moment based method for DS-SS QPSK signal blind parameter estimation[J]. Chinese journal of electronics, 2011, 20(4): 94-100.

[12]邓振淼, 刘渝. MPSK信号载频盲估计[J]. 通信学报, 2007, 28(2): 94-100.

DENG Z M, LIU Y. Blind estimation of MPSK carrier frequency[J]. Journal on communications, 28(2): 94-100.(in Chinese)

[13]李小捷, 许录平, 陈佳. 基于均值移位的载频盲估计算法[J]. 系统仿真学报, 2009, 21(5): 1451-1454+1458.

LI X J, XU L P, CHEN J. Blind estimation of carrier frequency with mean shift algorithm[J]. Journal of system simulation, 2009, 21(5): 1451-1454+1458.(in Chinese)

[14]马秀荣, 曹多. 基于功率谱离散余弦变换的BPSK信号参数估值[J]. 电子与信息学报, 2014, 36(9): 2075-2080.

MA X R, CAO D. Parameters estimation of BPSK signals based on power spectral DCT[J]. Journal of electronics & information technology, 2014, 36(9): 2075-2080. (in Chinese)

[15]DANDREA A N, MENGALI U, REGGIANNINI R. The modified Cramer-Rao bound and its application to synchronization problems[J]. IEEE transactions on communications, 1994, 42(2/4): 1391-1399.

王晓峰(1987-),男,河北人,海军航空工程学院电子信息工程系博士研究生,研究方向为信号与信息处理、电子对抗.

田润澜(1973-),女,河北人,博士,空军航空大学副教授、硕士生导师,研究方向为航空电子侦察情报分析、雷达侦察极化信息处理.

张国毅(1965-),男,吉林人,博士,空军航空大学教授、博士生导师,研究方向为航空电子侦察情报分析、电子对抗.

作者简介

中图分类号TN911.7

文献标志码A

文章编号1005-0388(2016)01-0091-07

收稿日期：2015-03-01

王晓峰, 田润澜, 张国毅. 低信噪比下相位编码信号载频估计新方法[J]. 电波科学学报,2016,31(1):91-97. DOI: 10.13443/j.cjors.2015030101

WANG X F, TIAN R L, ZHANG G Y. A novel carrier frequency estimation method of phase shift keying signals in low SNR [J]. Chinese journal of radio science,2016,31(1):91-97. (in Chinese). DOI: 10.13443/j.cjors.2015030101

资助项目: 国家自然科学基金重点项目(61301237)； “十一五”总装备部武器装备预研项目(51309060308)

联系人： 王晓峰 E-mail: wxf870516@126.com