稀布同心圆环阵列的半径优化方法
陈客松 朱永芸 倪霄龙
(电子科技大学电子工程学院,成都 611731)
稀布同心圆环阵列的半径优化方法
陈客松朱永芸倪霄龙
(电子科技大学电子工程学院,成都 611731)
摘要针对有阵列孔径阵元总数和最小阵元间距约束的稀布同心圆环阵列综合问题,提出了一种基于修正遗传算法(Modified real Genetic Algorithm, MGA)的半径优化方法.通过约束同一圆环上阵元间距相等,利用MGA优化圆环的半径,获得最小的峰值旁瓣电平.该方法不仅降低了优化的计算量和模型的复杂性,而且还有效地改善了阵列的旁瓣性能.仿真结果证明了该方法的有效性和鲁棒性.
关键词稀布同心圆环阵列;修正遗传算法;旁瓣性能
DOI10.13443/j.cjors.2015040302
Optimum method of grid ring radii of sparse concentric rings array
CHEN KesongZHU YongyunNI Xiaolong
(SchoolofElectronicEngineering,UniversityofElectronicscienceandTechnologyofChina,Chengdu611731,China)
Abstract An optimization method of grid ring radii based on modified genetic algorithm is presented under the constraints of fixing the aperture, the number of elements and the minimum element spacing. We make element spacing on the same ring equal, and make use of modified genetic algorithms(MGA) to optimize grid radii to minimize peak sidelobe level. The proposed method can improve performance of sidelobe level(SLL) of the sparse concentric ring arrays and can meanwhile relatively reduce computational cost. Finally, the simulation results confirm the great efficiency and robustness.
Keywords sparse concentric rings array; modified genetic algorithms(MGA); sidelobe level(SLL)
引言
一般情况下,由单个辐射器构成的天线就可以完成发射和接收电磁波的任务.但在一些特殊应用中,往往要求天线具有强大的方向性和很高的增益,有时还要求天线波瓣可以扫描,并具有一定的形状等,这时就需要使用多个辐射器,并按一定方式排列.如果各个天线单元排列成一个圆环,就称之为圆阵.圆阵不仅可以提供360°的方位角,而且可以通过循环移动阵列激励,简单而灵活地操纵波束的方位,在俯仰方向上也有一个理想的方向特性.同时,圆结构的对称性使其波束形状和天线增益等性能基本维持平衡,并大体上保持互耦平衡[1].
由于圆阵所具有的这些优势,使其正得到日益广泛的应用,但是圆阵方向图却具有相对主瓣较高的旁瓣电平.在给定阵列孔径阵元总数和最小阵元间距等约束条件的前提下,如何优化设计阵元的分布位置来最大限度地降低阵列的峰值旁瓣电平(Peak Side-Lobe Level, PSLL),综合出尽量低的旁瓣电平是阵列天线研究的重要课题之一[2-4].
近60年来,均匀间隔阵列的综合已获得了广泛而深入的研究,在保持原始阵列的辐射特性下减少阵元数的研究已有很多方法,例如给定阵元数和阵列响应,可以利用传统的道尔夫切比雪夫综合法、泰勒综合法、傅里叶逆变换法和数值优化等方法实现阵列综合;相对而言,非均匀阵列的综合是尚未解决的难题.阵元间约束条件下的优化有两种途径:一种是阵元从相距半波长的规则栅格上稀疏的稀疏阵[5];另一种是天线单元在设计时约束其阵元间距在一定孔径范围内随机稀布的稀布阵[6].近年来,为了得到峰值旁瓣性能良好的稀疏阵,已经出现了统计优化法、动态规划法、遗传算法[7-9]、模拟退火法[10]、粒子群法[11]等综合算法.
过去同心圆环阵列旁瓣性能优化研究的对象,大多是阵元只能在各圆环等间距栅格上稀疏分布[11-12].文献[13]中首先固定稀疏同心圆环阵列各圆环上的阵元位置和数目,然后分别运用遗传算法和粒子群算法优化阵元的激励幅度和相位来降低阵列的PSLL.文献[14]运用经典的遗传算法先优化各个圆环上的阵元数目,再优化阵元的分布位置,从而实现旁瓣性能最优的稀疏同心圆环阵列.然而针对拥有更大的自由度和更好的旁瓣性能的稀布同心圆环阵列,国内外却鲜有研究.
文中提出一种基于修正遗传算法(Modified real Genetic Algorithm, MGA)的圆半径优化的方法,约束同一圆环的阵元间距,利用MGA优化稀布同心圆阵列的半径,降低了优化的计算量和模型的复杂性,又对所有阵元进行了联合优化,在优化圆环半径的同时,也确定了各个圆环上的阵元数目.
1稀布同心圆环阵列模型
当不同半径的圆环阵列具有相同的圆心,且天线单元在设计时约束其阵元间距在一定孔径范围内随机稀布时,构成了同心圆环阵列[15],如图1所示.

图1 同心圆环阵列模型
同心圆环阵列的方向图函数[14]为
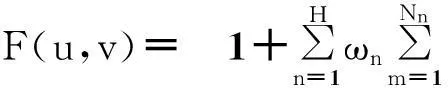
sin(φm)v)].
(1)
式中: Nn为第n个圆环上的阵元数; H为圆环的个数; k=2π/λ; λ为波长; ωn为第n个圆环上的激励; rn为第n个圆环的半径; (rncos(φm)u,rnsin(φm)v)为阵元的位置; u=sinθcosφ; v=sinθsinφ; φm=2π(m-1)/Nn.同心圆环阵列天线单元在布阵时约束其在一定孔径范围内随机分布,其环间距互不相等,构成了稀布同心圆环阵列.当圆心处固定一个阵元,则稀布同心圆环阵列的方向图函数可表示为

rnsin(φi)v)].
(2)
式中,N为圆环上阵元的总数.
当优化设计的稀布同心圆环阵列共有H个圆环,各圆环的半径为r0,r1,r2,…,rH时,且优化变量为圆环的半径,优化设计目标是要获得可视区PSLL最低的稀布同心圆环阵列.则优化模型可以表示为
(3)
式中:
(4)
Fmax是主瓣峰值,u和v的取值区间为除主瓣区域以外的所有区域; dn为第n个圆环上的阵元间距; dc是约束的最小阵元间距.
2基于MGA的半径优化方法
在经典遗传算法中[16],通常采用二进制码“0”和“1”来编码优化变量,这种编码方式非常适合交叉和变异操作,但是其运行性能较差,且存在二进制与十进制之间的转换问题.实数编码的遗传算法以变量的真实十进制编码代表变量的编码方式,在克服二进制编码缺点的同时,还具有更好的变异多样性,从而提高了遗传算法的效率和精度.文献[17]提出了一种间接描述优化变量的修正实数遗传算法来进行稀布阵列天线的优化设计.该算法避免了优化变量(圆环半径)的直接描述,并利用阵元间距这一约束减小了遗传算法的搜索空间.下面给出基于MGA的稀布同心圆环阵列半径优化方法的主要步骤.
2.1创立初始种群
在种群中,将优化变量Ri=[r0,r1,…,rH]作为个体,因为阵元间距需大于等于dc,所以圆环半径需满足:
(5)
(6)
式中:a=L/2-Hdc,且a≥1,L是约束的圆阵孔径.文献[18]已验证当圆环由内到外,圆环半径的间距由小到大,所得的峰值旁瓣性能相对较好.由公式(6)可知,函数Δ(n)是一个递增函数,随着n的增大,Δ(n)值也增大,则圆环半径间距也增大,因此所得的旁瓣电平性能较好.由此阵元总数和圆环个数的关系满足
(7)
每个圆环上至少有一个阵元,最多等于公式(5)中最大半径的圆环有最小阵元间距时的阵元数.因为阵元数必须为整数,阵元间距必须大于最小阵元间距dc,所以向下取整.在满足公式(5)的条件下随机产生S个rn,由这样的S组[r0,r1,r2,…,rH]组成S个个体Ri,形成了初始种群R.
2.2交叉和变异
MGA的交叉和变异操作只需在修正种群中进行.进行MGA操作后的种群称为修正种群.假如选定修正种群中第i个和第j个个体的第n号基因,且满足
(8)
则可进行交叉操作,交叉作用后的两个新的个体为
Ri=sort[0,R1i,R2i,…,Rnj,…,RHi],
Rj=sort[0,R1j,R2j,…,Rni,…,RHj].
(9)
假如选定第l个个体的第z个基因进行变异,则变异作用后的新的个体为

R(z+1)l,…,RHl].
(10)
式中:随机数ξ⊆(0,0.5L),且dc≤|ξ-Ril|,0≤i≤H且i≠z.发生交叉和变异的基因数由事先给定的交叉率和变异率决定.
2.3选择
经过交叉和变异操作得到的种群为

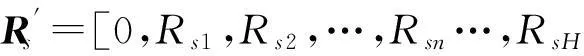
(11)
已知半径(种群个体)和dn,则Nn可表示为
(12)
因为阵元的数目必须是整数,所以公式(12)中的值在2πRsn/dn周围.为了使得dn≥dc,使阵元间距足够大,所以向下取整.
根据φm=2π(m-1)/Nn,φm能够被计算出来,因此能够得阵元的位置为(rncos(φm)u,rnsin (φm)v).
将阵元位置与圆环半径代入公式(2)得阵列因子,再将所得阵列因子代入公式(4)求得稀布同心圆环阵列的PSLL.然后采用截断选择法,并根据截断阀值选择个体,选择较低PSLL的个体,并用较低PSLL的个体取代较高的PSLL的个体,由此产生新种群.新种群再依次进行交叉、变异和选择,进行迭代,直到达到最大遗传代数,迭代结束,得到最优个体.
3仿真实例
为了说明基于MGA的稀布同心阵元半径方法的有效性,文中给出以下两个实例优化PSLL,并将仿真结果与文献[14]进行了对比分析.设定阵元均为理想的全向天线单元,各阵元等幅同相激励,且阵列主波束指向阵列中心法线方向.MGA的基本参数为:种群数100;采用截断选择法且截断阀值为0.5;交叉概率0.2;变异概率0.02;终止代数为200.
例1优化阵元总数为201的稀布同心圆环阵列
根据文献[14],设置阵元总数N=201,孔径L=9.96λ,最小阵元间距dc=0.5λ.根据公式(6)可得圆环个数H<8,又根据公式(7)可得圆环个数H>5,所以圆环个数H=6或7.当H=6时,各个圆环半径取公式(5)中最大值,阵元间距取最小值时,阵元总数为212,所以当H=6时,阵元总数为201时,几乎为满阵,优化圆环半径毫无意义.所以此时取H=7.图2为单次实验收敛曲线和5次实验平均收敛曲线图.图3为最优的稀布圆阵的阵列方向图.图4为最优的阵元分布图.表1显示了本文的最优结果并与文献[14]进行比较.在相同的目标和相同的阵元总数的条件下,半径优化方法所得的PSLL为25.45dB,相比运用混合遗传算法(HybridGeneticAlgorithm,HGA)优化的PSLL降低了2.51dB.仿真结果证明了半径优化方法具有较好的效率和鲁棒性.

图2 收敛曲线图(N=201)

图3 最优的阵列方向图(N=201)
例2优化阵元总数为142的稀布同心圆环阵列
根据文献[14],设置阵元总数N=142,孔径L=9.4λ,最小的阵元间距dc=0.5λ.根据公式(6)得圆环个数H<8,又根据公式(7)得圆环个数H>4,所以圆环个数H=5,6或7.当H=7,阵元间距过大,产生栅瓣电平;当H=5时,各个圆环半径取公式(5)中的最大值,阵元间距取最小值时,总阵元数为166.所以当H=5,阵元总数N=142时,几乎为满阵,优化半径毫无意义.因此这里取圆环个数H=6.图5为单次实验收敛曲线和5次实验平均收敛曲线图.图6为最优的阵列方向图.图7为最优的阵元分布图.表2显示了本文的最优结果并与文献[14]进行比较.在相同的目标、相同的阵元数和相同的圆环个数的条件下,半径优化方法所得的PSLL为28.07dB,相比运用HGA优化的PSLL降低了0.25dB.
文中的所有仿真均在MATLABR2010中完成,计算机配置为:Intel(R)Core(TM)i5-4570处理器,主频为3.2GHz.从表中可以看出,基于MGA的半径优化方法,与经典遗传算法相比,能在阵元数确定的情况下,同时优化圆环半径和圆环上阵元数目,实现了更好的旁瓣性能.实验结果验证了文中优化方法的有效性和鲁棒性.

表1 例1优化结果比较

表2 例2优化结果比较

图4 最优的阵列分布图(N=201)

图5 收敛曲线图(N=142)

图6 最优的阵元方向图(N=142)

图7 最优的阵元分布图(N=142)
4结论
文中提出一种基于修正遗传算法的半径优化方法.与文献[12]比较,此方法虽然是遗传迭代技术,但是能在优化设计过程中同时处理圆环孔径,阵元总数和最小阵元间距的约束问题.因此,更加适用于某些特殊情况.该方法为解决该类阵列优化问题提供了有益的启示,所得优化结果也为实际工程运用提供了有价值的参考.此外,为了得到较好的旁瓣电平,文中首次给出了圆环半径间距递增的函数,可以拓展运用到其他形式的圆阵优化设计当中.
参考文献
[1]SINGHU,KAMALTS.Synthesisofthinnedplanarconcentriccircularantennaarraysusingbiogeography-basedoptimisation[J].IETmicrowaves,antennas&propagation, 2012, 6(7): 822-829.
[2]KUMARBP,BRANNERGR.Generalizedanalyticaltechniqueforthesynthesisofunequallyspacedarrayswithlinear,planar,cylindricalorsphericalgeometry[J].IEEEtransactionsonantennasandpropagation, 2005, 53(2): 621-634.
[3]ZHANGWJ,LIL,LIF.Reducingthenumberofelementsinlinearandplanarantennaarrayswithsparsenessconstrainedoptimization[J].IEEEtransactionsonantennasandpropagation, 2011, 59(8): 3106-3111.
[4]唐斌, 郑美燕, 陈客松, 等. 运用增广矩阵束方法稀布优化平面阵[J].电波科学学报, 2013, 28(3): 540-546.
TANGB,ZHENGMY,CHENKS.Sparseantennaarraysynthesisusingmatrixenhancementandmatrixpencil[J].Chinesejournalofradioscience, 2013, 28(3):540-546. (inChinese)
[5]RAJO-IGLESIASE,QUEVEDO-TERUELO.Thinnedarraysynthesisincludingradiationpatterndiversityintheelements[C]//ProceedingsoftheIEEEElectromagneticsinAdvancedApplications(ICEAA).Torino,September12-16,2011.IEEE, 2011: 853-856.DOI: 10.1109/ICEAA. 2011.6046455.
[6]LISW.Gratelobes/sidelobessuppressionforsparsearraydesignbyusinggeneticalgorithms[C]//ProceedingsoftheIEEEInnovationsinBio-inspiredComputingandApplications(IBICA),Shenzhen,DecemberIEEE, 2011: 371-373.DOI: 10.1109/IBICA. 2011.97.16-18,2011.
[7] 陈客松, 何子述.平面稀布阵列的优化算法[J].电波科学学报, 2009, 24(2): 193-198.
CHENKS,HEZS.Synthesisapproachforsparseplanearrays[J].Chinesejournalofradioscience, 2009, 24(2):193-198. (inChinese)
[8]HAUPTRL.Thinnedarraysusinggeneticalgorith-ms[J].IEEEtransactionsonantennasandpropagation, 1994, 42(7): 993-999.
[9]MANDALD,MAJUMDARA,KARR,etal.Thi-nnedconcentriccirculararrayantennassynthesisusinggeneticalgorithm[C]//IEEEStudentconferenceonresearchanddevelopment,Putrajaya,December19-20,2011.IEEE,2011: 194-198.DOI: 10.1109/SCOReD.2011,6148734.
[10]郭陈江, 张锋, 丁君, 等. 基于循环差集与模拟退火法的阵列综合[J]. 电波科学学报, 2007, 22(6): 962-964.
GUOCJ,ZHANGF,DINGJ,etal.Arraysynthesisusingcyclicdifferencesetsandsimulatedannealing[J].Chinesejournalofradioscience, 2007, 22(6): 962-964. (inChinese)
[11]MANDALD,KARR,GHOSHALSP.Thinnedconcentriccirculararrayantennasynthesisusingparticleswarmoptimizationwithconstrictionfactorandinertiaweightapproach[C]//InternationalConferenceonRecentTrendsinInformationSystems.Kolkata,December21-23.IEEE, 2011: 77-81.DOI: 10.1109/ReTIS.2011.6146844
[12]GHOSHP,DASS.Synthesisofthinnedplanarco-ncentriccircularantennaarrays—adifferentialevolutionaryapproach[J].JournaloftheprogressinelectromagneticsresearchB, 2011, 29: 63-82.
[13]REYNAA,PANDUROMA.Designofsteerableconcentricringsarrayusingrotationpropertiesandevolutionaryoptimization[C]//ProceedingsoftheIEEEAntennasandPropagation(EuCAP).Barcelona,April12-16,2010.IEEE,2010: 1-5.
[14]HAUPTRL.Optimizedelementspacingforlowsidelobeconcentricringarray[J].IEEEtransactionsonantennasandpropagation, 2008, 56(1): 266-268.
[15]SUNXJ,GANQ,TANGB.Designofsparseconcentricmulti-circulararrayusingmicro-geneticoptimumalgorithm[C]//ProceedingsoftheIEEECommunicationsandMobileComputing,Yunnan,January6-8,2009.IEEE, 2009: 51-55.DOI:10.1109/CMC.2009.121.
[16]WHITLEYD.Ageneticalgorithmtutorial[J].Jou-rnaloftheStatisticsandComputing, 1994, 4(2):65-85.
[17]CHENKS,HEZS,HANCL.AmodifiedrealGAforthesparselineararraysynthesiswithmultipleconstraints[J].IEEEtransactionsonantennasandpropagation, 2006, 54(7): 2169-2173.
[18]DASR.Concentricringarray[J].IEEEtransactionsonantennaspropag, 1966, 14(3):398-400.

陈客松(1973-),男,四川人,电子科技大学电子工程学院副教授,硕士生导师,研究方向为阵列天线、相控阵雷达及信号处理.

朱永芸(1991-),女,湖南人,电子科技大学电子工程学院硕士,研究方向为稀布阵列及信号处理.

倪霄龙(1989-),男,山东人,电子科技大学电子工程学院硕士,研究方向为数字图像处理机及矩阵处理.
作者简介
中图分类号TN820.1+5
文献标志码A
文章编号1005-0388(2016)01-0110-06
收稿日期:2015-04-03
陈客松, 朱永芸, 倪霄龙. 稀布同心圆环阵列的半径优化方法[J]. 电波科学学报,2016,31(1):110-115. DOI: 10.13443/j.cjors.2015040302
CHEN K S, ZHU Y Y, NI X L. Optimum method of grid ring radii of sparse concentric rings array [J]. Chinese journal of radio science,2016,31(1):110-115. (in Chinese). DOI: 10.13443/j.cjors.2015040302
资助项目: 国家自然科学基金(U1233103)
联系人: 朱永芸 E-mail:zhuyongy1991@sina.cn

