系梁对连续刚构桥抗震性能的影响

张洁，曾金明

(1.武昌工学院土木工程学院，湖北武汉　430065；2.中交第二公路勘察设计研究院有限公司，湖北武汉　430056)



系梁对连续刚构桥抗震性能的影响

张洁1，曾金明2

(1.武昌工学院土木工程学院，湖北武汉430065；2.中交第二公路勘察设计研究院有限公司，湖北武汉430056)

摘要：为研究系梁对桥墩地震响应的影响，以连续刚构桥为研究对象，基于Perform-3D有限元软件，分别建立无系梁和设置系梁的计算模型，对2种计算模型进行动力特性分析、非线性时程分析。分析结果表明：设置系梁可以提高桥梁整体受力能力，减小桥梁的自振周期，改变桥梁的自振振型；设置系梁可以明显增大系梁处桥墩的地震响应，而对其他部分的墩身影响不明显；随着地震加速度的增大，系梁对桥墩地震响应的影响有增大的趋势。

关键词：系梁；非线性分析；地震响应

随着墩高的增加，为了满足桥墩整体抗弯刚度的要求，同时为了改善桥墩抵抗顺桥向的水平力作用，常常在桥墩中增加横向联系[1]。目前在双薄壁墩间设置系梁对桥墩地震响应影响的研究较少。文献[2]建立线弹性模型分析系梁道数、系梁刚度和系梁位置对结构自振特性的影响，并分析系梁对桥梁地震响应影响；文献[3]基于OpenSees软件，对无系梁和系梁桥墩模型进行时程反应分析和弹塑性分析；文献[4]以系梁设置位置、系梁与桥墩截面刚度比以及系梁模拟方式为基本参数，分析结构的动力特性及地震响应的变化；文献[5]对跨径为30 m双柱式高墩连续梁桥进行模态分析和反应谱分析，讨论横系梁的数量、不同布置方式以及不同截面尺寸对桥墩内力的影响；文献[6]以设置2道横系梁的双柱墩曲线梁桥为背景，考虑曲线梁桥的弯扭耦合效应和主梁间的非均匀碰撞效应，研究不同位置横系梁和横系梁刚度对桥梁地震反应的影响；文献[7]以一座典型双肢薄壁刚构桥为工程背景，采用增量动力分析方法，考虑行波效应，分析系梁道数、系梁刚度等参数对桥梁远场地震响应的影响。由以上研究可以发现，系梁对桥梁地震影响的研究较少，并且多采用线弹性模型进行分析。本文以连续刚构桥为研究对象，基于Perform-3D[8]建立计算模型，分析讨论系梁的设置对桥墩结构非线性[9-10]地震响应的影响。

1工程实例及计算模型建立

1.1单元模型

本文以一连续刚构桥为研究对象，该桥主桥跨径布置为(95+180+95) m，桥面宽度为12.25 m，主梁采用变高度预应力混凝土单箱单室箱梁，箱梁根部高度11.0 m，跨中高度4.0 m，箱梁根部底板厚1.2 m，跨中底板厚0.32 m，箱梁高度以及箱梁底板厚度按1.8次抛物线变化。主桥桥墩采用双肢矩形空心墩，肢间净距7.0 m；桥墩沿顺桥宽度为3.5 m，沿横桥宽度为9.0 m，壁厚均为0.9 m，肢间净距7.0 m；墩高为80 m。

在混凝土桥墩中，合理定义桥墩的恢复力模型[11]对准确模拟桥墩的非线性行为很关键。目前结构的非线性分析单元主要有塑性铰单元[12-13]和纤维单元。为了较准确地模拟出桥墩的非线性行为，桥墩采用纤维模型，即选取建立在材料应力-应变关系层次上的恢复力曲线模型。桥墩的纤维划分见图1。

为了分析增设系梁对桥梁地震响应的影响，建立两种计算模型。模型1为不考虑双薄壁墩中的系梁，模型2在桥墩中部处设置系梁，有限元模型如图2所示。

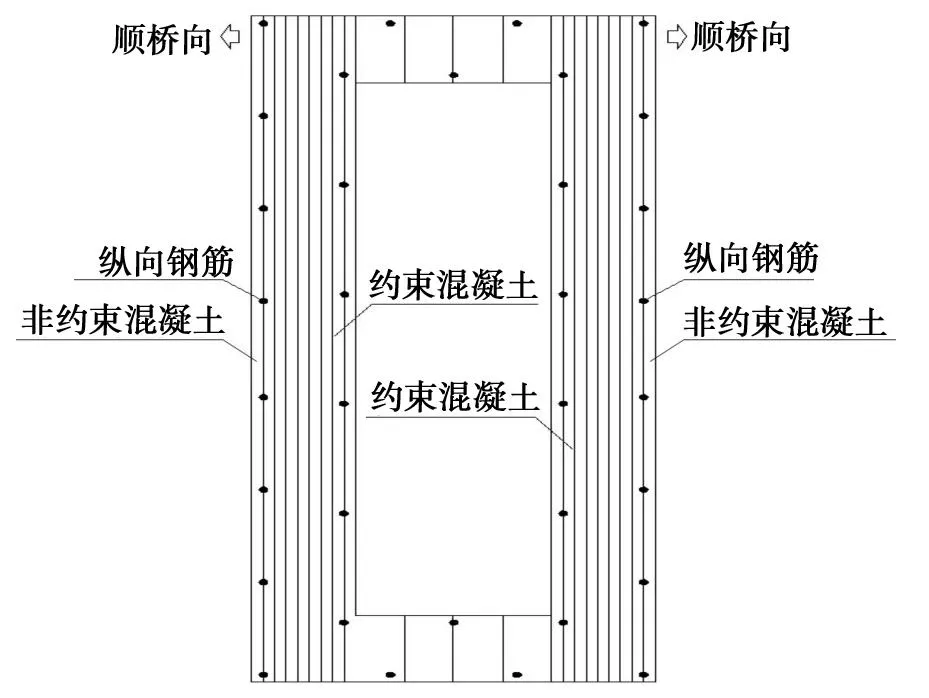
图1　桥墩纤维划分

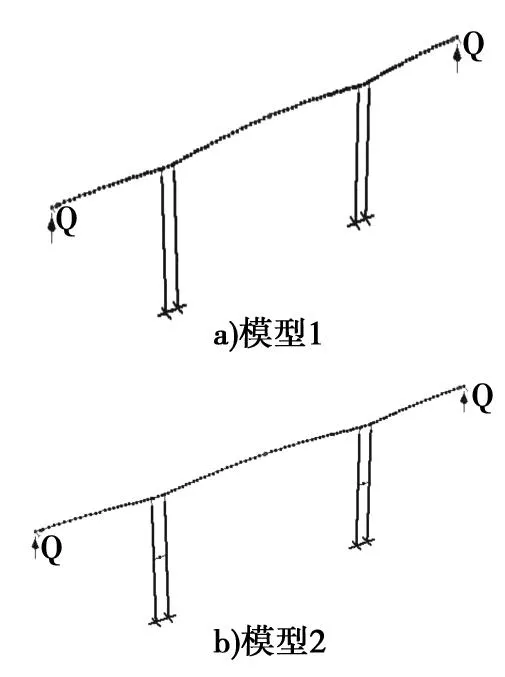
图2　有限元模型

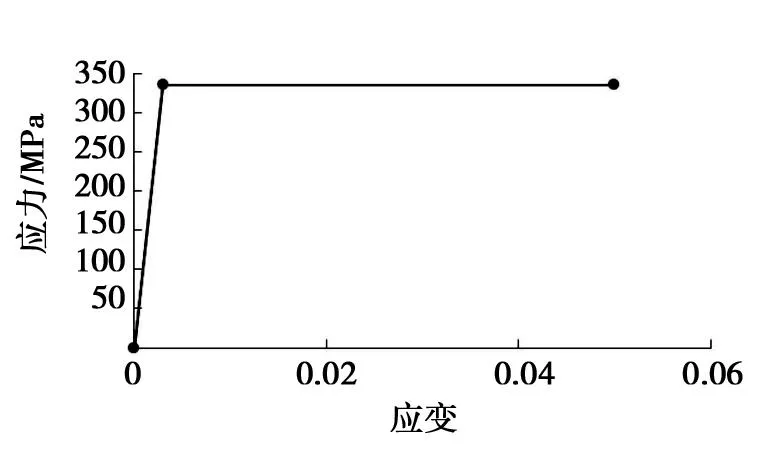
图3　钢筋应力-应变关系

1.2应力应变曲线

1.2.1钢筋本构模型

各国学者都曾对钢筋混凝土的本构关系进行了研究，并提出了多种计算模型，如Ramberg-Osgood本构关系[14]、Richard本构模型[15]、Giuffre-Menegotto-Pinto等修正滞回变形的钢筋本构模型[16]。桥墩主筋采用HRB335钢筋。钢筋采用理想弹塑性模型，其本构关系见图3。

1.2.2混凝土本构模型

本文混凝土采用Mander模型[17]，该模型的本构关系见图4。

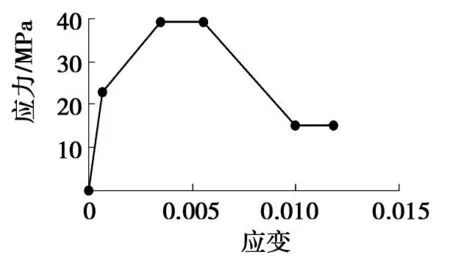
图4　混凝土的应力-应变曲线

2动力特性分析

对上述两种模型进行动力特性分析，其前10阶频率及振型特点如表1所示。

由表1可知：1)相比模型1，模型2结构的自振周期均有减小，这是因为增设系梁后增大了桥梁结构的整体刚度；振型为横向弯曲时，自振周期减小不明显，振型为顺桥向弯曲时，自振周期减小较明显，以第2阶顺桥向弯曲振型为例，相比模型1，模型2的振动周期减小了38%；2)在结构的前10阶频率中，模型2的振型与模型1的振型在第6阶和第7阶不同。图5列出了模型1的前5阶振型。

3非线性地震响应分析

1)地震波选择

本文选择了有代表性的3条地震波，3条波地震动记录如表2所示。

2)非线性地震响应分析

根据桥梁所处的地震场地类型，设计水平加速度为0.3g(g为重力加速度)，为了分析结构的非线性地震响应，将加速度峰值调为0.51g。表3为加速度为0.51g时3条地震波作用下的桥墩响应。

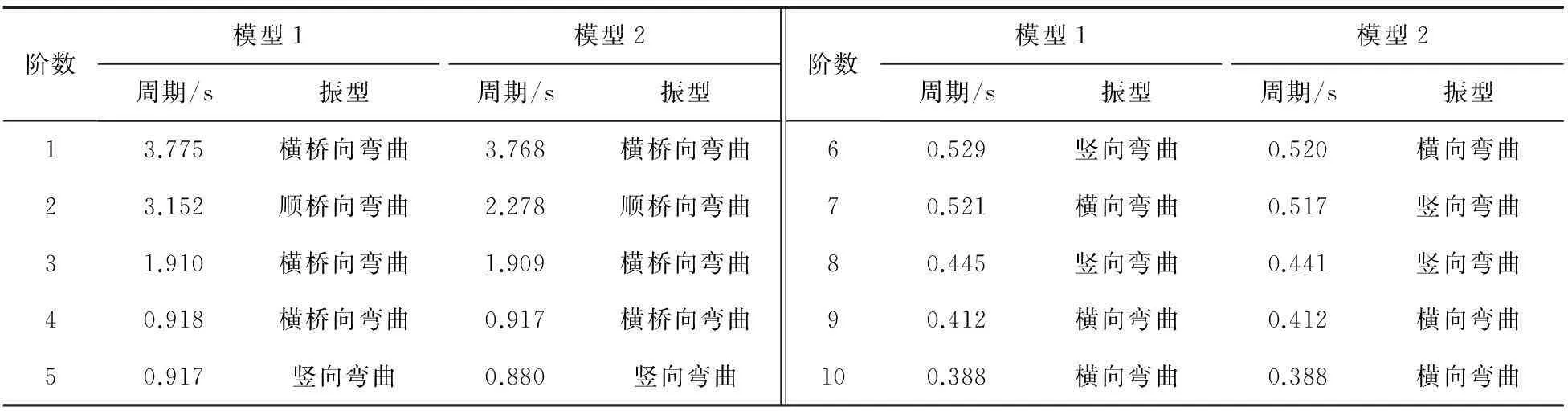
表1　桥梁前10阶频率

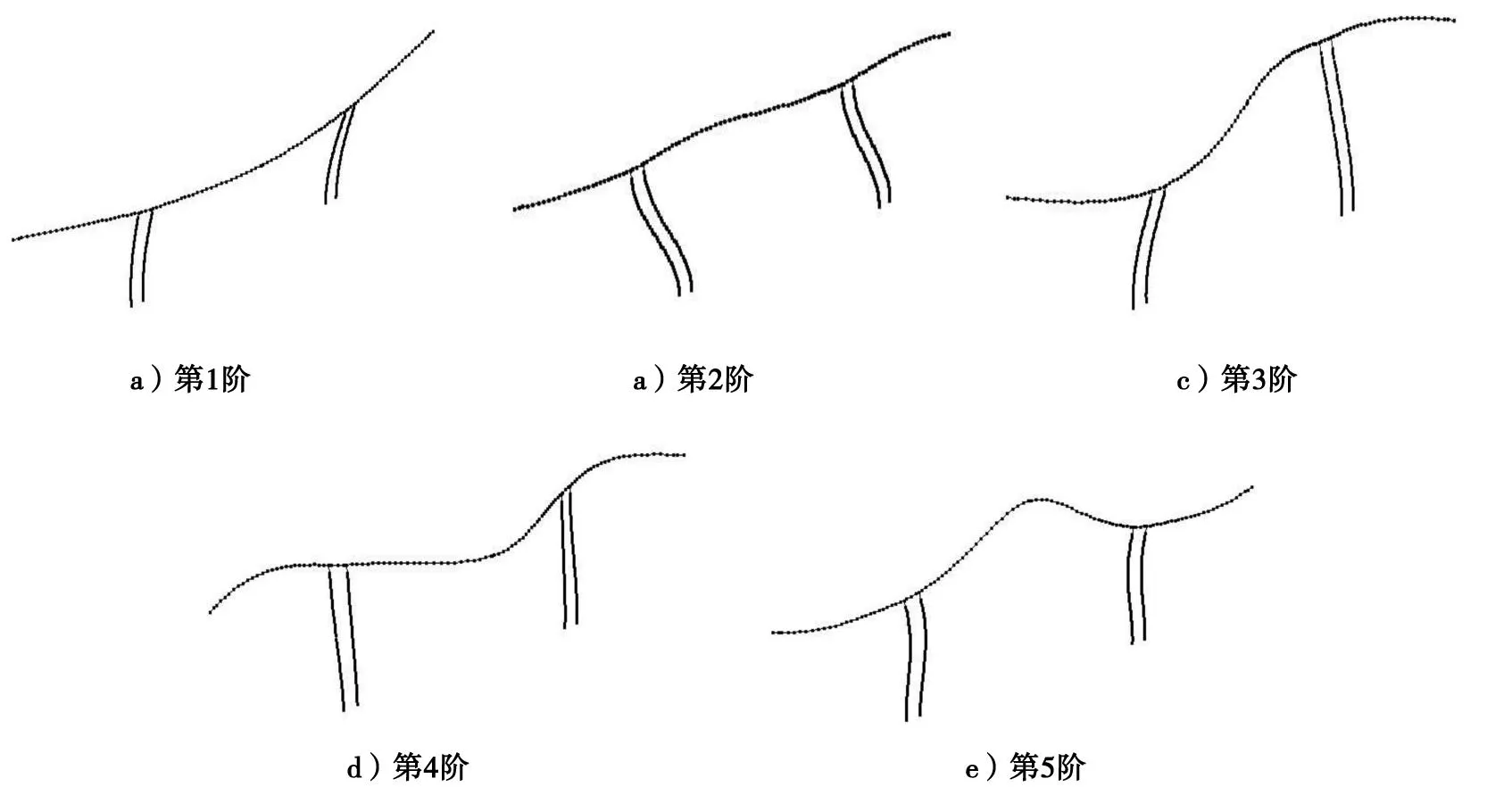
图5　模型1前5阶振型

由表3可知，相比模型1，模型2在W1地震波作用下的墩顶位移增加了24%，墩底弯矩增加64%，墩底曲率增加了88%；在W2地震波作用下，模型2墩顶位移增加了7%， 墩底弯矩增加51%， 墩底曲率增加了160%；在W3地震波作用下，模型2墩顶位移减小20%，墩底弯矩增加了10%，墩底曲率增加了10%。由上述可知，设置系梁增大了桥墩墩底的地震响应，改变了墩顶位移。

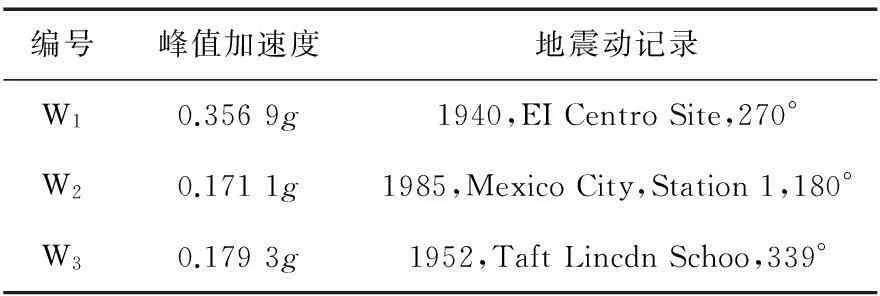
表2　地震动记录表

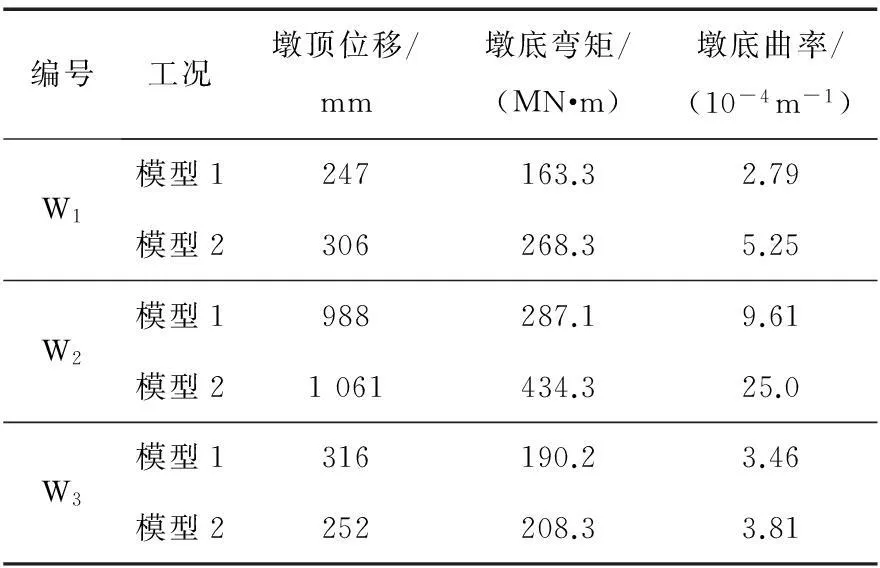
表3　地震波作用下桥墩响应

图6为3条地震波作用下墩身曲率沿着墩身的变化曲线。由图6可知，在地震作用下，模型1桥墩顶部和底部都将产生较大的曲率，而在桥梁中部，曲率较小；模型2在系梁设置处墩身曲率较大，甚至超过墩顶曲率。例如：在W1地震波作用下，系梁设置处墩身曲率为-3.61×10-4m-1，与模型1相比，模型2增大了866%，与墩顶曲率3.69×10-4m-1相差不大；在W2地震波作用下，系梁设置处墩身曲率为-1.64×10-3m-1，与模型1相比，模型2增大了4 857%，超过墩顶曲率1.45×10-3m-1；在W3地震波作用下，系梁设置处墩身曲率为-2.9×10-4m-1，与模型1相比，模型2增大了863%，与墩顶曲率2.99×10-4m-1相差不大。

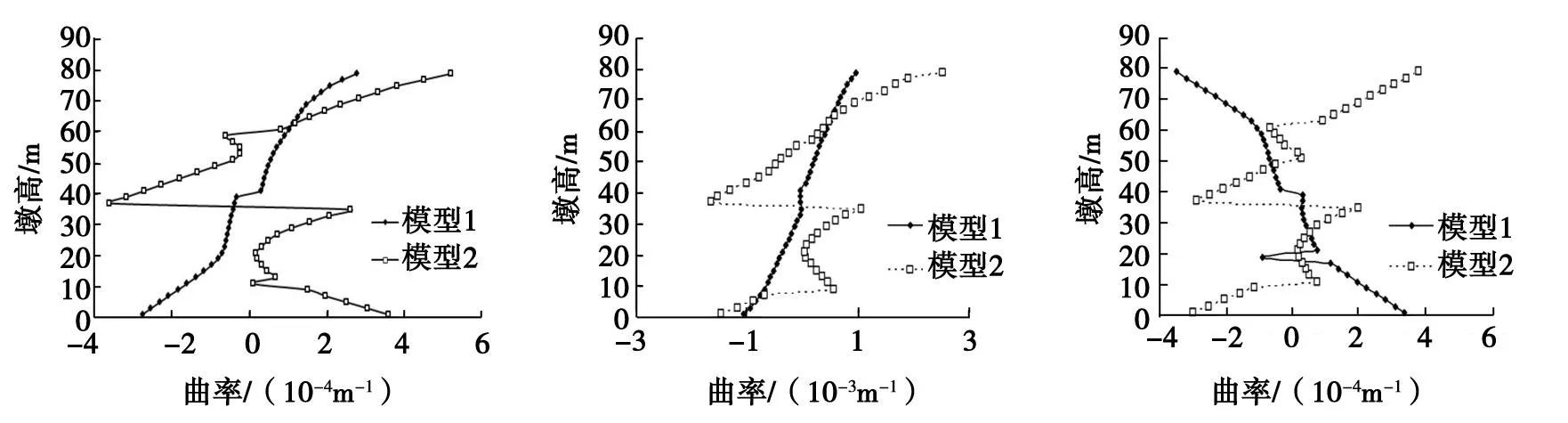
a)W1　　　　　　　　　　　　　　b)W2　　　　　　　　　　　　　c) W3图6　地震波作用下墩身曲率曲线

图7为3条地震波作用下墩身弯矩的变化曲线。由图7可知，系梁对墩身弯矩的影响与系梁对墩身曲率影响有相同的规律。由上述分析可知，增设系梁后，系梁设置处的墩身曲率、墩身弯矩明显增大，甚至超过墩顶曲率和墩顶弯矩。

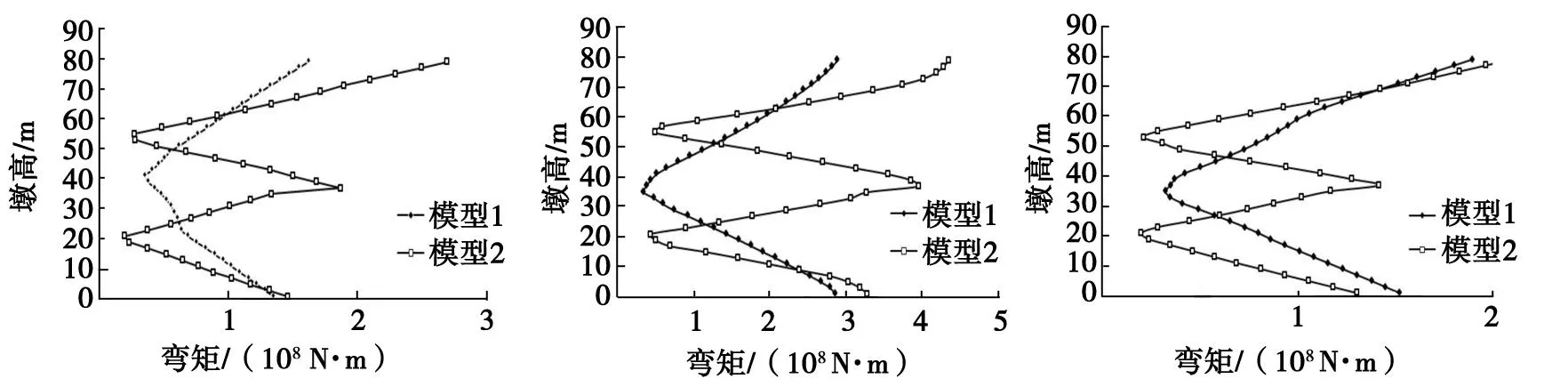
a)W1　　　　　　　　　　　　　b)W2　　　　　　　　　　　　c) W3图7　地震波作用下墩身弯矩曲线

图8为在3种地震波作用下两种计算模型墩底滞回曲率曲线。由图8可以看出，模型2的墩底屈服明显大于模型1，这说明系梁的增设增加了桥墩墩底的地震响应，对抗震是不利的。

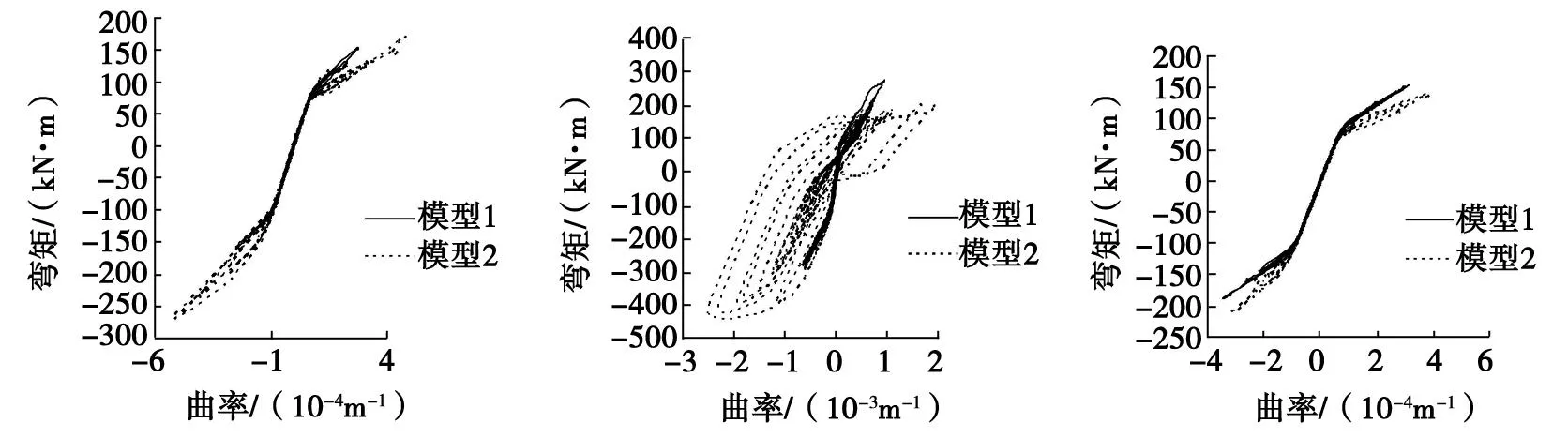
a)W1　　　　　　　　　　　　b)W2　　　　　　　　　　　　c) W3图8　墩底滞回曲线

4IDA分析

1)地震波选取

本文为了分析结果更具代表性，选择不同场地条件下的7条地震波，7条波地震动记录如表4所示。

2)IDA分析

为了进一步分析系梁对桥梁非线性地震响应的影响，现选择7条地震波分别对模型1和模型2进行逐步增量时程分析(Incremental Dynamic Analysis,IDA)。

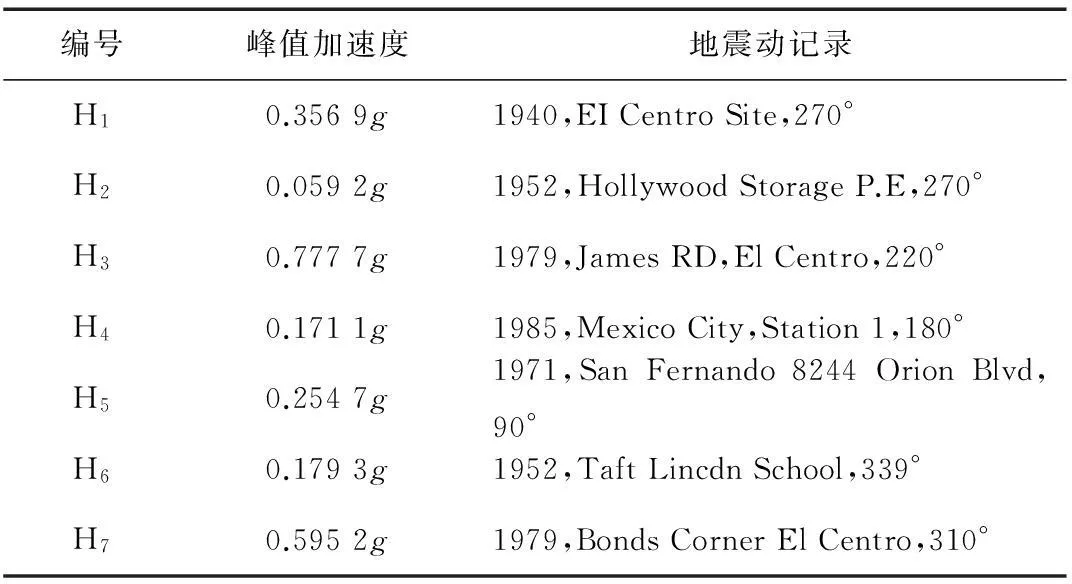
表4　地震波记录

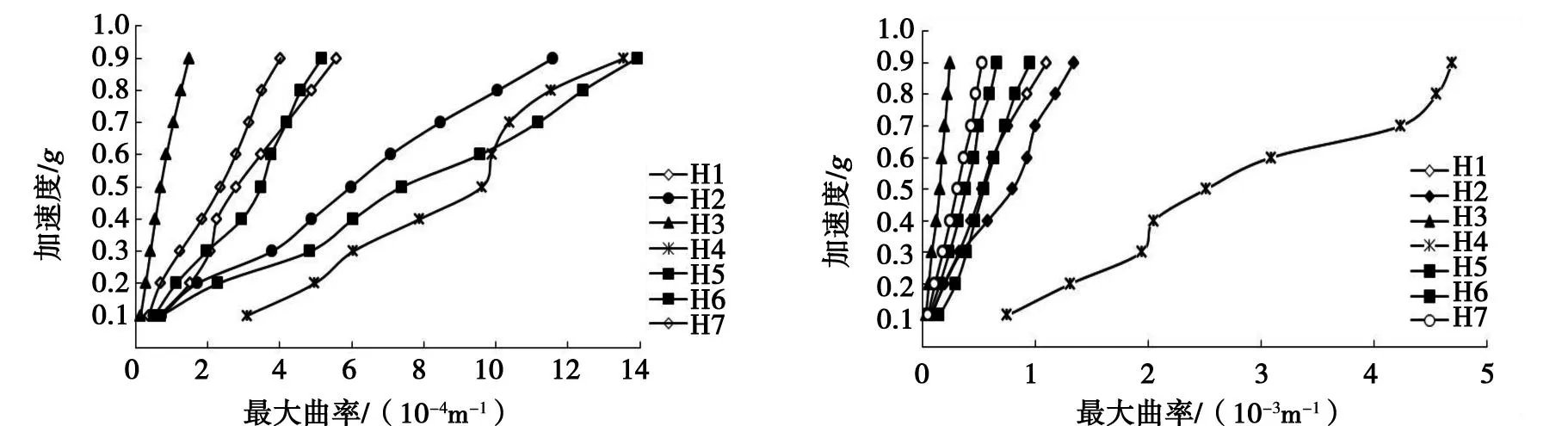
图9为2种计算模型的墩底最大曲率与加速度关系曲线。

由图9可知：桥墩墩底的最大曲率随着地震波峰值的增加而增大；对比模型1，除了H5地震波外，在其他6条地震波作用下，增设系梁都增大了墩底最大曲率，最大增大率达到308%。

由于7条地震波计算结果基本类似，现仅列出H1地震波作用下墩顶位移、墩底弯矩和墩底曲率于表5。图10为桥墩墩顶位移、墩底弯矩和曲率随加速度峰值的变化曲线。

a) 模型1　　　　　　　　　　　　　　　　　　　　　b) 模型2图9　墩底最大曲率与加速度的关系曲线

加速度墩底弯矩/(MN·m)墩底曲率/(10-5m-1)墩顶位移/cm模型1模型2模型1模型2模型1模型20.1g75.087.56.67.67.56.80.2g109.5158.015.218.615.213.90.3g127.9205.220.530.620.720.80.4g147.9240.322.643.323.526.30.5g163.3268.327.952.524.730.60.6g174.2290.734.861.628.536.80.7g191.6305.842.075.435.045.10.8g212.1329.548.892.142.152.60.9g229.6345.455.7109.049.360.11.0g250.4354.362.7127.056.667.5

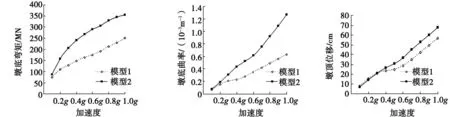
由图10和表5可知：在地震波作用下，随着加速度峰值的增加，墩顶位移、墩底弯矩和墩底最大曲率也随着增加；当加速度峰值小于0.2g时，两种计算模型的计算结果相差不大，当加速度峰值超过0.2g时，模型2的墩顶位移、墩底弯矩和墩底最大曲率明显大于模型1。

当加速度为0.6g时，模型2墩底弯矩相比模型1增大了67%；当加速度为1.0g时,墩底曲率增大了102%；当加速度为0.6g时,墩顶位移增大了29%，进一步说明增设系梁可以较大的增加桥墩非线性地震响应。

a) 墩底弯矩　　　　　　　　　　　　　b) 墩底曲率　　　　　　　　　　　c) 墩顶位移图10　桥墩响应值随加速度变化曲线

5结论

本文以一双薄壁连续刚构桥梁为分析对象，采用纤维模型模拟桥墩单元，分别对无系梁和设置系梁2种计算模型进行动力特性分析、非线性分析，分析系梁对桥墩地震响应的影响，得出以下主要结论：1)增设系梁增大了桥梁结构的整体刚度，减小了桥梁的振动周期，改变了结构的振型；增设系梁对顺桥方向振动影响明显，以第2阶顺桥弯曲为例，增设系梁后振动周期减小了38%。2)增设系梁增大了桥墩墩底内力和曲率，改变了墩顶位移，以EI Centro 地震波作用下为例，增设系梁后墩顶位移增加了24%，墩底弯矩增加64%，墩底曲率增加了88%；增设系梁对系梁设置处的墩身弯矩和曲率影响明显，而对墩身其他部分的弯矩和曲率影响较小，以EI Centro 地震波作用下为例，系梁设置处墩身弯矩为186.91 MN·m，相比不设置系梁增大了332%，超过墩顶弯矩145 950 MN·m。3)随着加速度的增大，墩身弯矩和曲率也在增大，系梁对墩身弯矩和曲率的影响也有增大的趋势；在加速度峰值为0.2g，相比不设置系梁，设置系梁后的墩底弯矩增大了44.3%；墩底曲率增大了22.4%；而在加速度峰值为0.6g时，相比不设置系梁，设置系梁后的墩底弯矩增大了66.9%，墩底曲率增大了77.0%。

参考文献：

[1]马宝林.高墩大跨连续刚构桥[M].北京:人民交通出版社，2001.

[2]周勇军,赵煜，贺拴海.系梁设置对高墩大跨弯连续刚构桥动力特性及地震响应的影响[J].应用基础与工程学科学报,2011,19(4):608-617.

ZHOU Yongjun, ZHAO Yu, HE Shuanhai.Effect of tie beam on the dynamic behavior and seismic response of curved rigid frame bridge with high piers and long span[J].Journal of Basic Science and Engineering, 2011,19(4):608-617.

[3]尚维波，张春宁.高墩刚构桥系梁抗震分析[J].长安大学学报(自然科学版),2012,32(1):62-65.

SHANG Weibo, ZHANG Chunning. Seismic analysis of tie beam of rigid frame bridge with high pier[J].Journal of Chang′ an University(Natural Science Edition), 2012,32(1):62-65.

[4]商宇，叶爱君，翁健健. 横系梁对双柱墩及其基础地震反应的影响[J].结构工程师，2013,29(5):96-100.

SHANG Yu,YE Aijun,WENG Jianjian.Effects of the link beam on seismic responses of the double-column pier and its foundation[J].Structural Engineers, 2013,29(5):96-100.

[5]兰峰，王克海.中小跨径双柱式高墩桥梁横系梁对抗震性能的影响[J].公路交通科技, 2011,28(5):92-97.

LAN Feng, WANG Kehai.Influence of collar beam of double column high-rise pier bridge with short span on seismic performance[J].Journal of Highway and Transportation Research and Development,2011,28(5):92-97.

[6]董方超，孙广俊，李鸿晶.横系梁对双柱墩混凝土曲线梁桥地震反应的影响分析[J].世界桥梁，2015,43(3):75-81.

DONG Fangchao, SUN Guangjun, LI Hongjing.Analysis of cross tie beam on seismic reaction of curved concrete bridge with two-columned piers[J].World Bridges, 2015,43(3):75-81.

[7]陈彦江，郝朝伟，李勇.系梁设置对双肢薄壁刚构桥地震响应影响分析[J].自然灾害学报，2015,24(4)：63-70.

CHEN Yanjiang, HAO Chaowei, LI Yong. Effect of tie beam on seismic response of rigid frame bridge with double-leg thin-walled piers[J].Journal of Natural Disasters, 2015,24(4)：63-70.

[8]Computers and Structures Inc.Getting started of perform-3D[M].Version 4. California: Computers and Structures Inc,2006.

[9]VAMVATSIKOS D, CORNELL C A. Incremental dynamic analysis [J].Earthquake Engineering and Structural Dynamics, 2002,31(3):491-514.

[10]谢肖礼，王波，张伟峰，等.罕遇地震作用下高墩连续刚构桥双重非线性抗震分析[J].工程力学，2009，26(4):113-115.

XIE Xiaoli, WANG Bo, ZHANG Weifeng, et al. Double nonlinear aseismic analysis of high-rise pier and rigid frame bridges under rear earthquake[J].Engineering Mechanics, 2009，26(4):113-115.

[11]陆新征.建筑抗震弹塑性分析—原理、模型与在ABAQUS，MSC.MARC和SAP2000上的实践[M].北京：中国建筑工业出版社，2009.

[12]CLOUGH R W, BENUSKA K L, WILSON E L.Inelastic earthquake response of tall buildings[C]//Proceeding of the Third World Conference on Earthquake Engineering.New Zealand: New Zealand National Committee on Earthquake Engineering, 1965.

[13]GIBERSON M F. Two nonlinear beams with definitions of ductiltiy[J].Journal of the Structural Division,Proceedings of the American Society of Civil Engineerings,1969,95(2):137-157.

[14]RAMBERG W，OSGOOD W R．Description of steel strain curve by three parameters[R]．Washington D C:National Advisory Committee for Aeronantics,1943.

[15]RICHARD R M, ABBOTT B J.Versatile elastic-plastic stress-strain formula[J].Journal of the Engineering Mechanics Division,1975,101：511-515.

[16]MENEGOTTO M，PINTO P E. Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending[J].Proceeding of IABSE Symposium on Resis-tance and Ultimate Deformability of Structures Acted on by Well-Defined Repeated Loads, 1973:15-22.

[17]MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J].Journal of Structural Engineering,1988,114(8):1804-1826.

(责任编辑：刘勇波)

Influence of Collar Beam on Seismic Performance of Continuous Rigid Frame Bridge

ZHANGJie1，ZENGJinming2

(1.SchoolofCivilEngineering,WuchangInstituteofTechnology,Wuhan430065,China；2.CCCSecondHighwayConsultantsCo.，Ltd.，Wuhan430065,China)

Abstract:In order to study the effect of the collar beam on the seismic responses of the bridge pier, the continuous rigid frame bridge is taken as the research object. Based on the finite element program Perform-3D, the calculation models without the collar beam and with the collar beam are established respectively. The dynamic characteristics analysis and nonlinear analysis are made on the two calculation models. The analytical results show that the collar beam improves the overall force capacity of the bridge, reduces the natural vibration period of the bridge and changes the natural vibration of the bridge, that the collar beam significantly increases the seismic response of the bridge pier with the collar beam, without obvious impact on other parts of the piers and that with the increase of earthquake acceleration, the collar beam has more tendency to influence the seismic responses of the bridge pier.

Key words:collar beam；non-linear analysis；seismic response

中图分类号：U442.5

文献标志码：A

文章编号：1672-0032(2016)01-0040-07

DOI：10.3969/j.issn.1672-0032.2016.01.008

作者简介：张洁(1986—)，女，山东菏泽人，讲师，工学硕士，主要研究方向为桥梁抗震及防震减灾,E-mail：zj300600@163.com.

基金项目：武昌工学院校级科研立项项目(2014KYZ07)

收稿日期：2016-01-11