我国创业板市场风险的度量及分析——基于随机波动率模型的实证研究

黄秀海，　龚泳旭

(浙江财经大学 数学与统计学院， 浙江 杭州 310018)



我国创业板市场风险的度量及分析
——基于随机波动率模型的实证研究

黄秀海，龚泳旭

(浙江财经大学 数学与统计学院， 浙江 杭州 310018)

摘要：创业板自上市以来，其高风险问题一直是学术界和实务界研究的重点问题。为精确度量创业板市场风险，将MCMC参数估计方法引入到随机波动率模型中，进而计算出基于随机波动率模型的创业板市场风险价值(VaR)。实证结果显示：在一天持有期内，在95%的置信水平下，创业板市场发生的最大损失不会超过3.19%；在99%的置信水平下，创业板市场的最大损失不会超过4.45%。此外本文还使用GARCH族模型对创业板市场的风险进行了辅助研究。

关键词：创业板；MCMC参数估计方法；随机波动率模型

一、引言

2009年10月30日，28家公司在深圳交易所创业板正式挂牌上市，标志着创业板市场正式登上我国资本市场的历史舞台。创业板与大型成熟的主板市场相比，特征迥然不同。创业板市场降低了中小企业的上市门槛，其上市标准低于成熟的主板市场，而且风险高，股本规模小，业绩不突出，但也因此更加注重公司的信息披露，为具有高成长性的中小企业提供直接融资的渠道。因此，创业板的推出对缓解我国中小企业普遍融资困难的困局有着积极的作用，促进了我国多层次资本市场体系的建立。然而自创业板市场成立以来，对其的褒贬不一，普遍认为创业板存在着严重的“三高”问题，即高溢价、高市盈率、高股价，从而导致了资源浪费、二级市场风险过高。创业板市场的高风险不仅影响到投资者的投资收益，而且影响到整个股票市场乃至金融市场的稳定发展，已经成为学术界和实务界广泛关注的重点难题。

风险测量是风险管理的核心和基础，是对风险的定量分析和评估。20世纪90年代以来，VaR作为一种风险评价方法在国际上得到了广泛的应用，是目前金融市场风险衡量的主流方法。传统的VaR计量方法主要有方差协方差法、历史模拟法、蒙特卡罗模拟法等。但是传统的VaR方法在度量金融风险时存在一定的局限性，比如方差-协方差法是在假设金融资产收益率服从正态分布的基础上，对资产可能发生的最大损失进行度量，这种假设与一般金融数据尖峰厚尾的数据结构特征不相符合，本文引入基于MCMC参数估计下的随机波动率模型，将金融资产收益率的波动聚集效应对风险度量的影响考虑进模型中，并分别计算两种模型下的风险价值(VaR)，以期对创业板的市场风险进行度量。

二、文献综述

风险价值(Value at Risk,VaR)的思想最早是由Baumol(1952)提出的，随后VaR风险度量办法迅速地被全球各大金融机构所采用，成为到目前为止在理论和实践方面均获得高度认可的风险度量模型。国际上利用VaR模型衡量金融市场风险的文献很多，Philippe Jorion(1995)对比分析了正态分布和t分布下的静态模型计算的VaR的区别[1];Lee，Saltoglu(2002)选取1983年至2000年日本股票市场交易数据，构建基于方差-协方差法、历史模拟法以及蒙特卡罗模拟法的VaR模型，并将极值理论引入到对日本股票市场的风险度量中，实证结果表明极值理论下的VaR模型的有效性低于其他传统理论的VaR模型[2]。国内学者对于风险度量理论也进行了广泛而深入的研究，主要集中在对各种风险度量模型的比较分析，其中对VaR方法的模型构建和实际测算的研究比较深入。王春峰，万海辉等(2000)指出了VaR模型主流计算方法中的缺陷，提出了基于马尔科夫链蒙特卡洛模拟的VaR计算方法，研究表明基于马尔科夫链蒙特卡洛模拟的VaR模型克服了传统蒙特卡洛模拟法存在的缺陷，有效地提高了模型估计精度[3]。黄宇红(2009)认为权证收益率序列具有尖峰厚尾的特征，他们通过选取包钢权证的交易数据为研究对象，构建了EGARCH模型和TGARCH模型来计算VaR的值，实证结果表明EGARCH-VaR模型对风险的预测较为准确，TGARCH-VaR模型略微低估了风险值[4]。

从国内国外使用VaR度量金融市场风险的研究可以看出，学者们对VaR风险度量方法的研究已经非常深入，形成了许多重要的VaR的计算理论和方法。与波动率模型结合的VaR计算方法能很好的刻画金融资产收益率的波动聚集效应，成为目前应用最为广泛的风险度量方法。自创业板在深圳交易所上市以来，国内还没有学者使用VaR方法度量创业板的市场风险，而创业板板市场的高风险问题已经成为学术界、实务界和监管层关注的重点问题，本文将对这一重要问题进行研究。

三、计量模型

(一)VaR计算的基本原理

Jorion给出了VaR的一个比较权威的定义，可以简单表述为：在正常的市场条件下，在一定置信水平下，金融资产或投资组合在未来特定的一段时间内可能遭受的最大损失。根据定义，VaR可以用数学语言表示为：

P(ΔW>VaR)=1-c

其中，P()为事件发生的概率，ΔW为金融资产或组合在持有期内遭受的损失，VaR为在置信水平c下的风险价值。

(二)基于随机波动率模型的VaR模型

标准的SV模型如下：

其中yt是第t期去掉均值μ后的收益率，ht是对数波动，α、β、γ为待估参数，β为持续性参数，它反应了当前波动对未来波动的影响程度。误差过程εt与ηt互不相关，εtN(0,1)，ηtN(0,1)，ηt是随机误差项，故ht不可观测。

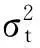
随机波动率模型具有数理金融学和金融计量经济学双重根源,被认为是刻画金融市场波动性的最理想模型。Harvey A、Kim等学者做过大量关于SV模型与GARCH模型的比较研究,认为SV模型所刻画的波动性与金融市场特征更加吻合。但是对标准SV模型进行参数估计存在较大困难，实证结果发现基于MCMC估计的SV模型参数估计效果最好。本文将采用基于Gibbs抽样的马尔科夫链模拟(MCMC)法来估计SV模型参数。

(三)VaR模型的准确性检验

VaR模型的准确性检验是指VaR模型的测量结果对实际损失的覆盖程度，一个通行的方法是Kupiec(1995)提出的失败频率检验法。设N为检验样本中损失高于VaR的次数，即失败次数，T为检验样本总数，P=1-c，c是给定的置信度。检验的假设为：

似然比检验统计量：

在原假设下，统计量LR服从自由度为1的χ2分布。它的95%的置信区间临界值为3.841，所以如果LR>3.841，我们拒绝此模型。

四、实证分析

本文选取2010年6月1日至2015年6月11日创业板指数作为研究对象，在样本观测期内，一共有1219个观测值。数据来源于iFind同花顺金融数据库，数据处理使用Eviews6.0、R和Openbugs软件。构建样本数据对数收益率序列得到1218个收益率数据。图1所示为样本期内创业板指数时间序列图以及样本期内的对数收益率曲线。表1给出了我国创业板指数收益率的基本统计量。由表1可知，创业板指数的对数收益率序列呈现明显的尖峰厚尾特征，偏度系数为-0.305，表现出明显的左偏特征；峰度系数为3.79，大于正态分布的峰度系数3，呈现尖峰厚尾的特征；J-B检验的结果显示，样本收益率序列不服从正态分布，这与国外发达市场的股市特征是一致的。

图1　创业板指数时间序列图(上)和收益率时间序列图(下)

均值最大值最小值标准差偏度峰度J-B(P值)收益率0.0011320.065948-0.0862120.019217-0.3053.7950.78(0.00)

对消除均值μ后的收益率序列建立随机波动率模型，为了便于估计，把基本的SV模型变为：

θt=μ+φ(θt-1-μ)+τυt，υt～N(0,1)

其中，θ0～N(μ,τ2)，μ、φ、τ是待估参数。采用Kim等(1998)假设的先验：μ～N(0,0.1)；设φ=2φ*-1，φ*～Beta(20,1.5)；τ2～IGamma(2.5，0.025)，进行20 000次Gibbs抽样，并且丢掉最初4 000次抽样结果，得到参数的估计结果见表2。

表2　SV模型参数估计结果

图2　估计参数的核密度曲线

SV模型中待估参数的核密度曲线见图2，图2显示对应SV模型的参数估计核密度曲线分布比较集中，参数估计效果较好，这说明SV模型估计的效果是比较理想的。

利用SV模型估计得到的波动率σt计算市场风险价值VaRt=μ+Zασt，并与实际发生的损失进行对比，结果见表3。可以看出，在95%、97.5%、99%的置信水平下，LR统计量的值均小于3.841，即均通过了似然比率检验，但同时我们看到在三个不同的置信水平下，检验结果的失败率均低于理论值，这说明基于SV模型计算的VaR倾向于高估市场风险。在95%的置信水平下，VaR的均值为3.19%，因此可以认为在一天持有期内创业板市场的最大损失不超过3.19%的概率为95%。

表3　随机波动模型计算得到的VaR与实际发生的损失的对比关系

本文接下来对创业板指数的对数收益率序列建立GARCH模型，以对MCMC方法估计下的随机波动率模型的结果进行检验。样本偏自相关函数显示对数收益率序列存在显著的1、2阶自相关，以往的研究发现GARCH(1,1)模型已经能够很好的捕捉到金融市场收益率的波动信息，而不需要采用更高阶数的GARCH模型，因此对收益率序列建立AR(2)-GARCH(1,1)模型。得到如下模型：

均值方程和波动率方程中所有估计参数在5%的显著性水平下都是显著的，在对残差序列的检验中，没有任何统计量表明模型的估计是不充分的。利用AR(2)-GARCH(1,1)模型估计得到的波动率计算VaR值，并与实际发生的损失进行对比，表4显示了对比的结果。

表4　AR(2)-GARCH(1,1)模型计算VaR与实际损失的对比图

表4显示，由AR(2)-GARCH(1,1)模型计算的VaR值，在95%置信水平下，VaR的均值为3.21%，97.5%的置信水平下，VaR的均值为3.80%。并且在95%和97.%的置信水平下，实际发生的损失超过VaR的比率与理论值非常接近，均通过了LR检验。但是在99%的置信水平下，LR值(6.455)大于3.841，因此没有通过LR检验。从VaR估计的失败率可以看出，实际失败率大于理论失败率，因此基于GARCH模型计算的VaR倾向于低估市场风险值。

与SV模型相比，在三个不同的置信度水平上，GARCH模型计算的VaR均值比随机波动率模型计算的偏大，但差异极小。考虑到波动因素之后，并与实际发生的损失进行对比，GARCH模型倾向于低估风险，SV模型倾向于高估风险，总体上可以认为两个模型计算的VaR是一致的。

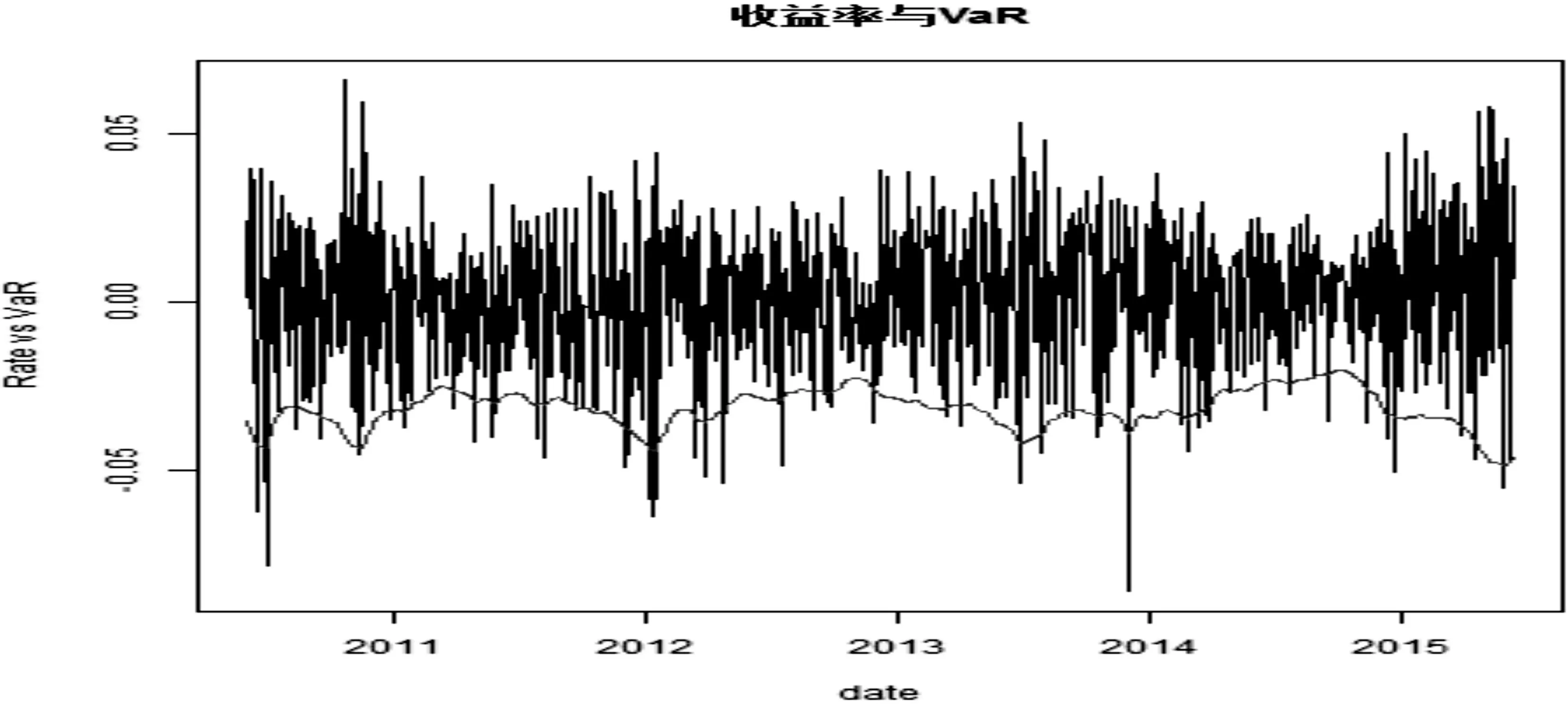
图3　创业板指数收益率与SV模型95%置信水平下计算的VaR

我们以随机波动率模型95%置信水平下估算的VaR为例，研究创业板上市以来的市场风险，图3是对应的收益率曲线图与VaR风险值。图3显示创业板指数出现大幅下跌主要集中在以下几个时间段：(1)2010年6月～2010年8月、(2)2011年12月～2012年4月、(3)2014年11月～至今。第一阶段处于创业板上市初期，创业板自上市以来就表现出了股价大起大落的趋势，开市首日即遭遇爆炒，次日大面积跌停，短暂的价值回归后又历经了近1个月的反弹，股票齐涨共跌、股价大幅度波动的现象，是目前创业板存在的一个突出问题，在这一阶段市场风险明显加剧。第二阶段处于创业板的成长期，业绩不稳定，市场规模比较小，市场波动比较大。第三阶段是2014年6月至今，在国家着重发展股票市场的政策引导下，创业板市场一路高歌猛进，从最初2000点附近一路拉伸到5000多点，市场不理性因素增加，投机风潮席卷整个股票市场，但是脱离市场基本面的虚假上涨导致了创业板指数的巨幅振荡，市场频频出现千股跌停的壮观现象，市场风险也因此急剧增大。

五、结论

本文采用基于MCMC参数估计的随机波动率模型、GARCH模型对创业板指数收益率的波动特征进行刻画，并将市场波动特征考虑进市场风险价值(VaR)的计算。实证结果显示：SV模型和GARCH模型计算的VaR值非常相似，但是SV模型倾向于高估市场风险，GARCH模型倾向于低估市场风险。并且在一天持有期内，在95%的置信度下，创业板市场发生的最大损失不会超过3.19%；在99%的置信度下，创业板市场的最大损失不会超过4.45%。本文的研究结果对创业板市场的风险管理具有重要的指导意义。

参考文献：

[1]Jorion Philippe,Risk:Measuring the risk in value at risk[J],Financial Analysts Journal,1996,Dec/Nov:47-561.

[2]Lee T H,Saltoglu B.Assessing the risk forecasts for Japanese stock market[J].Japan and the World Economy,2002,14(1):63-85.

[3]Marimoutou V,Raggad B,Trabelsi A.Extreme value theory and value at risk:application to oil market[J].Energy Economics,2009,31(4):519-530.

[4]郑文通.金融风险管理的VaR方法及其应用[J].国际金融研究，1997(9):58-62.

[5]王春峰，万海辉，李刚.基于MCMC的金融市场风险VaR的估计[J].管理科学学报，2000,3(2):54-61.

[6]陈雪华，杨辉耀.VaR——一种风险度量的方法[J].广州大学学报(自然科学版),2002,1(2):8-12

[7]黄宇红.基于GARCH类模型的权证时变VaR值估计[J].上海管理科学，2009(6):9-13

[8]Tasy R S.金融时间序列分析[J].2009(2).

The Measurement and Analysis of the Market Risk of the GEM in China——Empirical Research Based on Stochastic Volatility Model

HUANG Xiu-hai,GONG Yong-xu

(SchoolofMathematicsandStatistics,ZhejiangUniversityofFinance&Economics,Hangzhou,Zhejiang310018)

Abstract：The high risk of the Growth Enterprise Market(GEM)has always been the significant point of the academia and the practice field.In order to measure the market risk of the GEM accurately,the author of this article introduces the MCMC parameter estimation method to SV model to calculate the VaR.The results show that:within one-day holding period,under the circumstance of 95% confidence level,the largest loss of GEM would not exceed 3.19%.Meanwhile,under the circumstance of 99% confidence levels,the largest loss of GEM would not exceeds 4.45%.Besides,the author also employs the GARCH patterns to assist the research on the risk of GEM.

Key words：GEM;MCMC;stochastic volatility model;VaR

中图分类号：F064.1

文献标识码：A

文章编号：1671-9743(2016)02-0028-05

作者简介：黄秀海，1966年生，男，湖南麻阳人，副教授，博士，研究方向：经济学；

基金项目：国家社会科学基金项目“聚类分析视角的多层次CPI指数构建研究”(14BTJ023)；全国统计科学研究计划项目“多层次CPI指数编制研究……以杭州市居民生活消费品面板数据为例”(2013LZ43)；浙江财经大学校级课题一般项目(98)。

收稿日期：2015-11-20

龚泳旭，1989年生，男，湖南人，硕士生，研究方向：经济学。