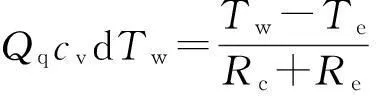基于反褶积的地热井井底压力响应计算方法

李　静,　王　磊,　何　桃,　龙鹏程,　江　平

(1.合肥工业大学 数学学院,安徽 合肥　230009; 2.中国科学院 核能安全技术研究所,安徽 合肥　230031)



基于反褶积的地热井井底压力响应计算方法

李静1,王磊2,何桃2,龙鹏程2,江平1

(1.合肥工业大学 数学学院,安徽 合肥230009; 2.中国科学院 核能安全技术研究所,安徽 合肥230031)

摘要:文章提出了一种根据地热井放喷试验数据计算井底压力响应的方法,解决了放喷试验数据无法进行分析的难题,计算出的井底压力数据反映了地层流动特征,可用于试井分析和产能预测。由于地热井井筒温度、压力变化较大,在计算井筒压力损失时根据流体、水泥环、地层的耦合传热,推导热量损失的微分方程,给出了一种井筒温度、压力、密度分布的计算方法,使计算出的井筒压力损失较准确。在计算井底压力响应时,使用基于反褶积的总体最小二乘方法根据变流量条件下的井底压力计算出单位流量下的井底压力响应,同时把测量误差纳入了目标函数。最后对国内某地热井地面放喷试验数据进行了分析,根据计算出的井底压力响应预测了不同开采条件下的产能,预测的长时间开采时的产量与放喷测试获得的稳定流量吻合,验证了方法的正确性和实用性。

关键词:地热开发;放喷试验;井底压力计算;井筒温度分布;反褶积

作为一种可再生的清洁能源,地热能逐渐受到各国重视。我国地热使用量居世界第一,但多为浅层地热利用,中深层地热开发技术相对落后,效率较低[1]。为实现地热井的科学开采,需要进行流动动态分析和预测,具体步骤为:进行现场测试获取反映地层流动特征的压力、流量等数据,然后通过试井分析等手段获取地层参数,建立流动模型,最后根据流动模型预测未来生产动态,指导生产。

油气藏的试井分析和产能预测方法发展已比较成熟[2-4],在石油行业已进行了多年应用,一般是进行瞬态压力测试获得定产量条件下的井底压力响应,通过试井分析获取井周围的储层流动参数,使用这些参数进行产能预测。热储和油气藏中的流动过程相似,可借鉴油气藏试井分析方法对地热井进行试井分析。地热井一般通过地面放喷试验测量井口压力、流量数据[5],如图1所示。由于放喷时对空气敞喷,没有施加约束,流量随时间不断变化,相当于变产量生产,不满足常规试井分析要求的定产量生产条件。如果能够根据放喷试验数据计算出定产量条件下的井底压力响应,则可利用成熟的试井分析和产能预测方法进行生产动态预测。

图1　地热井放喷试验管路示意图

文献[6]首次利用变产量下的压力数据反演计算出了定流量下的压力响应数据,文献[7]也做了类似工作,但上述方法不仅计算复杂而且数值稳定性差。文献[8]提出了数值拉普拉斯变换使得复杂的反褶积运算变成了简单的乘除运算,但其数值稳定性仍没有提高;文献[9-10]提出了一种时间域上的油气藏井底压力反褶积处理方法,使反褶积方法数值稳定性得到明显提高。

虽然上述方法已在油气井中进行了应用,但它们只能处理井底压力数据,无法处理地热井放喷试验测得的井口压力,而根据地热井放喷数据计算井底压力响应的方法研究较少。方法的缺失使得放喷试验只能观察长时间放喷后的稳定流量,前期大量动态数据无法利用。因为没有方法计算地热井的井底压力响应,使得无法通过试井分析建立地层流动模型,也不能进行产能预测。地热井井筒中温度、压力变化较大,必须先计算井筒中温度、压力分布,才能得到准确的井筒压力损失,进而将井口压力折算到井底,再通过反褶积得到单位流量下的压力响应。

本文在中国科学院核能安全技术研究所FDS团队[11-20]的支持下提出了一种根据地热井放喷试验数据计算井底压力响应的计算方法,解决了放喷试验数据无法进行分析的难题。方法分为2部分：在计算井筒压力损失时,给出了一种井筒温度、压力分布的计算方法,根据温度、压力计算不同深度的密度,以获得较准确的井底压力;在计算井底压力响应时,使用基于反褶积的总体最小二乘方法根据变流量条件下的井底压力计算出单位流量下的井底压力响应,同时考虑了测量误差的影响。最后对国内某地热井地面放喷试验测试数据进行了分析,验证了方法的正确性和实用性。

1井筒压力损失计算

地热井的放喷试验中,压力、流量、温度等仪表放置在井口,测得的是井口处的压力和流量,而试井分析需要的是井底压力,所以首先需要计算井筒压力损失,获得井底压力。一般地热井的井筒中水为液态,流动过程中不发生相态变化,产生压力损失的主要因素为:① 井筒管壁摩擦阻力;② 向地面流动过程中克服重力做功。

1.1管壁摩阻造成的压力损失

根据达西公式[21],管壁摩阻造成的压力损失计算公式为:

(1)

其中,pf为管壁压力损失;ρ为流体密度;λ为管壁摩擦系数,其值取决于流体在管道内流动状态和管壁的粗糙程度;l为管道长;v=4q/(πd2)为管道中有效截面上的平均流速;q为流量;d为管道计算内径。

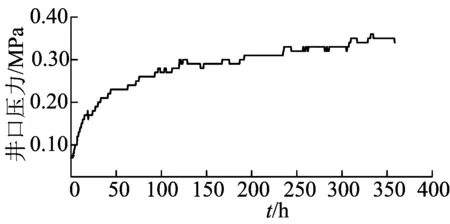
管壁摩擦系数λ可使用柯列勃洛克公式计算,如(2)式所示,(2)式对4 000

(2)

其中,Δ为管壁粗糙度;Re为雷诺数。

对60 ℃的地热水,以0.028 m3/s(100 m3/h)的流量在直径为0.34 m的井筒中流动时,雷诺数约为219 500,流态为紊流,如管壁粗糙度取0.000 1 m,根据(2)式计算的管壁摩擦系数λ为0.009 6。对于1 000 m长的井筒,管壁摩擦阻力造成的沿程损失为1.32 kPa,而静液柱压力约为9.63 MPa,管壁摩阻损失仅为静液柱压力的0.014。可见,管壁摩阻在计算井筒压力损失时可忽略不计。

1.2重力造成的压力损失

在热水从井底流向井口的过程中,需要克服重力做功,产生较大的压力损失,在忽略管壁摩阻的条件下,可用静液柱压力计算克服重力做功造成的压力损失,即

(3)

其中,pg为静液柱压力;ρ为流体密度;gh为重力加速度;h为井筒液柱高度。

如果流体密度不为常数,需要使用积分计算液柱压力,如(4)式所示:

(4)

井筒不同深度的温度和压力变化较大,水的密度也会发生变化,需要计算出沿井筒的温度和压力分布,代入PR、BWR[22]等状态方程计算密度。

一种简单的井筒温度计算方法是忽略套管的热传导(套管厚度小且热导率高),将水泥环的传热按稳态传热处理,地层的传热按瞬态传热处理,并使用Ramey函数[23]简化地层传热过程。则井筒单位长度上的热损失为:

(5)

其中,Qloss为井筒单位长度上的热损失;Tw为井筒温度;Te为地层温度;Rc为水泥环的热阻;Re为地层的热阻。

地层温度T可由测井资料获得或地层静温梯度计算,水泥环的热阻计算公式为:

(6)

其中,rco为水泥环外径;rci为水泥环内径;λc为水泥环的热导率。

地层热阻的计算公式为:

(7)

(8)

其中,f(t)为Ramey函数;λe为地层的热导率;t为测试时间;α为地层热扩散系数。

忽略垂向上的热量传递,由(5)式可建立计算井筒温度分布的微分方程:

(9)

其中,Qq为水的质量流量,可由井口压力、温度和体积流量计算;cv为水的比热容;h为井深。

在实际计算中,将井筒按深度均分为n个点,具体计算步骤为:

(1) 使用(9)式计算每个点的温度,即T1,T2,…,Tn。

(2) 井口的温度T0和压力p0由测量数据获得,根据水的状态方程计算该处的密度ρ0。

(3) 已知第i点的压力pi和密度ρi后,使用液柱压力计算第i+1点的压力pi+1,再根据水的状态方程计算第i+1点的密度ρi+1,pi+1的计算公式为：

(4)重复步骤(3),直到计算出所有点的压力和密度。

(5) 第n点的压力pn即为井底压力,pn-p0为井筒压力损失。

根据井筒压力损失和地面放喷试验的井口压力数据,可得折算后的变流量下的井底压力为:

(10)

其中,ph(t)为地面放喷试验测试的井口压力。

2井底压力数据计算方法

地热井放喷试验中一般不使用高精度的压力计和流量计,而是使用压力表和流量表,特别是有些放喷试验中使用三角堰测量流量,精度较低,在井底压力的计算方法中需要考虑实测数据误差的影响。在同时考虑压力和流量误差的前提下,本文的方法可以根据地面放喷试验中变产量下的井口压力数据计算单位流量下的井底压力响应。

由杜哈美(Duhamel)原理知[8]:

(11)

(12)

其中,p0为原始地层压力;pwf为计算出的测试时间t时的井底压力;q为实测流量;g为单位产量时井底压力G的导数。

地热井测得的是井口压力,把(10)式代入(11)式得:

(13)

其中

(14)

压差Δpwf是q与g的褶积,试井测试中测得了q,通过井筒压力计算可得到Δpwf,需要求解单位产量时的井底压力导数g,是一个反褶积求解问题。

试井分析需要的是井底压力对对数时间的导数,不需要直接计算函数g,为此定义如下2个新变量:

(15)

把(15)式代入(13)式得:

(16)

则求压力响应函数g的问题就转化为求Z随τ的变化关系,即Z(τ)的函数式。

假设流量为阶梯状变化,其流量插值函数为:

(17)

其中,系数qj是测试区间[aj,bj]内实际测得的流量;θj(t)为流量插值函数,定义如下:

(18)

再设w个不同时刻的函数值zk(反映了地层流动特征),通过线性插值可以得到Z(τ)的表达式为:

(19)

(20)

将(17)式、(19)式代入(16)式可得到给定流量时的井底压力差,写成矩阵形式为:

(21)

其中,q=(q1,…,qN);C是一个响应函数系数的矩阵。

(22)

再设ε为地热井地面放喷试验井口压力的测量误差,δ为流量测量误差,则杜哈美(Duhamel)原理变为:

(23)

把反褶积求解作为总体最小二乘最优问题考虑,记误差目标函数为:

(24)

其中,ε和δ分别为压力误差和流量误差;D和k分别为常数矩阵和常数向量；Dz-k为曲线光滑度;a和b为加权系数。当E最小时即为最小二乘问题的最优解,对应于本文所测的地面放喷测试井口数据,则误差目标函数为:

(25)

其中,p0为原始地层压力;ph(t)为放喷测试井口压力数据;YM为单位向量;pg为井筒压力损失;y为真实流量。记x′=[p0-pg,y],x″=z,则(25)式可改写成:

(26)

其中

(27)

(28)

令r(x′,x″)=F(x″)x′-l(x″),则求解E的最优值问题是数学上一种典型的可变量分离最小二乘问题,使用变量分离投影算法[24]和拟牛顿法可求得E的最优值Z,再通过相应的数学运算即可求出单位流量下井底压力G,也就是通过反褶积运算把变流量下的井底压力数据转化为了单位产量下的井底压力响应。

3实例分析

对国内某地热井的地面放喷试验数据进行分析,测得的井口压力如图2所示。该井由于没有放喷数据的计算方法,无法获得井底压力响应,进行动态预测,只能通过长时间放喷得到一个稳定流量,增加了测试成本。测试结束时的稳定流量为49 m3/h,且仍随时间缓慢减少。

通过本文提出的基于反褶积计算地面放喷试验井底压力响应方法计算出了单位产量下的井底压力。由于单位产量下压力变化较小,本文给出的是井底压力与原始地层压力的差,结果见表1所列,如图3所示。

图2　井口压力随时间变化

序号t/h压力差/Pa序号t/h压力差/Pa10.50262.712660.00351.5121.00275.992765.00352.9731.50283.332869.00353.9442.00288.712980.00356.8653.00296.033090.00358.8063.50298.9531100.00361.2374.00301.3932110.00362.6984.50303.3433120.00364.1595.00305.7734130.00365.61105.50307.2335140.00367.07116.00308.6936150.00368.53128.00314.0537160.00369.501310.00318.4338170.00370.571413.00323.3039180.00371.931516.00326.7040190.00372.901617.00328.1641200.00373.881720.00331.0842210.00374.851824.00334.4943230.00376.311928.00337.4044250.00377.772032.00339.8445260.00378.262136.00341.7846270.00379.222240.00343.7347300.00381.172345.00346.1648325.00382.432450.00348.1049350.00384.092555.00350.0550360.00384.57

图3　单位产量下的井底压力差

压力导数与时间的乘积如图4所示,从图4可以看出,地层表现出均质无限大地层特征。

图4　单位产量下的井底压力导数

把图3所示的单位流量下的井底压力差输入试井软件进行试井分析,发现流动区域为均质无限大地层,渗透率约为140 mD。根据分析出的地层参数可进行产能预测,图5所示给出了该井井底压力分别为12.15、12.30、12.45 MPa时的产量变化曲线,从图5中可知,井底压力为12.45 MPa时生产1 a后的产量约为285 m3/d,井底压力为12.15 MPa时生产1 a后的产量约为1 870 m3/d,井底压力越低则产量越高。

图5　不同压差下产量随时间变化

实际生产时的井底压力约为12.30 MPa,根据图5预测的曲线连续生产720 h时的流量为49.81 m3/h,与实测的稳定流量吻合较好,说明使用本文方法计算得到的井底压力响应反映了地层流动特征,动态预测结果与实际情况相符,验证了方法的正确性和实用性。

4结束语

本文提出了一种根据地热井放喷试验数据计算井底压力响应的计算方法,解决了放喷试验数据无法进行分析的难题,使用该方法可根据井口数据计算单位流量下的井底压力响应,计算结果反映了地层流动特征,可用于试井分析和产能预测。

在计算井筒压力损失时,对比了管壁摩阻和液柱压力的影响,认为管壁摩阻可忽略,给出了一种井筒温度、压力分布的计算方法,考虑了密度变化的影响,可获得较准确的井底压力;在计算井底压力响应时,使用基于反褶积的总体最小二乘方法根据变流量条件下的井底压力计算出单位流量下的井底压力响应,并将压力和流量数据的测量误差纳入最小二乘目标函数计算。最后对国内某地热井地面放喷试验测试数据进行了分析,验证了方法的正确性和实用性。

在该方法基础上进一步研究的方向是使其能够计算地热井开采中测得的低精度、低频率的生产数据,获得井底压力响应,为地热勘探、开发决策提供科学依据,减少风险,提高经济效益。

[参考文献]

[1]张金华，魏伟，杜东，等.地热资源的开发利用及可持续发展[J].中外能源，2013，18(1):30-35.

[2]王磊.多层油藏渗流规律研究及其应用[D].合肥:中国科学技术大学，2008.

[3]曾亿山，晏忠良，陈峰磊.油藏数值反演数学模型的研究[J].合肥工业大学学报:自然科学版,2005,28(10):1268-1272.

[4]王蕾.试井数据预处理与模型诊断技术研究[D].西安:西安石油大学，2013.

[5] GB/T 11615-2010,地热资源地质勘查规划[S].

[6]Jargon J R，Van Poolen H K.Unit response function from varying-rate data[J].Journal of Petroleum Technology，1965，17(8):965-969.

[7]Bostic J N，Agarwal R G.Combined analysis of postfracturing performance and pressure buildup data for evaluating an MHF gas well[J].Journal of Petroleum Technology，1980，32(10):1711-1719.

[8]Roumboustsos A，Stewart G，Heriot-Watt U.A direct deconvolution or convolution algorithm for well test analysis[C]//SPE Annual Technical Conference and Exhibition.Houston:Society of Petroleum Engineers，1988:487-502.

[9]Schroeter T，Hollaender F，Gringarten A.Analysis of well test data from permanent downhole gauges by deconvolution [C]//SPE Annual Technical Conference and Exhibition.San Antonio:Socity of Petroleum Engineeers,2002:1-13

[10]Schroeter T，Hollaender F，Gringarten A.Deconvolution of well test data as a nonlinear total least square problem[J].Scoiety of Petroleum Engineers Journal，2004，9(4):375-380.

[11]孔详言.高等渗流力学[M].合肥:中国科学技术大学出版社，2010:40-50.

[12]Wu Y C，FDS Team.Conceptual design activities of FDS series fusion power plants in China[J].Fusion Engineering and Design，2006，81(23/24):2713-2718.

[13]吴宜灿，李静惊，李莹，等.大型集成多功能中子学计算与分析系统VisualBUS的研究与发展[J].核科学与工程，2007，27(4):365-373.

[14]吴宜灿，黄群英，朱志强，等.中国系列液态锂铅实验回路设计与研发进展[J].核科学与工程，2009，29(2):161-169.

[15]Wu Y C，FDS Team.CAD-based interface programs for fusion neutron transport simulation[J].Fusion Engineering and Design，2009，84 (7/8/9/10/11):1987-1992.

[16]Wu Y C，Xie Z，Fischer U.A discrete ordinates nodal method for one-dimensional neutron transport calculation in curvilinear geometries[J].Nuclear Science and Engineering，1999，133(3):350-357.

[17]Wu Y C，FDS Team.Conceptual design of China fusion power plant FDS-II[J].Fusion Engineering and Design，2008，83 (10/11/12):1683-1689.

[18]Wu Y C，FDS Team.Conceptual design of and testing strategy of dual functional lithium-lead test blanket module in ITER and EAST [J].Nuclear Fusion，2007，41 (11):1533-1539.

[19]Cao R，Wu Y C，Pei X，et al.Multi-objective optimization of inverse planning for accurate radiotherapy[J].Chinese Physics C，2011，35(3):313-317.

[20]吴宜灿，刘萍，胡丽琴，等.大型集成概率安全分析软件系统的研究与发展[J].核科学与工程，2007，27(3):270-276.

[21]吴宜灿，柏云清，宋勇，等.中国铅基反应堆概念设计研究[J].核科学与工程,2014，34(2):201-208.

[22]喻西崇，赵金洲，邬亚玲，等.PVT状态方程的选择和分析[J].油气储运，2001，20(09):24-25.

[23]Ramey H J.Wellbore heat transmission[J].JPT，1962(4):427-435.

(责任编辑马国锋)

Geothermal well bottom hole pressure response calculation based on deconvolution

LI Jing1,WANG Lei2,HE Tao2,LONG Peng-cheng2,JIANG Ping1

(1.School of Mathematics， Hefei University of Technology， Hefei 230009， China; 2.Institute of Nuclear Energy Safety Technology， Chinese Academy of Sciences， Hefei 230031， China)

Abstract:In this paper, a method to calculate well bottom hole pressure response with the data of geothermal well open flow test is presented. The method solves the problem that the open flow test data is not suitable for conventional well test analysis methods， and the analysis result reflects the formation flow characteristics and can be used for well test and productivity prediction. Because the well bore temperature and pressure are rather changeable， the coupled heat of fluid， cement sheath and formation is considered when calculating the well bore pressure drop, and the differential equation of heat loss is deduced. The method accounts for uncertainties including the true error and the pressure drop caused by the temperature， pressure and density distribution. The well bottom hole pressure response under the condition of unit flow rate is calculated according to the well bottom hole pressure under the condition of variable flow rate by using the total least squares method based on deconvolution. Finally， the open flow test data of a domestic geothermal well is treated by the method and the productivity under different exploitation conditions is provided by using the calculated well bottom hole pressure response. The predicted productivity under long time exploitation accords with the steady flow rate obtained by the open flow test, which verifies the correctness and practicability of this method.

Key words:geothermal development; open flow test; well bottom hole pressure calculation; well bore temperature distribution; deconvolution

中图分类号:TK521.2

文献标识码：A

文章编号：1003-5060(2016)03-0421-06

doi:10.3969/j.issn.1003-5060.2016.03.025

作者简介：李静(1989- )，女，河南鹤壁人，合肥工业大学硕士生；

基金项目：国家自然科学基金资助项目(91026004;11305205)

收稿日期：2015-01-30；修回日期：2015-04-20

江平(1972- )，女，安徽安庆人，博士，合肥工业大学副教授，硕士生导师.