基于SEA的AGA-SVR节假日客流量预测方法研究

陈荣梁昌勇葛立新

(1.蚌埠学院经济与管理学院，安徽蚌埠233030;

2.合肥工业大学管理学院，安徽合肥230009;3.蚌埠学院理学院，安徽蚌埠233030)

基于SEA的AGA-SVR节假日客流量预测方法研究

陈荣1梁昌勇2葛立新3

(1.蚌埠学院经济与管理学院，安徽蚌埠233030;

2.合肥工业大学管理学院，安徽合肥230009;3.蚌埠学院理学院，安徽蚌埠233030)

节假日旅游客流量由于游客在短期内大量集中于同一地点、不同节假日休假时间长短、所处季节等不同，呈现复杂非线性特征和明显季节性特点。本文提出一种基于季节指数调整(Seasonal Exponential Adjustment，SEA)的自适应遗传算法(Adaptive Genetic Algorithm，AGA)－支持向量回归(Support Vector Regression，SVR)预测模型，即基于SEA的AGA-SVR模型，并用国内著名5A级风景区黄山2008～2012年节假日客流量数据对模型进行验证。研究结果表明，基于SEA的AGA-SVR预测模型能够准确处理节假日旅游客流量预测中的非线性和季节性问题，较AGA-SVR和GASVR等方法具有更高的预测精度，在旅游预测领域应用前景广阔。

季节指数调整;支持向量回归;自适应遗传算法;节假日旅游客流量预测

0 引言

2008年我国实行新的休假制度，将每年节假日休假定为元旦、春节、清明节、端午节、劳动节、中秋节和国庆节，每年休假天数共计29天。新休假制度的实施带动了假日经济、假日旅游的兴起，成为我国国民经济新的增长点，但同时也带来一系列问题:大量游客在同一时间集中于同一地点，造成景区超载、交通拥挤、住宿紧张、服务质量下降、安全隐患增多等问题。近年来九寨沟、华山、张家界、黄山等景区频繁发生的节假日游客拥堵事件，给旅游景区造成了很大的负面影响。准确的节假日客流量预测能够使景区管理部门提前决策，有效避免此类事件发生。但是由于各节假日所处季节不同、休假时间长短不同，节假日旅游客流量除了由一年四季等自然因素形成的自然季节性外，还存在由节假日等制度因素而造成制度季节性。两种季节性的叠加对节假日客流量的准确预测产生很大的影响(Song，Li，2008)。因此如何进行季节调整、实现准确预测一直是文献研究关注的重点。

目前季节调整的方法，一种是以自回归移动平均模型(Autoregressive Integrated Moving Average，ARIMA)为基础的季节处理方法，如季节自回归移动平均模型(Seasonal Autoregressive Integrated Moving Average，SARIMA)方法，Huang和Min (2002)利用该种方法实现了对季节性的处理;此外，X-11-ARIMA和X-12-ARIMA等方法也常被用来进行季节调整(Shiskin，et al.，1967;Findley，et al.，1998)。该类方法主要通过差分的方式来消除季节性的影响，但实践证明，差分只对消除线性趋势的季节性有效(Nelson，Plosser，1982)，对非线性趋势明显的季节性，以ARIMA为基础的方法预测精度明显不足;而且以ARIMA为基础的季节处理方法，缺乏明确的关于原时间序列的分解模型，必须要事先设定好模型形式，因而在实际运用过程中，无法知道数据的真正形成过程，不能正确把握客流量性质(Zhang，Qi，2005)。季节调整的另一种方法为季节指数调整方法(Seasonal Exponential Adjustment，SEA)，这是一种对原始数据直接进行季节处理(data deseasonalization)的方法，它通过季节指数来修正原始数据及预测结果，使其更符合实际数据变化的客观规律。通过SEA，原始数据的季节性得到调整及消除。Gardne和McKenzie(1989)、翁钢民和李凌雁(2014)通过研究发现，利用该方法对数据进行季节处理，预测的准确性大大提高;Tseng等人(2002)的研究显示，当SEA方法和其他预测方法组合进行预测时，预测效果均好于不使用SEA方法。

另一方面，节假日旅游客流量除了季节性特点之外，非线性趋势明显。传统时间序列预测方法对具有线性特征的旅游客流量有较好的预测效果，但对于复杂的非线性旅游客流量预测往往难以实现。人工神经网络(Artificial Neural Network，ANN)为非线性旅游客流量预测提供了一种方法，但难以克服自身局部最优等缺点，且ANN方法往往需要大样本训练，国内各大景区由于实现数字信息化时间短，难以获得所需要的大量样本，因此ANN方法往往达不到所需的预测精度。SVR作为一种统计学习理论方法，克服了传统时间序列预测方法和ANN的上述缺点，在解决非线性、小样本旅游客流量预测方面表现出许多特有的优势，逐渐成为学者们预测旅游客流量的一种重要工具，预测效果明显优于ARIMA、ANN等方法(Chen，Wang，2007;Cai，et al.，2009;Chen，2011)。虽然SVR在非线性预测方面表现出特有优势，但在处理季节性方面仍有一定不足。因此建立一个科学准确的、能够同时处理季节性和非线性的节假日客流量预测模型，可为旅游景区在节假日旅游高峰期分流游客、科学调度提供直接信息，对旅游风景区尤其是热门景区乃至整个旅游行业意义重大。

由于SVR预测精度受其自由参数(C，ε，σ)影响，Chen等(2007)将遗传算法(Genetic Algorithm，GA)和SVR结合实现客流量预测，效果虽优于反向传播神经络(Back-Propagation Neural Network，BPNN)方法，但是GA存在过早收敛、局部最优等问题。AGA克服了GA的缺陷，已有研究表明，将AGA和SVR结合可以实现准确预测(Zhang，et al.，2014)。因此，本文引入AGA实现对SVR参数的自适应寻优，将SEA、AGA和SVR这3种工具结合，建立基于SEA的AGA-SVR预测模型，实现对季节性、非线性的节假日旅游客流量的预测。

1 基于SEA的AGA-SVR模型原理

1.1SEA过程

步骤1在时间t的客流量xt可表示为季节成分与趋势成分的乘积，则季节指数Is为:

步骤2用每一个周期中xi的均值作为趋势成分近似值，重新对数据集x1，x2，…，xT排列为:x1l，x2l，…，x1l，…;xk1，xk2，…，xkl，…;xm1，xm2，…，xml。k=1，2，…，m;s=1，2，…，l;T=m×l，m为周期数，l为周期内数据数目。

步骤3计算每个周期的均值，然后将数据xks标准化，计算季节指数Ij，即:

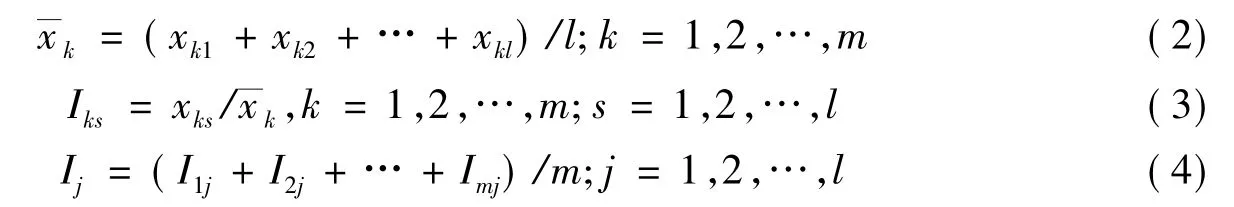
因为

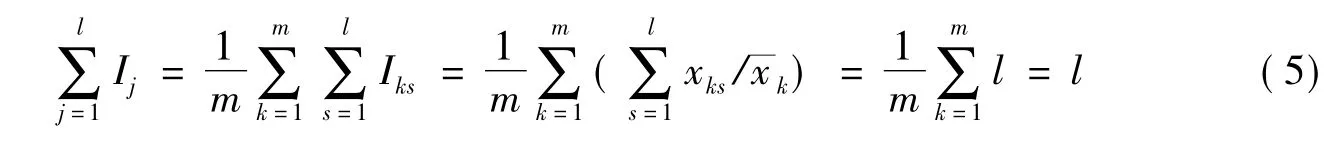
所以季节指数Ij遵循标准化的定义。

步骤4利用季节指数Ij，消除过季节影响因素的新数据为:

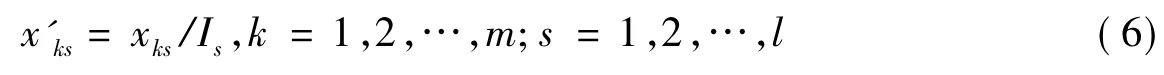
再重新排列数据集x'11，x'12，…，x'1l，…;x'k1，x'k2，…，x'kl，…;x'm1，x'm2，…，x'ml得到了经过季节指数调整的新数据集。具体流程如图1所示(ave表示均值)。

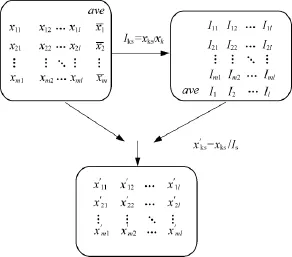
图1 季节指数调整(SEA)流程

1.2SVR原理

SVR主要原理是通过一个非线性变换x→(x)将训练样本映射到高维空间，在高维空间通过核函数实现线性变换(Vapnik，2009)。设给定的训练样本(xi，yi)，i=1，2，…，n;xi=Rn;yi∈R;xi为输入向量;yi为xi相对应的输出值;n为训练样本个数，SVR根据如下式子来对回归函数进行估计:

由结构风险最小化原则可知，下式即为寻求使风险最小的f:

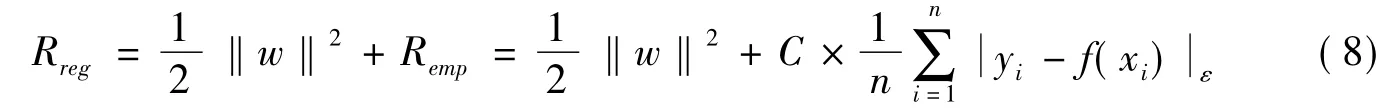
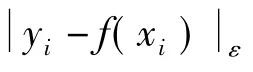
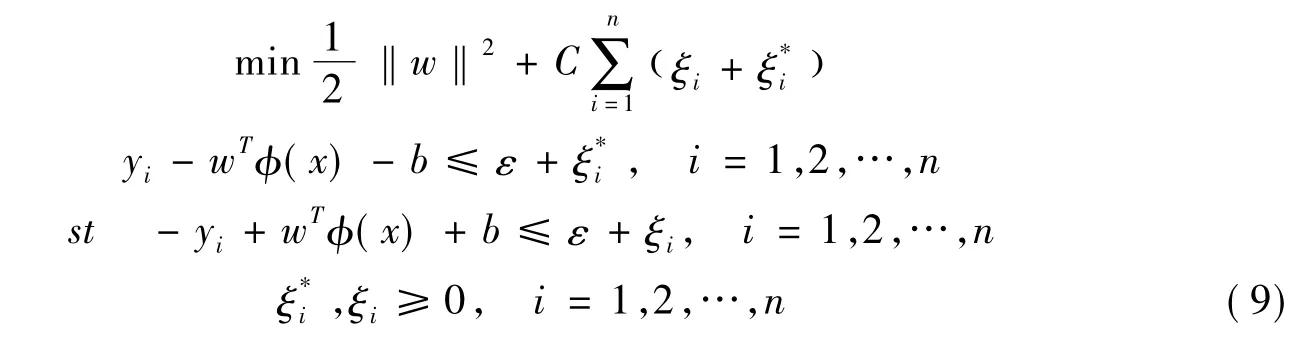
通过引入Lagrange函数和KKT(Karush-Kuhn-Tucker)条件(Vapnik，2009)，最后得到回归函数f(x)的表达式为:

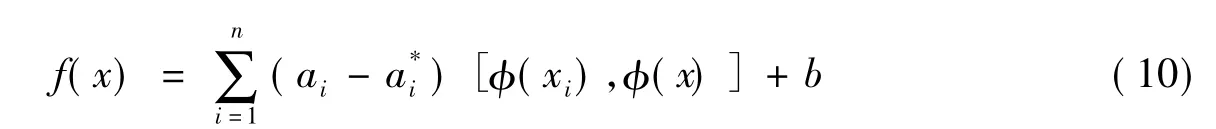
ai，为Lagrange乘子。根据节假日客流量非线性特点，本文选取Gaussian RBF为核函数，即:

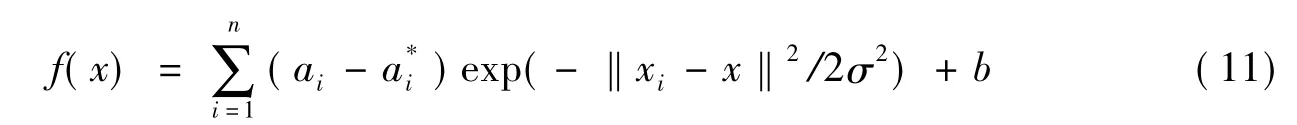
上式中σ为核的宽度，xi为训练集输入值，x为测试集输入值。

1.3 AGA算法寻优原理

AGA克服了经典GA的无法收敛到全局最优、染色体易丢失和过早收敛等问题(许光泞，等，2007)。它的主要原理是交叉和变异概率pc、pm随种群适应值自适应变化(Srinivas，Patnaik，1994)。具体过程如下(王万良，等，2004):

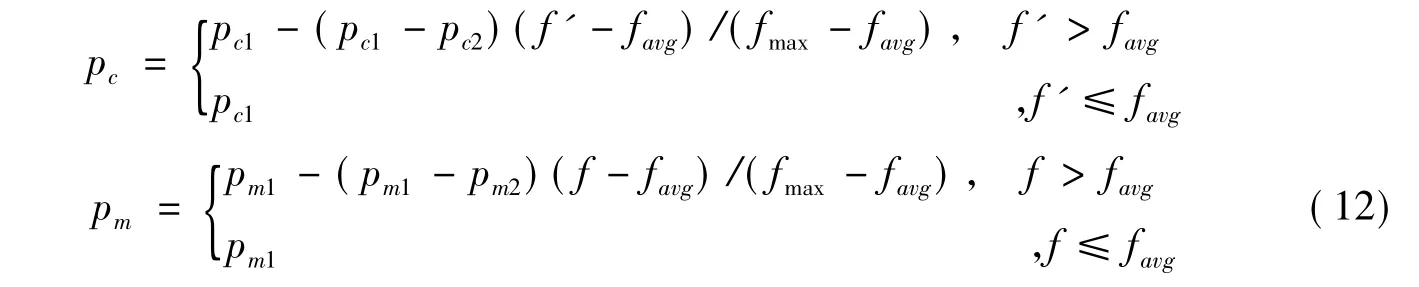
其中，favg表示为每代群体平均适应值，fmax分别表示每代群体中个体最大适应值，f为被选择变异个体适应值，f'为被选择交叉的两个个体中较大适应值;pc2、pm2均非零，分别为群体中最大适应值个体的交叉概率和变异概率。由(12)知，如f'=fmax，f=fmax，则pc= pc2，pm=pm2。算法采用精英保留策略，将每一代的优良个体直接复制到下一代中。

1.4 基于SEA的AGA-SVR模型建模过程

步骤1归一化季节指数调整数据。根据式(2)～(6)，按照图1流程顺序，对原始数据进行季节指数调整，将消除季节因素的新数据进行归一化，再根据预测需要将新数据分为训练集、测试集，并分别输入模型。

步骤2种群初始化。将SVR参数(C，ε，σ)编码为染色体X，即X={C，ε，σ}，对其随机初始化。

步骤3适应值评估。用训练集对初始化的SVR参数对进行训练，参数优化准则采用交叉验证(Cross Validation，CV)。选取均方误差(Mean Square Error，MSE)为适应值函数(杜京义，侯媛彬，2006):

这里yi分别为实际值和预测值，n是测试样本个数。通过(13)式计算SVR参数适应值f，以f值作为选取参数的标准。同时根据轮盘赌方法选择N个个体(N为偶数)，计算群体favg、fmax。

步骤4交叉和突变。根据公式(12)计算自适应pc和pm，以pc和pm分别进行交叉和突变，随机产生R(0，1)，若R小于pc、pm，则对SVR参数(C，ε，σ)进行交叉和突变。

步骤5最优策略。计算通过交叉、变异产生的新个体f值，新个体同父代共同组成新一代种群，若新种群产生的最小f值较老种群的小，则替换老的染色体。

步骤6停止准则。若被执行代数和指定代数相等(这里进化代数设置为100)，则结束，同时将获得的最优参数(C，ε，σ)带入SVR预测。否则转向步骤3。

步骤7预测值季节调整。将AGA-SVR预测值乘以季节指数(Is)，得到经过季节调整的预测值。具体的模型流程图见图2。

图2 基于SEA的AGA-SVR模型流程图

2 实例研究

2.1 数据来源

本文数据来源于黄山风景区信息中心。数据显示，2008～2012年，黄山风景区节假日(元旦、春节、清明节、端午节、劳动节、中秋节和国庆节)客流总量占全年客流总量的百分比分别为15.01%、13.05%、15.79%、18.71%和15.56%，客流量在短期内聚集，多而集中，给景区的资源和调度等工作造成很大的压力。因此本文选取黄山风景区2008～2012年4年间每年所有节假日每日数据作为研究对象，具有重要的代表性。该数据集包括:每年所有节假日每日客流量、每年所有节假日每日上午8点前客流量和每年所有节假日每日人体舒适度指数(Human Comfort Index，HCI)，分别定义为{X1，X2，X3}，其中每个变量包含数据的个数为145。具体如图3、图4所示。

图3 2008～2012年节假日每日客流量

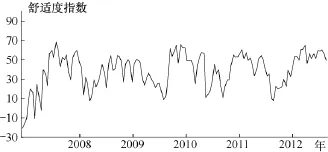
图4 2008～2012年节假日每日人体舒适度指数(HCI)

由图3、图4可知:

(1)不同的节假日休假时间长短不同，客流量的波动情况不同，每个节假日均呈现明显“两头低中间高”现象，非线性趋势明显;

(2)由于气候、消费者每年相同旅游行为等因素影响，每年节假日客流量数据呈现出明显的季节性和年度周期性的特征，大体表现为“三峰三谷”特点;

(3)每日8点前客流量、每日人体舒适度指数对每日客流量产生重要影响，可将这两个因素作为客流量的影响因素。

2.2 数据处理

按照图2流程，首先对原始数据集进行SEA处理，计算出每个节假日每天的季节调整指数(Is)(见表1)。然后根据(7)式，对2008～2012年节假日每日客流量、每日8点前上山客流量及每日人体舒适度指数进行季节指数调整。调整后的数据如图5、图6所示。可以看出，经过季节指数调整，每日客流量、每日8点前上山客流量及每日人体舒适度指数等数据波动幅度降低，数据集的季节性得到消除，呈现典型非线性特点。

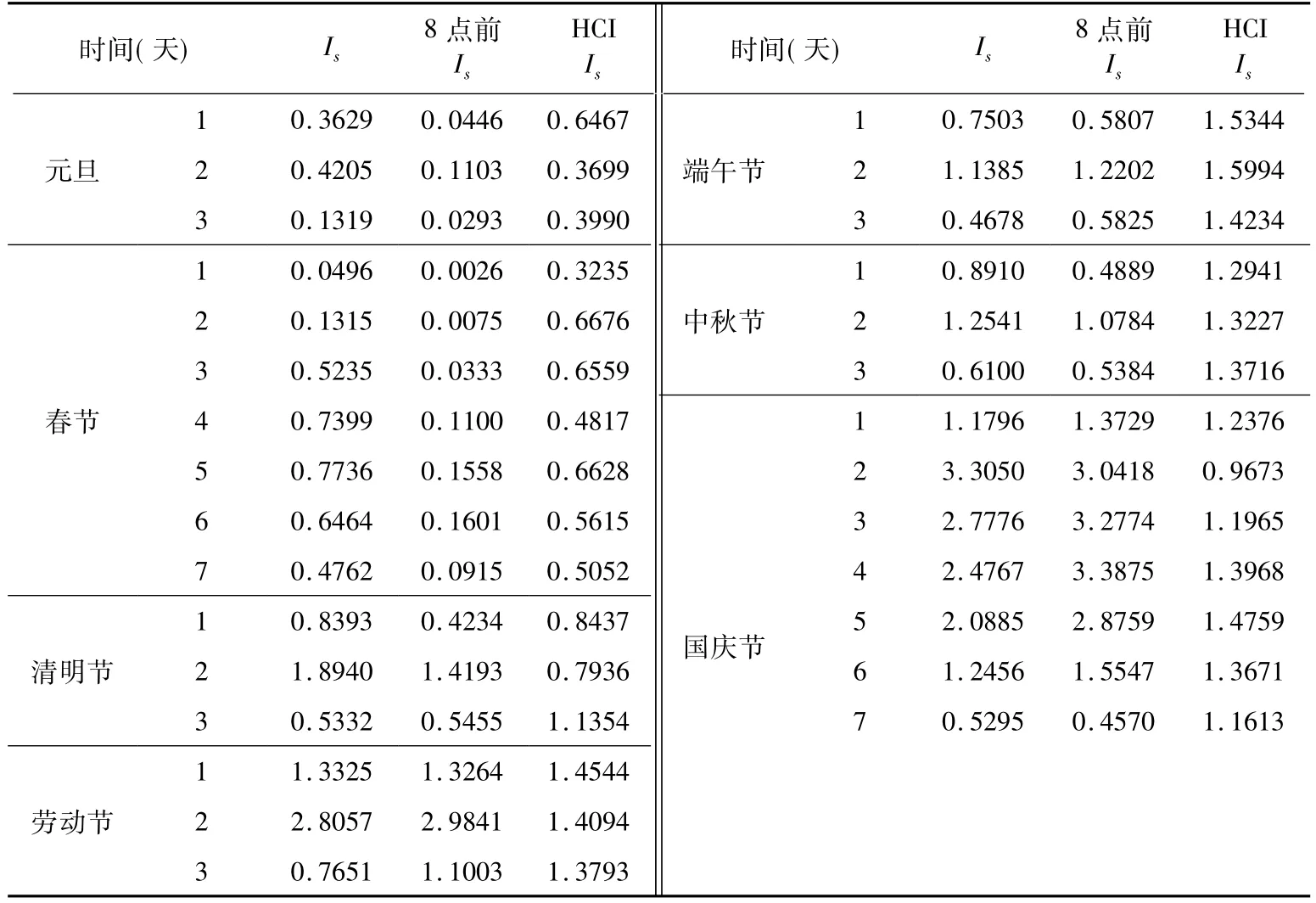
表1 不同节假日季节指数(Is)

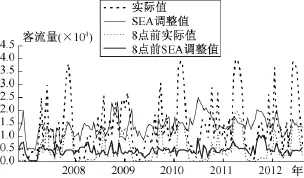
图5 2008～2012年SEA调整后每日客流量、每日8点前客流量

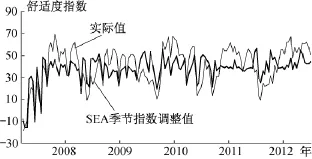
图6 2008～2012年SEA调整后每日人体舒适度指数

2.3 模型参数设置及预测过程

不同节假日休假时间长短对客流量产生明显的影响，为了能够体现出它们在客流量预测中的影响，引入虚拟变量(Kyriakides，Polycarpou，2007)，具体如下:

设季节调整处理后的新数据集为{X'1，X'2，X'3;D1，D2，…，D7}。将新数据集被分为训练集和测试集，其中训练集所选数据为2008～2011年黄山风景区节假日客流量相关数据，样本数目116个;测试集为2012年节假日客流量相关数据，样本数目为29个，同时对数据进行归一化。

表2AGA参数设置

通过Matlab7.0(R2010b)试验平台，输入归一化后的新数据集，定义SVR自由参数初始化种群的粒子，然后对种群数量、进化代数、学习因子、自适应权重进行反复取值测试，最终将AGA各参数设置为如表2所示。同时将交叉验证的折数设为10。经过AGA参数寻优，最终获得SVR模型的最优参数值分别为:C=9.9427，σ2=9.1912，ε=0.0167;CVmse=0.0145%;支持向量个数为47，b=－0.6455。将获得的最优参数值带入SVR模型进行测试，得到模型预测值，将预测值乘以季节调整指数，即为2012年节假日客流量预测值。

2.4 实验结果分析

为了验证基于SEA的AGA-SVR预测的准确性，本文将用AGA-SVR作为对比模型，同时为了证明本文所选取的AGA的有效性，将GA-SVR也作为对比方法。将没有经过季节处理的AGA-SVR预测值、GA-SVR预测值与实际值进行比较，结果如图7、表3所示。为了进一步比较各模型预测结果与实际值的偏差程度，本文使用的评价指标分别为平均绝对误差(Mean Absolute Error，MAE)和均方根误差(Root Mean Square Error，RMSE)(Hong，et al.，2011)、平均绝对百分误差(Mean Absolute Percentage Error，MAPE)和相关系数R(Chen，Wang，2007)(见表4)。

由图7、表3和表4可知:

(1)从图7可以看出，基于SEA的AGA-SVR模型由于在预测之前有效地消除了原始数据的季节成分，使得消除季节成分后的数据更符合SVR预测的要求，且预测之后通过对预测值再次季节调整，使得预测值更接近于实际值，因此预测效果较AGA-SVR、GA-SVR更优。

(2)通过表3可以看出，2012年节假日29天预测值中，基于SEA的AGA-SVR模型预测值最接近实际值的天数为15天，而AGA-SVR为9天，GA-SVR仅为5天，充分说明了本文提出的基于SEA的AGA-SVR模型预测效果优于AGA-SVR、GASVR，尤其体现在每个节假日的人数高峰期如春节(第4、5天)、端午节(第2天)、中秋节(第2天)和国庆节(第2、3天)等，可能的原因在于:在节假日期间，客流量一般呈现出典型的“两头低中间高”季节性趋势，该模型对处理这种季节趋势明显的客流量相对更有效。这对旅游景区有极大的实际意义，因为这些时段游客最多，最容易发生拥堵等突发事件，提前预知客流量，为游客分流、减少门票售出等决策提供重要参考。

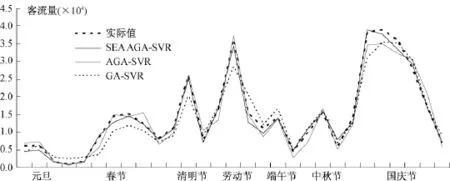
图7 不同模型预测值比较

表3 不同模型预测值比较(归一化后)

表4 不同模型评价指标比较

(3)从预测偏差的角度可以看出(见表4)，基于SEA的AGA-SVR模型MAE、MAPE和RMSE值较AGA-SVR、GA-SVR最小，相关系数R最大，说明基于SEA的AGA-SVR模型预测的值最接近实际值，结果进一步证明了经过季节处理的SVR模型预测效果优于未进行季节处理模型。

(4)同时也可以发现，在3种模型中，基于SEA的AGA-SVR模型预测效果并不总是好于AGA-SVR和GA-SVR，这种情况多出现在节假日的最后1天，如劳动节、端午节、中秋节、国庆节及整个元旦期间，可能的原因在于:在节假日最后1天，客流量将会急剧的回落，这种情况更符合“旅游系统发展天然而稳定的趋势和时间规律”(Faulkner，Russell，1997)，人数波动较小，季节性趋势不明显，此时AGA-SVR和GA-SVR相对来说更有效些，也从另外一个侧面说明了基于SEA的AGA-SVR模型对季节趋势明显的节假日客流量预测的有效性。

(5)在AGA-SVR和GA-SVR比较中，AGA-SVR的总体评价指标较GA-SVR相对来说更有效些，说明了AGA克服了经典GA的无法收敛到全局最优、染色体易丢失和过早收敛等问题，自适应寻优参数能力较GA更有效。

综合以上因素，基于SEA的AGA-SVR模型将季节指数调整、SVR及AGA有效结合，同时处理了节假日客流量预测中的季节性和非线性问题，预测精度最高，是进行节假日客流量预测的有效方法。

3 结论

(1)由于节假日客流量季节性和非线性的双重特征，单纯某一种方法无法准确预测。本文提出了一种基于SEA的AGA-SVR模型，将SEA对季节性的处理、SVR对非线性的预测及AGA对SVR参数的寻优等3种优势结合起来，对节假日客流量进行预测。来自黄山风景区2008～2012年节假日的数据验证结果表明:在和AGA-SVR及GA-SVR等方法比较中，基于SEA的AGA-SVR模型预测精度最高，误差最小，是进行节假日客流量预测的有效方法。

(2)本文提供的节假日客流量预测方法，对旅游景区管理者具有指导意义。节假日是客流量的集中爆发期，准确的预测可为景区管理者在节假日资源统一管理和合理调度、分流游客等方面提供直接信息支持，这对旅游风景区尤其是热门景区乃至整个旅游行业意义重大。该方法同时在相关行业如航空、铁路等交通部门及酒店等行业相关客流量预测中也具有很好的推广应用前景。

除了节假日客流量预测外，旅游业经常会遇到各种突发事件，如自然灾害及突发公共卫生事件等，这种突发事件会对客流量产生极大的冲击，客流量的规律将会打破，因此，突发事件发生后客流量的预测问题将是我们下一步研究和关注的内容。

致谢感谢黄山风景区管理委员会信息中心为本文提供所有相关数据。

［1］杜京义，侯媛彬.基于遗传算法的支持向量回归机参数选取［J］.系统工程与电子技术，2006(9):1430-1433.

［2］Vapnik V N.The Nature of Statistical Learning Theory［M］.许建华，张学工，译.北京:电子工业出版社，2009.

［3］王万良，吴启迪，宋毅.求解作业车间调度问题的改进自适应遗传算法［J］.系统工程理论与实践，2004(2):58-62.

［4］翁钢民，李凌雁.旅游客流量预测:基于季节调整的PSO-SVR模型研究［J］.计算机应用研究，2014(3):692-695.

［5］许光泞，肖志勇，俞金寿.应用自适应遗传算法解决集装箱装载问题［J］.控制与决策，2007(11):1280-1283.

［6］Cai Z J，Lu S，Zhang X B(2009).Tourism demand forecasting by support vector regression and genetic algorithm［C］.Computer Science and Information Technology，IEEE，144-146.

［7］Chen K Y(2011).Combining linear and nonlinear model in forecasting tourism demand［J］.Expert Systems with Applications，38(8)，10368-10376.

［8］Chen K Y，Wang C H(2007).Support vector regression with genetic algorithms in forecasting tourism demand［J］.Tourism Management，28(1):215-226.

［9］Faulkner B，Russell R(1997).Chaos and complexity in tourism:In search of a new perspective［J］.Pacific Tourism Review，1(2):93-102.

［10］Findley D F，Monsell B C，Bell W R，Otto M C，Chen B C(1998).New capabilities and methods of the X-12-ARIMA seasonal-adjustment program［J］.Journal of Business＆Economic Statistics，16(2)，127-152.

［11］Gardner J E S，McKenzie E(1989).Note-Seasonal Exponential Smoothing with Damped Trends［J］.Management Science，35(3)，372-376.

［12］Hong W C，Dong Y，Chen L Y，Wei S Y(2011).SVR with hybrid chaotic genetic algorithms for tourism demand forecasting［J］.Applied Soft Computing，11(2):1881-1890.

［13］Huang J H，Min C H J(2002).Earthquake devastation and recovery in tourism:The Taiwan case［J］.Tourism Management，23(2)，145-154.

［14］Kyriakides E，Polycarpou M(2007).Short Term Electric Load Forecasting:A Tutorial［J］.Trends in Neural Computation，35，391-418.

［15］Nelson C R，Plosser C R(1982).Trends and random walks in macroeconomic time series:some evidence and implications［J］.Journal of monetary economics，10(2)，139-162.

［16］Shiskin J，Young A H，Musgrave J C(1967).The X-11 Variant of the Census Method II Seasonal Adjustment Program［M］.US Department of Commerce，Bureau of the Census.

［17］Song H，Li G(2008).Tourism demand modeling and forecasting—A review of recent research［J］.Tourism Management，29(2)，203-220.

［18］Srinivas M，Patnaik L M(1994).Adaptive probabilities of crossover and mutation in genetic algorithms［J］.Systems，Man and Cybernetics，IEEE Transactions on，24(4)，656-667.

［19］Tseng F M，Yu H C，Tzeng G H(2002).Combining neural network model with seasonal time series ARIMA model［J］.Technological Forecasting and Social Change，69(1)，71-87.

［20］Zhang G P，Qi M(2005).Neural network forecasting for seasonal and trend time series［J］.European journal of operational research，160(2)，501-514.

［21］Zhang H，Wang M，Huang X，Roth H(2014).Application of adaptive genetic algorithm for the parameter selection of support vector regression［J］.International Journal of Modeling，Identification and Control，21(1):29-37.

A Study on the Forecasting Method of AGA-SVR Modeled Holiday Tourist Flows Based on SEA

CHEN Rong1，LIANG Changyong2，GE Lixin3
(1.Department of Economic and Management，Bengbu University，Bengbu，Anhui 233000，China;
2.School of Management，HeFei University of Technology，HeFei 230009，China;
3.Department of science，Bengbu University，Bengbu，Anhui 233000，China)

In virtue of tourists amassing at the same scenic spots in a short term and the different lengths of holidays and seasons，holiday tourist flow is found to present complicated nonlinear features and obvious seasonal characteristics.This paper proposed a forecasting model which combined seasonal exponential adjustment with adaptive genetic algorithm(AGA)and support vector regression(SVR)，and used the new holiday daily data from the famous 5A scenic spot Mount.Huangshan during 2008～2012 to verify its effectiveness.The results indicate that the model，superior to AGA-SVR and GASVR，is an effective way to forecast daily holiday tourist flow.

seasonal exponential adjustment;support vector regression(SVR);adaptive genetic algorithm(AGA);holiday daily tourist flow forecasting

TP 181

A

1006－575(2016)－05－0012－12

(责任编辑:车婷婷)

2015－10－29;

2016－05－18

国家自然科学基金重点项目“基于云的管理信息系统再造研究”(71331002);安徽高校自然科学研究重点项目“智慧景区背景下的旅游客流量预测方法研究”(KJ2015A143);安徽省教育厅2016年高校优秀拔尖人才培育资助项目“高校优秀青年骨干人才国内外访学研修重点项目”(gxfxZD2016283);国家自然科学基金面上项目“基于行为决策的隐性目标决策模型与方法研究”(71271072)。

陈荣(1973－)，女，博士，蚌埠学院经济与管理学院副教授，研究方向为旅游需求预测，E-mail:chenrongustc@163.com。梁昌勇(1965－)，男，博士，合肥工业大学管理学院教授，博导，研究方向为管理信息系统、行为决策及云计算技术等。葛立新(1971－)，男，蚌埠学院理学院副教授，研究方向为数据仿真。