连续刚构桥纵向顶推刚度计算模式比较研究

陈从春， 熊　飞

(上海应用技术学院 城市建设与安全工程学院， 上海　201418)



连续刚构桥纵向顶推刚度计算模式比较研究

陈从春， 熊飞

(上海应用技术学院 城市建设与安全工程学院， 上海201418)

[摘要]连续刚构桥施加跨中合龙顶推力后，墩顶水平位移实测值和理论计算值往往相差很大。比较了群桩基础不同计算模式，并结合实桥施工数据，对合龙顶推力作用下的墩顶水平位移进行了计算分析。研究表明，以双柱刚架模式来模拟群桩基础，从而计算连续刚构桥的纵向抗推刚度，理论计算与实际位移最接近。

[关键词]连续刚构桥； 合龙； 顶推力； 墩顶水平位移； 群桩； 刚度

0前言

预应力混凝土连续刚构桥因其较好的经济性能和使用效果，得到广泛的应用。连续刚构桥是高次超静定结构，在混凝土收缩，徐变及温度作用下次内力较大。为了减小次内力，一般尽量减少主墩纵桥向尺寸，以减少连续刚构桥纵向抗推刚度。连续刚构桥高桥墩也有助于降低抗推刚度，所以连续刚构桥特别适合墩高较高的地方。对于桥址墩高不太高的地方，建造连续刚构桥，为了减少次内力，在中跨合龙时，对梁体施加一个水平顶推力，主墩产生一个反向位移，来抵消温差及后期收缩徐变等因素引起的次内力。连续刚构桥的内力和纵向位移均与桥墩的纵向抗推刚度有很大关系。施工中也发现，合龙顶推时，理论位移与实测位移误差较大，究其原因，是计算模型中抗推刚度差异导致。本文将根据一座实桥的资料及施工情况结合几种不同的计算模式来讨论连续刚构桥的抗推刚度和水平位移计算问题

1纵向抗推刚度计算模式

刚度是指结构抵抗变形的能力。连续刚构桥墩纵向抗推刚度与桥墩群桩基础的约束作用有很大关系。国内外关于桥梁群桩基础计算模式主要有4种[1-8]：即墩底固结模式、比拟杆件模式、双柱刚架模式、桩-土共同作用模式。这4种计算模式中，除第一种墩底固结模式外，其余3种模式都计入了地基土的弹性抗力，这从其公式推导过程中可以看出。

1.1墩底固结模式

墩底固结模式：对承台底部视为固结，其他条件不变，早期的计算采用这一模式[1](见图1)。

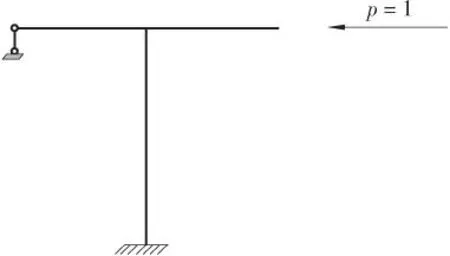
图1　墩底固结模型Figure 1　The pier bottom consolidated model

1.2比拟杆件模式

由于桩基础形式多样，结构受力复杂，影响因素很多，因此一些学者提出一些简化模型的方法，文献[2]提出了比拟杆件模式，文献[3]用另外一种方法验证了比拟杆件模式计算公式，文献[4，5]都采用了这一种方法。该方法将地面线以下的每根桩比拟为一端固结，一端弹性支承的杆件(见图2)，其原理是利用弹性地基梁的幂级数法得到桩基在冲刷线下的柔度计算公式，然后构成桩顶系数柔度矩阵，通过求其逆矩阵得到桩顶刚度矩阵，然后与杆端刚度矩阵组合，组合时在桩顶增加抗推弹簧，从而得到等代杆件的抗推刚度。这种方法比拟前后的桩数不变，桩的布置不变。此法可以精确的模拟地面线(冲刷线)以下的桩基作用。

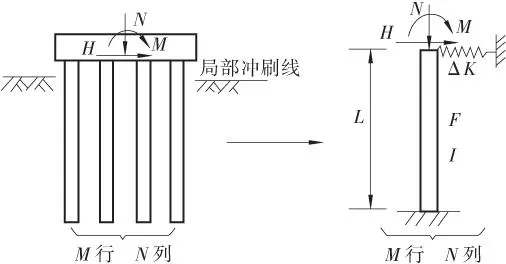
图2　比拟杆件模型Figure 2　The bar simulation model

等代结构参数计算公式由变位互等定理可得δQM=δMQ，以下公式均由δQM代替表示：

水平弹簧刚度和等代单根桩基面积：

等代单根桩长和等代单根桩截面惯性矩：

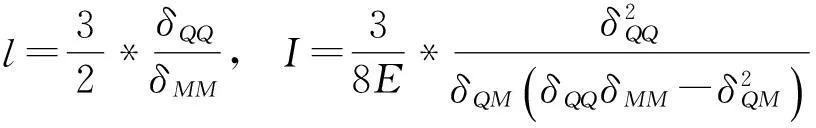
式中：

δQQ：桩顶作用单位横轴向力时在桩顶产生的横轴向位移；

δQM：桩顶作用单位横轴向力时在桩顶产生的转角；

δMQ：桩顶作用单位弯矩时在桩顶产生的横轴向位移；

δMM：桩顶作用单位弯矩时在桩顶产生的转角。

1.3双柱刚架模式

文献[6]提出了双柱刚架模式，他以两者柔度相同为基础，利用等效模拟的方法将实际的桩基础模拟成双柱刚架式基础模型(见图3)。

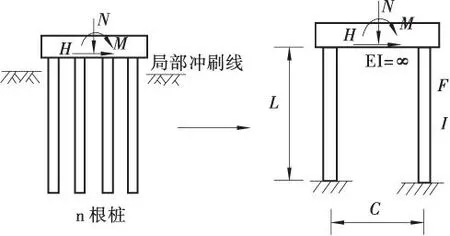
图3　双柱刚架模型Figure 3　The double column frame model

计算承台底面柔度系数(原结构在单位荷载作用下)：

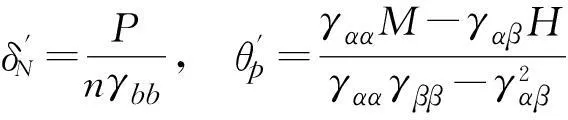
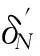
双柱框架的四个待定参数分别为：

等代桩长和等代桩基惯性矩：

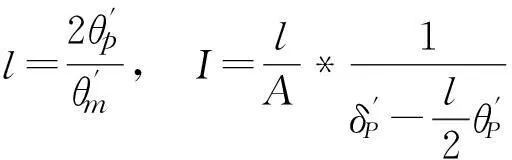
等代桩基截面积和等代结构桩距：

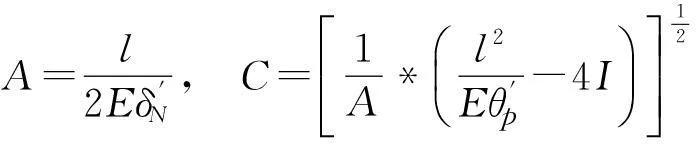
1.4桩-土共同作用模式[1]

考虑桩侧土体对桩基的弹性抗力，用土弹簧模拟土体。土弹簧刚度k表征土体抗力：k=m*z*bf*Δz其中：m：地基土比例系数；z：各土层中点到地面的距离；bf：桩基的计算宽度；Δz：各土层的厚度。

桩土共同作用模式中，土弹簧的刚度k对结构纵向刚度影响较大，而土弹簧的刚度k主要由地基土比例系数m确定，m值根据桩侧土质按测试值采用，如无实测数据按文献[9]采用。对桩土共同作用模式，根据桩底是嵌岩桩或摩擦桩，分为桩底固结(见图4)或桩底采用节点弹性支承连接(见图5)。桩底弹性支承的刚度与桩底土质的竖向比例系数有关，如无实测数据按文献[9]采用。

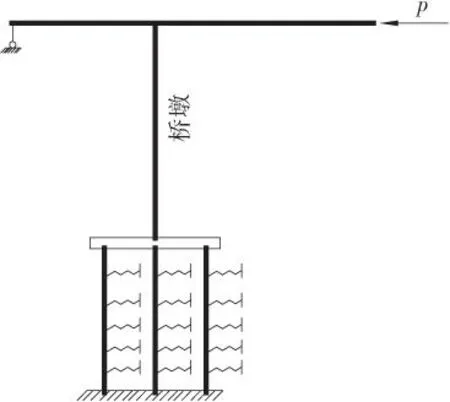
图4　带侧向弹簧的桩底固结模型Figure 4　The model of pier with consolidated bottom 　and lateral spring

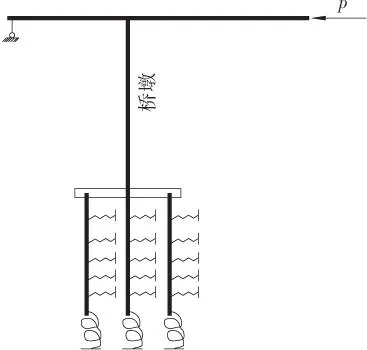
图5　桩底弹性支承模型Figure 5　The model of pier with bottom and lateral spring

2工程背景

鸡啼门特大桥主桥处于珠海市，南岸处于小林镇内、北岸处于乾务镇内。鸡啼门特大桥主桥桩号为K17+890～K18+242，全长352 m。主桥上部结构：(96 m+160 m+96 m)三跨连续刚构箱梁，共分为27个梁段，其中0#梁段为立托架现浇，1～19#梁段采用挂篮悬臂现浇施工，20#梁段为合龙段，21#～26#梁段为边跨现浇段(采用支架施工)。悬浇段长3.0～4.5 m。纵向采用变高度，主梁处梁高9 m，边墩处梁高3.5 m，跨中梁高3.5 m。 半幅桥宽12.75 m，采用单箱单室箱形断面，其中箱宽6.5 m，两侧翼缘板悬臂长3.125 m。两幅桥结构间距0.5 m。

主梁采用三向预应力体系。下部结构：主桥桥墩采用双肢薄壁墩，单肢采用实心截面，纵桥向厚1.8 m，横桥向与上部箱梁箱宽相同为6.5 m，半幅桥主墩基础采用9 根D180 cm 钻孔灌注桩，采用嵌岩桩。边墩同样采用方墩断面，墩身截面为2.0×2.0 m，半幅桥2 根，半幅桥基础采用4 根D180 。承台采用工字形截面，纵桥向宽为8.0 m，横桥向宽9.5 m，厚为2.8 m。施工合龙工序采用先边跨后中跨的合龙顺序。

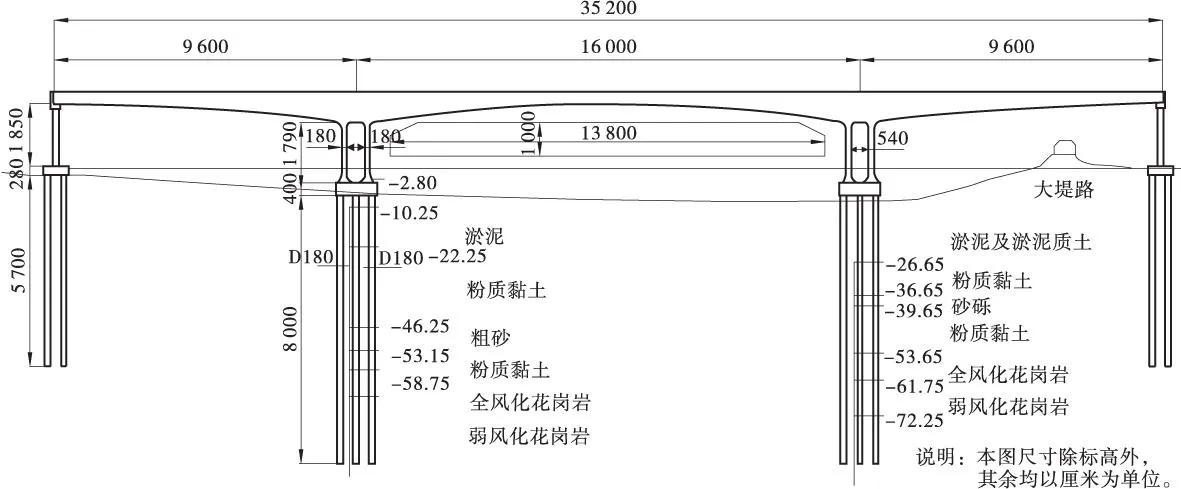
图6　鸡啼门特大桥立面图Figure 6　Elevation view of Ji Timen bridge

地质情况：根据钻孔揭示及工程地质调绘，桥区地层至上而下依次为 ①人工堆积层(Q4me)，厚度为0.50～2.00 m。 ②第四系海相沉积层(Qmc)，厚度3.00～22.50 m。 ③第四系全新统残积层(Qel)，厚度1.40～23.40 m。 ④燕山三期的第二次侵入岩体-粗粒花岗岩(ηΥ52-3a)，厚度一般大于50 m。鸡啼门大桥主桥立面图(见图6)。设计图纸上提出中跨合龙时施加300 kN的顶推力，主墩往河外侧偏移33.2 mm，如果实际施工时，与实测位移相差±5%，则查找原因。而实际按300 kN顶推后，墩顶位移只有8 mm[10]，理论墩顶位移与实际差别已经远远超过了±5%，相差特别大。

3计算参数及有限元模型建立

对于墩梁固接的连续刚构体系，特别是变截面箱梁，由于合龙温差和混凝土的收缩，徐变，从而产生结构内力重分布和变位的非线性，依靠手算很难得到精确解，因此本文采用大型专用桥梁有限元计算软件—Midas civil，按照施工顺序建立有限元计算模型。

主梁采用C55混凝土，比重用26 kN/m3，弹性模量采用3.55×104MPa，混凝土收缩徐变特性全部按照规范规定取值。预应力采用钢绞线束施加，钢绞线弹性模量采用1.95×105MPa，钢绞线采用ASTM标准，标准抗拉强度1 860 MPa，张拉控制应力采用1 395 MPa。主梁划分为118个单元，4个桥墩划分为64个单元，2个承台划分为16个单元，18根桩基划分为360个单元。

鸡啼门大桥有限元模型(见图7)。

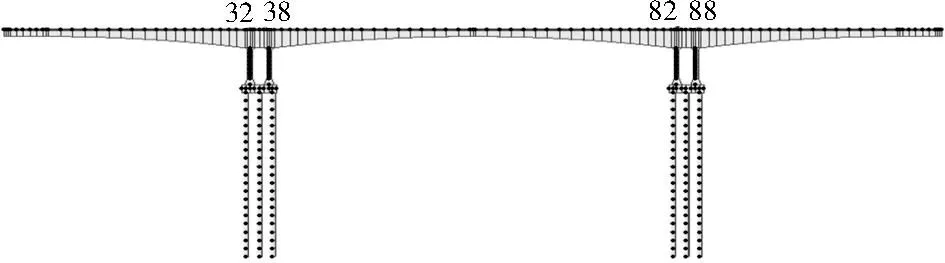
图7　有限元计算模型Figure 7　The finite element model

44种计算模式分析比较

4.1墩底固结模式

用墩底固结法计算墩顶位移值见表1，其墩顶平均位移为4.524 mm。

4.2比拟杆件模式

根据鸡啼门实桥资料，计算得到桩基在局部冲刷线处柔度系数值为(m值取5 000 kN/m4)：

δQQ=0.136×10-4m，δQM=0.021 7×10-4rad，

δMM=0.005 61×10-4rad。

计算得等代结构参数：

ΔK=3.4×104kN/m，A′=1.91 m2，l=36.36 m，I=0.35 m4。

利用这些参数建立midas有限元模型，计算出墩顶位移值(见表1)：

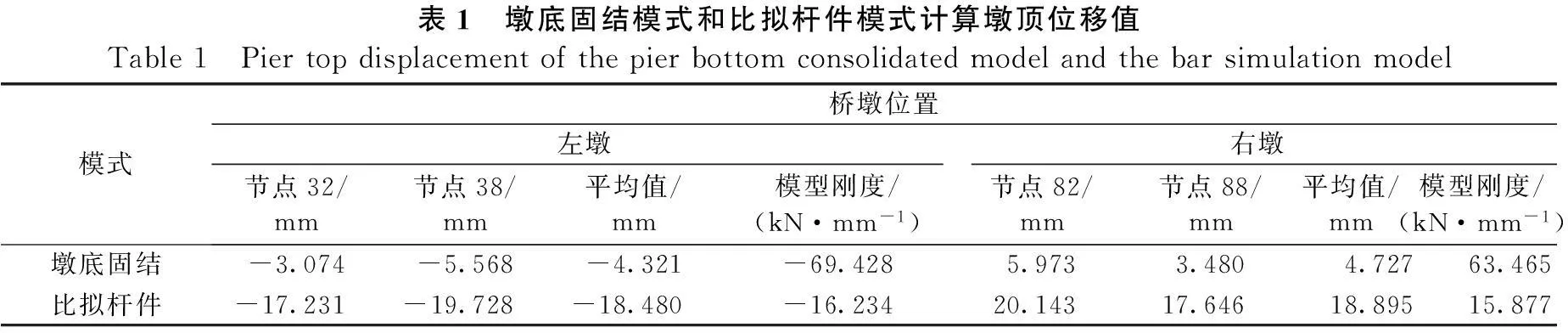
表1 墩底固结模式和比拟杆件模式计算墩顶位移值Table1 Piertopdisplacementofthepierbottomconsolidatedmodelandthebarsimulationmodel模式桥墩位置左墩右墩节点32/mm节点38/mm平均值/mm模型刚度/(kN·mm-1)节点82/mm节点88/mm平均值/mm模型刚度/(kN·mm-1)墩底固结-3.074-5.568-4.321-69.4285.9733.4804.72763.465比拟杆件-17.231-19.728-18.480-16.23420.14317.64618.89515.877

该方法的平均位移为18.688 mm。

4.3双柱刚架模式

根据鸡啼门实桥资料，计算得到承台底面柔度系数值为(m值取5 000 kN/m4)：

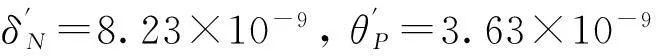
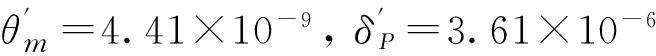
计算得等代结构参数：

l=1.65 m，A=3.18 m2，I=1.65×10-3m4，

C=2.74 m。

利用这些参数修改上述midas模型的桩基础，计算出墩顶位移值(见表2)：

用该方法计算所得的平均位移为11.264 mm。

表2 双柱刚架模式计算墩顶位移值Table2 Piertopdisplacementofthedouble-columnrigidframemodel模式桥墩位置左墩右墩节点32/mm节点38/mm平均值/mm模型刚度/(kN·mm-1)节点82/mm节点88/mm平均值/mm模型刚度/(kN·mm-1)双柱刚架-9.803-12.309-11.056-27.13512.72310.21811.47126.153

4.4桩-土共同作用模式

根据鸡啼门有限元模型，计算各墩顶位移值(见表3)

根据上面三种约定条件所算得位移值的比选，m取最小值的平均位移为14.496 mm，m取最大值的平均位移为13.628 mm。桩底竖向节点弹性支撑的平均位移为14.000 mm，桩底固结约束的平均位移为13.987 mm。

表3 桩-土共同作用模式计算墩顶位移值Table3 Piertopdisplacementofthepile-soilinteractionmodel桥墩位置左墩右墩节点32/mm节点38/mm平均值/mm模型刚度/(kN·mm-1)节点82/mm节点88/mm平均值/mm模型刚度/(kN·mm-1)m取最小值-13.047-15.548-14.298-20.98215.94313.44314.69320.418m取最大值-12.180-14.680-13.430-22.33815.07512.57613.82621.698桩底竖向节点弹性支撑-12.552-15.052-13.802-21.73615.44712.94814.19821.130桩底固结约束-12.539-15.039-13.789-21.75615.43412.93514.18521.150 注:关于桩基各土层对应M取值,kN/m4:淤泥(0～24m):3000～5000;粉质粘土(24～44m):6000～10000;粗砂(44～60m):20000～30000;碎石(60～76m):30000～80000,花岗岩(76～80m):300000。桩底弹性支承和桩底固结其m值取中值。

5结论

在对连续刚构梁桥进行建模分析时，根据相同的顶推力，不同的边界的条件，会得出不同的位移值，因此确定合理的边界约束条件，建立与实际接近的模型是很有必要的。

综合国内外情况，群桩基础连续刚构桥纵向顶推计算模式可分为墩底(承台)固结模式、比拟杆件模式、双柱框架模式、桩-土共同作用模式这四张模式。

以鸡啼门大桥为背景，比较了在300 kN水平合龙推力时，4种计算模式有限元结果和实测值，表明双柱刚架模式更接近实际结果，但需要更多的实际工程来验证。结果可作为其他类似工程参考。

[参考文献]

[1]范立础.桥梁抗震 [M].上海：同济大学出版社，1998.

[2]万科峰.桥梁结构分析中桩基的简化方法-桩基等代法[J].中南公路工程，1990，54(3)：54-58.

[3]程翔云.群桩基础等代模型的改善[J].公路，2006(01)：13-16.

[4]王文涛.刚构-连续组合梁[M].北京：人民交通出版社，1997.

[5]邬晓光.刚架桥[M].北京：人民交通出版社，2002.

[6]鲍卫刚.桥梁承台桩基柔度的模拟[J].华东公路，1992，78(5)：16-17.

[7]袁洪.桩基结构模拟法[J].公路，2000(04)：7-12.

[8]Mohamed Ashour，M.ASCE，and Hamed Ardalan.Employment of the P-Multiplier in Pile-Group Analysis[J].American Society of civil Engineers，2011，16(5)：612-623.

[9]JTG D63-2007，公路桥涵地基与基础设计规范[S].

[10]陈从春.珠海机场高速鸡啼门特大桥主桥施工监控报告[R].上海，2012.

The Comparative Study of Continuous Rigid Frame Bridge Longitudinal Incremental Launching Stiffness

CHEN Congchun， XIONG Fei

(School of Urban Construction and Safety Engineering， Shanghai Institute of Technology， Shanghai 201418，China)

[Abstract]There are much difference between the measured horizontal displacement and theoretical value of the pier top when the continuous rigid frame bridge jacked by horizontal closure force.The pile group foundation theoretic models are compared and the horizontal displacement of pier top is calculated under the practical bridge construction.The research proved that the double-column-frame-model theoretical value is more closed to that of measured.

[Key words]continuous rigid-frame bridge； closure； jacking force； horizontal displacement at pier top； pile group； rigidity

[中图分类号]U 448.23

[文献标识码]A

[文章编号]1674-0610(2016)01-0163-04

[作者简介]陈从春(1970-)，男，湖北公安人，博士，副教授，从事桥梁工程教学与研究工作。

[基金项目]上海应用技术学院科研项目(10110L140007)

[收稿日期]2015-11-19