基于ANSYS的弧齿锥齿轮动力学模态分析

刘迎娟，韩彦龙，王　彬，李少杰

(1.华北理工大学 迁安学院，河北　迁安　064400；2.承德石油高等专科学校 机械工程系，河北　承德　067000；3.承德石油高等专科学校 汽车工程系，河北　承德　067000)



基于ANSYS的弧齿锥齿轮动力学模态分析

刘迎娟1，韩彦龙2，王彬1，李少杰3

(1.华北理工大学 迁安学院，河北迁安064400；2.承德石油高等专科学校 机械工程系，河北承德067000；3.承德石油高等专科学校 汽车工程系，河北承德067000)

摘要：以某弧齿锥齿轮为研究对象，运用三维建模软件Pro/E进行参数化建模，并将模型导入有限元软件ANSYS中进行动力学模态分析，得到齿轮在高速运转时的模态特性。研究表明：考虑转度的影响时，齿轮高速旋转下会发生离心刚化效应，并产生预应力；预应力导致弧齿锥齿轮的固有频率和主阵型发生了显著改变。该研究为弧齿锥齿轮的模态研究提供了理论支持和重要参考。

关键词：弧齿锥齿轮；ANSYS；动力学；模态分析

弧齿锥齿轮作为飞机、船舶、精密机床、工程机械和汽车中广泛使用的传动部件，常处于高速旋转或者重载等恶劣工作状态下，因此只通过对齿轮进行限制自由度的常规模态分析，不能满足实际应用的需求[1-3]。鉴于此，本文考虑了转速对齿轮模态特性的影响，通过有限元分析得到其前六阶的固有频率和主阵型，该研究对齿轮的设计具有实际的指导性作用。

1弧齿锥齿轮有限元模型

1.1三维参数化建模

根据齿轮啮合原理，紧密联系其实际切齿过程，通过一系列数学推导，得到了弧齿锥齿轮的球面渐开线方程，然后利用Pro/E建立了其精确的三维参数化基础模型[4]。本文以一对相互啮合的齿轮中的小齿轮为例，通过在基础模型上输入相关参数，即可得到齿轮精确三维模型，齿轮参数设置如表1所示。

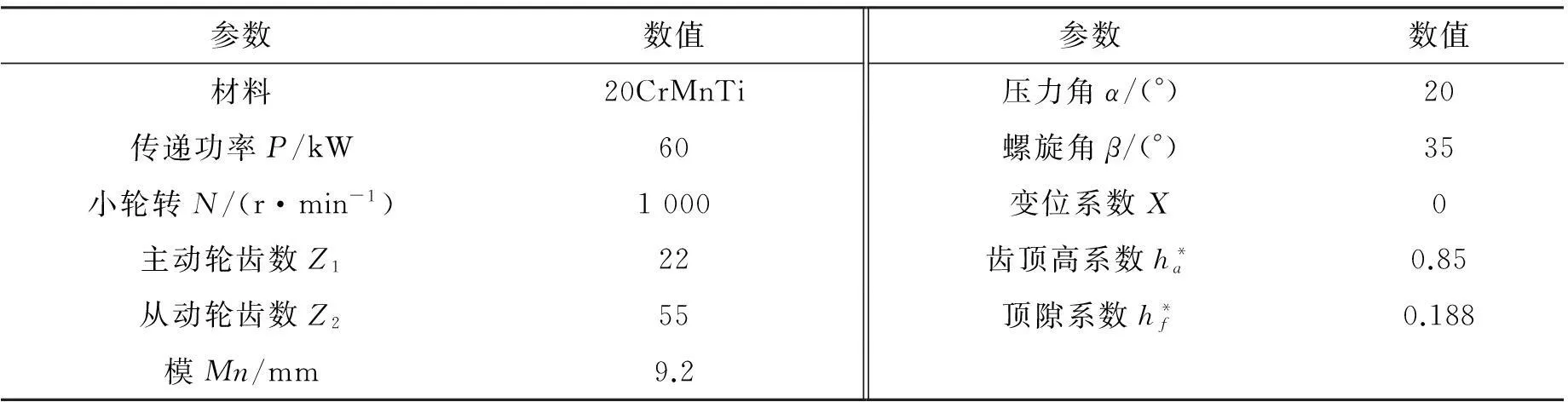
表1　弧齿锥齿轮参数表

1.2有限元分析边界条件

将Pro/E软件创建好的弧齿锥齿轮三维模型保存为.x_t格式文件并导入ANSYS软件中，设置文件名字后进入前处理器，设置单元类型、材料属性等。本研究的齿轮材料为20CrMnTi，通过查阅机械设计手册可得弹性模量为2.07×105MPa，泊松比为0.25，密度为7.86×10-6kg/mm3。由齿轮安装条件可知，约束条件为：轴向和周向固定，径向自由。

1.3有限元模型

研究选择具有八节点、六面体结构的Solid 45单元，相关命令流如下：

/prep7(进入前处理模块)

ET,1,Solid45,,1(定义单元类型)

MP,EX,1,2.07E11(定义弹性模量)

MP,PRXY,1,0.25(定义泊松比)

MP,DENS,1,7800(定义材料密度)

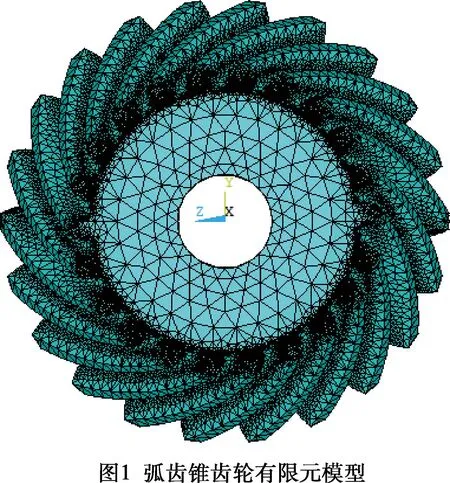
模态分析是对整个齿轮进行的分析，故网格划分时采用mesh tool中的智能网格划分即可满足求解要求，划分等级默认，划分结果如图1所示。

2静力分析

在进行高速旋转状态下的模态分析前，需首先对模型进行静力分析，划分完网格后对齿轮进行加载，在静止状态下齿轮的边界条件是限制轴孔内圈所有节点的全部自由度。加载完成后设置模型求解的类型为Modal，选择分块Lanczos法对模型进行求解，设置提取前六阶的固有频率和振型。求解完成后，进入后处理器可提取固有频率及其变形量。

3动力学模态分析

3.1约束条件

将模型导入ANSYS后，与上一节设置相同，进行前处理工作，另设置齿轮的转速。由于网格划分是采用智能划分的方法，网格质量较低，为节省计算时间也使运算更顺利地进行，应将临近范围内的节点合并。另外在定义边界条件时，考虑模型的旋转情况，须将直角坐标系转化为柱坐标系，然后再进行定义。由ANSYS软件中局部坐标坐标系的建立规则可知，柱坐标系的Z轴应与齿轮的旋转轴重合，X轴表示径向方向，Y轴表示转角方向。设置完成后进行求解。

3.2动力学模态分析

前文的静力分析结果作为动力学模态分析的预应力，设置如下命令流：

/solu

alls

antype,modal(模态分析)

modopt,subsp,10(选择模态分析方法，子空间法)

mxpand,10

alls

pstres,on(将静力分析结果作为模态分析的预应力)

OMEGA,zhuansu/60,,,1

3.3模态分析结果

为更好地揭示弧齿锥齿轮的模态特性，本文选取了大齿轮在转速分别为2 000、4 000 、6 000、10 000 r/min 的工作状态为例，提取了前六阶固有频率，整理如表2所示。

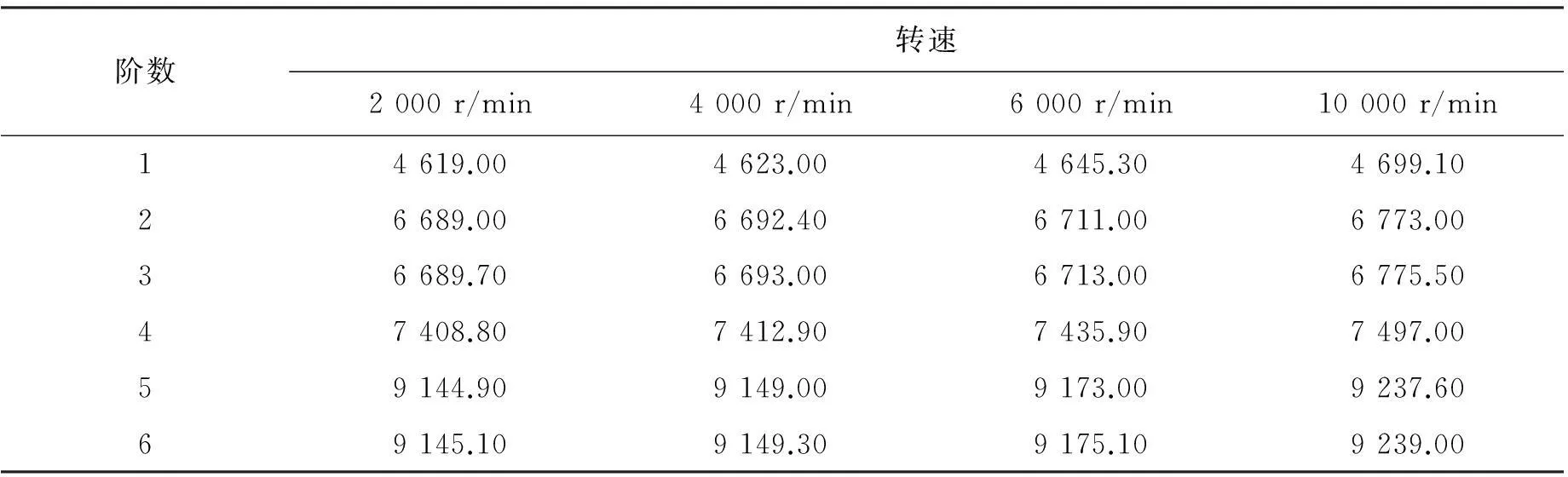
表2　不同转速下主动轮前六阶固有频率　Hz

3.4阵型结果分析

由于篇幅限制，本文以转速10 000r/min时的第四阶阵型图(图2)为例，并对比分析齿轮在不同转速下，以分度圆为度量值，沿齿宽方向从小端到大端的位移变化量，整理结果后得到图3。

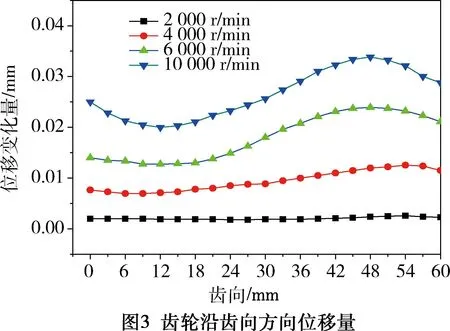
由图2和图3可知，随着齿轮转速的提高，其相同部位的位移改变量也会随之增大，但是由于弧齿锥齿轮模型的几何形状复杂，且螺旋趋势明显，所以齿轮的变形量并不是呈随速度的升高而规律性的上升状态，而是在齿轮的大、小两端表现为波动的状态。

4结语

本文以某弧齿锥齿轮为研究对象，通过分析对其在不同转速下模态特性进行分析，得出如下结论。

1)齿轮转速的施加会产生径向离心力，使得齿轮各阶固有频率升高，随着转速的升高，各阶固有频率有逐步升高的趋势。2)“离心刚化效应”是导致齿轮内部结构发生变化进而引起模态特性变化的原因，高速运转时轮齿部分在周向出现扭转变形，沿径向方向发生了扩张。3)模态特性分析可以很好地判断零部件的自身特性，为模型设计、结构优化及高效使用提供重要依据。

参考文献：

[1]慕灿，陈科.葛林森弧齿锥齿轮的有限元模态分析[J].佳木斯大学学报(自然科学版),2013(5):704-707.

[2]韩彦龙.空分压缩机多机组轴系模态分析[J].承德石油高等专科学校学报,2015(1):21-24.

[3]李杰，项昌乐.高速旋转状态下的齿轮非线性模态分析[J].现代制造工程, 2007(7):77-79.

[4]孙伏.基于ANSYS的少齿数齿轮模态分析与研究[J].机械设计与制造,2011(5):119-121.

[5]刘迎娟，冯立艳.弧齿锥齿轮的有限元分析[J].河北联合大学学报(自然科学版),2014,36(1):32-35.

Dynamic Modal Analysis of Spiral Bevel Gears Based on ANSYS

LIU Ying-juan1, HAN Yan-long2, WANG Bin1, LI Shao-jie3

(1.Qian’an North China University of Science and Technology, Tangshan 064400, Hebei, China;2.Department of Mechanical Engineering, Chengde Petroleum College, Chengde 067000, Hebei, China;3.Department of Automotive Engineering, Chengde Petroleum College, Chengde 067000, Hebei, China)

Abstract:Taking gear as the research object, the paper achieves its parametric model with 3D software Pro/E. Also, the model is imported into the ANSYS for dynamic modal analysis and the modality characteristic of gears under the high speed environment is got. The study shows that considering the effect of speed, the centrifugal effect of players of the gear will occur and then will produce prestress with the high-speed rotating, which will lead to the change pattern of the gear modal characteristics.

Key words:spiral bevel gears; ANSYS; dynamics; modal analysis

中图分类号：TH132.4

文献标识码：A

文章编号：1008-9446(2016)01-0025-04

作者简介：刘迎娟(1986-)，女，河北保定人，华北理工大学迁安学院助教，硕士，主要研究方向为机构学与机械动力学。

收稿日期：2015-10-09