水平荷载下海上风机单桩基础桩土相互作用研究*
刘红军, 尹燕京, 常季青
(1.海洋环境与生态教育部重点实验室, 山东 青岛 266100; 2. 中国海洋大学环境科学与工程学院, 山东 青岛 266100;
3.青岛市勘察测绘研究院, 山东 青岛 266032)
水平荷载下海上风机单桩基础桩土相互作用研究*
刘红军1, 尹燕京2, 常季青3
(1.海洋环境与生态教育部重点实验室, 山东 青岛 266100; 2. 中国海洋大学环境科学与工程学院, 山东 青岛 266100;
3.青岛市勘察测绘研究院, 山东 青岛 266032)
摘要:海上风电作为一种清洁绿色的能源越来越受到人们的关注,海上风机会承受风、浪、流等水平荷载的作用,因此水平荷载下海上风机单桩基础桩土相互作用一直是人们研究的热点。本文对水平荷载作用下海上风机单桩基土相互作用进行研究,通过ABAQUS有限元数值分析软件建立桩土模型。结果显示:桩顶水平极限位移约为11.25 cm,海床面以下1~5 m范围为桩身弯矩和桩身mises应力较大的区段;随着桩顶水平位移的逐渐增大,桩身挠曲逐渐向深处发展,桩体位移零点位置逐渐向下;桩体的水平位移会对桩侧土体产生挤压作用,这种挤压作用会使土体塑性屈服区逐渐向下发展,土体水平位移呈半圆形放射状分布,浅层土体mises 应力产生非对称分布。
关键词:海上风机; 单桩基础; ABAQUS; 水平荷载; 桩土相互作用
LIU Hong-Jun, YIN Yan-Jing, CHANG Ji-Qing. Research on the Pile-Soil Interaction of Monopile Foundation Under Horizontal Load for Offshore Wind Turbine [J]. Periodical of Ocean University of China, 2016, 46(3): 113-120.
海上风电是一种清洁的绿色能源,而且储量丰富,据统计,海上风电储量约为7.5亿kW。海上风电与陆上发电相比具有建设周期短、运营成本低的优点,因此全世界很多国家都在大力建设海上风电场[1]。近些年来,中国也逐步投入大量资金发展海上风电。位于山东半岛的黄河三角洲地区具有得天独厚的自然条件,地势平坦无阻碍,风力密度均匀,是发展海上风电的极佳地区[2]。
目前海上风机的基础形势有多种,其中单桩基础占了相当大的比例,单桩基础具有结构简单、安装迅速的优点,具有很大的开发利用前景。目前对于水平荷载作用下桩土相互作用的研究主要有m法、p-y曲线法、有限单元法等,其中m法是一种线弹性地基反力法,主要适用于桩侧土体处于弹性变形阶段范围内的求解,其计算结果往往和实际情况有一定差距。p-y曲线法是一种弹塑性地基反力法,可以适用于计算大变位时桩身受力状态,不仅能够考虑静荷载,还能考虑循环荷载、土的软化、土抗力折减等,有效地克服了m法的缺陷。Matlock[3]最早提出了软黏土的p-y曲线、Reese[4]、O’Neill[5]分别提出了硬粘土和砂土的p-y曲线,三种经典p-y曲线已经被列入美国石油协会规范[6]。有限单元法的核心是将复杂的研究对象离散为一个个微小的单元,根据最小势能原理来求解刚度矩阵方程。有限元法具有适用于解决非线性非均质问题并能模拟材料复杂的本构关系的优点。刘冰雪等[1]通过建立三维有限元模型,重点研究了桩径、桩长等因素对桩基水平及竖直承载性能的影响。Abdel-Rahman等[7]重点关注了波浪荷载下桩基水平变形特征,并将计算结果与p-y曲线法做了对比,发现p-y曲线法得到的研究结果偏于保守。以往有限元法应用于海上风电桩基的研究中,往往注重于单桩基础本身的水平承载能力,而对桩土相互作用研究相对较少。在实际情况中海上风电桩基的水平失稳往往不是桩基自身的破坏,而是桩侧土体的破坏,因此桩土相互作用研究是桩基水平承载性能的研究核心。针对这一问题,本文以黄河三角洲地区工程地质条件为背景,利用大型有限元分析软件ABAQUS研究了水平荷载作用下海上风机单桩基础桩土相互作用,对桩基水平极限承载力、桩身内力和变形以及土体变形等进行了深入分析,研究成果可以为海上风电场建设提供一定参考。
1有限元模型
有限元模型建立的正确与否直接影响分析结果的准确性和可靠性,模型以黄河三角洲地区为背景,以下将从模型部件及物理参数、分析步设置、 网格剖分以及模型验证4个方面介绍有限元模型。
1.1 模型部件及物理参数
模型桩采用钢管桩,模型在桩土之间留出50mm的空隙做混凝土灌浆处理,土层厚度一般取桩入土深度的1.25倍,模型取H=20m,土体半径约为桩半径的36倍,可以忽略边界效应的影响,模型参数见表1。

表1 部件及物理参数
1.2 分析步设置
模型水平加载采用位移控制法,部件全部采用浮重度进行计算,在模型中规定全局直角坐标系z轴正方向为重力方向,荷载位移沿y轴施加,数值以y轴正方向为正值。在实际状况中,假定海床泥面处位移为零,土体内部是有应力存在的,因此在施加水平荷载前必须进行初始地应力平衡。但是知道土体内部应力的真实数值是很困难的,为此采取的方法为:施加水平荷载前,将桩、混凝土灌浆材料的密度设置为与土体一致,对整个模型施加重力荷载,得到的土体内部应力作为初始条件写入模型中,再施加重力以平衡,然后对桩和混凝土材料设置施加体力荷载分析步以弥补密度差异。经验算,这种方法计算出来的初始地应力与实际状况基本一致。
关于桩土间接触分析,为解决由于接触状态剧烈改变而导致求解过程不收敛问题,模型专门设置静力分析步使接触关系平稳建立起来,这样不仅解决了收敛问题,还提高了求解效率。
1.3 网格剖分
在ABAQUS中,网格划分方式与网格疏密程度对分析结果的准确性影响重大。由于本模型涉及桩和土体的扭曲变形以及桩土间接触分析,因此采用8节点6面体线性缩减积分三维实体单元(C3D8R),此类单元相比于其他单元更适用于接触分析,对位移求解精度更高而且单元扭曲变形时不会产生剪切自锁问题。网格划分后的模型见图1。

图1 网格剖分示意图
1.4 模型验证
为验证模型的合理性,本文采用文献[8]中试验实测粉土p-y曲线,根据桩的挠曲方程采用有限差分方法求解桩身弯矩和位移,并与本模型有限元计算结果进行对比,得到100kN水平荷载作用下桩身弯矩位移分布对比图(见图2)。

图2 有限元计算桩身弯矩位移与p-y曲线法结果比较
图2表明有限元解与p-y曲线解基本一致,因此可以认为本模型是合理可靠的。
2计算结果分析
2.1 桩基水平极限承载力分析
桩基础的水平极限承载力,可用p-s曲线法来确定[11]。为了简化计算和大致模拟桩顶风机所受到的风荷载等水平荷载,通过控制桩顶位移来实现加载,然后根据模型输出的桩顶反力得到桩基水平荷载-位移曲线。达到极限荷载时桩基水平位移往往已经超过了顶部建筑物的容许位移,此时通过借鉴等效塑性应变(PEEQ)云图来辅助判断基础是否达到了极限荷载破坏状态。有限元计算模型桩基础p-s曲线见图3。
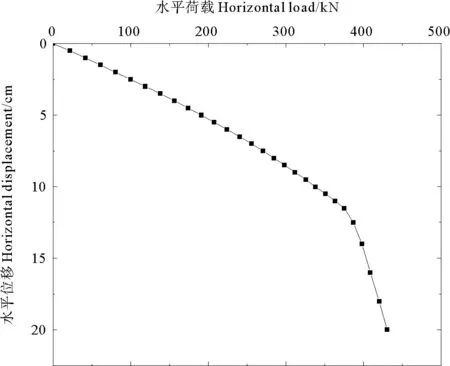
图3 桩基p-s曲线
图3表明当桩顶水平位移为11.25cm时,桩基p-s曲线出现明显拐点,此位置对应的桩顶水平荷载即为单桩基础水平极限承载力,即P=375.22kN。等效塑性应变大于零即代表土体已经屈服,结合此时的等效塑性应变云图(见图4)可以判断单桩基础底部土体形成半圆形破坏区域,但并未贯通至土底;浅层与桩体接触的土体也产生了较大的剪切破坏,破坏深度约为6.2m,从而导致桩体背向施力一侧与土体分离,泥面处的水平分离长度约为4.19cm。

图4 水平极限荷载作用下有限元模型等效塑性应变云图
2.2 桩体内力分析
在ABAQUS中,无法直接在CAE模型中设置输出桩身弯矩,但是通过在模型inp文件中写入 “define cutting surface”与“section print”命令即可解决这一问题。由2.1已知桩基达到水平极限承载力时对应的桩顶水平位移为11.25cm,因此采用位移控制法,设置桩顶水平位移u分别为1、3、5、7、9和11.25cm的6个分析步(具体分析步设置见表2),每个分析步均输出桩身弯矩,得到桩身弯矩分布如图5所示。

表2 分析步设置

图5 不同桩顶位移下桩身弯矩分布
规定海床面处z坐标为0,图5表明桩身弯矩随着桩顶水平位移的增大而增大,桩顶位移越大,代表有限元计算模型施加在桩顶的水平荷载越大。每一级加载桩身弯矩最大值出现在海床面以下3m左右,达到极限承载力时,桩身最大弯矩约为2217kN·m。随着桩顶水平位移的不断增大,桩身最大弯矩基本呈线性增长,即桩顶水平位移每增加1cm,桩身最大弯矩增大约为212kN·m。在同一桩顶水平位移条件下,桩身弯矩由桩顶开始向下逐渐增大,达到最大弯矩位置后随深度增加而减小。
在材料力学中,mises应力是根据第四强度理论得到的一种等效应力,常用来描绘联合作用下复杂应力状态,是衡量应力水平的主要指标。其计算公式为:

其中:σzs为mises应力;σ1、σ2、σ3分别为第一、二、三主应力。桩身mises应力云图(见图6)表明:随着桩顶水平位移的不断增大,挤压土体一侧的桩身应力以海床面以下3m深度为中心向桩基两端不断发展增大,桩顶到达极限水平位移时,桩身最大应力为56MPa。桩顶和桩底应力较小,最小应力出现在桩最上端,约为5.77MPa。

图6 不同桩顶位移下桩身mises应力云图对比
在ABAQUS visualization(可视化后处理)模块中提供了多种显示分析结果的方式,其中通过定义节点路径,可以很方便的显示沿路径mises应力的变化。因此,为了进一步研究桩身mises应力的变化,在ABAQUS后处理中建立桩体挤压土体一侧由桩顶至桩底的竖直方向节点路径,得到不同桩顶位移下沿路径的mises应力变化对比图(见图7)。综合图6、7表明,桩身最大应力出现在海床面以下3m左右,与桩身最大弯矩位置相同,并随着桩顶位移的增大而迅速增大。在同一桩顶水平位移条件下,桩身应力由桩顶开始向下逐渐增大,达到最大应力位置后随深度增加而减小,与桩身弯矩变化一致。综合分析得出海床面以下1~5m范围为桩身弯矩和应力较大的区段,因此根据本模型的研究,在黄河三角洲地区单桩基础海上风机建设中,海床面以下1~5m范围内的钢管桩区段可能会发生疲劳破坏,成果为基础设计者提供了一定参考。
2.3 桩体变形分析
桩体承受水平荷载时,桩身的变形主要表现为水平向的挠曲变形,随着水平荷载的不断增大,桩身挠曲逐渐向深处发展。桩体在海床面处不同分析步对应水平位移如图8所示。
由2.2中表2可知不同分析步对应不同桩顶的水平位移,图8表明桩顶水平位移线性增长时,海床面处水平位移同样也呈线性增长,但是海床面处水平位移小于桩顶水平位移,每一级加载完成后,海床面处水平位移与桩顶水平位移数值对比见表3。

图7 不同桩顶位移下沿路径mises应力对比

图8 不同分析步海床面处水平位移

分析步①3456789桩顶位移②/mm01030507090112.5海床面位移③/mm05.30716.10327.06138.21446.87464.169比值④0.5310.5370.5410.5460.550.558
Note:①Step;②Displacement at the pile top;③Disp lacement at the mud sruface;④Ratio
表3表明海床面处位移约占桩顶位移的50%,但是随着桩顶荷载的不断增大,泥面处位移与桩顶位移比值呈微弱增长趋势,可能的原因是随着土抗力的逐渐发挥,海床表层土逐渐产生塑性屈服,导致位移增长速度加快。
图9为不同加载条件下沿桩身水平位移的变化,结合不同加载条件下桩身位移零点坐标(见表4)可以判断随着水平荷载的不断增大,桩身水平位移逐渐增大,桩身水平位移零点不断向下发展。当水平荷载较小时,土抗力主要由浅层土承担,随着荷载逐渐增大,表层土产生塑性屈服,深层土抗力逐渐发挥,导致桩身水平位移零点逐渐向下发展。

表4 不同加载条件下桩身位移零点坐标
Note:①Displacement at the pile top; ②Zero displacement coordinate of pile
与研究桩身应力相似,同样建立桩体挤压土体一侧由桩顶至桩底的竖直方向节点路径path1(压应变),与背向施力方向桩顶至桩底的竖直方向节点路径path2(拉应变,取绝对值),得到极限荷载作用下桩身应变图(见图10)。

图9 沿桩身水平位移曲线

图10 沿桩身应变曲线
图10表明桩体在水平极限荷载作用下无论是挤压土体一侧还是背向施力一侧,桩身应变都表现为从桩顶至桩底先增大后减小的趋势,但是应变数值均很小,最大桩身应变出均现在泥面以下3m左右,与2.2中桩身最大应力位置相同。但是对比分析path1与path2,可以判断背向施力侧的桩体应变要远大于受压侧桩体,前者应变最大值约为后者的3.26倍。
2.4 土体变形分析
当在桩头附近施加水平荷载时,浅层土体由于强度低,首先达到塑性破坏,进而桩身挠曲不断向深处发展,造成深处土体不断受到桩的挤压,随着荷载的增大,深处土体同样产生塑性屈服。图11为桩顶水平位移u=3cm时土体等效塑性应变云图,表明此时浅层土体和桩底部土体已经出现了塑性屈服,由于桩端是绑定约束,因此桩基对“施力侧”土体挤压作用有限,而模型中默认土体不抗拉,因此出现桩顶由于受压而破坏,桩端由于受拉而破坏情况。对比图11与图4可以判断随着桩顶水平位移的增大,土体塑性屈服区域由浅层土逐渐向深处发展,桩顶达到极限水平位移时,塑性区发展至海床面以下约6.2m。

图11 桩顶水平位移u=3cm时等效塑性应变云图
在桩体的挤压作用下,受挤压侧的土体会发生水平位移。由于桩体的水平挤压作用而导致海床面处的水平位移U2分布云图如图12所示。根据图12可以判断几乎整个半圆形土体区域均受到桩体挤压作用而产生水平位移U2。但是海床面处距桩心不同距离处受挤压的程度不同,U2呈半圆形放射状分布,即距离桩心相同半径的水平位移U2几乎相同,距离越远,受挤压作用影响越小,在与桩心距离约3 m范围内,土体水平位移U2随半径增大而急剧减小。

图12 海床面处水平位移U2云图
为进一步研究不同深度土体水平位移U2的分布情况,海床面以下5m范围内每隔1m建立如图12中红色箭头所示的节点路径,每一深度处沿节点路径土体位移U2的变化如图13所示。

图13 不同深度处沿路径土体位移U2分布
根据图13可以判断随着深度z的增加,距桩心相同半径处土体水平位移U2的数值逐渐减小,但是减小速度随着半径的增大而迅速下降。在同一深度处,土体水平位移U2分布与距桩心的半径R有关,半径R=3m范围内,U2数值下降速度非常快,半径3m以外U2下降速度较慢。
土体mises应力云图(见图14)也可以说明桩对土体的挤压作用。以钢管桩槽为中心的土体两侧mises应力呈现非对称分布,即深度5m范围内,被挤压侧土体的应力明显大于背向施力一侧土体,这种非均匀分布随着深度增大而逐渐消失,2.3中根据图9可以表明深度越大桩体水平位移越小,因此对土体挤压作用越小,所以导致mises应力非均匀分布逐渐消失。因此综上所述,根据本模型的研究,海床面下5m范围内土体变形受桩体水平挤压影响较大。
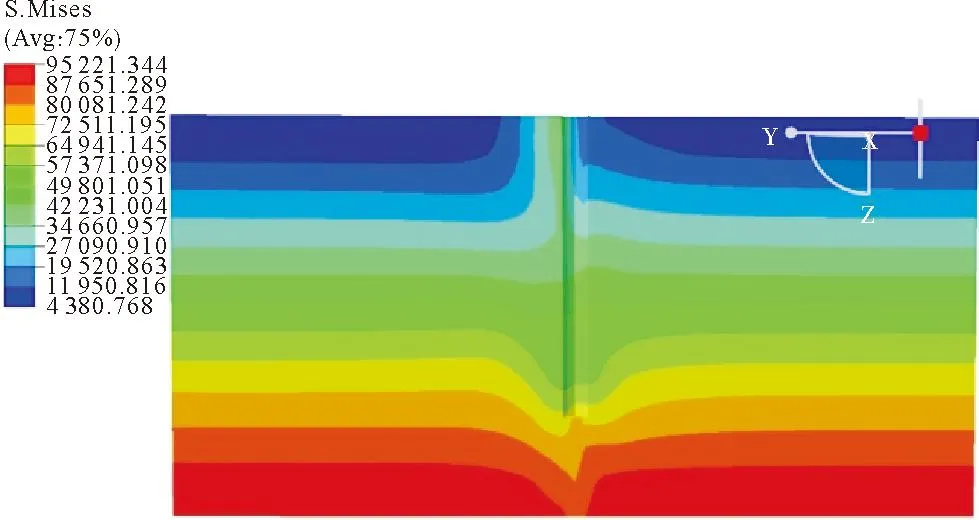
图14 土体mises应力云图
3结论
本文利用ABAQUS有限元分析软件建立桩土模型,针对海上风机单桩基础的水平极限承载力,不同桩顶位移条件下桩体内力变形以及土体变形进行了深入研究。针对本文模型,得到的结论如下:
(1) 运用位移控制法,根据桩顶荷载-位移曲线得到了模型桩单桩水平极限承载力约为375.22kN,此时对应桩顶水平位移为11.25cm。
(2) 不同桩顶位移条件下桩身最大弯矩和最大mises应力均出现在海床面以下3m左右,桩顶达到极限水平位移时桩身弯矩最大值约为2217kN·m,最大mises应力值约为56MPa。综合弯矩与应力分布可以得出海床面以下1~5m范围为桩体易发生疲劳破坏的区段。
(3) 不同加载条件下海床面处桩体位移约为桩顶位移的50%。随着水平荷载的增大,桩体水平位移逐渐增大,位移零点逐渐往深处发展。水平极限荷载作用下背向施力侧桩体应变远大于受压侧桩体应变。
(4) 随着桩顶水平位移的逐渐增大,桩体挠曲不断向深处发展,导致深层土受到挤压作用,进而使土体塑性屈服区逐渐加深。桩的挤压作用导致土体水平位移U2呈半圆形放射状分布,随着深度z的增加,距桩心相同半径处水平位移U2逐渐减小。桩的挤压作用也导致了土体内部mises应力呈现非对称分布,但是这种非对称性随着深度增加而逐渐消失。
参考文献:
[1]刘冰雪. 海上风机桩基础承载特性的三维有限元分析[D]. 大连:大连理工大学, 2009.
LIU Bing-Xue. Study on bearing capacity behavior of mono-pile foundation for offshore wind turbines using3-D FEM [D]. Dalian: Dalian University of Technology, 2009.
[2]刘红军, 李洪江. 黄河三角洲海上风机新型吸力锚基础型式分析[J]. 中国海洋大学学报(自然科学版), 2014, 44(7): 71-76.
LIU Hong-jun, LI Hong-jiang. A new suction anchor foundation of yellow river delta offshore wind power [J]. Periodical of Ocean University of China, 2014, 44(7): 71-76.
[3]Matlock H S.Correlations for design of laterally loaded piles in soft clay[C]. Houston: Proceedings of 2nd Offshore Technology Conference, 1970.
[4]Reese L C, Cox W R, Koop F D. Field testing and analysis of laterally loaded piles in stiff clay[C]. Houston: Proceedings of 7th Offshore Technology Conference, 1975.
[5]M.W. O’Neill, J. M. An Evaluation of p-y Relationships in Sands[R]. Houston:A Report to the American Petroleum Institute, 1983.
[6]American Petroleum Institute, Recommended Practice for Planning, Designing and Constructing Fixed Offshore Platforms[S]. Washington: Awerican Dexoleum Institute, 2000.
[7]Abdel-Rahman K, Achmus M. Finite element modeling of horizontally loaded monopile foundations for offshore wind energy converters in Germany[C]. Australia: International Symposium on Frontiers in Offshore Geotechnics (ISFOG), 2005.
[8]王腾, 王天霖. 粉土 p-y 曲线的试验研究[J]. 岩土力学, 2009, 30(5): 1343-1346.
WANG Teng, WANG Tian-lin. Experimental research on silt p-y curves[J]. Rock and Soil Mechanics, 2009, 30(5): 1343-1346.
[9]Achmus M, Kuo Y, Abdel-Rahman K. Behavior of monopile foundations under cyclic lateral load[J]. Computers and Geotechnics, 2009, 36(5): 725-735.
[10]梅毕祥, 杨敏. 海上风机单桩基础设计要点及有限元分析实例[J]. 海洋技术学报, 2014, 33(01): 89-94.
MEI Bi-Xiang, YANG Min. Design points and finite element analysis of monopile foundation for offshore wind turbines: case study[J]. Journal of Marine Technology, 2014, 33(01): 89-94.
[11]刘润, 李宝仁, 练继建,等. 海上风电单桩复合筒型基础桩筒共同承载机制研究[J]. 天津大学学报:自然科学与工程技术版, 2015(5). DOI: 10. 11784/tdxbz201309112.
LIU Run, LI Bao-ren, LIAN Ji-jian,et al. Bearing characteristics of pile-bucket composite foundation for offshore wind turbine [J]. Journal of Tianjin University(natural science and engeering edition), 2015(5). DOI:10.11784/tdxbz201309112.
[12]李炜, 黄旭, 赵生校,等. 海上风机基础大直径加翼单桩常重力模型试验数值仿真[J]. 水利水运工程学报, 2013(4): 6-11.
LI Wer,HUANG Xu,ZHAO Sheng-xiao,et al. Numerical simulation for 1g model test of large diameter wing-monopile for offshore wind turbine[J]. Hydro Science and Engineering, 2013, (4): 6-11.
[13]霍宏斌, 王尔贝, 陈锐,等. 一种新型重力式海上风机基础承载特性分析[J]. 地下空间与工程学报, 2013(9): 1554-1558.
HUO Hong-bin, WANG Er-bei,CHEN Rui,et-al. Bearing behavior of a novel gravity foundation for offshore wind tuebines[J]. Chinese Journal of Underground Space and Engineering, 2013(9): 1554-1558.
[14]丁红岩, 胡彩清, 张浦阳,等. 桩-筒组合基础在单层黏土中水平承载性能分析[J]. 海洋工程, 2014, 32(2): 30-37.
DING Hong-yan, HU Cai-qing, ZHANG Pu-yang, et al. Analysis of horizontal bearing capacity performance of offshore wind turbines in single-layer clay[J]. The Ocean Engineering, 2014, 32(2): 30-37.
责任编辑庞旻
Research on the Pile-Soil Interaction of Monopile Foundation Under
Horizontal Load for Offshore Wind Turbine
LIU Hong-Jun1, YIN Yan-Jing2, CHANG Ji-Qing3
(1. The Key Lab of Marine Environmental Science and Ecology, Ministry of Education, Qingdao 266100, China; 2. College of Environmental Science and Engineering, Ocean University of China, Qingdao 266100, China; 3. Qingdao Geotechnical Investigation and Surveying Research Institute, Qingdao 266032, China)
Abstract:As a kind of clean and green energy, more and more attention are paid to the offshore wind power. The offshore wind turbine will be subjected to the horizontal loads from wind、wave and flow, so the research of pile-soil interaction of monopile foundation is becoming a hot issue. By ABAQUS finite element analysis, according to this model, research shows that the ultimate horizontal displacemnent at the pile top is about 11.25cm; the bending moment and mises stress is much larger 1-5 meters below the mud surface; pile deflection and the zero displacement position stretch downward with the increase of horizontal displacement at the pile top; the soil squeezing action will cause the development of the plastic yielding range of soil, the semicircular distribution of soil horizontal displacement and the asymmetric distribution of mise stress of shallow soil.
Key words:offshore wind turbine; monopile foundation; ABAQUS;horizontal load; pile-soil interaction
DOI:10.16441/j.cnki.hdxb.20150288
中图法分类号:X144
文献标志码:A
文章编号:1672-5174(2016)03-113-08
作者简介:刘红军(1966-),男,教授,博导, 主要从事海洋工程地质方面的科研工作。E-mail:hongjun@ouc.edu.cn
收稿日期:2015-08-18;
修订日期:2015-10-26
*基金项目:国家自然科学基金项目“波浪作用下海上风电场桩基土体液化响应研究-以黄河三角洲为例”(41572247);山东省科技攻关项目“黄河三角洲海上风电场桩基设计关键技术研究”(2014GGX104007)资助
引用格式:刘红军, 尹燕京, 常季青. 水平荷载下海上风机单桩基础桩土相互作用研究[J]. 中国海洋大学学报(自然科学版), 2016, 46(3): 113-120.
Supported by Research on Liquefaction Reponse of Soil Body Around Pile Foundation of Offshore Wind Turbine under Wave Conditions-Taking Yellow River Delta as the case(41572247); Research on Key Techniques in Pile Foundation Design of Offshre Wind Farm in Yellow River Delta(2014GGX104007)

