不同设计使用年限下实用设计表达式系数的求解

蒋济同, 吴颖欣, 杜德润

(中国海洋大学土木工程系， 山东 青岛 266100)



不同设计使用年限下实用设计表达式系数的求解

蒋济同, 吴颖欣, 杜德润

(中国海洋大学土木工程系， 山东 青岛 266100)

摘要：基于可靠度分析理论以及荷载标准值等数据的调整，分别运用JCSS法与Monte Carlo法计算出运用于结构领域的新的目标可靠指标并依据不同可变荷载的概率统计模型计算出对应于不同设计使用年限的调整系数及数理统计参数。以最小二乘法为准则，借助Matlab里的数学算子，分别采用穷举优化搜索法和极值理论求解法计算出实用设计表达式中荷载分项系数及结构重要性系数，并计算出标准值等数据调整前后的单构件的相对误差增量。从工程实际应用出发，在荷载、抗力分项系数均按现行规范采用的情况下，计算出能同时体现不同安全等级与设计使用年限的结构重要性系数，并分析了现行规范中采用的结构重要性系数取值对应的包络范围，对今后结构设计提供参考借鉴。

关键词：可靠度； 安全等级； 设计使用年限； 分项系数； 结构重要性系数

JIANG Ji-Tong， WU Ying-Xin， DU De-Run. Solution on the coefficients of design formulation for the pragmatic usage under different design working lives[J].Periodical of Ocean University of China, 2016, 46(3): 121-125.

《建筑结构设计统一标准》[1]经调查、实测并经数理统计处理后，得到了全国范围内永久荷载、可变荷载的概率分布函数和统计参数，是中国目前可靠度分析的基础。现行的《工程结构可靠性设计统一标准》[2]采用“校准法”确定了今后设计时采用的可靠指标。在校准可靠指标β时，考虑了具有代表性的14种构件、不同的荷载效应比ρ以及三种简单荷载组合，根据编制标准时各随机变量的标准值计算其统计参数。新版《建筑结构荷载规范》[3]对中国的结构构件安全度做了调整，整体设置水平有所提高，因此可靠指标β也应随之改变,提高后的可靠指标与荷兰、丹麦等国家的标准相接近。

从简单到复杂或精确程序的不同，国内外先后采用了一次二阶矩法、二次二阶矩法、蒙特卡洛(Monte-Carlo)等方法进行可靠指标求解。目前行业内广泛采用一次二阶矩法中的验算点法和蒙特卡洛法中的重要抽样法进行可靠指标求解。验算点法将非线性功能函数作一次泰勒级数展开，并使用当量正态化后的随机变量平均值和方差进行求解，蒙特卡洛法运用计算结构的失效概率来求解可靠度，对于结构可靠度不高即失效概率较大的情况，有较高的效率。

对于一般的结构构件，若根据规定的β值直接进行截面设计或截面复核，计算工作量大且不实用，设计人员习惯于采用基本变量的标准值和分项系数进行结构设计，使设计表达式所设计出的结构所具有的可靠指标尽可能地接近预定的目标可靠指标。目前均采用以最小二乘法为准则，进行实用表达式中的分项系数求解，使用分项系数设计结构时无需进行概率方面的运算，并已积累了大量的工程实践经验。

《工程结构可靠性设计原理》[4]和《土木工程结构可靠度理论与设计》[5]等文献中给出了确定分项系数的原则和方法。但众多文献推荐的步骤中，是在假定结构重要性系数γ0已知的前提下运用穷举法进行求解。这一前提只体现安全等级，无法与《民用建筑通则》[6]中3.2.1条规定以及《建筑结构可靠性设计统一标准》[7]第7.0.3条规定对应，《结构的设计使用年限与结构重要性系数》[8]、《通用设计表达式中荷载与抗力分项系数的研究》[9]等文献中也提到了关于此方面的问题与看法。

以荷载和抗力的数理模型为基础，系统求解不同设计使用年限所对应的数理统计参数与实用设计表达式中相应系数，弥补了目前可靠度研究文献中的不足。针对目前众多文献中采用的穷举求解法的不足，运用Matlab中fminsearch函数，在不改变抗力分项系数γR和不提前设定γ0具体值的前提下，求解出与设计使用年限相匹配的荷载分项系数γG、γQ以及结构重要性系数γ0，与穷举法求解对比，省去穷举法的叠加爆炸计算时间，使实用设计表达式中相应系数能同时体现建筑物安全等级与设计使用年限，并根据计算结果分析了结构重要性系数γ0取值对应的包络范围。

1新的目标可靠指标β

新版《建筑结构荷载规范》对中国的结构构件安全度做了调整，楼面可变荷载标准值由1.5kN/m2提高到了2.0kN/m2，风荷载也由原来的30a一遇修订为50a一遇。因此除了永久荷载、构件抗力的标准值和与之对应的参数无需调整外，可变荷载的统计参数需按其数理统计模型(极值I型)作相应的调整(见表1)。因可变荷载标准值的增大，荷载效应比值ρ也相应地增大了0.33(楼面)和0.1(风)。

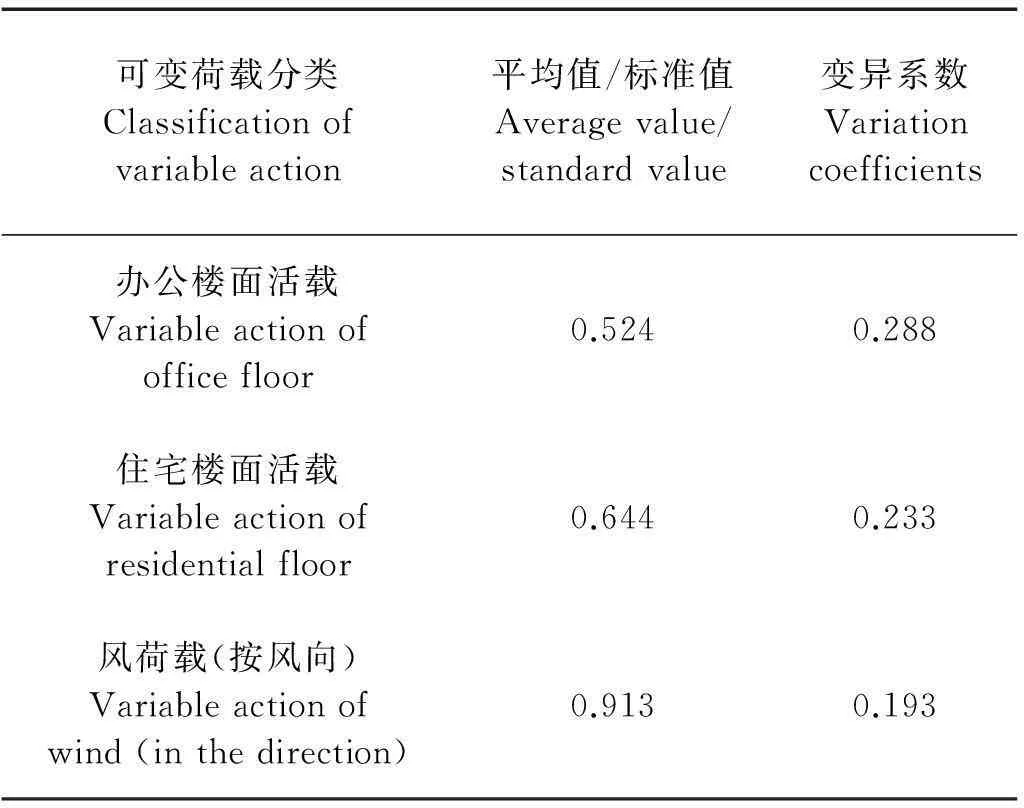
表1　各随机变量设计基准期统计参数

目前求结构目标可靠指标β的方法主要有验算点法(JCSS法)、Monte Carlo法[10]、Matlab优化工具箱[11]等，用新调整的统计参数，分别用验算点法和Monte Carlo中重要抽样法，运用Matlab编程对具有代表性的14种构件，对应不同的荷载效应比ρ以及3种不同的简单荷载组合进行目标可靠指标β的计算。根据计算结果对比分析，Monte Carlo自身3次结果对比相对误差达到小数点后4位，且JCSS法和Monte Carlo法计算结果相对误差小于0.001，即认为Monte Carlo法已达到稳定且JCSS法具有很高的精度。两种方法计算出这14种构件属延性破坏者平均值为3.65。根据对现行结构设计规范安全度校核分析结果，参考了《浅议建筑结构设计可靠度的有关问题》[12]等文献资料，同时综合考虑安全与经济等因素，以及规范的继承性，建议对一般工业与民用建筑的各种构件(安全等级为二级)，属延性破坏的目标可靠指标取为3.6，属脆性破坏的目标可靠指标取为4.1(见表2)。

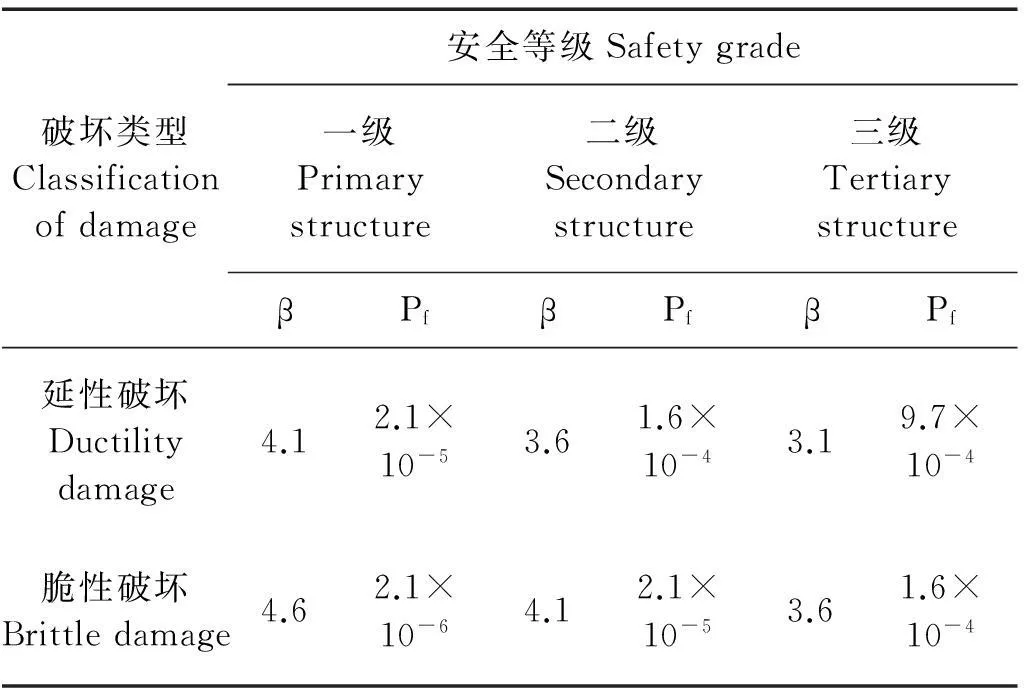
表2　结构构件承载能力极限状态设计时采用的

2运用Matlab中fminsearch函数求解实用设计表达式相应系数

针对众多文献资料中推荐确定分项系数的步骤，以《工程结构可靠性设计原理》、《土木工程结构可靠度理论》为代表，均是在已假定结构重要性系数γ0为已知确定数的前提下，由14种具有代表性构件、分别在3种简单荷载组合和常用的荷载作用效应比ρ作用下，利用最小二乘法以相对总误差I最小为准则优化确定，即确定的荷载分项系数γG、γQ和抗力分项系数γR使下式最小：

(1)

式中βij为按分项系数方法计算的可靠指标。

《建筑结构设计统一标准》中5.0.2条规定，对于安全等级为一、二、三级结构构件，结构重要性系数γ0分别对应取1.1、1.0和0.9。这一假设前提无法与《民用建筑通则》中第3.2.1条按设计使用年限将建筑物重要性分四类以及《建筑结构可靠性设计统一标准》中7.0.3条关于设计使用年限的规定对应，即假设同是安全等级为二级，因设计使用年限的不同，结构重要性系数γ0也应有相应的调整，不应恒定为1.0。结构重要性系数应由结构构件的安全等级与结构设计使用年限共同确定，在求解之前应是未知量。

在未知结构重要性系数γ0的情况下，基于可靠度分析理论，可编写程序利用穷举法不断优化搜索取值空间求解，也可运用Matlab中fminsearch函数代替穷举法求解相应系数，即可求取因变量相对总误差I取最小值时对应的自变量γG、γQ和γ0。前者耗费时间较多，但可根据实际需要人为规定变化级差；后者求解速度快，耗费时间少且最精确，但不可人为规定变量变化级差。

在相同前提条件下，将新版《建筑结构荷载规范》标准值及重现期调整前后的二级结构构件在设计基准期为50a的数理统计参数带入程序计算(见图1、2)。

图1　调整前T=50，I与γG、γQ的关系

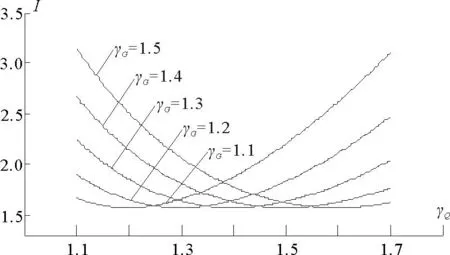
图2　调整后T=50，I与γG、γQ的关系

由图可见，对于设计使用年限为50a、安全等级为二级的结构构件，标准值及重现期调整之前，γG为1.2、γQ为1.4、γ0为1.000;经过新版《建筑结构荷载规范》标准值及重现期调整后，即取新的目标可靠指标，在抗力分项系数γR不变前提下，γG为1.3、γQ为1.4、γ0为0.959。

由两图中I值可计算出单个构件在每种简单荷载组合及荷载效应比值ρ作用情况下的相对误差值，调整前后单构件在不同荷载组合下相对误差分别约为5.63%、9.45%，对比调整前后单构件的相对误差的差值(见图3)，可以看出不同构件(依次为钢轴压、偏压、薄钢轴压、偏压、钢筋混凝土轴拉、轴压、大偏压、受弯、受剪、砖石轴压、偏压、受剪、木结构轴压、受弯)在不同的简单荷载组合下相对误差的增量不同，且调整后的相对误差总体呈现增长趋势，应考虑采用加权求解实用设计表达式中分项系数和结构重要性系数，以使相对误差控制在允许误差界限内。

3不同设计使用年限实用设计表达式中结构重要性系数优化求解

《工程结构可靠性设计统一标准》增加了楼面和屋

图3　调整前后，单构件在不同简单荷载组合

面可变荷载考虑设计使用年限的调整系数γL，使得可靠度与后续使用年限建立联系。确定楼面可变荷载考虑设计使用年限的调整系数γL时，可通过可变荷载标准值校准或通过概率分布函数的校准两种方法确定，本文按照通过概率分布函数的校准确定调整系数γL，则有

(2)

式中:kQ为可变荷载Q设计基准期最大值的平均值与标准值的比值;δQ为可变荷载Q的变异系数。

根据大量的统计分析，一般假定以上3种可变荷载均服从极值I型分布，且设计基准期T内最大荷载分布函数为：

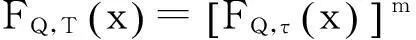
(3)

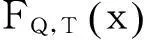
楼面活荷载可分为楼面持久性荷载和楼面临时性荷载两类，在办公楼楼面活荷载、住宅楼面活荷载保证率分别为99.0%和97.4%设置水平(与现行规范相同)下，计算出不同设计使用年限下的楼面荷载取值标准。荷载标准值与设计基准期T内的保证率可简化为：

(4)

故楼面活荷载的均值和方差可按下列式求解：

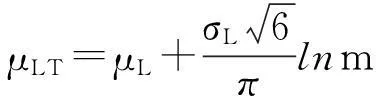
(5)

σLT=σL，

(6)

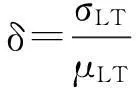
(7)

式中：μLT、σLT分别为设计基准期T内的均值和标准差；μL、σL分别为任意时点的均值和标准差；m为设计基准期T内荷载平均变动次数。

风荷载统计参数求解的基本思想可参照《既有建筑结构构件的安全性分析》[13]、《60年设计基准期下可变荷载标准研究》[14]等文献中建议取建筑物的目标使用期作为确定基本风压的重现期，根据极值I型分布数学模型以及设计基准期内发生超越荷载设计值的概率一致的原则进行求解，即

FQ,T1(QT1,k)=FQ,T2(QT2,k)。

(8)

式中QT1,k和QT2,k分别为T1、T2设计基准期下风荷载最大值概率分布函数。

不同设计使用年限的调整系数γL以及数理统计参数(平均值/标准值K，变异系数δ)的计算结果(见表3)。

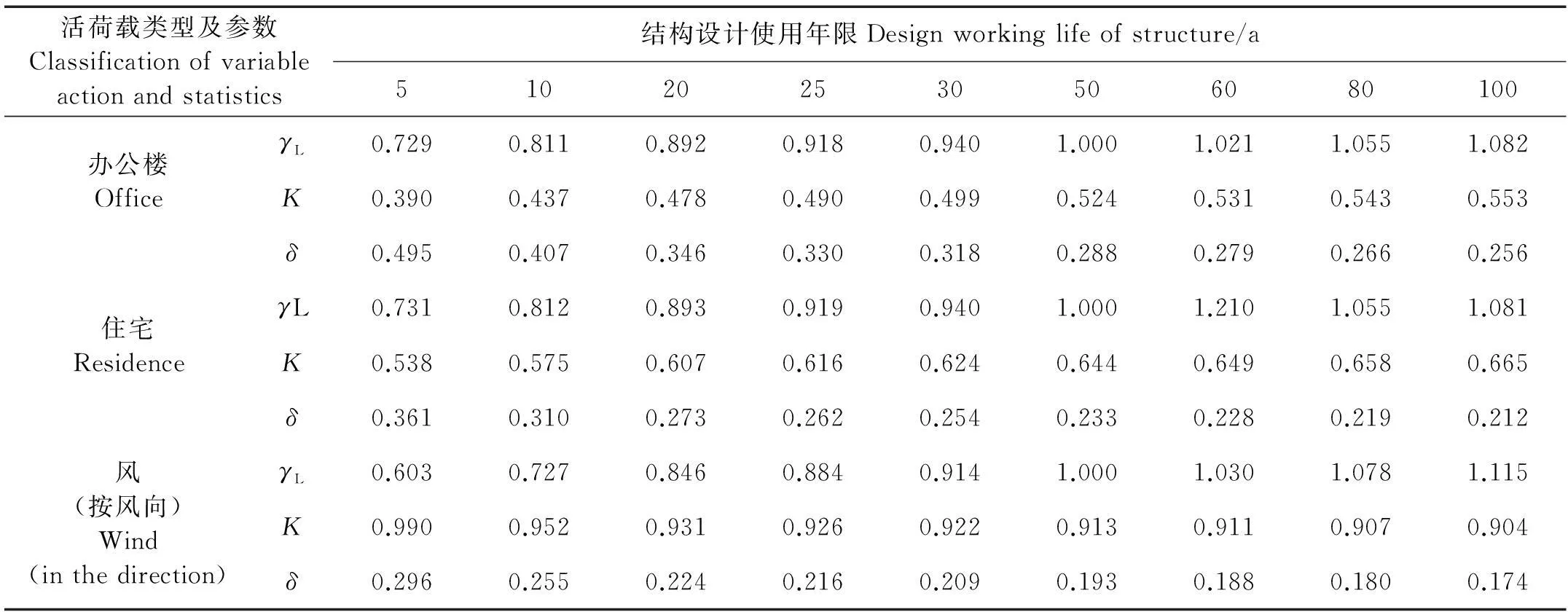
表3　不同设计使用年限的调整系数及统计参数

因现行规范仍然采用荷载分项系数γG为1.2、γQ为1.4，及相应14种构件抗力分项系数γR，所以在实用设计表达式中的分项系数均不变情况下，采用提高后的可靠指标(3.6、4.1)对不同安全等级以及设计使用年限的结构重要性系数γ0进行求解，计算结果(见表4)。

表4　不同安全等级及设计使用年限γ0

由表4可知，在荷载分项系数γG、γQ及相应的14种构件的抗力分项系数γR均采用现行规范值的情况下，对于安全等级为一、二、三级结构构件，对于不同设计使用年限，结构重要性系数γ0并非为定值(1.1、1.0、0.9)，即《建筑结构设计统一标准》中5.0.2条规定并不能包络所有情况，结构重要性系数γ0是与结构安全等级以及结构设计使用年限成正相关关系。同一安全等级，设计使用年限为100a的结构构件与设计使用年限为50a的结构构件相比、设计使用年限为50a的结构构件与设计使用年限为20a的结构构件相比，均相当于结构安全等级提高一级。

现以对结构安全等级为二级的结构构件分析为例，若按《建筑结构设计统一标准》中要求对不同设计使用年限均取1.0，对于设计使用年限20a以下结构构件的设计不经济，对于20～50a结构构件偏保守，对于50～60a结构构件较适用，对于60a以上结构构件不安全。其他不同安全等级对应不同设计使用年限的结构重要性系数γ0也可从

表4中得到现行规范中采用的系数的适用范围。

目前实际鉴定工程中经常出现结构抗震能力满足和承载能力不满足的情况，因为《建筑抗震鉴定标准》[15]中将建筑分为A、B、C类(分为按后续使用30a、40a、50a进行抗震鉴定)，而承载力方面均按50a的荷载考虑。

表4中的内容很好地使鉴定工作中的抗震和承载力相对应，例如一栋A类建筑，在抗震考虑后续使用年限30a的基础上，承载力方面也可按30a的荷载系数加载，使鉴定工作更加合理。

4结论

(1)根据现行规范数据的调整，运用JCSS法与Monte Carlo法求解的结构目标可靠指标β均应在现行规范(3.2、3.7)的基础上提高0.4，相当于失效概率降低一个数量级；

(2)将计算出的不同设计使用年限的调整系数以及数理统计参数运用带入Matlab程序中计算，比较得出fminsearch函数编程较穷举优化搜索法速度更快且精确；

(3)目前规范在可靠指标β采用(3.2、3.7)前提下，规定实用设计表达式中γG、γQ和γ0分别为1.2、1.4和1.0。按照新的目标可靠指标β(即3.6、4.1)求解出实用设计表达式中γG、γQ和γ0分别为1.3、1.4和0.959。根据相对总误差I值可计算出调整前后的单构件的相对误差分别为5.63%、9.45%，且目标可靠指标调整后的相对误差总体呈增长趋势；

(4)在γG、γQ和γR均采用现行规范值的情况下，求解出结构重要性系数γ0，计算结果表明不同安全等级及设计使用年限γ0应采用不同的数值,并对应总结出规范中结构重要性系数较适用于50～60a结构构件设计。

参考文献：

[1]中国建筑科学研究院. 建筑结构设计统一标准[S]. 北京：中国建筑工业出版社， 1984. GBJ68-84.

National Standard of China. GBJ68-84， Unified standards for the design of structures[S].Beijing:China Architecture & Building Press,1984.

[2]国家标准委员会. GB50153-2008工程结构可靠性设计统一标准[S]. 北京： 中国建筑工业出版社， 1984.

National Standard of China, GB 50153-2008， Unified standard for reliability design of engineering structures[S]. Beijing: China Architecture & Building Press, 2008.

[3]国家标准委员会.GB50009-2012 建筑结构荷载规范[S]. 北京： 中国建筑工业出版社， 1984.

National Standard of China. GB50009-2012, Load code for the design of building structures[S]. Beijing: China Architecture & Building Press, 2012.

[4]贡金鑫, 魏巍巍. 工程结构可靠性设计原理[M]. 北京： 机械工业出版社, 2007.

Gong Jinxin, Wei Weiwei. Principle of engineering structure reliability design[M]. Beijing： Machinery Industry Press, 2007.

[5]杨伟军, 赵传智. 土木工程结构可靠度理论与设计[M]. 北京： 人民交通出版社, 1999.

Yang Weijun, Zhao Chuanzhi. Reliability Theory and design of civil engineering structures[M]. Beijing: China Communication Press, 1999.

[6]国家标准委员会. GB50352—2005民用建筑设计通则[S]. 北京： 建筑工业出版社， 2005.

National Standard of China. GB 50352-2005， Code for design of civil buildings [S]. Beijing: China Architecture & Building Press， 2005.

[7]国家标准委员会. GB50068-2001建筑结构可靠性设计统一标准[S]. 北京： 建筑工业出版社， 2001.

National Standard of China. GB50068-2001 (2001)， Unified standard for reliability design of building structures[S]. Beijing: China Architecture & Building Press, 2001.

[8]史志华. 结构的设计使用年限与结构重要性系数[J]. 建筑科学, 2000, 16(6): 32-33.

Shi Z H. On Structural Design Working Life and the Importance Factor of Structure[J]. Building Science, 2000, 16(6): 32-33.

[9]龚云平. 通用设计表达式中荷载与抗力分项系数的研究[D]. 西安: 西安建筑科技大学, 2006.

Gong Yunping. Analysis on Load and Resistance Factors in General Design Expression[D]. Xi′an: Xian University of Architecture and Technology, 2006.

[10]董艳秋, 田敬博. 蒙特卡洛法结构可靠性分析[J]. 黑龙江工程学院学报, 2010 (1): 27-29.

DONG Yan qiu, TIAN Jing bo. Structural reliability analysis of Monte Carlo method[J]. Journal of Heilongjiang Institute of Technology, 2010 (1): 27-29.

[11]张高峰, 贾建勋, 张大巍. 应用 Matlab 优化工具箱求解可靠度问题[J]. 工程地质计算机应用, 2004 (1): 5-7.

Zhang Gaofeng, Jia Jianxun, Zhang Dawei. Solve reliability problem with matlab optimization toolbox[J]. Engineering Geology Computer Application, 2004(1): 5-7.

[12]张周. 浅议建筑结构设计可靠度的有关问题 [J]. 建筑结构, 2011 (2)： 11-15.

Zhang Z. Argument on relevant problem of credibility of buidling structure design[J]. Building Structure, 2011 (2)： 11-15.

[13]顾祥林, 许勇, 张伟平. 既有建筑结构构件的安全性分析[J]. 建筑结构学报, 2005, 25(6): 117-122.

Xianglin GU, Yong XU, Zhang W. Safety analysis of structural members of existing buildings[J]. Journal of Building Structures, 2005, 25(6): 117-122.

[14]王凯, 吕令毅, 周建章, 等. 60 年设计基准期下可变荷载标准研究[J]. 工程建设与设计, 2009 (10): 19-22.

Wang K, LV Ling yi, ZHOU Jian zhang, et al. Studyon the variable load in 60-year design reference period[J]. Construction & Design for Project, 2009(10):19-22.

[15]国家标准委员会. GB50023-2009 建筑抗震鉴定标准[S]. 北京：建筑工业出版社，2005.

National Standard of China. GB50023-2009， Standard for seismic appraiser of building[S]. Beijing: China Architecture & Building Press， 2009.

责任编辑陈呈超

Solution on the Coefficients of Design Formulation for the Pragmatic Usage Under Different Design Working Lives

JIANG Ji-Tong, WU Ying-Xin, DU De-Run

(Department of Civil Engineering, Ocean University of China, Qingdao 266100, China)

Abstract:Based on the reliability analysis theory and the adjusted characteristic values of an action, the new target reliability index, which is applied in structure area, is calculated using the JCSS method and Monte Carlo method. Moreover, the adjustment factors and mathematical statistics parameters corresponding to different design working lives are computed according to different probability distribution models of variable actions. Especially, in theoretical analysis, based on the least square method, the partial factors of safety for load and the coefficients for importance of structures were developed by using the method of enumeration in association with optimization search and the method of extremum theory respectively with the function of Matlab. The relative error increments of the single component are then solved before and after the adjustment of the data (e. g. characteristic values). As for practical applications, the different coefficients for importance of structures corresponding to different levels of safety and design working lives under various situations are obtained when the partial safety factor for load and the partial safety factor for resistance meet the requirements of the current standard. Finally, the application envelops of different coefficients for importance of structures are analyzed for the future structure design.

Key words:degree of reliability; safety class; design working life; partial safety factor; coefficient for importance of a structure

DOI：10.16441/j.cnki.hdxb.20140192

中图法分类号：TU318

文献标志码：A

文章编号：1672-5174(2016)03-121-05

作者简介：蒋济同(1966-)，男，教授。E-mail:baomiaoxinzi@163.com

收稿日期：2014-06-10；

修订日期：2015-01-12

引用格式：蒋济同, 吴颖欣, 杜德润. 不同设计使用年限下实用设计表达式系数的求解[J]. 中国海洋大学学报(自然科学版), 2016, 46(3): 121-125.