基于RBF神经网络的机器人平滑圆弧轨迹规划*
辛大欣 刘少贞
(西安工业大学电子信息工程学院 西安 710021)
基于RBF神经网络的机器人平滑圆弧轨迹规划*
辛大欣刘少贞
(西安工业大学电子信息工程学院西安710021)
摘要针对一般圆弧插补算法收敛性和稳定性差,逼近效果不理想的问题,提出基于RBF神经网络的圆弧轨迹规划方式。论文从运动学角度出发,分析求解工业四轴机器人运动学正逆问题,建立其D-H数学模型和空间三维模型。通过圆弧轨迹经过的空间三点,求出空间圆弧的参数方程;在Matlab软件中,仿真RBF神经网络规划的圆弧轨迹曲线,结果表明RBF神经网络所规划轨迹平滑稳定,收敛速度快,逼近误差小,从而证明RBF神经网络对机器人轨迹规划的可行性与必要性。
关键词机器人; 轨迹规划; 圆弧; RBF神经网络
Trajectory Planning of Robotic Smooth Arc Based on RBF Neural Network
XIN DaxinLIU Shaozhen
(School of Electronics Information Engineering, Xi’an Technological University, Xi’an710021)
AbstractTo solve problem that the convergence and stability of the arc interpolation algorithm is not ideal, this paper proposes a circular trajectory planning method based on RBF neural network. From the point of view of kinematics, the normal inverse kinematics problem of four axis robot is analyzed, and the mathematical model of D-H and 3D model is established. Through the space 3 points of circular arc track, the parameter equation of space circular arc is obtained. In the Matlab software, emulating the trajectory of the circular interpolation algorithm based in RBF neural network planning, the results show that the trajectory planning of RBF neural network is smooth and stable, the convergence speed is fast and the approximation error is small. So the feasibility and necessity of RBF neural network for robot trajectory planning are proved.
Key Wordsrobot, trajectory planning, arc, RBF neural network
Class NumberTP18
1引言
机器人是一种机电一体化数字设备,是当今工业自动化的重要构成部分。轨迹规划是在机器人运动学和动力学基础上对机器人进行的底层规划,是机器人轨迹跟踪控制的基础,也是机器人执行作业任务的基础[1]。平稳、快速的轨迹规划算法对提高机器人系统的整个性能非常重要。
在两个取料机器臂相互协调运作的过程中,机器人末端过空间三点作圆弧运动。为了使机器人在一定的时间内快速、平稳地从初始目标到达规定的目标状态,需要根据机器人末端执行器的位姿求解出机器人各个关节位置,从而产生机器臂的控制系统所需的输入,使机器臂能够执行运动。常用插值方法来拟合运动轨迹,但是为了保证优化精度,必会增加中间路径点个数,这样函数的收敛性和稳定性会变差,逼近效果不理想[2]。而径向基函数RBF神经网络具有良好的函数逼近能力,通过对非线性插值节点的学习,可以逼近任意给定的非线性函数。
2运动学分析
机器人运动学是机器人学最基础的内容,主要研究机器人工作空间内其末端执行器的位姿和各关节变量之间的相互关系,包括正运动学和逆运动学问题[3]。本次研究的四轴机器人是四自由度关节型机器人,可以通过分析工业四轴机器人的系统结构,在其每个关节上建立一个坐标系,利用坐标系之间的关系来描述末端执行器的位姿[4]。
D-H法是一种建立相对位姿的矩阵方法,用齐次变换描述每一个连杆相对固定参考系的空间几何关系,然后用一个4*4阶其次变换矩阵描述相邻两个连杆的空间关系,从而推导出末端执行器坐标系相对于基座标系(规定参考系)的等价其次变换矩阵,建立机器臂的运动方程。
机器人简易结构图如图1所示,根据D-H建模法,建立四轴机器人的连杆坐标系如图2所示,D-H连杆参数如表1所示。
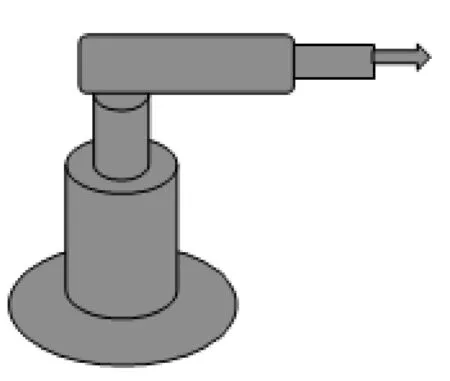
图1 机器人简易结构图

图2 工业四轴机器人的连杆坐标系
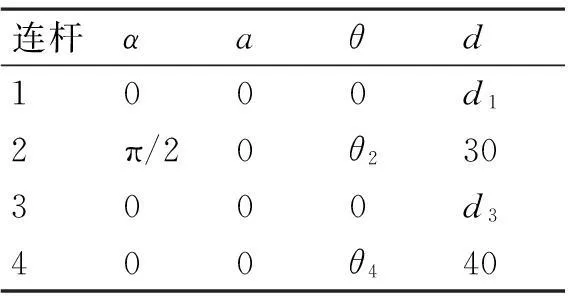
连杆αaθd1000d12π/20θ2303000d3400θ440
末端执行器的位姿可以用4*4阶矩阵表示:
(1)
其中nx,ny,nz为机器人法向矢量;ox,oy,oz为方向矢量;px,py,pz为位置坐标。
1) 机器人运动学正解问题:已知机器人连杆长度和各个关节角度,求解末端执行器相对基坐标。对于如图2所示机器人运动关系,可由连杆i对i-1相对位置的四个齐次变换矩阵表示,将D-H连杆参数代入机器人各关节的变换矩阵,确定Ai(i=1,2,3,4)变换矩阵的值,连乘四个变换矩阵,得到机器人正向运动学的解。
Ai=Rot(zi-1,θi)Trants(0,0,di)trants(ai,0,0)Rot(xi,αi)
(2)
运用D-H表示法建立机器人运动学方程:
T=A1A2A3A4

(3)
从而可得机器人的空间位姿值:
ax=sinθ2
ay=-cosθ2
az=0
px=(1+d3)sinθ2
py=-(1+d3)cosθ2
pz=d1
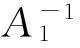
A-1T=A2A3A4
(4)
将A1的逆矩阵和A2,A3,A4代入式(4),得:
(5)
式(5)中等号左右两边矩阵对应元素相等,在已知n,o,a,p情况下,便可以求出关节变量d1,θ2,d3,θ4,求得结果如下:
d1=pz
3建立机器人运动学模型
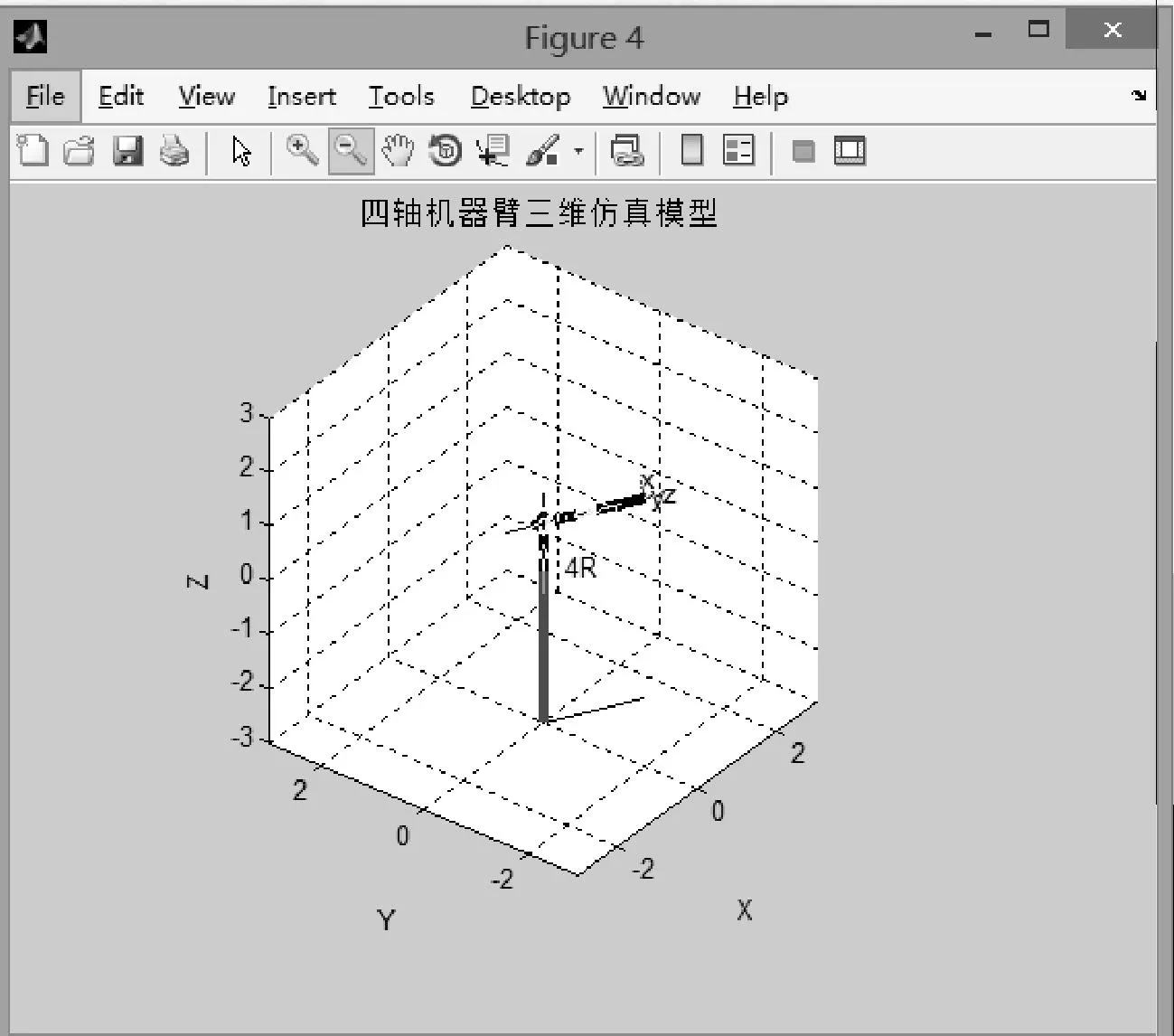
图3 工业四轴机器人运动模型
利用Matlab/robotics toolbox建立机器人模型,可以有效地对机器人运动学,轨迹规划进行仿真[5]。通过仿真可以直观地分析机器人各个关节的运动情况,得到所需数据。以验证设计的参数是否合理,达到预定的目标。用robotics toolbox工具编写程序,建立机器人三维模型如下:
Ll= link([0 0 0 1 1],'standard');
L2= link([pi/2 0 0 0 0],'standard');
L3= link([0 0 0 1 1],'standard');
L4= link([0 0 0 1 0],'standard');
r=robot({Ll L2 L3 L4 },'4R');
r.name='4R';
drivebot(r);
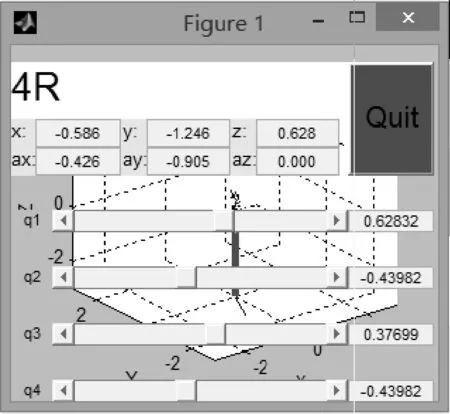
图4 机器人滑块控制图
通过移动图4中代表关节变量的四个滑块来驱动机器人运动,它的参数确定了执行器末端的位姿。为验证所建立的机器人三维模型的正确性,在机器人位姿的约束条件下,随机选取几组关节变量的值,分别代入机器人滑块控制图与运动学方程得出机器人末端设定值与实际位置信息。
四组关节变量值为
q1=[0.1280.553-1.230-0.278]
q2=[-0.1530.7251.627-0.346]
q3=[0.245-0.4681.0140.348]
q4=[0.3450.9230.992-0.572]
末端设定位置与实际位置信息比较如表2所示,Matlab具有强大的计算与仿真功能,通过其计算的运动学方程结果是比较准确的[6],分析表中数据,其实际值与设定值误差小,说明所建立的模型比较可靠。
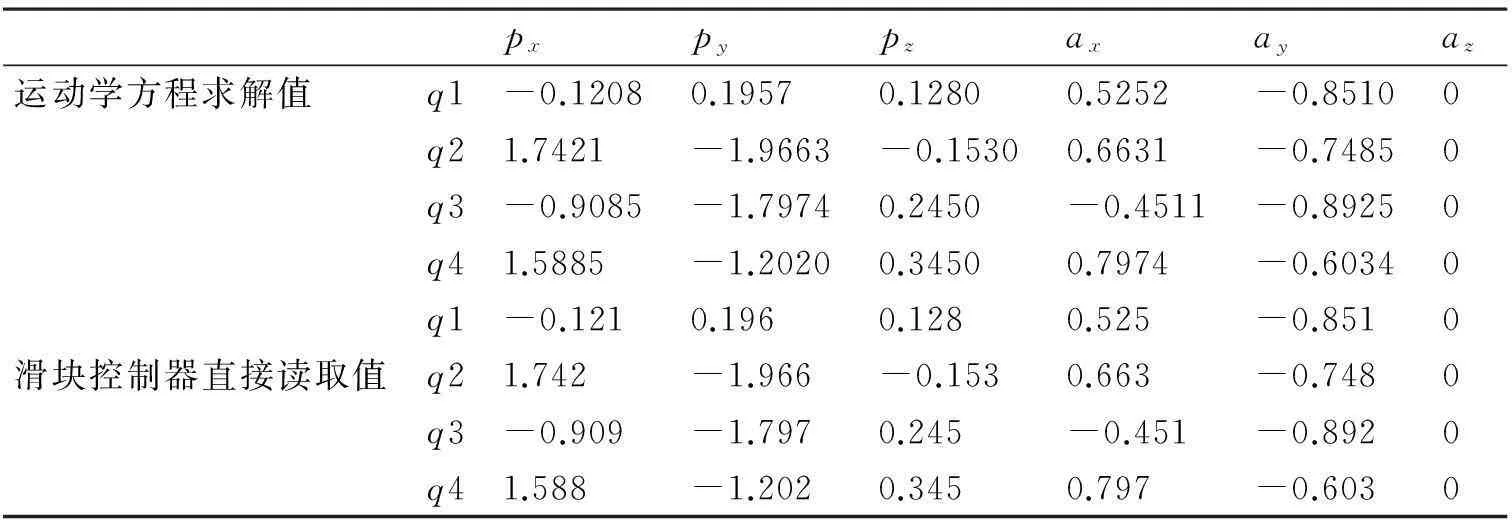
表2 运动学方程求解值与滑块设定值比较
4圆弧运动轨迹规划实现过程
1) 圆弧插补算法
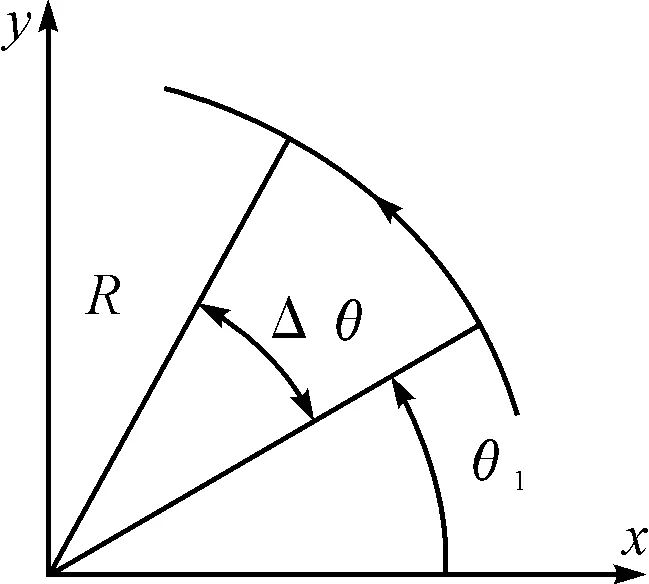
图5 圆弧插补
轨迹规划既可以在关节空间中进行,也可以在笛卡尔空间进行[7]。对于关节变量空间的规划来说,要规划关节变量的时间函数,以便描述机器人的预定任务。在笛卡尔空间规划中,要规划机器人手部末端位置的时间函数,而相应的关节位置可根据机器人的反向运动学导出[8]。关节空间轨迹规划的方法简单,不会产生奇异位置,但对于轨迹有严格要求的,需要在笛卡尔空间规划。
已知p1,p2,p3分别为圆弧轨迹的起始路径点、中间路径点以及终止路径点。这三点组成一个平面圆弧,也就是圆弧平面与基座标系的平面xoy重合[9]。已知不在一条直线上的此三点及这三点对应的末端执行器的姿态。
由p1、p2、p3确定圆弧半径R,总圆心角φ=φ1+φ2,即
(6)
在TS时间内关节角位移量为Δθ=TSV/R,由如图5的几何关系,求出插补点坐标。
总的插补步数:
N=φ/Δθ+1
(7)
对pi+1点坐标,有:
(8)
从而可求得各坐标轴的位移量:
(9)
此插补算法利用了圆的参数方程,整个计算过程中,具有以下特点:
(1)由式(6)、式(8)知各插补点一定在圆弧上;
(2)以圆心角为参数,步进角θ为增量,解决了插补圆弧跨象限时插补点的符号判断问题,可适应于不同象限圆弧的插补;
(3)sinθi和cosθi只作为中间过度量,不需要计算,从而避免了复杂的三角函数运算,提高了运算速度。
(4)θ为定值,其值的正负表示插补的方向。通常规定逆时针插补时为正,顺时针插补时为负。
工业机器人的轨迹规划仿真可以详尽、直观描述机器人的运动过程。为了验证算法的有效性,从已知的圆弧参数方程与给定的三点,设定步长,获得圆弧插补点坐标,在Matlab中拟合仿真,得到圆弧轨迹曲线[10],但是在为了追求拟合的轨迹曲线快速,平滑,且是理想的半圆弧,必须增加插补点,但是随着插补点的增多,计算量增大,曲线的逼近效果会不理想,拟合的曲线不平滑,因此需要对插补点的拟合方法进行优化[11],使其快速,逼近效果理想,这就需要用到RBF神经网络来拟合插补点了。
2) 基于RBF神经网络的轨迹规划
RBF神经网络的学习等价于在多维空间中寻找训练数据的最佳拟合平面,隐层的每一个神经元的传递函数都构成拟合平面的一个基函数。与BP神经网络相比,RBF网络的规模大,且学习速度,函数逼近、模式识别和分类能力更优[12]。
RBF神经网络是一种三层前向网络,输入层到隐含层的基函数输出是非线性映射,隐含层到输出则是线性的。RBF网络权值算法是单层进行。工作原理采用聚类功能。训练得到输入数据聚类中心。通过σ值,调节基函数的宽度。对输入一组数据,神经网络只有一个神经元被激活,忽略其它神经元的激活程度[13]。径向基神经网络(RBF)的设计,有很多函数。
本次选用newrb()函数采用迭代方法有效设计RBF神经网络,函数迭代一次,神经元加一个,直到平方和误差下降到目标误差以下,或者神经元个数达到最大。
Net=newrb(P,T,GOAL,SPREAD,MN,DF),其中GOAL是目标误差,MN是最大神经元个数,DF是迭代过程显示频率。
在Matlab仿真软件中,将圆弧插补算法获得的插值点坐标作为数据样本,给定训练误差,通过大量实验调节RBF中的扩展参数以及神经元个数,用RBF神经网络得到网络训练的误差性能曲线,并运用仿真函数进行曲线拟合,得到需要的圆弧轨迹及机器人四个关节变量函数曲线[14]。
5实验结果及分析
为了验证该算法的有效性,在Matlab环境下实验仿真。试验中设定过圆弧轨迹的三点坐标分别为p1(25,0,10),p2(50,25,10),p3(75,0,10),通过圆弧参数方程,获取插补点坐标,用在Matlab中建立的RBF神经网络对其拟合,圆弧轨迹曲线如图6所示,图中的星号是给定的三点坐标,坐标变化曲线图7所示[15]。在拟合四个关节变量曲线时,设定时间为15s,步长为0.01s,,获取150组值做样本,设定RBF神经网络误差精度0.001,通过调节各参数,进行样本训练,误差训练性能曲线如图8所示,仿真得出的四个关节变量曲线如图9所示。
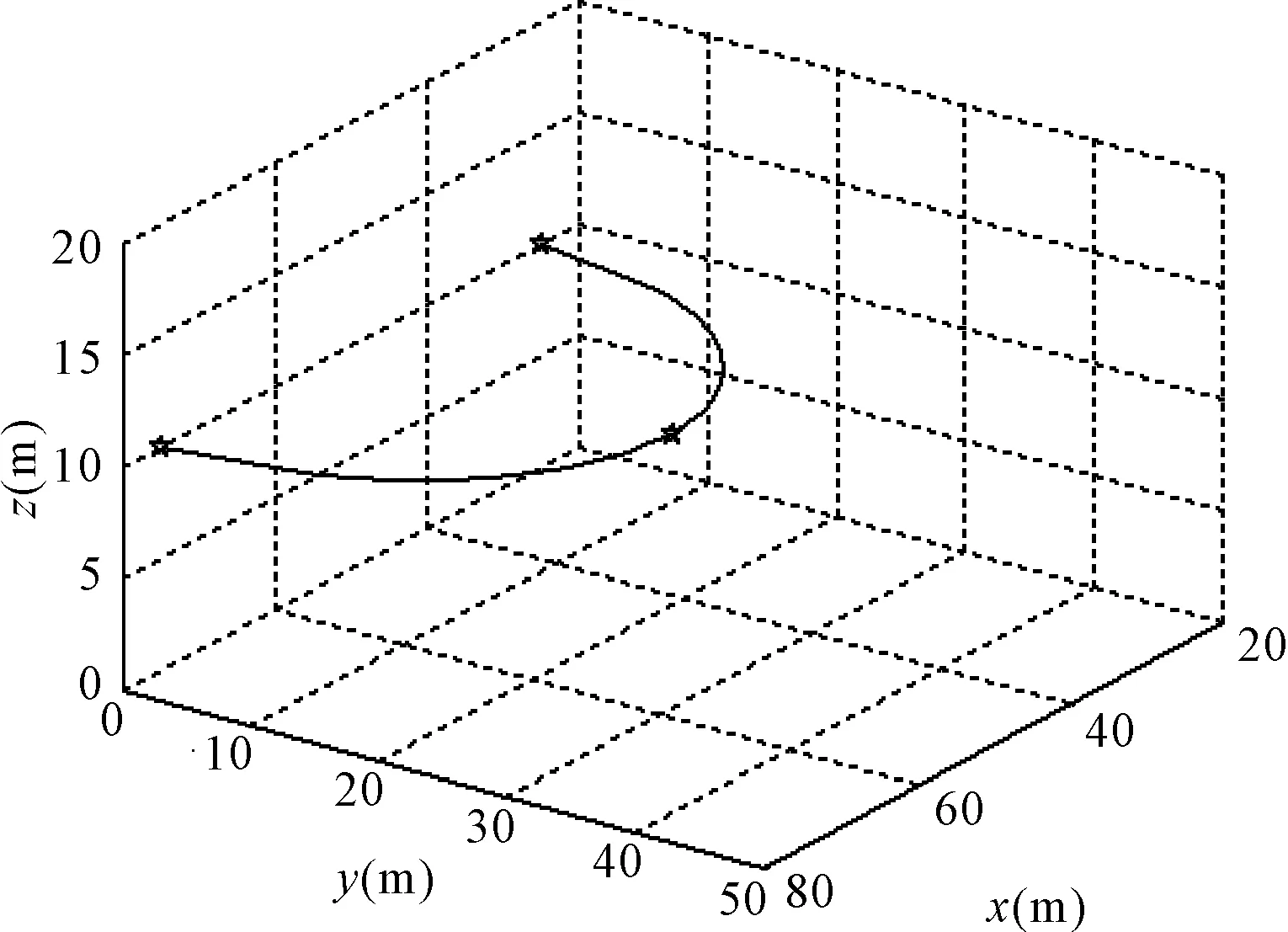
图6 圆弧轨迹曲线
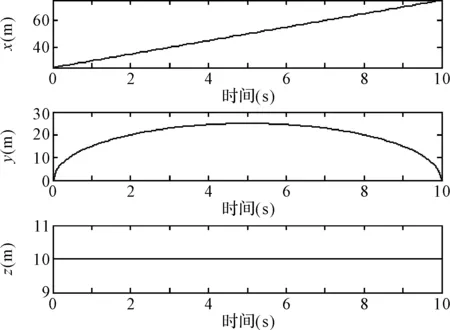
图7 坐标变化曲线
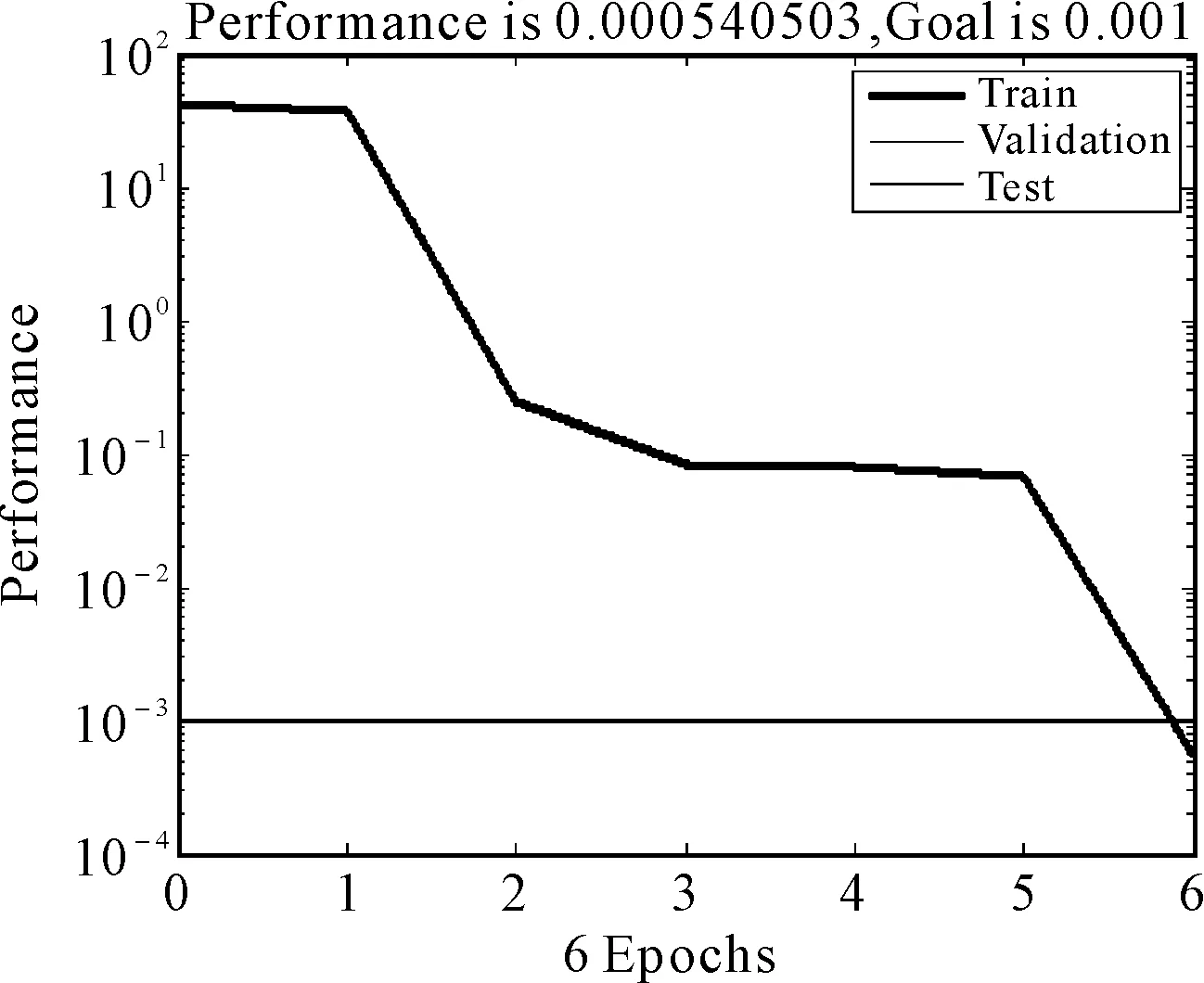
图8 误差性能曲线
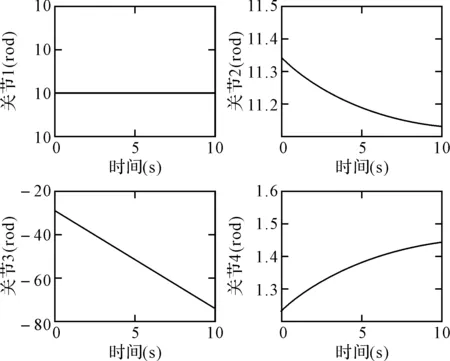
图9 关节变化曲线
从仿真图中看出,RBF神经网络拟合出的圆弧曲线过给定的三点,且确为半圆弧,轨迹光滑平顺;设定的误差,第五步就可达到要求精度,收敛速度快;各关节曲线光滑,没有转折点,变化平稳,不会出现剧烈颤抖。
6结语
圆弧轨迹规划是机器人控制系统中最基础的轨迹规划。为了克服笛卡尔空间圆弧插补算法收敛性和稳定性差,逼近效果不理想的问题,本文通过对工业四轴机器人运动学问题分析求解,建立其数学模型及三维模型;利用机器人末端圆弧经过的三点,用笛卡尔空间圆弧插补算法以及RBF神经网络对机器人末端圆弧轨迹进行规划并仿真。从轨迹仿真曲线的对比结果看出,RBF神经网络克服了插补算法稳定性差,拟合效果不理想的缺点,提高了收敛速度,所规划的圆弧轨迹平顺光滑,结果达到预期效果。
参 考 文 献
[1] [美]John J. Craig.机器人学导论[M].北京:机械工业出版社,2006:161-177.
John J. Craig. Introduction to Robotics[M]. Beijing: MechanicalIndustry Press,2006:161-177.
[2] 陈伟华,张铁.六自由度喷涂机器人插补算法的研究[J].微计算机信息,2009,25(8):251-252,263.
CHEN Weihua, ZHANG Tie. Six DOF Painting Robot interpolation algorithm[J]. Microcomputer Information,2009,25(8):251-252,263.
[3] 张政,邱钊鹏,诸刚.机器人技术[M].北京:机械工业出版社,2011:19-22.
ZHANG Zheng, QIU Zhaopeng, ZHU Gang. Robot technology[M]. Beijing: Mechanical Industry Press,2011:19-22.
[4] 殷际英,何广平.关节型机器人[M].北京:化学工业出版社,2003:26-28.
YIN Jiying, HE Guangping. Articulated robot[M]. Beijing: Chemical Industry Press,2003:26-28.
[5] 李双双.工业机器人建模、运动仿真与轨迹优化[D].呼和浩特:内蒙古大学硕士论文,2012.
LI Shaungshaung. Industrial robots modeling, motion simulation and trajectory optimization[D]. Hohhot: Inner Mongolia University Master Thesis,2012.
[6] 张志涌,等.掌握和精通MATLAB[M].北京:北京肮空航大大学出版社,1988,4:33-35.
ZHANG Zhiyong, et al. Control and proficiency in MATLAB[M]. Beijing: Beijing University Press,1988,4:33-35.
[7] 刘好民.6R关节型机器人轨迹规划算法研究及仿真[D].淄博:山东理工大学,2008.
LIU Haomin. 6R articulated robot trajectory planning algorithm and simulation[D]. Zibo: Shandong University of Technology,2008.
[8] 陈伟华.工业机器人笛卡尔空间轨迹规划的研究[D].广州:华南理工大学,2010.
CHEN Weihua. Industrial robot trajectory planning research in Cartesian space[D]. Guangzhou: South China University of Technology,2010.
[9] 陈伟华,招子安,吴少彬.六自由度机器人的圆弧轨迹规划算法研究[J].广州:华南理工大学,2013,35(11):4-5,14.
CHEN Weihua, ZHAO Zian, WU Shaobin. Six degrees of freedom robot circular path planning algorithm[J]. Guangzhou: South China University of Technology,2013,35(11):4-5,14.
[10] 扶宇阳.6R工业机器人结构设计及运动轨迹规划仿真研究[D].江门:五邑大学硕士论文,2013.
FU Yuyang. 6R industrial robot design and trajectory planning simulation research[D]. Jiangmen: Wuyi University Master’s Thesis,2013.
[11] 李东洁,邱江艳.一种机器人轨迹规划的优化算法[J].电机与控制学报,2009,13(1):123-127.
LI Dongjie, QIU Jianyan. A optimization of robot trajectory planning[J]. Motor and Control,2009,13(1):123-127.
[12] 赵娟娟.BP神经网络与RBF神经网络分析与研究[J].无线互联技术,2011,9:19.
ZHAO Juanjuan. BP neural network and RBF neural network analysis and research[J]. Wireless Internet Technology,2011,9:19.
[13] 苏美娟.径向基函数神经网络学习算法研究[D].兰州:兰州大学,2007.
SU Meijuan. RBF neural network learning algorithm[D]. Lanzhou: Lanzhou University,2007.
[14] 刘松国.六自由度串联机器人运动优化与轨迹跟踪控制研究[D].杭州:浙江大学,2009.
LIU Songguo. Six degrees of freedom serial robot Optimization and Tracking Control Research[D]. Hangzhou: Zhejiang University,2009.
[15] 陶智量.基于MATLAB的6自由度工业机器人仿真研究[D].长春:吉林大学硕士论文,2009.
TAO Zhiliang. 6 DOF industrial robot simulation research based on MATLAB[D]. Changchun: Jilin University Master’s Thesis,2009.
中图分类号TP18
DOI:10.3969/j.issn.1672-9722.2016.03.006
作者简介:辛大欣,男,硕士,副教授,研究方向:人工智能、计算机控制。刘少贞,女,硕士研究生,研究方向:计算机控制。
收稿日期:2015年9月10日,修回日期:2015年10月31日

