一种改进的竞争型蚁群算法在TSP问题中的应用*
张开碧 张洋川 万素波 白 银
(重庆邮电大学自动化学院 重庆 400065)
一种改进的竞争型蚁群算法在TSP问题中的应用*
张开碧张洋川万素波白银
(重庆邮电大学自动化学院重庆400065)
摘要路径优化问题在配送成本中是一个至关重要的因素。随着社会的不断进步和经济的快速发展,路径优化问题得到了大力发展,其中通过优化配送路径的方法可以大大节约运输成本从而对成本进行有效控制。在分析常规蚁群算法的基础上,采用竞争的方式让蚁群释放信息素来改变信息素的更新机制从而进一步优化配送路径。最终使整个算法收敛速度更快、搜索能力更强、精度更高,结果更优。
关键词蚁群算法; TSP; 信息素竞争机制; 路径优化
Application of An Improved Competitive Ant Colony Algorithm in TSP
ZHANG KaibiZHANG YangchuanWAN SuboBAI Yin
(College of Automation, Chongqing University of Posts and Telecommunications, Chongqing400065)
AbstractThe path optimization problem has been a crucial factor in the transportation costs. With the continuous progress of the society and the rapid development of economy, the path optimization problem has been greatly developed. The method of optimizing the distribution route can save the transportation costs and control the cost effectively. On the basis of analyzing the conventional ant colony algorithm, this way of competition is used to let the ant colony release information, and the pheromone update mechanism is changed to further optimize the distribution route. Finally, the result can be gotten that the algorithm converges faster, is more powerful and more accurate, and has better result.
Key Wordsant colony algorithm, TSP, pheromone competition mechanism, route optimization
Class NumberTP301
1引言
路径优化中最为典型的是旅行商问题(Traveling Saleman Problem,TSP)是最基本的路线问题。现在主流的路径优化算法有遗传算法、节约算法、粒子群算法和蚁群算法等[1~2]。其中比较重要的蚁群算法是一种仿生物智能算法,其模型是蚂蚁群体寻找食物的过程。它的鲁棒性较强,分布式特征使得算法可靠和全局搜索能力都比较强,同时也可以有效地和其他算法进行结合。但是也存在不足:搜索时间长,过快地收敛于局部最优解。为了解决上述问题,本文提出了一种改进的竞争型蚁群算法,更加有效地对路径进行控制以求得更优的路径结果,更大限度地节约成本。
2常规蚁群算法
2.1常规蚁群算法的基本原理
蚁群算法(Ant Colony Optimization,ACO)又称蚂蚁算法,是一种用来寻找优化路径的机率型算法。它由Marco Dorigo于1992年在博士论文中提出[3],其灵感来源于蚂蚁在寻找食物过程中发现路径的行为:蚁群在寻找食物时,它们总能找到一条从食物到巢穴之间的最短路径,并且能随环境变化而变化的搜索到新的最短路径。
蚁群是通过何种方式寻找到最优路径的呢?其实,蚂蚁在寻找食物时,能在其走过的路上释放一种特殊的分泌物—信息素,而且信息素会随着时间的推移而逐渐挥发。蚂蚁在选择该路径的概率与当时这条路径上信息素的强度成正比。某条路径上通过的蚂蚁越来越多,其留下的信息素浓度就越来越高,后面的蚂蚁选择这条路径的概率也就越来越大,将会进一步增加该路径的信息素强度,吸引更多的蚂蚁,从而形成一种正反馈机制[4]。蚁群正反馈机制如图1所示,刚开始时,各条路径上的信息素相同,30只蚂蚁等概率地选择下一个节点,A-C-B和A-D-B上的蚂蚁都是15只。但是蚂蚁通过较短路径的时间会更短,那么在单位时间内,通过较短路径的蚂蚁就越多,留下的信息素越多,信息素越大,那么这条路径被选择的概率也就越大,就会被更多的蚂蚁所选择[5]。图中A-C-B的距离小于A-D-B,所以经过一段时间后,A-C-B上的蚂蚁逐渐增加到20,A-D-B减少到10。由于这种正反馈机制的持续作用,将会有更多的蚂蚁选择A-C-B这条较短的路径,蚁群最终就找到了它们的最佳觅食路径。

图1 蚁群正反馈机制
目前,人们已经从蚁群的这种觅食过程中总结出了一些基本的规则[6]。在TSP问题中,蚂蚁一开始被随机放置到各个节点,每个节点只能被访问一次,在每一步的路径构建中,蚂蚁k按照概率选择下一个访问节点。例如,蚂蚁k在节点i选择节点j作为下一个访问点的概率为
(1)
式(1)中τij代表(i,j)上的信息素浓度,ηij=1/dij代表一个最初给定的启发式信息,dij代表i~j的距离,α和β这两个参数表示信息素和启发式信息的相对影响力,allowedk代表一个集合,这个集合包含了那些还可以被访问的所有节点。所以在这种选择规则下,路径(i,j)的选择概率就由信息素τij和启发式信息ηij的大小共同决定。
(i,j)上的信息素τij(t)的更新方程为
τij(t)=(1-ρ)τij(t-1)+Δτij
(2)
(3)
(4)
式(2)~式(4)共同决定(i,j)路径上信息素的更新。式(2)中参数ρ表示信息素的挥发系数(0<ρ<1),τij(t-1)表示上次搜索后(i,j)上的信息素,Δτij表示当前这次搜索过程中,蚁群释放的信息素。式(3)表示第k只蚂蚁会经过(i,j),Lk表示第k只蚂蚁的搜索路径,第k只蚂蚁在(i,j)上的信息素增量为Q/Lc,Q为信息素增加系数,Lc为此次搜索的最优解,即蚁群此次搜索到的最短路径。式(4)表示此次搜索后,i~j上增加的信息素等于所有由i~j的蚂蚁释放的信息素相加。
2.2用常规蚁群算法来求解TSP问题
TSP问题是数学领域中著名的N-P问题。假设有一个旅行商人要访问n个城市,但是他所访问城市要满足一定要求,每个城市只能访问一次;从一个城市出发,在访问完其他城市后,最后回到开始的那个城市。目标路径为经过所有n个城市路径距离最小的那一条路径。
用蚁群算法求解TSP问题的步骤如下[7~8]:
1) 变量初始化;
2) 蚂蚁构造路径,按概率选择路径,每只蚂蚁完成各自的周游;
3) 计算本次搜索的最佳路线;
4) 信息素的更新;
5) 禁忌表清零;
6) 判断是否达到最大搜索次数?如果未达到最大搜索次数,跳入步骤2),如果达到最大搜索次数,输出结果。
TSP问题的本质是求满足要求的最短路径,即给定一个带权图G=(N,d),其中N是图中的各个节点的集合,d是各个节点之间连线的集合。
TSP问题的求解模型为
(5)
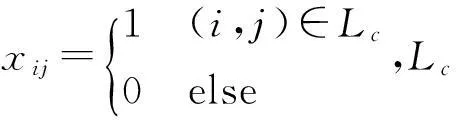
约束条件公式:
(6)
式(6)中,约束(a)表示路径只能从一条边出,约束(b)表示路径只能从一条边进,约束(c)表示回路中不含任何子回路,满足以上三个约束条件的解就构成了一条Hamilton回路[9]。
蚁群算法在TSP问题中取得了不错的效果,但是也存在以下不足之处:
1) 参数设置得不准确,就会导致求解速度慢且所得解质量不高;
2) 常规蚁群算法计算量大,信息素更新容易求得局部最优解,从而造成算法停滞;
3) 常规蚁群算法从理论上要求所有蚂蚁在最后都选择最短那条路径,但实际上是不可能的,因为算法在一定的搜索次数内可能无法找到最优解。
为了提高算法的合理性和精确性,本文对常规蚁群算法做出了一些改进。
3改进的蚁群算法
通过以往学者在TSP问题对蚁群算法做出的研究,可以将蚁群算法做出以下几个方面的改进[10]:
1) 选择概率中各个参数的设置;
2) 改变信息素的更新规则;
3) 与其他优秀算法相结合。
改进的主要目标如下:
1) 提高搜索结果的精确性,加快收敛速度的同时避免过早的局部收敛,从而避免算法过早停滞。
2) 加强算法的自我搜索能力。
本文提出的改进蚁群算法中,主要是更改了信息素的跟新规则。并不是所有蚂蚁在每次搜索结束后都进行信息素更新,而是只对每次搜索到最短路径的那只蚂蚁的信息素进行更新。
改进蚁群算法的信息素更新规则如式(7)~式(10):
(7)
(8)
τij(t)=(1-ρ)τij(t-1)+ρΔτij
(9)
τij(t)∈[τmin,τmax]
(10)
信息素挥发系数ρ体现了路径上信息素的保留能力,在常规蚁群算法中,信息素挥发系数ρ为一个常系数,但是这样会导致算法在初始阶段寻优能力不足,得到较优化结果的同时陷入局部最优导致算法停滞,所以在改进的蚁群算法中将信息素挥发系数与搜索次数相结合,随着搜索次数的增加,信息素挥发系数也发生改变。从式(7)可以看到,改进蚁群算法在搜索前期采用较小的挥发系数,中后期加大挥发系数,这种随搜索次数变化的信息素挥发系数有助于加强算法在前期的搜索能力,也能避免算法在中后期的停滞。
在常规蚁群算法中,知道路径(i,j)上的信息素增量为蚁群中所有从i~j的蚂蚁释放的信息素相加,但是经过(i,j)的大部分蚂蚁,它们的周游路径并不是最优值,这就会对后面的搜索产生一定的干扰。而在改进蚁群算法中,每次搜索完成后,蚁群通过竞争的方式来释放信息素。
竞争规则如下:
1) 每次搜索完成后,有且仅有一只蚂蚁能释放信息素;
2) 释放信息素的蚂蚁必须是当前这次搜索中的最优蚂蚁;
3) 如果当前这次搜索中的这只最优蚂蚁寻得的路径比前一次搜索的最优蚂蚁寻得的路径更短,将释放大小为1/Lc的信息素,Lc为蚂蚁寻得路径的距离;
4) 如果当前这次搜索中的这只最优蚂蚁寻得的路径和前一次搜索的最优蚂蚁寻得的路径相同,将释放大小为1/Nc-maxLc的信息素,Nc-max为总的搜索次数;
5) 如果当前这次搜索中的这只最优蚂蚁寻得的路径比上一次搜索的最优蚂蚁寻得的路径更长,将不会释放信息素。
根据这种新的竞争规则可以看出,能够释放信息素的蚂蚁会经历两次筛选,第一次与本次搜索中的其他蚂蚁进行比较,第二次则是与前一次搜索的最优蚂蚁进行比较。而且寻得路径越短的蚂蚁,能释放更多的信息素,按照这样的规则,一直循环下去,能够有效地保留那些优秀蚂蚁,淘汰那些结果不够优化的蚂蚁,这样大大地提高了蚁群搜寻结果的精确性。
从式(9)可以知道,与常规蚁群算法不同的是,改进蚁群算法中不论上一次搜索后保留的信息素,还是当前这次搜索后释放的信息素都跟信息素挥发系数ρ相关,这样就大大加强了算法的搜索能力,避免了算法因找到局部最优解而导致停滞的可能。
式(10)作为信息素限制条件,主要是为了防止某条路径上的信息素表现过大或过小的情况[11]。通过这种方法可以有效控制信息素,避免信息素超过最大值或小于最小值,以此提高算法的有效性。
4改进蚁群算法的应用
本文用改进的蚁群算法和常规蚁群算法同时对TSP问题进行了求解,并对比和分析了改进的新算法的优点。
设定20个节点坐标:(5,5)、(25,12)、(8,23)、(11,8)、(30,2)、(21,4)、(20,20)、(8,10)、(3,13)、(30,9)、(25,26)、(15,16)、(20,6)、(33,10)、(23,0)、(0,17)、(36,3)、(18,23)、(34,15)、(28,14)。
下面是常规蚁群算法和改进蚁群算法的结果。其中常规蚁群算法的结果如图2,改进蚁群算法的结果如图3。
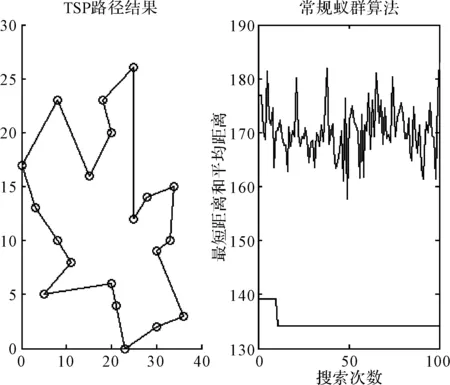
图2 常规蚁群算法结果
从实验图形结果中可以看出,改进蚁群算法的最短路径距离为130.007,常规蚁群算法的最短路径距离为134.283,改进蚁群算法的结果明显更加精确。对比图2和图3,常规蚁群算法的搜索次数少,收敛速度过快,还无法找到最短路径,而改进蚁群算法则是一次一次的优化去搜索最短路径,说明改进蚁群算法寻找最优解的能力加强了。而且改进蚁群算法中,每次搜索后,蚁群搜索路径的平均值也是逐渐变小的,说明新的信息素更新机制效果十分明显。

图3 改进蚁群算法结果
5结语
本文首先介绍了常规蚁群算法的原理和对TSP问题的求解方法,发现了常规蚁群算法存在的不足,然后通过改进信息素更新机制,加强算法的自我搜索能力,避免局部收敛过早。最后通过实验,将常规蚁群算法和改进蚁群算法进行了对比,证明了改进蚁群算法能提高精确度,加强自我搜索能力。
参 考 文 献
[1] 朱献文,李福荣.求解旅行商问题的几种智能算法[J].计算机与数字工程,2010,38(1):32-35.
ZHU Xianwen, LI Furong. Several intelligent algorithms for solving traveling salesman problem[J]. Computer and Digital Engineering,2010,38(1):32-35.
[2] 李擎,张超.一种基于粒子群参数优化的改进蚁群算法[J].控制与决策,2013,28(6):873-878.
LI Qing, ZHANG Chao. An improved ant colony algorithm based on particle swarm optimization[J]. Control and Decision,2013,28(6):873-878.
[3] Dorigo M, Maniezzo V. Ant system: Optimization by a colony cooperating Agents[J]. IEEE Transactions on Systems, Man and Cybernetics part B,1996,26(1):29-41.
[4] WANG L, ZHU Q. An efficient approach for solving TSP: the rapidly Convergen-t ant colony algorithm[C]//Fourth International Conference on Natural Computation, IEEE,2008,186(4):448-452.
[5] 吴华锋,陈信强.基于自然选择策略的蚁群算法求解TSP问题[J].通信学报,2013,34(4):165-170.
WU Huafeng, CHEN Xinqiang. Ant colony algorithm based on natural selection strategy to solve[J]. Problem TSP Journal of Communication,2013,34(4):165-170.
[6] 段爱民,陈泽琳.基于改进蚁群算法的物流配送路径优化[J].计算机技术与发展,2011,21(12):178-181.
DUAN Aimin, CHEN Zelin. Optimization of logistics distribution routing based on improved ant colony algorithm[J]. Computer Technology and Development,2011,21(12):178-181.
[7] 杨再甫,黄友锐.TSP的改进蚁群算法求解及其仿真研究[J].合肥工业大学学报,2014,37(8):928-932.
YANG Zaifu, HUANG Yourui. The improved ant colony algorithm for TSP and its simulation[J]. Journal of Hefei University of Technology,2014,37(8):928-932.
[8] 张伟娟,张红梅.基于蚁群算法的基因路径预测[J].计算机系统应用,2015,24(3):280-283.
ZHANG Weijuan, ZHANG Hongmei. Genetic algorithm based on ant colony algorithm to predict the[J]. Computer System Applications,2015,24(3):280-283.
[9] 柳寅,马良.模糊蚁群算法及其在TSP中的应用[J].数学的实践与认识,2011,41(6):150-154.
LIU Yin, MA Liang. Fuzzy ant colony algorithm and its application in TSP[J]. Practice and Cognition of Mathematics,2011,41(6):150-154.
[10] Valdez F, Chaparro I. Ant Colony Optimization for solving the TSP symmetric with parallel processing[C]//IFSA World Congress and NAFIPS Annual Meeting(IFSA/NAFIPS),2013:1192-1196.
[11] 姚艳.一种最大最小蚂蚁系统的改进算法[J].数学的实践与认识,2014,44(15):242-247.
YAO Yan. An improved algorithm for the maximum and minimum ant system[J]. Practice and Cognition of Mathematics,2014,44(15):242-247.
中图分类号TP301
DOI:10.3969/j.issn.1672-9722.2016.03.003
作者简介:张开碧,女,硕士,副教授,研究方向:人工智能、数据采集。张洋川,男,硕士研究生,研究方向:路径优化、人工智能。
收稿日期:2015年9月4日,修回日期:2015年10月26日

