慢教育语境下数学逆商的培养
摘 要 鉴于数学逆商对人的发展的正向价值和积极意义,数学慢教育课题组对数学逆商的培养框架进行理性建构和知性研究。其包括思维控制力、思维归属力、思维影响力、思维延伸力四个维度和认知心向、数学观念以及课程精神三个层面。
关键词 慢教育语境 数学逆商 教育价值
就课程教育哲学观而言,研究逆商培养的课题是数学慢教育的使命和责任,具有前沿教育的人性意义。[1]逆商AQ(Adversity Quotient)又称挫折商,是美国职业培训师保罗·斯托茨提出的生存学概念,原意是指人们面对挫折、摆脱困境和超越困难的能力。数学逆商则是指一个人对数学学习过程中所遇困难和挫折的应对智力及应变能力。[2]数学慢教育课堂的数学逆商特指数学认知理解中,面对“学不会和不会学”“做不会和不会做”等事实性困难,能够以积极的心态,想办法把握数学概念的内驱力和素养力。
数学逆商包括四个方面:一是数学控制,是指个体对数学学习中所遇逆境的控制能力;二是数学归属,是指个体认识到数学学习逆境产生的原因及愿意承担责任、改善后果的能力;三是数学影响,是指个体对数学学习中逆境影响的评估与察觉能力;四是数学延伸,是指数学学习逆境对个体的持续影响时间。[3]
数学慢教育课堂的本质特征就是让学生的数学思维过程“看得见”。[4]而“看得见”是认知理解到达“知其然且知其所以然”境界的外在表现,其本身就带有“山重水复”与“柳暗花明”对立统一的“挫折感”色彩,所以它具有提高思维逆商水平的功能。慢教育语境下的逆商培养主要体现在“形而上”的思维科学层面,包括思维控制力(基本问题)、思维归属力(基本套路)、思维影响力(基本思想)和思维延伸力(基本经验)。鉴于数学逆商对人的发展的教育价值和指导意义,数学慢教育课题组对数学逆商的培养框架进行理性建构和知性研究。
一、慢教育课堂数学逆商的教育价值
“初中生数学逆商量表”的第二部分是数学逆商测试题,包括数学控制、数学归属、数学影响、数学延伸四个维度。每个维度5个题目,共20道题,采取5点计分法,得分越高表示数学逆商越高。90~100分之间,表明有能力克服大部分学习困难;70~89分之间,表示能克服部分学习困难;50~69分之间,表示能克服少部分学习困难;50分以下,显示为逃避学习困难状态。[5]就数据观下的数学逆商与数学思维力正相关的论断来看,数学逆商教育的宏观价值在于生活品质的提高,其微观价值在于数学学习力的提升,其内在力量在于强大的心向状态(先于一定活动而又指向该活动的一种动力准备状态)。因此,研究数学逆商教育的培养意义在于认知心向、数学观念和课程精神三个维度。
1.数学逆商教育的内在力量 —— 一种积极的认知心向
“内在力量”属于心理学范畴名词,常常与认知心向具有相关一致性。积极的认知心向能够促进后续同类问题的解决,此时内在力量表现在积极寻求问题解决的思想行为上;消极的认知心向会阻碍先前经验对后续相似问题的支配作用,具体表现在个体经验在头脑中处于惰性状态而无迁移发生。这是学科教育必须直面且不容回避的心理倾向问题,也给数学逆商教育指明了学科方向。
数学逆商在认知心理学领域表现出两种倾向:一是尝试错误的积极心理,能够把错误资源转化为可利用的再学习资源,这是一种积极的认知心向;二是回避错误的消极心理,把“不会学”“不会做”当成“学不会”和“做不会”的内在根据,这是一种带有惰性特征的认知心向。数学慢教育课堂数学逆商的内在力量就是变消极为积极、变惰性为活性的认知心向。主要行为方式就是让思维过程说话、思维方法外显、思维表征立体,终归于数学概念的二次理解(错误→正确)和三次把握(不平衡→平衡→不平衡)。
2.数学逆商教育的宏观价值 —— 一种生态的数学观念
在社会科学中,我们通常把从大的方面、整体方面去研究把握科学的方法叫做宏观法。遵循宏观方法概念的逻辑顺序,我们把逆商教育理解为数学习惯和数学学习适应论。在这样的数学观念下,我们必须把课堂挫折感作为评价有效教学的一个关键指标。为此,课堂数学问题预设难易梯度比定位是7∶2∶1。这样才能让学生在适度的挫折感中养成冷静从容的思维品质。而思维冷静、心理从容的人生状态是数学教育在塑造人性层面的终极追求,是一种宏观价值取向,反射出一种生态数学观念。
数学逆商教育的宏观价值来源于自然界,并随着人类的进化而进化,随着社会的发展而发展。宏观价值的终极本源只能是运动着的物质世界和劳动着的人类社会。逆商教育作为物质世界的一种教育形态,则表现为耐挫心理能力;把其作为人类社会的一种教育心理状态,则表现为抗挫能力水平。数学慢教育语境下逆商教育的宏观价值是学生积极挑战错误,自觉应答困难的数学观念,终归于任意的物质形态数学力。
3.数学逆商教育的微观价值 —— 一种科学的课程精神
在概念域范围内,通常把从小的方面、局部方面去研究把握科学的方法叫做微观方法。遵循微观方法概念的逻辑内涵,我们把逆商教育的微观价值理解为三个思想层次:一是“前双基”(基础知识和基本技能)学习需要在试错、悟错、改错的挫折中习得智慧,并以此为发现、提出问题(后两能)铺垫智慧基础;二是“后双基”需要在反复修正错觉、错法、错识中锤炼认知方法体系的可辨性,这能为分析、解决问题(前两能)提供“基本套路”;三是“前后双基”内部联系需要在建构中、比较中、批判中建立和完善,能为知识结构教育转化为认知结构教育提供逻辑判断。而培养“四基”“四能”是课程教育的精神宗旨。因此,逆商教育就微观教学论价值来说,带有明显的科学课程精神。
科学性与艺术性是教学的两种基本属性。[6]教学科学主义确实给教学提供了规范的可操作性的指导。就课程教育的科学性来说,逆商教育是课程教育的首要目标,为社会塑造“大写的人”,为适应各种挫折现象提供生存力层面的能力帮助,具有“久病成医”的意义。
二、慢教育课堂数学逆商的培养框架
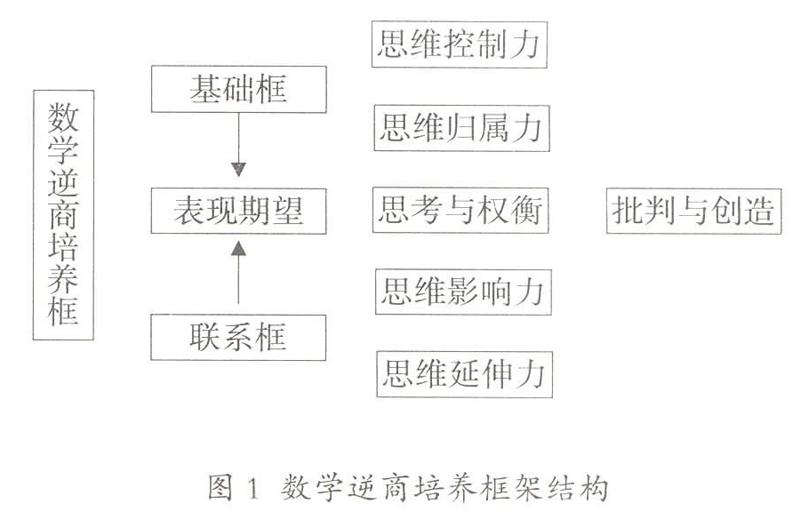
美国的《新一代学科教育标准》(the Generation Science Standards ,NGSS)包括“表现期望”(Performance Expectantion)、“基础框”(Foundation Boxes)、“联系框”(Connection Boxes)三个层次,其中后两者是为了达到“表现期望”而展开的。[7]数学慢教育课堂数学逆商教育培养框架也具有三个层次的本质意义(见图1)。表现期望是思维控制力、归属力、影响力以及延伸力等系统思维内部相互作用的结果,是逆商教育水平得以提高的具体表现。
1.思维控制力的培养
慢教育课堂数学逆商培养语境下,教之道在于“度”,学之道在于“悟”。[8]通过对“基本问题”的二次数学或多次数学,延长概念生长期,给学生“做”“悟”“思”“辨”的时间,使得思维控制力聚焦核心概念。而思维控制形态集中聚焦的过程就是数学逆商增强的心理过程,学生的思维形态表现出“学习进阶”的倾向。
在学习“莱洛三角形与圆”主题知识时,我们遵循多次数学原理,采用“情景→定义→操作→发现”的思维线索,在比较思想的统摄下,落实“基本问题”(莱洛三角形的概念:分别以等边三角形的三个顶点为圆心、边长为半径画弧,这三段弧围成的图形,叫做莱洛三角形)多次研究的思维模式(识别、画图、运动、比较等)。使得莱洛三角形的个性特征(在直线上滚动一周,其中心轨迹跳跃3次)和公共特性(可以作为下水道的盖子、汪克尔发动机的转子)得以通透敞亮,进而延长习得概念的历程,丰富了学生认知理解的表象。为此,个体数学逆商的表现形态得以多感官体验。
2.思维归属力的培养
研究数学问题是有“基本套路”的,举一反三是思维归属力得以内驱的外在表现。“反三”“通百”这些行为动词本身带有逆商教育倾向的培养意义,即通过正反例证伴随着质疑行为达成类化和内化的认知目标。而内化概念的过程就是数学认知理解由不确定到确定的过程,包括还原主题概念原本样态的过程。数学慢教育心理环境下,培养数学逆商就是以探寻基本套路为动机的方法形态行为。
在学习“最小覆盖圆”这一新概念时,我们首先给出概念的共性特征:把能覆盖平面图形的最小的圆称为该平面图形的最小覆盖圆。其次让学生自主探索“覆盖线段→覆盖三角形→覆盖四边形的最小覆盖圆。最后让学生在证实发现和表征规律的过程中习得切身理解的主概念(锐角三角形的最小覆盖圆就是其外接圆、直角三角形和钝角三角形的最小覆盖圆就是以最长边为直径的圆)。遵循这样的饱含挫折感的逻辑认知顺序,能让学生经历概念生长的全过程,既知其然,更知其所以然,终于新概念的完备生长。
3.思维影响力的培养
哈肯(H.Haken)认为,从组织的进化形式来看,如果不存在外部命令,系统按照相互默契的某种规则,各尽其责而又协调地自动地形成有序结构,就是自组织。[9]这里的“外部命令”“某种规则”“有序结构”都是思维影响力发挥作用的物质基础,包括主客观精神实体,是基本思想得以渗透的本质外显。数学学习的本质不在于做多少题,而在于思想体系的建立。个体认知体系建立的过程就是坚守数学逆商信念的过程,因为思想体系包含思维系统各要素间的作用与反作用。学无定法,不法而法,联系即法,这是数学慢教育语境思维影响力的本质特征,是培养数学逆商目标的内部力量。
初中学生抽象思维能力偏弱,理解“菱形的判定方法”困难。慢教育语境课堂秉持让学生“做菱形”的思想,在几何直观思想反射下,经历由“剪菱形→叠菱形→折菱形”做数学的行为,伴随证实与推演的迂回曲折的逻辑联系过程,终于数学逆商能力的上升和抽象思维倾向的过渡与建设,落实课程教育哲学联系观。
4.思维延伸力的培养
德国教育家克里克、施莱尔马赫(Friedrich Schleiermacher)和奥康纳都认为教育学更多地基于经验而不是理论。[10]经验是思维延伸力的内在冲动和外在冲突。《义务教育数学课程标准(2011年版)》也把“积累活动经验”作为提高学生数学素养的法定标准,是数学课程教育的重要目标之一。因此,就教育政策、专家立言抑或是经验行为都渗透逆商教育的本体意义。数学慢教育是以数学逆商教育为主流文化特征的过程行为,着力打造让学生的思维过程“看得见”工程,立体延伸认知思维的长、高、宽。
我们做“探索等积矩形中的函数关系”这一实验,目的就是为理解“反比例函数概念”提供先行组织经验。首先在学具箱内准备面积为24的不同矩形纸片若干张(注:把1×24与24×1看成不同类型的纸片),让学生猜想并证实其边长。然后让学生以长和宽为有序“实数对”,在平面直角坐标系内描点并写出函数关系式。最后让学生把边长为整数单位的矩形纸片(24×1,12×2,8×3,6×4,4×6,3×8,2×12,1×24)按照数序列放置在坐标系内,再将右上角顶点用平滑的曲线连接起来,并表述其共性特征。这种以经验为联系的“前概念”行为,既建立了核心概念的表像,又实现概念的可辨形态,终于概念的延伸力。
参考文献
[1] 朱桂凤,孙朝仁.数学慢教育研究综述[J].江苏教育研究,2013(7A).
[2] 曹春艳,张定超.初中生数学逆商的调查与分析[J].数学教育学报,2014(2).
[3] 曹春艳,张定超,丁亥复赛.民族地区初中生数学逆商的调查与分析——以甘南藏族自治州藏汉初中生数学逆商的比较研究[J].数学教育学报,2015(2).
[4] 范存丽.让数学思维过程“看得见”[J].人民教育,2014(15).
[5] Paul G S. Adversity Quotient: Turning Obstacles into Opportunities [M]. John Wiley and Sons,Inc,1997.
[6] 罗增儒.教学既是科学又是艺术[J].中学数学教学参考(上旬),2015(8).
[7] 王宝艳,冯永刚.美国《新一代科学教育标准》探析[J].数学教育学刊,2015(4).
[8] 章建跃.数学学习与智慧发展(续)[J].中学数学教学参考(上旬),2015(8).
[9] H 哈肯.协同学——自然成功的奥秘[M].戴鸣钟,译.上海:上海科学普及出版社,1988.
[10] 苏景春,宫盛花.系统科学视角下的教育学探析[J].课程·教材·教法,2015(6).
【责任编辑 郭振玲】

