Numerical simulation of seismic damage and cracking of concrete slabs of high concrete face rockfill dams

*

aCollege of Water Conservancy and Hydropower Engineering,Hohai University,Nanjing 210098,China

bKey Laboratory of Failure Mechanism and Safety Control Techniques of Earth-rock Dam of the Ministry of Water Resources,Nanjing 210024,China

cChangjiang Institute of Survey,Planning,Design,and Research,Wuhan 430010,China

Numerical simulation of seismic damage and cracking of concrete slabs of high concrete face rockfill dams

Wei-jun Cena,b,*,Lang-sheng Wena,Zi-qi Zhanga,Kun Xiongc

aCollege of Water Conservancy and Hydropower Engineering,Hohai University,Nanjing 210098,China

bKey Laboratory of Failure Mechanism and Safety Control Techniques of Earth-rock Dam of the Ministry of Water Resources,Nanjing 210024,China

cChangjiang Institute of Survey,Planning,Design,and Research,Wuhan 430010,China

Available online 20 September 2016

Based on the damage constitutive model for concrete,the Weibull distribution function was used to characterize the random distribution of the mechanical properties of materials by f i nely subdividing concrete slab elements,and a concrete random mesoscopic damage model was established.The seismic response of a 100-m high concrete face rockfill dam(CFRD),subjected to ground motion with different intensities,was simulated with the three-dimensional finite element method(FEM),with emphasis on exploration of damage and the cracking process of concrete slabs during earthquakes as well as analysis of dynamic damage and cracking characteristics during strong earthquakes.The calculated results show that the number of damaged and cracking elements on concrete slabs grows with the duration of earthquakes.With increasing earthquake intensity,the damaged zone and cracking zone on concrete slabs grow wider.During a 7.0-magnitude earthquake,the stress level of concrete slabs is low for the CFRD,and there is almost no damage or slight damage to the slabs.While during a 9.0-magnitude strong earthquake,the percentages of damaged elements and macrocracking elements continuously ascend with the duration of the earthquake,peaking at approximately 26%and 5%at the end of the earthquake,respectively.The concrete random mesoscopic damage model can depict the entire process of sprouting,growing,connecting,and expanding of cracks on a concrete slab during earthquakes.

Concrete face rockfill dam;Random mesoscopic damage model;Seismic response;Dynamic damage to concrete slab;Macrocracking;Numerical simulation

1.Introduction

Due to adoption of layered filling and thin layer vibration compaction technology,modern concrete face rockfill dams (CFRDs),which are very safe and adaptable to topographical and geological conditions,have become one of the main candidate types for high dams.In the last three decades, CFRDs have been rapidly developed in China,with more than 270 dams constructed or under construction,72 of which are over 100 m in height.

China is located between the circum-Pacif i c seismic belt and the Mediterranean-Himalayan seismic belt,and is an earthquake-prone country.Many CFRDs are located in regions of high earthquake intensity(Chen et al.,2011,2013).On May 12,2008,the 156-m high Zipingpu CFRD,in southwestern China,suffered a strong earthquake with a Richter magnitude scale of 8.0.The main dam body remained safe on the whole, but extrusion and uplift failures of various degrees along the upper horizontal construction joints and crushing damagenear the middle vertical joints in the concrete slabs occurred (Kong et al.,2011;Wieland,2009;Xu et al.,2015;Zhang et al., 2015a).The structural integrity of concrete slabs under various loads is the key to ensuring the safety of seepage control of CFRDs.In conventional structural analysis of CFRDs,linear or nonlinear elastic models are often used to analyze the stress and deformation of concrete slabs.The possible cracking zone on slabs is determined according to the calculated principal tensile stress,which cannot ref l ect the entire evolution process of sprouting,growing,expanding,and the f i nal state of slab cracks (Arici,2011;Wang et al.,2014).Classical fracture mechanics mainly focuses on the strength problem of structures with cracks and the patterns of crack development.However,the process of damage and cracking of concrete slabs,including mesocrack initiation and the formation and evolution of macrocracks,is complex,and classical fracture mechanics cannot describe the generation of initial mesocracks before the formation of macrocracks.Damage theory,meanwhile,can be employed to study the entire evolution process of the mechanical properties of concrete slabs from mesocrack initiation to fi nal failure under the effect of external loads(Xiong et al., 2013,2014).Over the last decade,a series of concrete mesomechanical damage models have been put forward in China and abroad,including the lattice model(Schlangen and Garboczi,1997),random particle model(Bazant and Tabbara, 1990),micromechanicalmodel(MohamedandHansen, 1999),and random mechanical characteristic model(Tang and Zhu,2003).Owing to the limitation of computational capacity,most of the meso-mechanical damage models have only been used in numerical simulation of a single concrete member or a simple structure,and cannot be used to analyze the mesoscopic damage and macrocracking of entire concrete dams or other complex concrete structures.However,the random mechanical characteristic model has been employed frequently in static and dynamic simulation of failures of concrete or hardfill dams(Huangetal.,2008;Zhongetal.,2009;Xiongetal.,2013, 2014).Zhong et al.(2009)thought that it was impossible to analyze the damage and cracking of concrete dams in a strict mesoscale,while the random mechanical characteristic model, which considers the inf l uence of inhomogeneity in the mesoview based on the assumption of macroscopic homogeneity,is an effective way to simulate the seismic damage to a concrete arch dam.The ultimate failure patterns calculated with this method were consistent with those from laboratory tests in seismic damage analysis of a high arch dam(Zhong et al., 2009).

In this study,the idea described above was adopted to analyze the cracking process of concrete slabs in a typical 100-m high CFRD.A f i ne secondary subdivision of initial concrete slab elements was conducted first,and then the concrete random mechanical analysis method and damage constitutive model were combined to simulate the dynamic damage and cracking of concrete slabs.Seismic response analysis of the CFRD was carried out using the threedimensional finite element method,focusing on predicting the damage and cracking characteristics of concrete slabs during earthquakes with different intensities.

2.Damage constitutive model for concrete

The damage constitutive relationship for concrete under uniaxial stress can be expressed as

where σ is the stress,ε is the strain,D is the damage variable, and E0is the initial elastic modulus of concrete without damage.

The damage to each concrete slab element may be tensile or compressive damage according to the maximum tensile strain criterion or Mohr-Coulomb criterion,respectively.Fig.1 shows the tensile and compressive damage constitutive relationships for concrete adopted in this study.Each element on the concrete slab shows elastic properties in the initial stage, and its stress grows with the increasing load.When the stress or strain approaches a critical value determined by the damage criteria,damage to the element or even complete destruction of the element occurs.

In Fig.1(a),σtis the tensile stress;εtis the tensile strain;ft0is the uniaxial tensile strength;εt0is the tensile strain corresponding to ft0;and εtuis the ultimate tensile strain,εtu=ξεt0, where ξ is the coeff i cient of ultimate tensile strain.In the uniaxial tensile state,the maximum tensile strain criterion is used to determine whether the tensile damage occurs.When the tensile strain reaches εt0,damage to the element occurs; when the elementtensile strain reachesεtu,complete destruction occurs,with the damage variable Dtin the uniaxial tensile state equal to 1,which means that macrocracks appear.

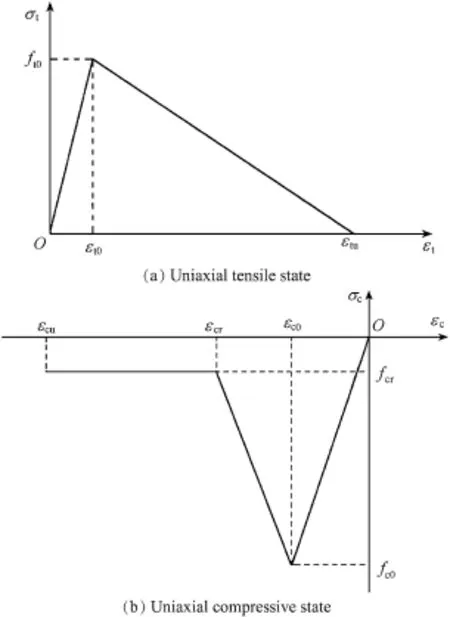
Fig.1.Damage constitutive relationships for concrete.

The damage variable Dtin the uniaxial tensile state is as follows:

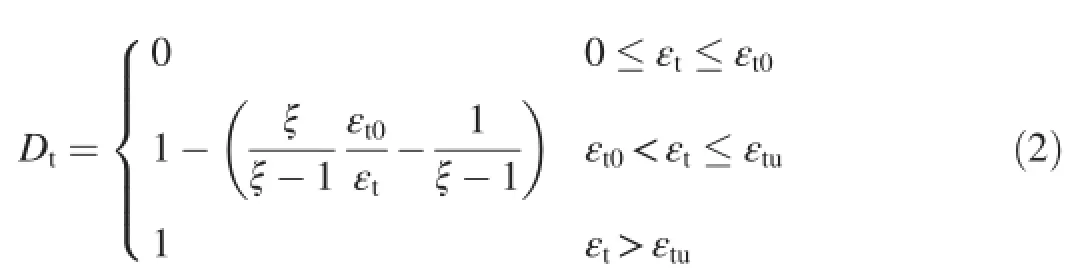
where ε1,ε2,and ε3are the first,second,and third principal strains,respectively,and each of them is taken as zero when the values are smaller than zero.

When an element is in a compressive or shear state,the Mohr-Coulomb criterion isused to determinewhether the compressive(shear)damage occurs.In Fig.1(b),σcis the compressive stress,εcis the compressive strain,fc0is the uniaxial compressive strength,and εc0is the corresponding compressive strain.When the compressive strain reaches εc0, damage to the element occurs.fcris the residual compressive strength,fcr=λfc0,where λ is the coeff i cient of residual compressive strength;εcris the compressive strain corresponding to fcr,εcr=rεc0,where r is the coeff i cient of residual compressive strain;and εcuis the ultimate compressive strain, εcu=ζεc0,where ζ is the coeff i cient of ultimate compressive strain.When the element compressive strain reaches εcu, complete destruction occurs.

The damage variable Dcin the uniaxial compressive state is as follows:

In the calculation,the strain state of each element is judged by the maximum tensile strain criterion first,and then by the Mohr-Coulomb criterion.If one criterion is met,tensile or compressive(shear)damage will occur.Otherwise the element is intact.During an earthquake,the element stress of a concrete slab is in the multi-axial stress state.When the stress meets the Mohr-Coulomb criterion,the maximum principal compressive strain εcmaxis used to replace the uniaxial compressive strain for damage judgments,which can be expressed as

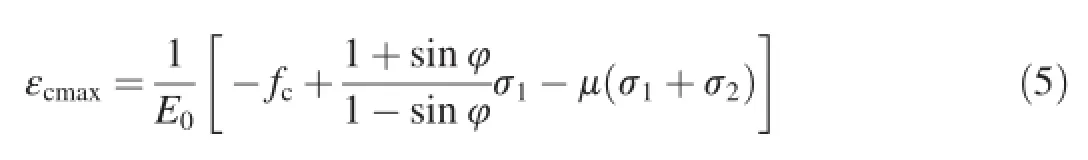
where fcis the compressive strength,μ is Poisson's ratio,φ is the friction angle,and σ1and σ2are the first and second principal stresses,respectively.

Existing research results indicate that the damage constitutive model for concrete,in which mesoscopic parameters are assigned to concrete elements according to certain rules,can simulate the failure process of concrete specimens under uniaxial tension,compression,and shear stress well(Zhong et al.,2009;Xiong et al.,2013).The macrocrack occurrence and expanding in the specimens are fairly displayed,and the failure pattern obtained with the model is in agreement with that of the experimental results.Different mesoscopic material structures show random failure patterns,but the failure mechanism remains the same.Moreover,this model can simulate the softening process of the stress-strain relationship under different conditions,which ref l ects the basic mechanical characteristics of concrete materials.

3.Random damage model for concrete slab considering mesoscopic inhomogeneity

Strictly speaking,in the concrete mesoscopic damagemodel, it is necessary to conduct element discretization for all of the aggregate,cement colloid,and interfaces,so as to take into account different mechanical behaviors of different parts and precisely simulate the damage process of concrete.Due to the limitation of computational capacity and complexity of the problem,it is impossible to implement this idea in large-scale concrete structures under the current conditions.Although a concrete slab is rather small,compared with the dam body in CFRDs,the volume of the concrete slab in a high CFRD is still relatively large.It is not realistic to conduct numerical calculation of concrete slabs in a strict mesoscale.Therefore,an imaginary concept of a so-called relative mesoscale is put forward in this paper,in which the inf l uence of mesoscopic inhomogeneity undertheassumptionofmacroscopichomogeneityofmaterialis considered,and the mesh of a concrete slab can be f i nely subdivided in the so-called relative mesoscale.

After a f i ne secondary subdivision of the concrete slab mesh,each slab element can be considered a continuous medium,but the mechanical properties,such as Young's modulus, the strength,and Poisson's ratio,are different for each element, which suggests discreteness and inhomogeneity.If the f i nely subdivided concrete slab mesh is regarded as a sample space, each slab element can be considered a sample.When the sample space is large enough,mechanical properties of the concrete slab can be considered random variables,which follow certain random distributions.The mean value of samples stands for the general level of the material's properties, and the variance represents the discrete degree.Although the mesoscopic structure of each concrete slab element cannot be described accurately with this method,as the mechanical properties of the slab are inhomogeneously distributed,with different orders of damage for different elements in the calculation process,the complex nonlinearmechanical behavior of the concrete slab can be simulated as a whole.

Weibull(1939)put forward the idea of adopting the method of probability to describe heterogeneous materials.It is impossible to measure the material failure strength accurately, but the probability of material failure when damage occurs at a given stress level can be well def i ned.Tang and Zhu(2003) and Chen(2001)held the view that the Weibull distribution, compared with the normal distribution,was more suitable for simulating the strain softening of inhomogeneous brittle materials.Thus,the Weibull distribution was used to characterize mesoscopic inhomogeneity of material parameters of concrete in this study.The elastic modulus and strength parameters were considered random variables,and assumed to follow the Weibull distribution.In the calculation process,material parameters following the Weibull distribution were assigned to each slab element randomly,and,thus,the concrete slab mesh was considered inhomogeneous.The density function of the Weibull distribution is

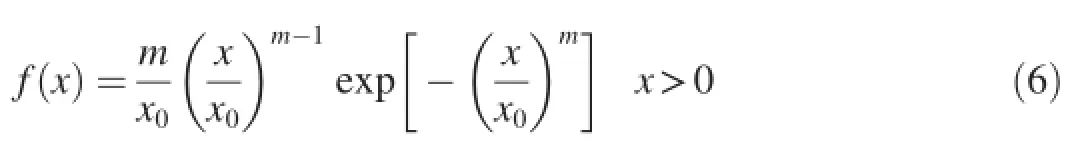
where x is a material parameter that follows the Weibull distribution,x0is a parameter related to the mean value of the material parameter x,and m is the shape parameter of the density function curve of the Weibull distribution.

The shape parameter m ref l ects the discrete degree of material parameters.With the increase of m,the density function curve changes from a low and wide shape to a high and narrow one,indicating that the material parameter x is closer to x0. Hence,m can also be called a homogeneity coeff i cient in this study.The larger the value m is,the more homogeneous the material is,and the lower the variance of the density function is.In specif i c calculation,random numbers of the uniform distribution are assigned values from 0 to 1,and then,according to the inverse function method and the density function of the Weibull distribution,those random numbers are utilized to form the material parameters.

4.Dynamic damage and cracking analysis of concrete slab for a high CFRD

4.1.Finite element model and calculation condition

A typical 100-m high CFRD was used in a case study.Both upstream and downstream slope ratios were 1:1.4.The finite element model of the dam with a f i nely subdivided mesh of the concrete slab is shown in Fig.2(a).Fig.2(b)shows the mesh of the maximum cross-section of the dam with f i ne slab elements.Figs.2(c)and(d)illustrate the details of original and fi nely subdivided slab elements,as well as cushion elements behind the slab in the transverse direction(zone A)and dam axial direction(zone B),respectively.Each nodal displacement at the dam bottom was f i xed in three directions.

For concreteslab elements,theelasticmodulusE, compressive strength fc,density ρ,and Poisson's ratio μ are given in Table 1.E and fcare random variables.Some parameters of concrete material are as follows:ξ=8,λ=0.1, r=0.3,and ζ=10.The mesoscopic parameters were obtained from the relationship curve between the mesoscopic and macroscopic elastic moduli and strength ratios according to the simulated results of Xiong et al.(2013).The Duncan E-B model and equivalent linear viscoelastic model were employed for the static and dynamic calculation of rockfill material,andcorresponding material parameters were obtained from Zhang (2015).The peripheral joint was simulated with a thin-layer element.The interface behavior between the slab and cushion was simulated with a nonlinear interface model using the thin-layer element,which was developed in commercial FEM software ADINA by Zhang et al.(2015b).

Table 1Macroscopic and mesoscopic parameters of concrete slab.

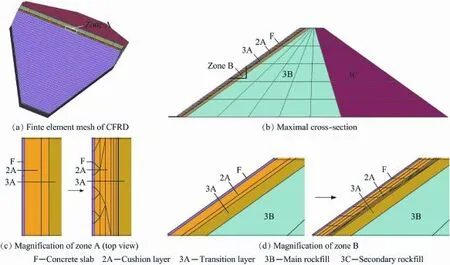
Fig.2.Finite element model of a CFRD.

The time histories of three acceleration components were introduced for dynamic analysis after static analysis.The total seismic duration was 20 s,and the time histories of acceleration of a 7.0-magnitude earthquake are shown in Fig.3,with peak values of 100,66.7,and 100 cm/s2in three directions. The time histories of acceleration of 8.0-and 9.0-magnitude earthquakes were obtained through proportional magnif i cation of that of the 7.0-magnitude earthquake.

4.2.Dynamic damage and cracking analysis of concrete slab

Fig.4 shows the distributions of dynamic damaged zones and macrocracks on the concrete slab during earthquakes with different seismic intensities.The distribution of dynamic damaged zones on the slab is mainly concentrated in the dam blocks on the riverbank within a range of 2/5 to 4/5 of the slab height.During a 7.0-magnitude earthquake,the damage to the slab shows local mesocracks or crack sprouting,without formation ofcontinuous macrocracking zones.With the increasing seismic intensity,more and more slab elements suffer damage,and the damaged zone gradually expands, mainly in the dam block on the riverbank.Some of the dynamic damaged elements then reach the damage threshold and macrocracks appear on the slab.Under low seismic intensity,there are few macrocracks on the concrete slab,and only a few completely destroyed elements connect,mainly in the range near the peripheral joint.With the increasing seismic intensity, more and more slab elements are completely destroyed and the zone on the slabs with destroyed elements,namely the macrocracking zone,grows wider.

Fig.3.Time histories of acceleration of 7.0-magnitude earthquake.

Fig.4.Distribution of dynamic damaged zone and macrocracking zone on concrete slab under earthquakes of different seismic intensities.

A magnified schematic diagram of local mesocracks on the slab from Fig.4(c)is demonstrated in Fig.5.The string of small red circles at a Gauss point of each element means that when the principal stress of concrete in a certain direction reaches the tensile strength,mesocracks will occur in the plane normal to the principal stress where the red circles exist.On the whole,the direction of mesocracks on the slab is roughly parallel to the peripheral joint.

Fig.5.Propagation direction of mesocracks on concrete slab in dam block on riverbank.

During a strong earthquake,the slab suffers the interactive effect of multidirectional tensile and compressive stresses. Thus,stress conditions are relatively complex.Once damage to an individual slab element occurs,mesocracks will occur on the slab,dynamically opening or closing during the earthquake.As damage to the elements becomes severe,the stress surrounding elements will be redistributed in a more concentrated pattern,causing mesocracks to expand continuously and generating macrocracks eventually.Calculation indicates that the tensile damage to the slab element is the main reason for the slab's cracking and complete destruction under strong seismic excitation.Figs.6 and 7 illustrate the distributions of damaged elements and macrocracking zones on the concrete slab at different times during a 9.0-magnitude earthquake,respectively(Here only the left half of the slab is displayed).The f i gures reveal that,with the increasing seismic duration,the damaged elements on the slab grow gradually,and the number of mesocracks on the slab increases signif i cantly,f i nally leading to a large damaged zone.With continuous deepening ofdamage,some elements are completely destroyed,mesocracks pass through adjacent elements,and then the macrocracking or crushed zone on the slab appears.Therefore,throughout the process of the earthquake, we can see the sprouting,developing,and expanding of the slab cracks,namely the dynamic formation and development of damage and cracking.

The percentages of damaged elements and macrocracking (completely destroyed)elements in the total slab element at different times during a 9.0-magnitude earthquake are shown in Fig.8.With the increasing seismic duration,the proportions of dynamically damaged and macrocracking elements do not increase linearly.Both increase signif i cantly in the first half of the earthquake,and later arrive at relatively stable values.At the end of the earthquake,the damaged and macrocracking slab elements account for around 26%and 5%of the total elements,respectively.

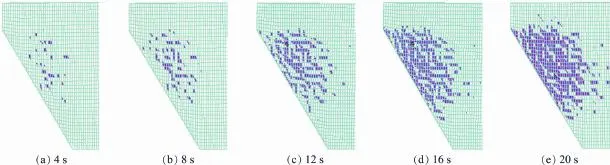
Fig.6.Distribution of damaged elements on concrete slab at different times during 9.0-magnitude earthquake.

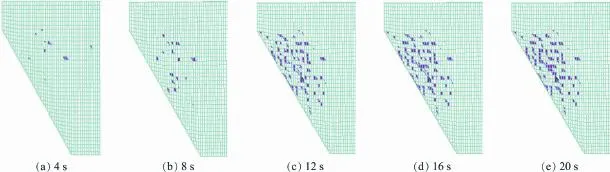
Fig.7.Distribution of macrocracking zone on concrete slab at different times during 9.0-magnitude earthquake.

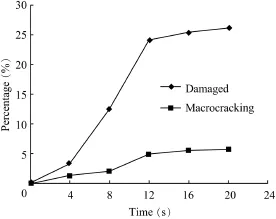
Fig.8.Percentages of damaged elements and macrocracking elements on concrete slab at different times under 9.0-magnitude earthquake.

There are many factors affecting the seismic response of a concrete slab under earthquake excitation.The dam prof i le has a large inf l uence on the dynamic cracking of the slab.Sensitivity analysis shows that,with the increase of the riverbank slope,the seismic effect on the dam gets stronger,the damaged zone on the slab gets wider,and corresponding macrocracks on the slab also increase.With the increasing seismic intensity, the inf l uence of the riverbank slope becomes more and more signif i cant.By contrast,the dam slope has little effect on the dynamic damage of the slab(Zhang,2015).The detailed calculation results will be illustrated in later research.

5.Conclusions

The concrete random mesoscopic damage model was extended to describe the dynamic damage behavior of concrete slabs in CFRDs.Compared with the conventional nonlinear viscoelastic or elastoplastic constitutive model,it can better describe the sprouting,growing,connecting,and expanding of slab cracks.Application of the model to a typical 100-m high CFRD shows that this model can well ref l ect the seismic response of a concrete slab during earthquakes.When the seismic intensity is low,the stress level of the slab is low, without damage or with slight damage to the slab;when the seismic intensity increases,the numbers of damaged and macrocracking elements on the slab ascend signif i cantly.After a 9.0-magnitude earthquake,the damaged and macrocracking elements account for about 26%and 5%of the total slab elements,respectively.The anti-seismic safety of the concrete slab is in a controllable state.

Arici,Y.,2011.Investigation of the cracking of CFRD face plates.Comput. Geotech.38(7),905—916.http://dx.doi.org/10.1016/j.compgeo.2011.06.004.

Bazant,Z.P.,Tabbara,M.R.,1990.Random particle models for fracture of aggregate or f i ber composites.J.Eng.Mech.116(8),1686—1705.http:// dx.doi.org/10.1061/(ASCE)0733-9399(1990)116:8(1686).

Chen,S.S.,Fang,X.S.,Qian,Y.J.,2011.Thoughts on safety assessment and earthquake-resistance for high earth-rock dams.Hydro Sci.Eng.(1), 17—21(in Chinese).

Chen,S.S.,Li,G.Y.,Fu,Z.Z.,2013.Safety criteria and limit resistance capacity of high earth-rock dams subjected to earthquakes.Chin.J.Geotech. Eng.35(1),59—65(in Chinese).

Chen,Y.Q.,2001.Numerical Simulations of Effective Mechanical Properties and Failure Process of Heterogeneous Materials.Tsinghua University, Beijing(in Chinese).

Huang,Z.Q.,Shen,X.P.,Tang,C.A.,2008.Numerical simulation of instability failure of high rolled compacted concrete gravity dam.J.Shenyang Univ. Technol.30(5),591—594(in Chinese).

Kong,X.,Zhou,Y.,Zou,D.,Xu,B.,Yu,L.,2011.Numerical analysis of dislocations of the face slabs of the Zipingpu concrete faced rockfill dam during the Wenchuan earthquake.Earthq.Eng.Eng.Vib.10(4),581—589. http://dx.doi.org/10.1007/s11803-011-0091-z.

Mazars,J.,1984.Application de la Mecanique de Lendnnag Emment an Comportememt non Lineaire de Structure.Ph.D.Dissertation.These de Doctorat Detat University,Paris(in French).

Mohamed,A.R.,Hansen,W.,1999.Micromechanical modeling of concrete response under static loading,Part I:Model development and validation. ACI Mater.J.96(2),196—203.

Schlangen,E.,Garboczi,E.J.,1997.Fracture simulations of concrete using lattice models:Computational aspects.Eng.Fract.Mech.57(2/3), 319—332.http://dx.doi.org/10.1016/S0013-7944(97)00010-6.

Tang,C.A.,Zhu,W.C.,2003.Damage and Fracture of Concrete.Science Press,Beijing,pp.120—145(in Chinese).

Wang,Z.J.,Liu,S.H.,Vallejo,L.,Wang,L.J.,2014.Numerical analysis of the causes of face slab cracks in Gongboxia Rockfill Dam.Eng.Geol.181, 224—232.http://dx.doi.org/10.1016/j.enggeo.2014.07.019.

Weibull,W.,1939.A Statistical Theory of the Strength of Materials.Generalstabens Litograf i ska Anstalts F¨orlag,Stockholm.

Wieland,M.,2009.The effects of the May 12,2008 Wenchuan Earthquake on large storage dams.Wasserwirtschaft 99(9),10—15.

Xiong,K.,Weng,Y.H.,He,Y.L.,2013.Seismic failure modes and seismic safety of hardfill dam.Water Sci.Eng.6(2),199—214.http://dx.doi.org/ 10.3882/j.issn.1674-2370.2013.02.008.

Xiong,K.,Hua,J.J.,Li,R.,2014.Static and seismic failure modes and structural safety of Oyuk Dam considering material heterogeneity.J. Yangtze River Sci.Res.Inst.31(7),74—80,90(in Chinese).

Xu,B.,Zou,D.G.,Kong,X.J.,Hu,Z.Q.,Zhou,Y.,2015.Dynamic damage evaluation on the slabs of the concrete faced rockfill dam with the plasticdamage model.Comput.Geotech.65,258—265.http://dx.doi.org/10.1016/ j.compgeo.2015.01.003.

Zhang,J.M.,Yang,Z.Y.,Gao,X.Z.,Zhang,J.H.,2015a.Geotechnical aspects and seismic damage of the 156-m-high Zipingpu concrete-faced rockfill dam following the Ms 8.0 Wenchuan earthquake.Soil Dyn.Earthq.Eng. 76(s1),145—156.http://dx.doi.org/10.1016/j.soildyn.2015.03.014.

Zhang,Z.Q.,2015.Study on Mechanism of Crack Damage of Concrete Slabs of High Concrete Face Rockfill Dams under Strong Earthquake.M.E. Dissertation.Hohai University,Nanjing(in Chinese).

Zhang,Z.Q.,Cen,W.J.,Yuan,L.N.,2015b.Application of interface element in dynamic analysis of CFRD.Appl.Mech.Mater.723,353—357.

Zhong,H.,Lin,G.,Li,H.J.,2009.Numerical simulation of damage in high arch dam due to earthquake.Front.Archit.Civ.Eng.China 3(3),316—322. http://dx.doi.org/10.1007/s11709-009-0039-9.

Received 23 August 2015;accepted 29 March 2016

This work was supported by the Key Laboratory of Failure Mechanism and Safety Control Techniques of Earth-rock Dams of the Ministry of Water Resources(Grant No.YK914019),the CRSRI Open Research Program(Grant No.CKWV2016376/KY),and the National Natural Science Foundation of China(Grant No.51009055).

*Corresponding author.

E-mail address:hhucwj@163.com(Wei-jun Cen).

Peer review under responsibility of Hohai University.

http://dx.doi.org/10.1016/j.wse.2016.09.001

1674-2370/©2016 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).

©2016 Hohai University.Production and hosting by Elsevier B.V.This is an open access article under the CC BY-NC-ND license(http:// creativecommons.org/licenses/by-nc-nd/4.0/).