超超临界燃煤机组直流锅炉水煤比软测量方法研究
张 维, 刘吉臻
(华北电力大学 新能源电力系统国家重点实验室,北京 102206)
超超临界燃煤机组直流锅炉水煤比软测量方法研究
张维,刘吉臻
(华北电力大学 新能源电力系统国家重点实验室,北京 102206)
摘要:以某1 000 MW 超超临界燃煤机组直流锅炉为例,提出了2种水煤比软测量方法:根据质量守恒定律和能量守恒定律建立基本计算模型,代入锅炉效率、煤种信息以及利用非线性最小二乘法拟合特性公式得出的工质焓升进行快速计算;利用综合自回归移动平均(ARIMA)模型时间序列法对滤波后水煤比数据进行参数估计和动态预测,并利用误差分析和验证该模型的准确性.采用这2种方法分别从机理分析和时间序列模型辨识角度对水煤比进行了快速计算和预测.结果表明:2种方法均能在一定程度上克服现阶段超超临界燃煤机组直流锅炉水煤比监测方法延迟大、误差大的缺点.
关键词:直流锅炉; 水煤比; 软测量方法; 焓升; 时间序列法
对于火电厂超超临界燃煤机组直流锅炉来说,迅速准确地测量出水煤比是保障锅炉安全、经济、稳定运行的前提.现有的水煤比传统监测方法(即采用给水量测量值与给煤量测量值的比值作为测量数据)存在迟延大、误差大的缺点.目前电厂给水量测量技术比较成熟,常规测量主要通过测量孔板进行,扣除小流量的测量误差外,给水量测量已经非常准确[1].给煤量测量广泛应用电子皮带秤,但是其受输送皮带的影响大、计量精度不高[2].国内电站锅炉基本还未实现入炉煤质和给煤量的实时准确测量[3].因此,对水煤比实时准确测量具有重要意义.
采用软测量技术是解决水煤比测量问题的有效途径之一.软测量技术通过建立易测变量与目标测量变量构成的数学关系,推断和估计目标测量变量数值,用软件来替代硬件,提高测量准确性和快速性.目前,软测量技术已经成为过程控制领域的研究热点之一,受到国内外学者和生产企业的广泛关注[4].以分散控制系统(DCS)为代表的先进控制系统在我国电力系统中得到广泛应用,利用其强大的数据采集、数据处理及传输功能,可配合软测量技术对水煤比进行实时监测,实现对相关过程的优化运行[5].
近年来,软测量技术被广泛应用于电力生产过程变量测量中.张恒等[1]根据汽水循环中的能量守恒定律和质量守恒定律算出水煤比的基准值,综合一种根据锅炉风量和排烟氧量计算热量的新型热量信号构造方法对水煤比进行修正,最终得出相对准确的水煤比.赵征等[6]采用燃烧机理分析和统计分析相结合的建模方法,首先建立起多个送风量和给煤量的软测量模型,然后对送风量和给煤量的多个软测量模型输出进行了加权数据融合,并将结果作为氧量软测量模型的输入;杨锡运等[7]对去趋势项的随机风速信号进行数据处理和比较,再用时间序列法对趋势项信号和处理后的信号分别进行预测和叠加,得到预测风速信号作为被测风速;梁秀满等[8]采用基于热平衡的机理建模方法,实现了球磨机出口温度的软测量,通过理论分析和离线仿真,证明该测量模型可以很好地描述实际对象的特性,说明了采用软测量技术对球磨机出口温度进行估计的可行性.
笔者在现有水煤比软测量方法的基础上,从机理分析角度,增加工质在汽水系统中焓值变化过程的推导,简化热量信号构造复杂度,细化超超临界直流锅炉运行过程变量测量位置;从时间序列模型辨识角度,利用基于综合自回归移动平均(Auto Regressive Integrated Moving Average, ARIMA)模型的时间序列法对滤波后水煤比运行数据进行参数估计和动态预测,此外若得到水煤比在变煤种、变负荷工况下实验数据,可拓展拟合该工况下水煤比计算模型.
1研究对象
研究对象为某1 000 MW超超临界燃煤机组,选用SG-3040/27.46-M型超临界塔式炉.在100%负荷下,工质从温度为294.8 ℃、压力为29.34 MPa、质量流量为2 733.4 t/h的锅炉给水吸收热量,转化为温度为605 ℃、压力为25.99 MPa、质量流量为2 733.4 t/h的过热蒸汽.
2基于工质焓升的水煤比计算模型
2.1利用守恒定律建立模型
根据质量守恒定律和能量守恒定律建立基本计算模型,即利用工质经从省煤器前至过热器后产生的焓升、质量流量与一次工质在锅炉内吸热量的关系,采集锅炉效率、煤种信息以及利用非线性最小二乘法拟合特性公式得出的受热部件前后工质焓升进行计算,得出适用于实际电厂的水煤比计算模型.
根据图1,锅炉给水由给水管道进入汽水系统,除喷水减温用水外,大部分给水依次通过图1中直流锅炉炉内各受热部件,在过热器出口处形成符合要求的一次工质(过热蒸汽).

图1 直流锅炉的工作原理示意图
一次工质有效吸热量为Q1,工质焓值由省煤器入口给水焓值hgs升高至高温过热器出口焓值hgr,工质变为过热蒸汽,即一次工质在整个过程中的焓值变化可利用稳定工况下的热平衡方程求出.
(1)
式中:qm,gs为给水质量流量,t/h.
同理,过热器出口的过热蒸汽在汽轮机高压缸做功后,排入锅炉再热器进行二次再热.假定一次工质的吸热量占锅炉内工质有效吸热量的份额为Ψ1,其余份额为二次工质吸热量所占份额,如果锅炉没有再热器,则Ψ1=1[9].因此,利用锅炉给水至过热器出口蒸汽的净吸热量占该净吸热量与再热器前后工质净吸热量之和的比值来表示Ψ1,由此可得
(2)
(3)
式中:m为燃料量,kg;Qnet,ar为燃料收到基低位发热量,kJ/kg;ηg1为锅炉热效率;qm,gr为过热蒸汽质量流量,t/h;qm,zr1为再热器入口蒸汽质量流量,t/h;qm,zr2为再热蒸汽质量流量,t/h;hzr1为再热器入口蒸汽焓值,kJ/kg;hzr2为再热蒸汽焓值,kJ/kg.
综合以上各式,可得到水煤比:
(4)
2.2模型算法中工质高精度焓值特性公式
模型求解重点工作为计算不同工况下水和水蒸气的焓值.目前焓值计算有多种方法,一般可采用水蒸气性质表内插求取,但这种方法不便于计算机应用;也可用国际公式化委员会(IFC)提出的水和水蒸气热力学性质计算公式在各编程软件中编程求取,但其计算形式极为复杂,需分区并使用双精度计算,迭代计算量大、浪费时间长,又占去工业计算机可观的内存.为提高工作效率、方便编程,已有学者使用稳定高效的非线性最小二乘法程序,根据1985年水和水蒸气骨架表,拟合了9个基本的水和水蒸气特性公式[10].根据这组高精度特性公式,对模型输入量划分合理筛选区间,选取有效测量值进行焓值计算.公式中符号和单位如下:温度为t,℃;绝对温度为T,K;压强为p,MPa;焓为h,kJ/kg;常量系数为a.
所选用的焓值拟合公式的具体形式见式(5)~式(8).
=a1+a2T+a3T2+

(5)
不饱和水:hgs=f2(p,t),p≤45 MPa,t≤350 ℃
hgs=(a00+a01v+…+a06v6)+(a10+a11v+…+
a16v6)u+(a20+a21v+…+a26v6)u2
(6)
u=3.6-p/9.806 65
(7)
v=t/100
(8)
由此将直流锅炉工质焓值拟合问题表述为一个无约束的非线性最小二乘问题,具体描述如下:
(9)
直流锅炉工质焓值拟合问题还可以表述为向量的乘积:
minQ=yTy
(10)
式中:y的元素为yi=[fi(x)-f0i]或者yi=[1-fi(x)/f0i];fi(x)为待拟合的函数;f0i为骨架表的中间值;x为待定的参数向量.
上述拟合公式的拟合范围如下:水蒸气,压力为0~35 MPa,温度上限为650 ℃;水,压力为0~45 MPa,温度上限为310~370 ℃,拟合范围覆盖了超超临界机组各种工况下热力特性计算的工质参数范围.
将拟合参数代入式(5)和式(6),求出不同工况下过热蒸汽、再热蒸汽和锅炉给水的焓值,并与相对应的过热蒸汽和不饱和水热力性质表中查得的焓值进行比较分析,该组焓值拟合公式所得焓值已经非常接近热力性质表中的焓值,所有公式偏差均在0.3%以内,能够满足高精度水煤比计算中对焓值计算的精度要求.此外,由于拟合公式形式简单,无需分区,不用双精度计算,迭代过程少而简单,因此计算速度比IAPWS297焓值计算速度快一个量级[10].
在得到工质焓值拟合公式后,将水煤比在线监测下的其他变量数据代入水煤比计算模型,因为该模型形式简单,工质焓值拟合公式编程方便,可利用各类编程软件进行编程或公式录入即可完成工况变化下的快速响应.
2.3实例分析
以某1 000 MW超超临界燃煤机组直流锅炉为例进行水煤比计算,选取2013-05-09 T 00:30—12:30、2013-05-26 T 00:00—24:00和2012-12-07 T 00:00—24:00 3种不同负荷下采样时段内水煤比计算模型中相关参数,并统计其平均值.
表1中数据为分别保持3种不同负荷稳态运行时相关参数的平均值,将其作为水煤比计算模型输入数据.其中,燃料收到基低位发热量采用电厂设计煤种的收到基低位发热量,锅炉效率采用通过测定并减去锅炉各项热损失后计算出的锅炉反平衡效率.此外,根据实际运行数据,统计锅炉给水、过热蒸汽和再热蒸汽对应的温度、压力和焓值数据合理区间,作为输入数据筛选区间,以保证参数合理性.
利用已建立的水煤比计算模型及Matlab程序,计算得出不同负荷下锅炉给水、过热蒸汽和再热蒸汽的焓值以及水煤比(见表2).由表2可知,计算结果可验证超超临界燃煤机组水煤比随负荷的升高而增大的结论.从能量平衡角度来看,高负荷下给水温度较高,若单位质量工质所需的吸热量较低,其需要的燃料量较少,则水煤比相对较大;同理,低负荷下水煤比相对较小[11].

表1 不同负荷下水煤比计算模型中的相关参数

表2 3种负荷下水煤比计算模型的计算结果
将2013-05-09 T 00:00—2:00机组在649.96 MW负荷下的稳态运行数据代入水煤比计算模型中,利用Matlab程序计算水煤比,并进行差值拟合,计算结果见图2.
由图2可知,基于工质焓升的水煤比计算方法能快速、准确地计算出水煤比,且在以工质参数为输入量的基础上,计入了煤种对稳态工况下水煤比的影响,可在一定程度上从数值计算的角度为超超临界燃煤机组提高主蒸汽参数和煤种设计等提供综合参考,同时也可作为直流锅炉整体数学建模分析工作的一部分.
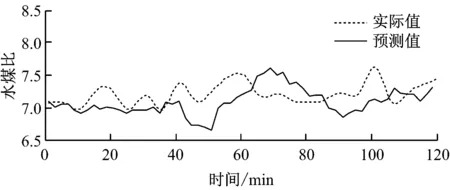
图2 水煤比计算模型的计算结果
从模型角度来看,工质焓值计算基于现有的高精度焓值拟合公式,在水煤比软测量过程中能够快速、准确地对工质焓值进行计算,计算过程迭代少、形式简单,有利于水煤比的快速测量和显示.今后可通过其他热量信号修正、细化锅炉内部部件焓升计算和减小采样区间等措施对该水煤比计算结果准确性进行进一步完善与提高.
3时间序列法及水煤比预测分析
时间序列法重点对相邻观测值本质特征依赖性进行阐述和分析,根据研究技巧对观测时间序列数据进行模型建立和动态描述,可用于对输出进行预测和控制,在随机最优控制和自适应控制中已得到广泛应用.
水煤比数据作为时间序列分析对象时,其不仅与以前时刻数据有关,还与以前时刻系统扰动存在依存关系,又因为水煤比数据呈现趋势性和周期性,因此需用ARIMA模型建模.
3.1建立基于时间序列的水煤比计算模型
若Xt为平稳、正态且零均值的时间序列,则其自回归移动平均模型即ARMA(p,q)模型为
(11)
式中:p和q分别为模型的自回归阶数和移动平均阶数;θ和φ均为不为零的待定系数;et为独立的误差项.
ARIMA模型定义中记B为滞后算子,Bk为k步滞后算子,即BkXt=Xt-k,对于d阶非平稳序列Xt而言,▽dXt是一个平稳序列,设其适合ARMA(p,q)模型:
(12)
(13)
(14)
称模型(12)为ARIMA模型,简记为ARIMA(p,d,q),其中d为模型的差分阶数.
ARIMA模型对水煤比预测的基本步骤如下:(1)根据水煤比原始时间序列的趋势图、自相关系数和偏自相关系数进行分析和平稳性识别;(2)平稳化处理,若时间序列为非平稳序列,则对序列进行差分处理,差分阶数递增直到序列自相关系数和偏自相关系数不显著地异于零;(3)模型辨识,根据序列自相关系数和偏自相关系数的截尾性和拖尾性对ARIMA模型进行类别辨识;(4)参数估计,对模型中的参数进行估计、检验;(5)假设检验,利用判定准则确定模型结果,诊断残差序列是否为随机误差;(6)利用检验模型结果对水煤比进行预测分析[12].
3.2求解基于时间序列的水煤比计算模型
3.2.1时间序列的模型识别
ARIMA模型自相关函数描述了观测值与之前时刻数据之间的相关程度;而偏自相关函数为在给定中间观测值的条件下观测值与之前时刻的相关程度[13].通过研究自相关函数和偏自相关函数可以识别ARIMA模型.遵循等时间间隔采样原理,采集机组在650 MW负荷下2013-05-19 T 11:00—11:20内、采样时间间隔为10 s的120个数据点.利用数据图、自相关函数和偏自相关函数相结合的检验方式对水煤比时间序列的平稳性进行检验,结果见图3~图5.

图3 原始数据趋势图
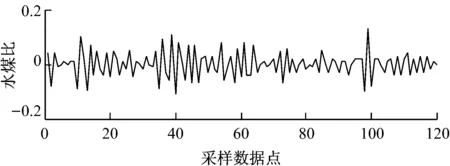
图4 一阶增量趋势图

图5 二阶增量趋势图
由图3可判定,原始时间序列为非平稳序列.由图4和图5可知,预处理后序列在0轴两侧摆动,趋势项被明显消减,得到较为平稳的时间序列,初步符合建模要求.但仅凭数据图识别结果是粗略的,需借助自相关函数和偏自相关函数进一步识别[14].因此,利用Matlab程序计算原始数据、一阶差分和二阶差分的自相关系数和偏自相关系数,结果见图6~图8.
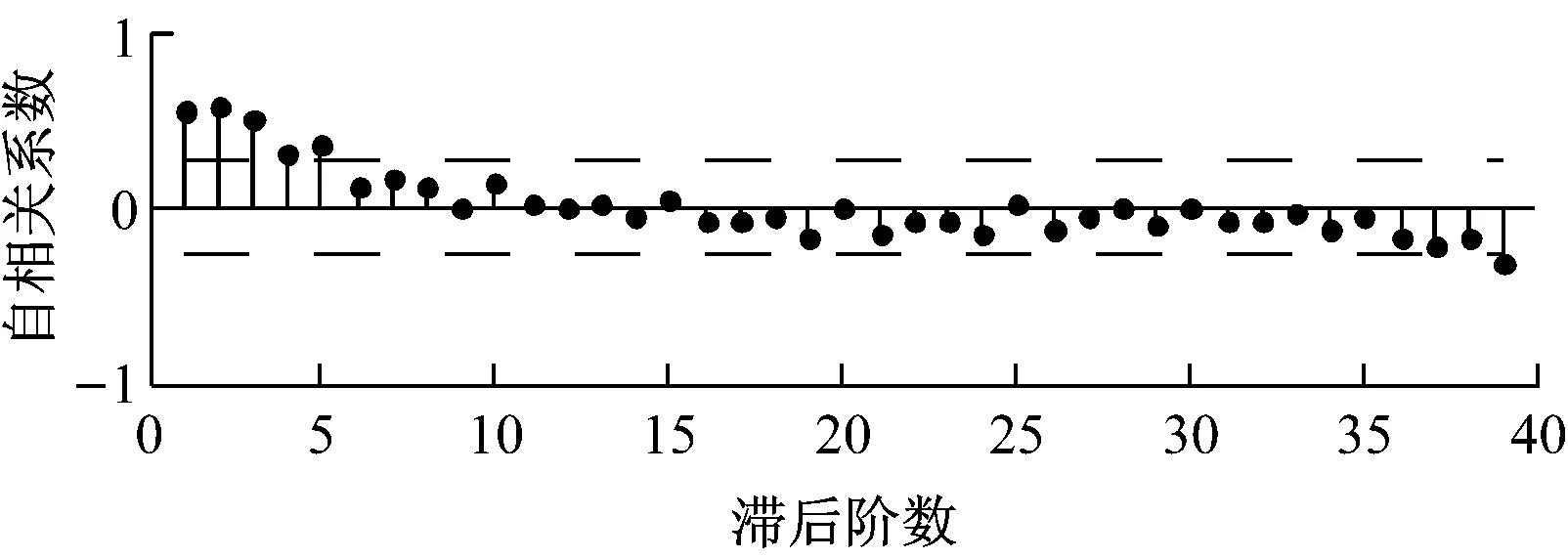
(a)
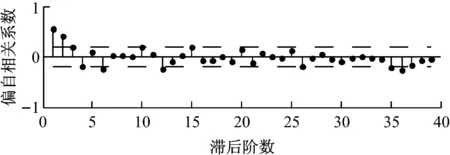
(b)
Fig.6Image analysis on autocorrelation coefficient and partial autocorrelation coefficient of the original data

(a)

(b)
Fig.7Image analysis on autocorrelation coefficient and partial autocorrelation coefficient of the first-order difference
由图6~图8可以看出,非平稳的水煤比数据序列差分后自相关系数快速衰减.根据时间序列法,序列达到平稳时的阶数即为差分阶数d,一阶差分序列的收敛效果更好,水煤比数据震荡性更小,所以选用的差分阶数为1.
此外,观察得出混合过程的自相关函数和偏自相关函数均是拖尾的,应选用ARIMA模型,即水煤比时间序列模型为d=1的ARIMA(p,1,q)模型.
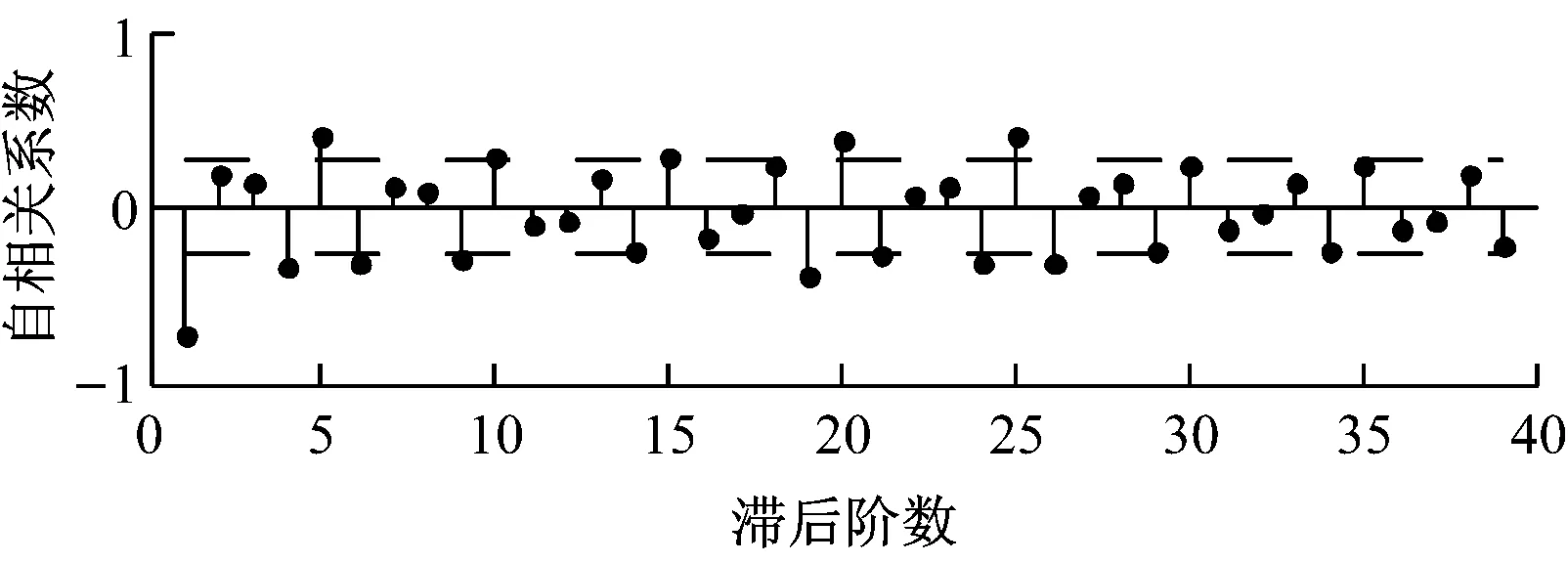
(a)
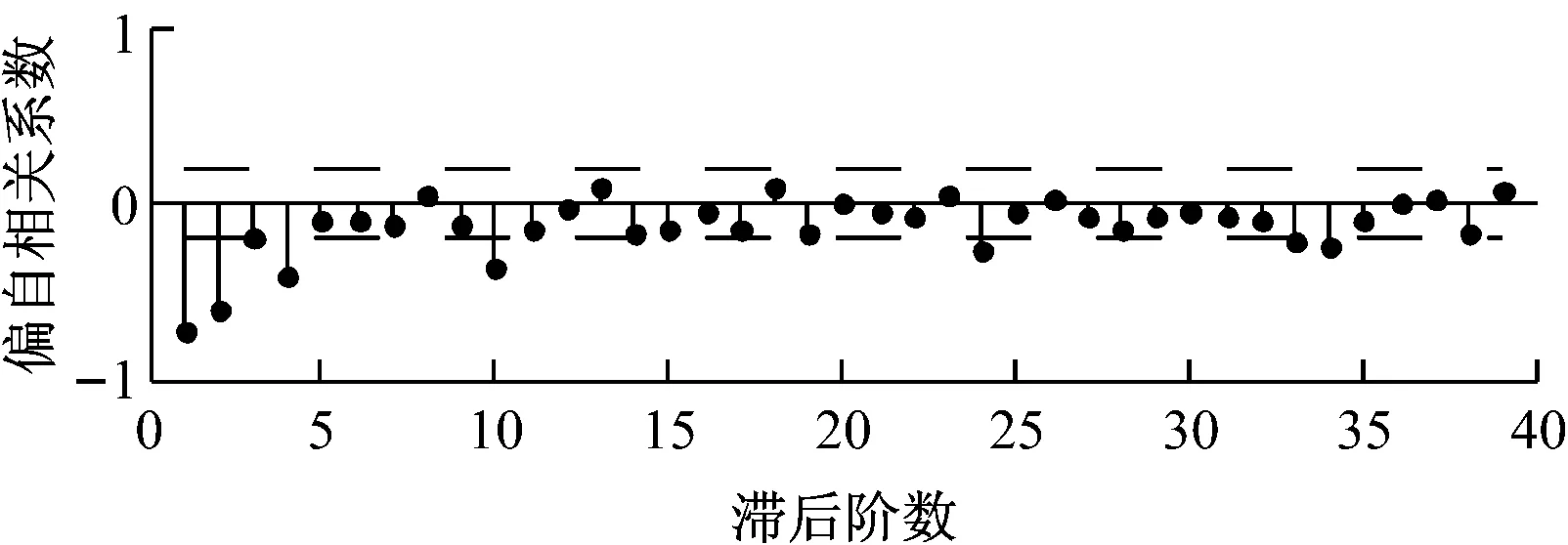
(b)
Fig.8Image analysis on autocorrelation coefficient and partial autocorrelation coefficient of the second-order difference
3.2.2定阶和适应性检验
根据时间序列法,模型的阶数需要通过水煤比一阶差分自相关系数和偏自相关系数确定.
偏自相关系数βk=0时,自回归(Auto Regressive, AR)模型的阶数为k-1;自相关系数ρk=0时,移动平均(Moving Average, MA)模型的阶数为k-1.分析图7数据,对于一阶差分序列,偏自相关系数βk在k=12时明显减小且接近零,而β12、β13又远小于β11,所以自回归阶数为11或12以内;同理,对于一阶差分序列,自相关系数ρk在k=8时接近零,而且ρ7、ρ8明显小于前面的数据,所以移动平均阶数为7或8以内.下面用最终预报误差(FPE)准则选择和验证模型阶数不大于ARIMA(12,1,8)的水煤比时间序列的最佳参数.
采用FPE最佳准则函数作为验证方法来进一步选择和验证.在初步确定的(12,8)以内,寻找最佳定阶方案.经Matlab程序计算作图,选择出最终预报误差最小、最适合采样时段内的水煤比时间序列的阶数,图9为FPE准则函数定阶图.

图9 FPE准则函数定阶图
当最终预报误差最小时(即图9中最低点)对应的p作为FPE准则确定的模型阶数,经判断确定水煤比时间序列最佳模型参数为ARIMA(10,1,7).
3.2.3参数估计及分析
根据上述分析,水煤比计算模型采用ARIMA(10,1,7)模型来描述,模型参数估计采用历史数据作为数据源,从中选用120个数据作为水煤比样本数据,建立计算模型,利用Matlab程序训练数据样本,进行参数估计.获得水煤比计算模型后,检验模型的有效方法之一是利用实际的输入、输出数据计算模型未来的输出精度[14].利用函数predict进行模型的预测输出.对选定的120个数据样本零均值化、平稳化后进行训练,建立的ARIMA模型描述为
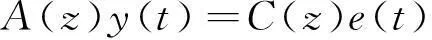
(15)
式中:A(z)和C(z)为式(13)和式(14)中z域表达式.
根据以上计算,可以确定水煤比的参数模型为
Xk+1=Xk-1.321Yk-1-1.036Yk-2+0.617 4Yk-3-0.375 8Yk-4-0.241 7Yk-5+0.066 29Yk-6-
0.160 5Yk-7-0.419 6Yk-8-0.560 3Yk-9-
0.347 2Yk-10+ek+0.793 2ek-1+0.690 7ek-2+
0.548ek-3+0.261ek-4-0.521 3ek-5
(16)
式中:Yk为水煤比数据样本Xk的一阶差分序列.
水煤比的时间序列模型已经建立,其适用性还需进一步验证,首先利用水煤比原始数据信号对预测值进行检验,经Matalab程序计算作图,对比效果如图10所示.
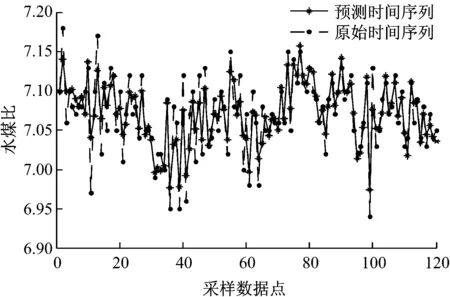
图10 原始时间序列和预测时间序列对比图
由图10可以看出,模型的水煤比预测值与样本值的变化趋势基本吻合,在采样时段内预测点与样本点接近,整体来说模型的参数预测比较准确,由此可以推断所建立的水煤比计算模型可用来估计未来短时期或较长时期的水煤比变化趋势及定量值,为电厂水煤比控制提供参考.
从误差的角度考察模型,预测值与样本值之间的误差较小(见图11).
此外,水煤比时间序列模型建模时还需要考虑模型预测误差的相关性,确定模型误差为随机误差,此处用误差序列的自相关函数进行描述,可以了解时间序列的平稳性和时间趋势特征[15].利用Matlab程序进行水煤比计算模型预测误差序列的自相关函数分析,结果如图12所示.
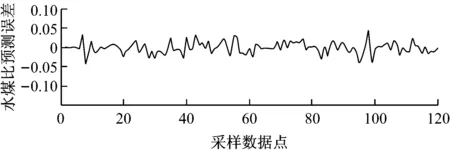
图11 原始时间序列和预测时间序列误差

图12 预测误差序列的自相关函数
由图12可知,误差序列自相关函数为0附近的一系列数值即可说明误差序列归一化后序列当前值与其滞后值关联程度低,误差为随机误差,序列不存在误差记忆性,可推断基于ARIMA时间序列的水煤比计算模型用于预测水煤比时的适用性较好[14].此外,时间序列法适应性强,如果能够得到采样时段内变负荷、变煤种工况下的水煤比数据,就能对各工况下水煤比进行建模和预测.
42种方法的对比
基于锅炉受热部件焓升的水煤比计算模型利用已有的水煤比计算思路,结合实际电厂运行数据,根据质量守恒定律和能量守恒定律,通过电厂常见且易测量的温度、压力和流量等测量信息,建立基于锅炉受热部件焓升的水煤比计算模型,再利用计算机系统对经锅炉受热部件后的工质进行焓升计算,得出适用于实际电厂的水煤比在线计算结果.该模型不需要超临界直流锅炉内复杂的受热面信息,仅已知省煤器前给水信息、过热器后过热蒸汽信息、再热器前后再热蒸汽信息以及锅炉效率和设计煤种收到基低位发热量即可进行计算,该模型和计算方法具有便于应用的特点,计算结果较准确、快速,可适用于电厂实际应用和水煤比的简便计算.
以ARIMA模型为基础的时间序列法水煤比计算方法经过数据采样,数据预处理,模型分类、识别及定阶,模型适应性检验的全过程,建立起水煤比数学模型.以火电厂实际机组运行中的水煤比为研究对象,利用时间序列法对水煤比进行参数估计和动态预测,根据电厂实际运行数据建立了水煤比的ARIMA(10,1,7)模型,经过校验分析和预测误差分析、验证,表明该模型适用性好、准确性高,可对稳态工况下水煤比进行预测,也可以进行模型拓展来拟合不同煤种、负荷等工况下的水煤比[14].
若在仅已知工质状态、锅炉参数的稳态工况下,可利用基于锅炉受热部件焓升的水煤比计算模型进行水煤比快速计算,模型中的焓值拟合公式能够达到电厂热力计算精度且计算快速、简便,该方法依赖工质温度、压力和流量等现场参数的准确测量,存在一定的滞后性,但相比其他计算方法较为快速、简便.若在已知过去一段时期水煤比准确数据的前提下,可采用以ARIMA模型为基础的水煤比计算模型进行预测,该模型能够较为准确地预测不同工况下的水煤比及其变化趋势,得到水煤比时间序列递推公式,能够预测未来一定时段内的水煤比.
5结论
研究了2种水煤比软测量方法,分别从机理分析和时间序列法模型辨识角度对水煤比进行快速计算,2种方法可适用于不同工况下的电厂水煤比计算与预测,在一定程度上克服了现阶段超超临界燃煤机组直流锅炉水煤比监测方法延迟大、误差大的缺点.研究结果有利于对超超临界直流锅炉进行预控制,对其主蒸汽温度和锅炉给水控制具有一定的参考价值.
参考文献:
[1]张恒, 刘吉臻, 钟亮民, 等. 一种超超临界直流锅炉水煤比软测量方法[J]. 电站系统工程, 2014,30(5):19-22.
ZHANG Heng, LIU Jizhen, ZHONG Liangmin,etal. A kind of soft measuring method of ultra-supercritical once-through boiler water-coal ratio[J]. Power System Engineering, 2014,30(5):19-22.
[2]郝明, 田民, 张文焱. 刮板给煤机煤量在线监测系统的设计与实现[J]. 自动化技术与应用, 2011,30(4): 85-87.
HAO Ming, TIAN Min, ZHANG Wenyan. The design and implementation of the online monitoring system for coal feed amount on embedded scraper[J]. Techniques of Automation & Applications, 2011,30(4): 85-87.
[3]冯有为. 基于软测量技术的电站锅炉煤质/煤量在线监测系统的研究[D]. 武汉:华中科技大学, 2011.
[4]傅永峰. 软测量建模方法研究及其工业应用[D]. 杭州: 浙江大学, 2007.
[5]韩璞, 乔弘, 王东风, 等. 火电厂热工参数软测量技术的发展和现状[J]. 仪器仪表学报, 2007, 28(6): 1139-1146.
HAN Pu, QIAO Hong, WANG Dongfeng,etal. Development and current status of thermal parameter soft-sensing technique in power plant[J]. Chinese Journal of Scientific Instrument, 2007, 28(6): 1139-1146.
[6]赵征, 曾德良, 田亮, 等. 基于数据融合的氧量软测量研究[J]. 中国电机工程学报, 2005, 25(7): 7-12.
ZHAO Zheng, ZENG Deliang, TIAN Liang,etal. Research on soft-sensing of oxygen content based on data fusion[J]. Proceedings of the CSEE, 2005, 25(7): 7-12.
[7]杨锡运, 孙翰墨. 基于时间序列模型的风电场风速预测研究[J]. 动力工程学报, 2011, 31(3): 203-208.
YANG Xiyun, SUN Hanmo. Wind speed prediction in wind farms based on time series model[J]. Journal of Chinese Society of Power Engineering, 2011, 31(3): 203-208.
[8]梁秀满, 孙文来. 钢球磨煤机出口温度软测量方法[J]. 机械与电子, 2000(6): 14-16.
LIANG Xiuman, SUN Wenlai. Soft measuring method for outlet temperature of steel ball mill[J]. Machinery & Electronics, 2000(6): 14-16.
[9]李遵基. 热工自动控制系统[M]. 北京:中国电力出版社, 1997.
[10]蒋寻寒, 曹祖庆. 一组性能优良的水和水蒸汽高精度特性公式[J]. 动力工程, 2003, 23(6): 2777-2780.
JIANG Xunhan, CAO Zuqing. A group of simple precise formulations for properties of water and steam[J]. Power Engineering, 2003, 23(6): 2777-2780.
[11]梁丽博. 基于关联规则的超临界锅炉水煤比控制研究与应用[D]. 保定:华北电力大学, 2009.
[12]仇建平, 陈立潮, 张英俊, 等. 基于社会网络的个人需求预测算法研究[J]. 计算机应用与软件, 2014, 31(2): 263-265.
QIU Jianping, CHEN Lichao, ZHANG Yingjun,etal. Study on social networks based individual demand prediction algorithm[J]. Computer Application and Software, 2014, 31(2): 263-265.
[13]王璐. 风电场的风速预测与主轴故障诊断[D]. 北京:华北电力大学, 2010.
[14]张文琴. 反向建模方法的一般规律及其应用[D]. 北京:华北电力大学, 2009.
[15]王国锋, 王子良, 王太勇, 等. Matlab在时间序列分析中的应用[J]. 应用科技, 2003, 30(5): 36-38.
WANG Guofeng, WANG Ziliang, WANG Taiyong,etal. Application of Matlab in time series analysis[J]. Applied Science and Technology, 2003, 30(5): 36-38.
A Soft Measurement Method for Water-Coal Ratio of an Ultra-supercritical Once-through Boiler
ZHANGWei,LIUJizhen
(State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources,North China Electric Power University, Beijing 102206, China)
Abstract:Taking a 1 000 MW ultra-supercritical once-through boiler as an example, two methods were proposed for soft measurement of water-coal ratio in the once-through boiler. One is to quickly calculate the water-coal ratio using basic calculation models built up based on the law of mass and energy conservation, by substitution with the boiler efficiency, coal grade and the enthalpy rise of water obtained by nonlinear least square method; the other is to dynamically estimate and predict the water-coal ratio after wave filtering with auto regressive integrated moving average (ARIMA) time series method, of which the accuracy is to be verified by error analysis. With above two methods, the water-coal ratio was respectively calculated and predicted through mechanism analysis and time series model identification. Results show that both the methods can to some extent overcome the shortcomings of traditional monitoring methods for once-through boiler of ultra-supercritical coal-fired units, such as large delay, big error, and so on.
Key words:once-through boiler; water-coal ratio; soft measurement method; enthalpy rise; time series analysis
文章编号:1674-7607(2016)02-0099-08
中图分类号:TK229.2
文献标志码:A学科分类号:470.30
作者简介:张维(1991-),女,满族,河北秦皇岛人,硕士研究生,主要从事直流炉机组建模与软测量技术方面的研究.电话(Tel.):18810278985;E-mail:ncepuzw@163.com.
基金项目:国家重点基础研究发展计划(973计划)资助项目(2012CB215203)
收稿日期:2015-04-07
修订日期:2015-06-01

