固结弹性薄层的空间轴对称接触问题

朱　凯，张　旭，马　清（遵义师范学院工学院，贵州遵义563002）



固结弹性薄层的空间轴对称接触问题

朱凯，张旭，马清
（遵义师范学院工学院，贵州遵义563002）

摘要：基于弹性理论研究了刚性基底上固结弹性薄层的空间轴对称接触问题，采用合理假设位移分段函数的方法，求解弹性薄层的应力分量，最终获得能满足所有边界条件应力的解析解，避免了复杂的数学理论，同时弥补了三维接触问题中运用Johnson假设进行求解所带来的缺陷。

关键词：弹性薄层；空间轴对称；应力分量；分段函数；Johnson假设

有关弹性薄层的空间轴对称接触问题已有众多学者研究。其中Johnson[1]研究了弹性薄层的二维接触问题，主要集中在薄层厚度远小于接触半径（b<< a）的特殊情况，并形成了著名的Johnson假设，即“薄层厚度远小于接触半径时，认为薄层上下变形均匀是合理的”，在弹性薄层固结刚性基底的情况下，此假设等同于“薄层没有水平位移”。此后很多学者关于薄层三维接触问题的研究均建立在此假设的基础上。Jaffer[2]以Johnson假设为基础，主要研究了当弹性薄层为可压缩材料并且与刚性基底固结时，接触压应力的分布情况，但未涉及位移场和应力场的分析。Barber[3]采用不同的方法研究了接触压应力的分布。Ning等[4]以Johnson假设为基础，利用Abaqus对接触区域压力进行有限元分析，所得结果与理论结果基本吻合，但所得应力分量完全无法满足边界条件，这也是利用Johnson假设求解空间接触问题的缺陷。Jaffer[5]的另一篇论文以Popov[6]和Alexandrov[7]的成果为基础，假定压力分布及位移函数为修正Legendre多项式的展开形式，涉及到复杂数学理论的应用。Mattthewson[8]在1980年提出了求解薄层空间轴对称问题的新方法，通过分析厚度方向平均应力、应变得到此问题的近似解，并着重分析了当泊松比v为0.5时，弹性薄层作为基底保护层的应力场、位移场。还有许多学者[9-12]对该问题进行了大量的研究。

通过对以往建立在Johnson假设上的文献的分析不难得知，利用该假设求解薄层接触问题最终将导致薄层上表面的切应力边界条件完全无法满足。本文旨在通过一种简单的数学方法得到弹性薄层应力的解析解，利用分段函数的形式，合理假定径向位移分量和竖向位移分量，最终得到能完全满足所有边界条件的应力分量，为固结薄层接触问题的求解提供理论依据。

1问题的建立

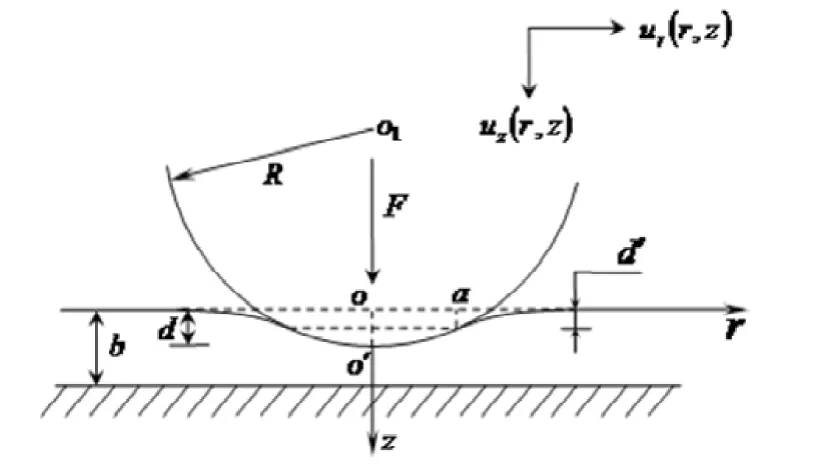
图1刚性基底上固结弹性薄层与刚性球状压头的法向接触

2边界条件

由图1可知，刚性圆球与薄层之间的接触区域为球冠状，接触半径为。刚性圆球与薄层之间的界面假定不受摩擦的影响，同时由图1可知，只有接触区域内有应力分布，故可得边界条件如下：

3问题的求解

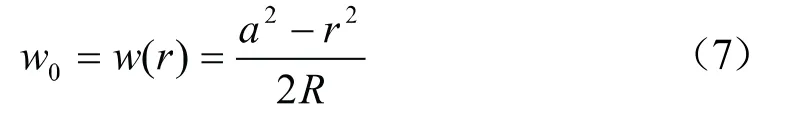
为了确保接触区域为无摩擦状态以及式（5）能得到满足，径向位移不能处处为0，否则将造成切应变处处不为0的情况，进而接触区域将存在切应力。故可假设径向位移有如下形式：

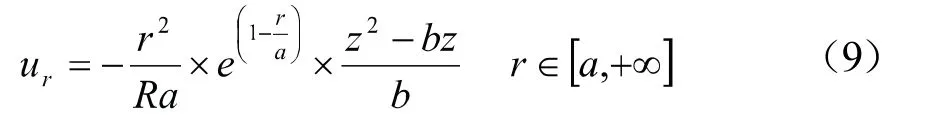
研究Ning等[4]的文献，不难发现其最大的缺陷在于薄层应力表达式完全无法满足薄层表面的切应力边界条件，故以此为切入点，为满足应力边界条件

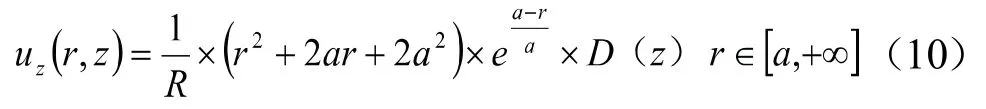
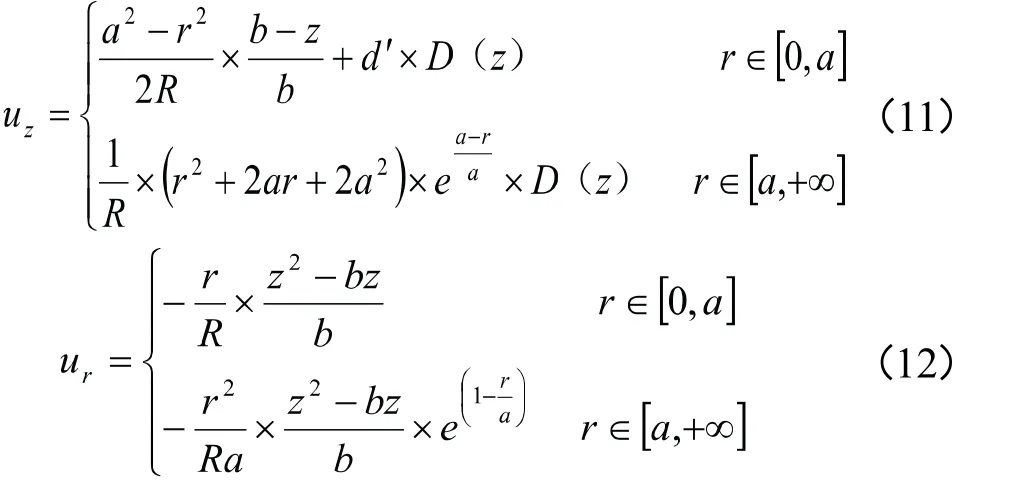
进而可求得弹性层的应力分量为：

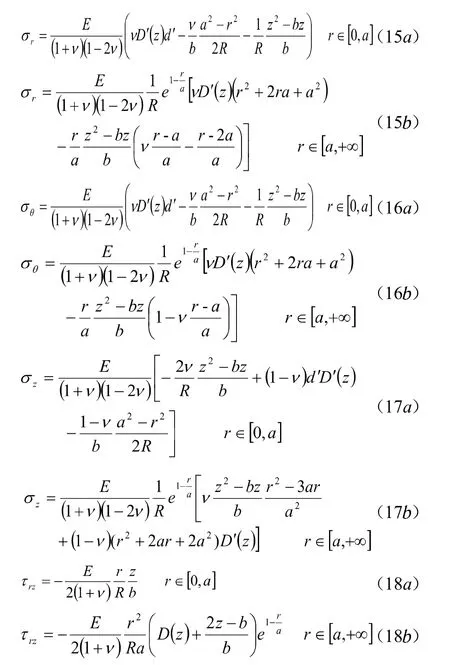
4讨论

本文中的模型与Ning等[4]的略有不同，但所得解析解仍适用于各向同性可压缩材料。由图1可知刚性球体周围的弹性薄层发生了凹陷，此种变形有点类似Hertz有关半空间受压头挤压时的变形情况，其成果在Popov[13]的著作中已提及。Popov[13]用图的形式描述了接触区域外弹性薄层的表面位移随径向的变化情况，将本文的结果与其进行对比，如图2所示。通过对比，不难发现，由Hertz理论得出的位移无量纲随径向无量纲的变化要显著些，而本文中得出的位移曲线要平缓些。这主要是由于在缺乏刚性基底的阻抗作用下，压头下方弹性薄层材料在受压后的变形主要由竖向移动获得，而在有刚性基底的情况下，弹性薄层材料的流动则集中在径向位移。压头周围径向位移越大，表明越多的材料被移出该区域，这样便造成该区域较大凹陷的形成。

图2弹性层表面（z=0）接触区域外的竖向位移变化

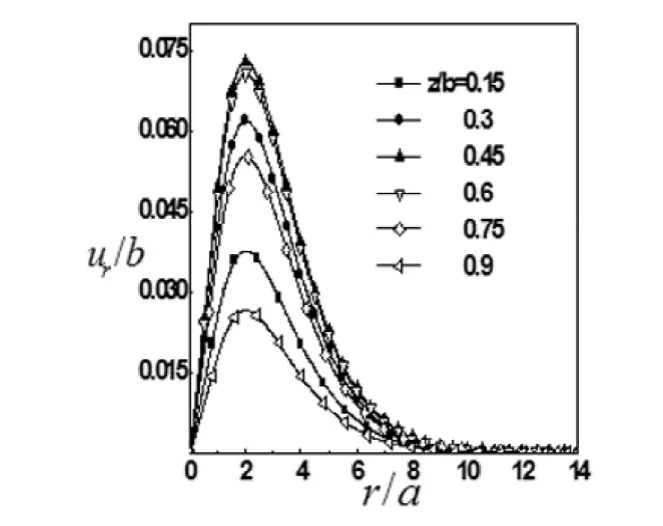
图3 a=2b，v=0.3时层中各处径向位移的变化

图3为径向位移的变化情况，从图3可看出，材料的径向流动主要集中在弹性薄层的中下部位约=2a的位置，表层和下交界面无径向位移变化。故当压头作用于弹性薄层后，弹性薄层材料往≈2a的位置聚集，压头周围弹性薄层中下部位材料的移出自然而然造成了上部材料的较大凹陷。

本文最大的创新点在于薄层无摩擦接触问题中所有边界条件得到了满足，这源于位移分段函数的运用。然而，位移函数采取分段的形式却带来了一缺陷，即切应力在=a处并不连续，出现了阶跃的现象。通过分析发现，这种现象主要是由于造成的，为了解决这个问题，分别拟定了的四种形式，并通过在图4中进行对比，反应了每一个对切应力不连续问题所造成的影响。其中表示=a处，截面左端的切应力，而则表示该截面右端的切应力受影响。分别取值1、2、3、4。通过观察可知，取时，可将切应力在=a处不连续的影响降到最低，误差基本可忽略不计，不影响应力分量作为近似解的有效性及精确性。故采用作后续讨论。同时，从图4中不难看出，无论取何种形式，切应力在弹性薄层与基底接触面处是恒连续的。

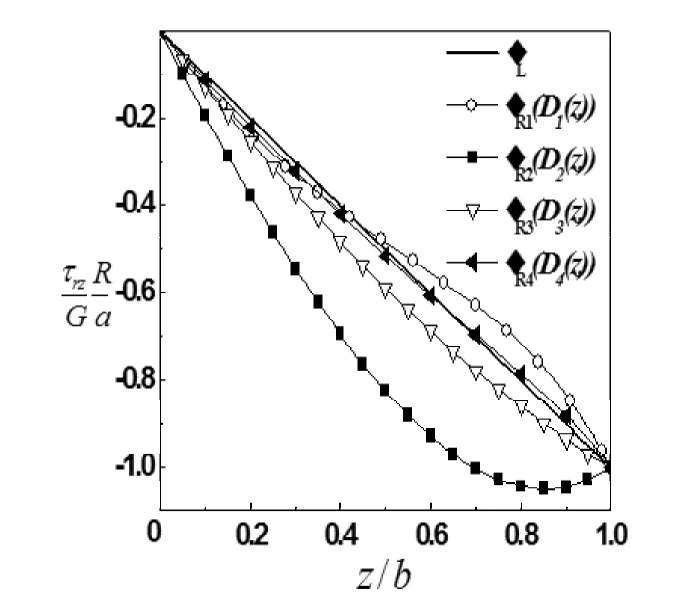
图4 a = 2b，v = 0.3时r = a处D(z)对切应力不连续的影响

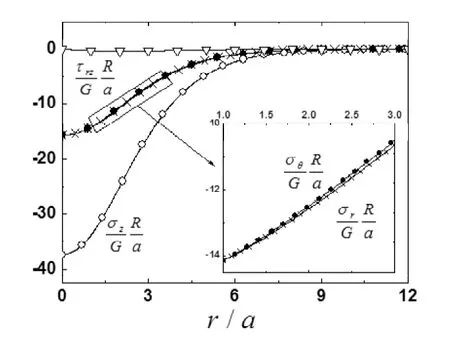
图5 v = 0.3，a= 2b时z = 0.25b处应力随径向的变化

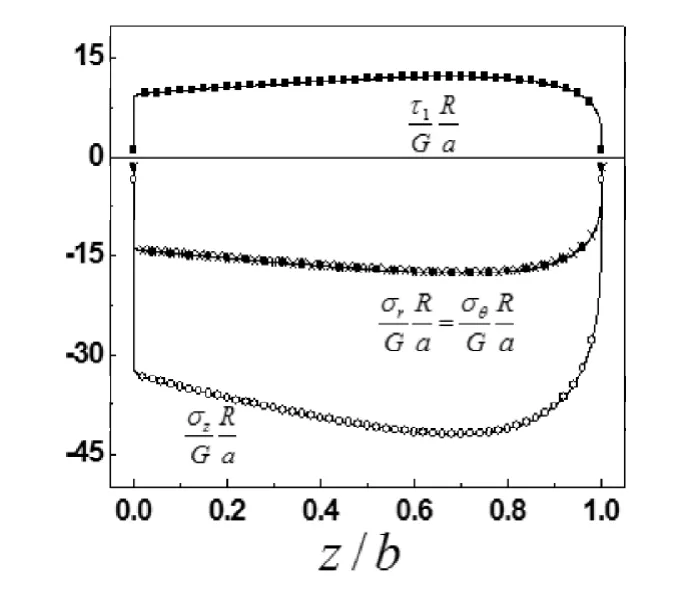
图6 v = 0.3，a = 2b时r = 0处应力随z轴的变化

图7 v = 0.3，a = 2b时zr平面内的Von Mises等效应力图

5结论

本文基于弹性理论，通过拟定位移分段函数的方法，研究了弹性薄层的空间轴对称接触问题，并获得薄层应力分量的解析解。所得结论如下：

（1）弹性薄层中最大压入深度、接触半径及刚性

（2）弹性薄层上交界面和下交界面的正应力基本一致。

参考文献：

[1]Johnson KL.Contact mechanics[M]. Cambridge:Cambridge university press,1987.

[2]Jaffar MJ.Asymptotic behaviour of thin elastic layers bonded and unbonded to a rigid foundation[J].International Journal of Mechanical Sciences,1989,31(3):229-235.

[3]Barber JR.Contact problems for the thin elastic layer[J].International Journal of Mechanical Sciences,1990,32(2):129-132.

[4]Ning X,Lovell M,Slaughter WS.Asymptotic solutions for axisymmetric contact of a thin transversely isotropic elastic layer[J].Wear,2006,260(7):693-698.

[5]Jaffar MJ.A numerical solution for axisymmetric contact problems involving rigid indenters on elastic layers[J].Journal of the Mechanics and Physics of Solids,1988,36(4):401-416.

[6]Popov GI.The contact problem of the theory of elasticity for the case of a circular area of contact[J].Journal of Applied Mathematics and Mechanics,1962,26(1):207-225.

[7]Aleksandrov VM.Asymptotic solution of the contact problem for a thin elastic layer[J].Journal of Applied Mathematics and Mechanics,1969,33(1):49-63.

[8]Aleksandrov VM.On the approximate solution of a certain type of integral equation[J].Journal of Applied Mathematics and Mechanics,1962,26(5):1410-1424.

[9]Meijers P.The contact problem of a rigid cylinder on an elastic layer[J].Applied Scientific Research,1968,18(1):353-383.

[10]Alblas JB,Kuipers M.On the two dimensional problem of a cylindrical stamp pressed into a thin elastic layer[J].Acta Mechanica,1970,9(3-4):292-311.

[11]Gladwell GML.On some unbonded contact problems in plane elasticity theory[J].Journal of Applied Mechanics,1976, (43):263.

[12]Matthewson MJ.Axi-symmetric contact on thin compliant coatings[J].Journal of the Mechanics and Physics of Solids, 1981,29(2):89-113.

[13]Popov VL.Contact mechanics and friction[J/OL].Springer Berlin Heidelberg,2010.

（责任编辑：朱彬）

Axisymmetric Contact Problem of the Bonded Elastic Thin Layer

ZHU Kai; ZHANG Xu; MA Qing
(College of Engineering and Technology, Zunyi Normal College, Zunyi 563002, China)

Abstract：The axisymmetric contact problem for the elastic thin layer bonded to rigid foundation is concerned on the basis of the theory ofelasticity.A method with the application of thedisplacementpiecewise function is presented to getthe stress components ofthe elastic thin layer, and analytical solution of the stress components is obtained finally. The method is simple and the defect of the application of Johnson’s assumption to space problems is remedied.

Key words：elastic thin layer; axisymmetric contact; stress components; piecewise function; Johnson’s assumption

作者简介：朱凯，男，湖南娄底人，遵义师范学院工学院助教，硕士。研究方向：接触力学与摩擦。

收稿日期：2015-09-12

中图分类号：O343.3

文献标识码：A

文章编号：1009-3583（2016）-0107-04