船舶纵向下水曲线直接计算法

林诗尧，孙江龙，2，3，曾荆州，解德，2，3

1华中科技大学船舶与海洋工程学院，湖北武汉430074 2船舶和海洋水动力湖北省重点实验室，湖北武汉430074 3高新船舶与深海开发装备协同创新中心，上海200240



船舶纵向下水曲线直接计算法

林诗尧1，孙江龙1，2，3，曾荆州1，解德1，2，3

1华中科技大学船舶与海洋工程学院，湖北武汉430074 2船舶和海洋水动力湖北省重点实验室，湖北武汉430074 3高新船舶与深海开发装备协同创新中心，上海200240

摘要：提出一种船舶纵向下水曲线的直接计算法。将船体外表面假设为刚性面，利用商用有限元软件ABAQUS/AQUA模块对纵向下水曲线进行直接计算。针对一艘方形驳船，将直接计算获得的6条下水曲线与传统邦戎曲线方法的结果进行比较，两者吻合很好；通过针对一艘型线变化较大驳船的计算，发现该方法对网格尺寸不敏感，验证了所提方法的准确性和便捷性。将该方法进一步应用于Wigley船型和油船，验证了其可行性和普适性。算例表明，所提出的直接计算法具有潜在的工程应用价值。

关键词：纵向下水；下水曲线；直接计算法；邦戎曲线法；ABAQUS/AQUA

0　引　言

随着设计工具的更新与建造工艺的进步，为了提高远洋运输的效率，船舶日益大型化。由著名的Knock Nevis号改建而成的超巨型油船（ULCC）Mont号，其载重量达564 763 t；2014年下水的中海“环球”号集装箱船的载货量达19 100 TEU；2010年下水的特大型矿砂船（VLOC）MS Vale Brasil号的载重量已达402 347 t。此类特大型船舶，以及大、中型船舶的下水过程一旦出现问题，后果将十分严重，轻则造成不可挽回的经济损失，重则可能导致工作人员的伤亡。因此，人们往往高度重视船舶下水过程的安全性。

一般来说，船舶下水分为重力式下水、浮力式下水以及机械式下水3大类。其中，重力式下水主要包括纵向滑道下水以及横向滑道下水2类，我国船舶主要采用纵向下水方式；浮力式下水包括干船坞下水与浮船坞下水；机械式下水主要由升船机或吊车进行吊放，一般应用于小型船舶。相对来说，船舶漂浮式下水较为安全，其下水期间可能出现的问题主要是倾角过大而导致的失稳［1］。机械式下水由于船舶尺度较小，可能出现的问题并不多。而重力式下水可能会出现因摩擦力过大导致不下滑、浮力不足导致艉落或者艏落，以及限制水域内滑程过长等问题。因此，目前国内、外的研究主要集中在重力式下水方面，尤以广泛采用的纵向下水为主。本文拟主要针对纵向重力式下水问题进行研究。

对船舶纵向下水问题的研究主要分为2类。第1类问题是将船舶下水认定为一个动力学过程，通常需借助CFD技术进行分析。吴晶［2］利用LS-DYNA流固耦合模块分析了动力学下水过程，并考虑了自由液面、接触等因素。王文华等［3］开发了基于CFD的船舶下水水动力分析法，与实测结果吻合较好，随后基于该分析法［4］又研究了船台及船体各状态参数对船舶下水运动的影响。在这类问题中，也有较多的学者采用经验或理论公式来计算下水中船舶受到的水动力。李辉等［5］运用兴波阻力、粘性阻力、锚链力等公式计算了限制水域的船舶纵向下水。高岚虹等［6］运用轴向粘性力模型计算了水阻力。总体来说，这类问题研究的复杂之处主要在于瞬时湿表面难以确定，压力及阻力积分困难；水动力模型需要考虑的因素较多，计算量较大。

第2类问题则是将船舶下水视为一个静力学问题。考虑到船舶下水过程速度并不大，忽略流体粘性阻力以及流体与船体的相互作用，从而将船舶下水简化为静力学过程。对于这类问题的研究方法，经典教科书做了较为详尽的介绍［1］。在此基础上，顾永宁［7］提出了船舶弹性下水计算方法，为传统邦戎曲线法的应用补充了对支墩力学行为等方面的考虑。钟骏平等［8］采用类似的方法分析了船舶下水全过程的受力历程。综合而言，这类问题的分析方法沿用了邦戎曲线法的主体思想来计算下水曲线，随后进行下水过程的力学分析。然而，下水曲线的计算较为繁琐，如果邦戎曲线站数划分较少，则迭代精度将不会很高，下水曲线计算的误差可能会严重影响对船舶下水安全性的评估以及后续的一系列力学分析。因此，在第2类问题的研究中，快速、准确地计算纵向下水曲线就显得尤为重要。

本文将基于第2类问题，提出采用下水曲线直接计算法以替代传统的邦戎曲线法，从而克服邦戎曲线法在下水过程分析中的困难。将以驳船和Wigley船型为分析对象，采用直接计算法对下水曲线进行计算，得到与传统邦戎曲线法一致的结果，以表明该方法的准确性。用实践证明所提出的直接计算法可以处理复杂船型，具有网格尺寸不敏感、普适性强等特点。

1　纵向下水曲线直接计算法

1.1直接计算法原理

纵向下水曲线直接计算法首先需要建立船体外表面有限元模型，用有限元面元积分计算瞬时湿表面上的水压力总和，用牛顿迭代法计算艉浮之后各个时刻的倾角。本文选取ABAQUS中的AQUA模块来施行直接计算法。

船体外表面采用ABAQUS中的R3D3与R3D4刚性面单元进行建模。当船舶重心确定后，用C3D8实体单元作为等效重力单元。船舶艏支点一般指定为面单元与重力单元的运动参考点，此处将艏支点假定在距船艏1/10船长处。在艉浮之前，运动主要是平动；在艉浮之后，解除转动方向的约束，ABAQUS将自动进行牛顿迭代，计算出模型平衡状态。ABAQUS能够输出参考点的受力，包括x，y，z方向的3个支反力RF1，RF2和RF3，以及绕x，y，z方向的3个支反力矩RM1，RM2，RM3。一艘方形驳船的直接计算法模型如图1所示。

针对该方形驳船，根据参考点输出的支反力及支反力矩，经过各个状态的静力平衡分析，通过

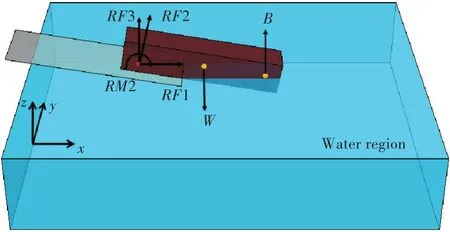
图1直接计算法模型Fig.1 Model of direct calculation method

式（1）～式（6）的计算，能够得出绘制曲线所需的数据。

式中：W为船舶重力；m为船舶质量；g为重力加速度；MW为对艏支点的重力矩；MW'为对滑道末端重力矩；B为浮力；MB为对艏支点的浮力矩；MB'为对滑道末端的浮力矩。纵向下水曲线主要反映这6个量与滑程之间的关系。此外，式中：L为型长；θ为船舶倾角；D为型深；S为初始状态艏支点与滑道末端的距离；x为滑程；α为滑道倾角。完成式（1）～式（6）的计算之后，可以绘出相应的6条下水曲线。

1.2直接计算法准确性验证

本文采用几何形状简单的方形驳船进行直接计算，得出其下水曲线，并与邦戎曲线法的结果进行对比，以验证方法的准确性。

方形驳船型长100 m，型宽20 m，型深20 m。下水滑道倾角为10°，艏支点距船艏1/10船长。直接计算法与邦戎曲线法计算得到的下水曲线如图2所示。

需要特别注意的是，为了使6条下水曲线比例合理，B值与W值均人工放大了20倍。

从图2可以看出，直接计算法结果与邦戎曲线法结果吻合很好。

下面，再利用直接计算法计算不同滑道倾角与不同相对水面高度下方形驳船的下水曲线。

图3所示为滑道倾角分别为5°，10°和15°时方形驳船的下水曲线。图4所示为水面相对船台末端高度分别为-5，0和5 m时方形驳船的下水曲线。

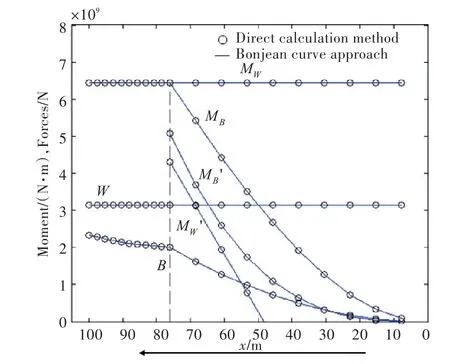
图2方形驳船直接计算法验证Fig.2 Checking for direct calculation method on the box barge

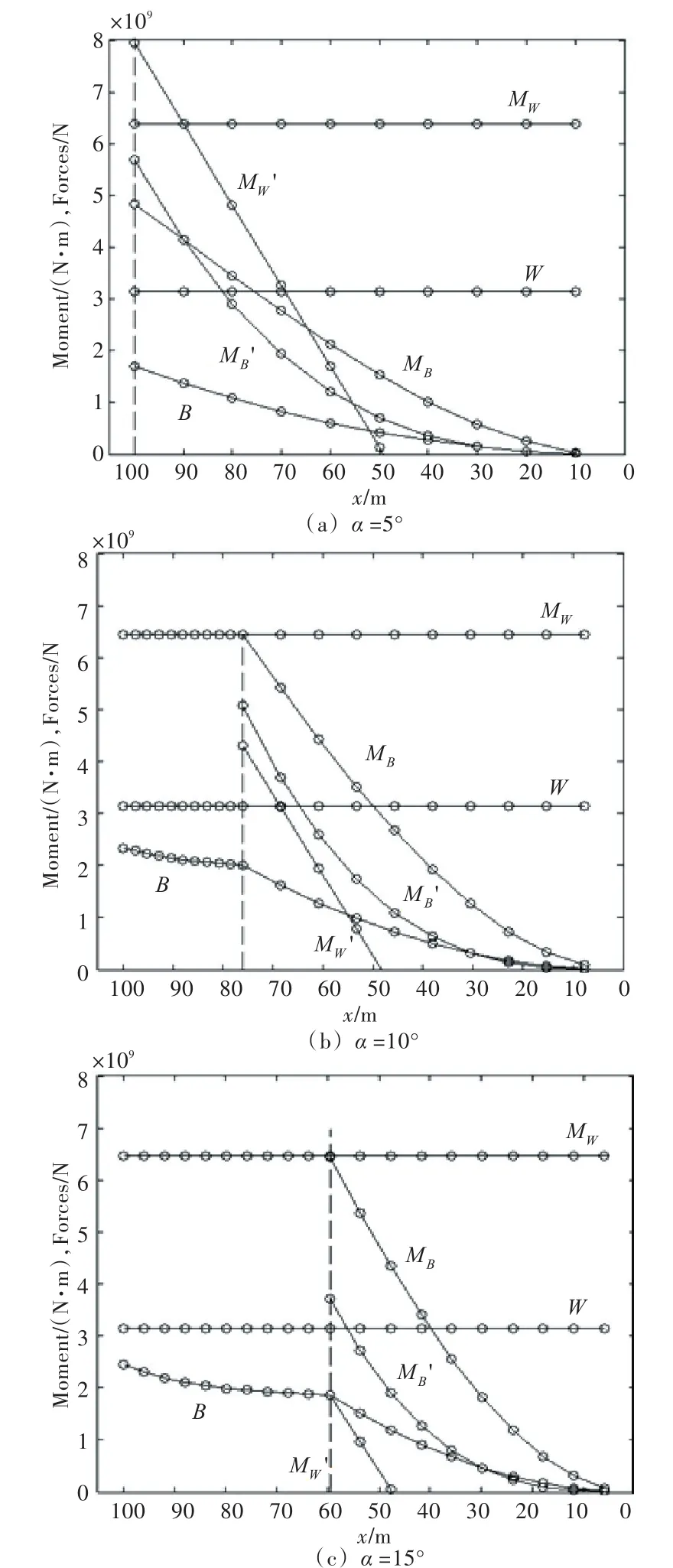
图3 3个不同滑道倾角对应的下水曲线Fig.3　 Launching curves of three different slipway trim angles with 5°，10°and 15°

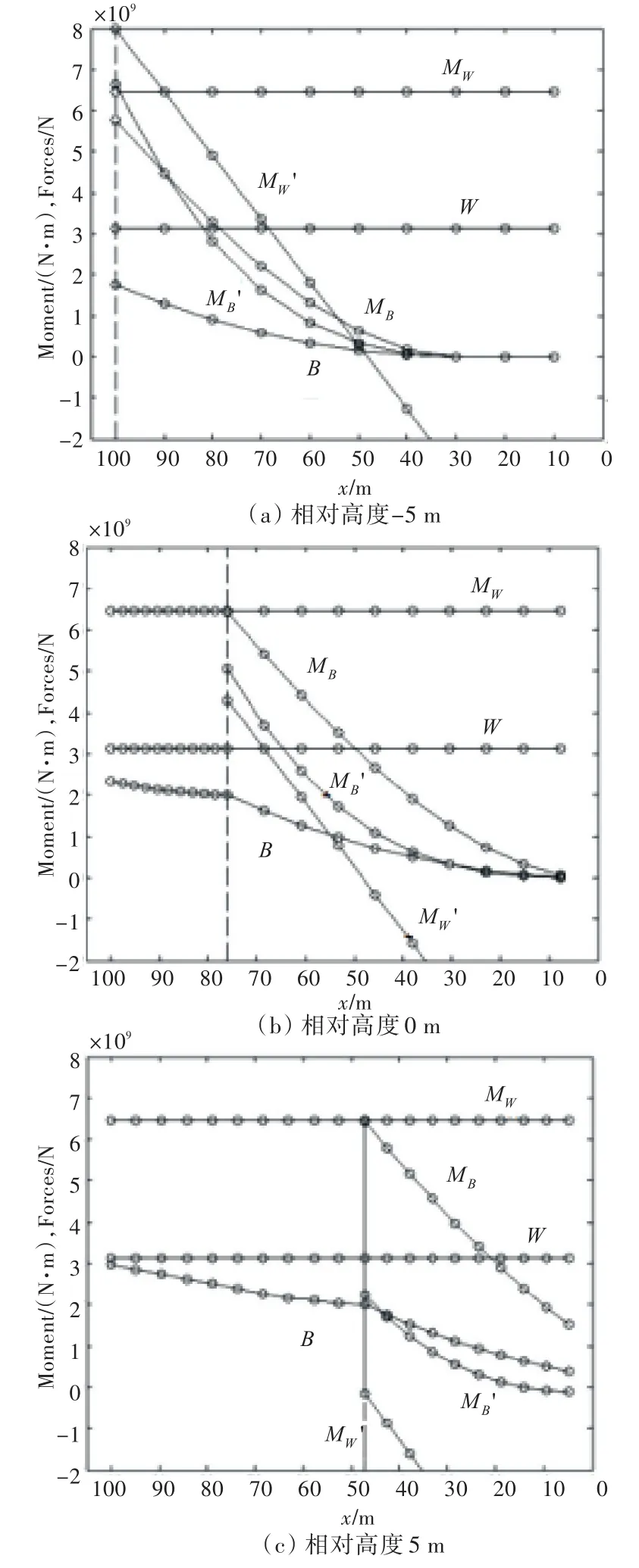
图4 3个不同相对高度对应的下水曲线Fig.4　 Launching curves of three different height with -5 m，0 m and 5 m

图3（a）中，MW'曲线与MB'曲线相交就意味着会发生艉落现象。发生艉落时，滑道末端的应力集中现象较为严重，可能会导致船身或是船台的损坏，应予以避免。图3（b）与图3（c）中MW'曲线与MB'曲线均不相交，但在整个滑程范围内，B均小于W，这会导致艏落现象，船艏会碰击船台末端，从而发生危险。

图4（a）中，MW'曲线与MB'曲线有交点，会发生艉落现象。而图4（c）中，在滑动结束时，B曲线与W曲线相交，恰好不会发生艏落现象。

从以上分析可以总结出，当滑道倾角过小，水面高度过低时，可能会发生艉落或艏落事故。因此，适当加大倾角，以及在涨潮时下水，有利于船舶纵向下水的安全性。

综合而言，针对方形驳船的下水曲线计算，直接计算法与邦戎曲线法的结果差异很小；而有关各因素对下水影响的分析与经典教科书内容也基本一致［1］，因此，可以认为直接计算法是准确的。

事实上，直接计算法主要是运用商用软件ABAQUS构建船舶下水的有限元模型，船体表面静水载荷由ABAQUS/AQUA模块准确定义，运动分析模式主要为静力学分析。从载荷与运动这2个方面来看，直接计算法与传统的邦戎曲线法基本一致，因此，二者的计算结果吻合较好。

另外，值得注意的是，在传统邦戎曲线法的应用中，改变坡道倾角、水面相对船台高度等因素可能需要进行较多的重复性计算，造成人力的浪费；而直接计算法以商用有限元软件为计算后台，更改参数则相对更为简便，且计算程序能够重复使用；因此，直接计算法的灵活性较强。

1.3直接计算法网格敏感性分析

纵向下水曲线直接计算法的计算后台是商用有限元软件ABAQUS，因此，网格敏感性必为其重要的评估指标之一。

图5所示为用稀疏网格、中等密度网格和密网格对一艘驳船进行直接计算法建模后的图示。用直接计算法得出的3种不同网格密度模型的下水曲线如图6所示。

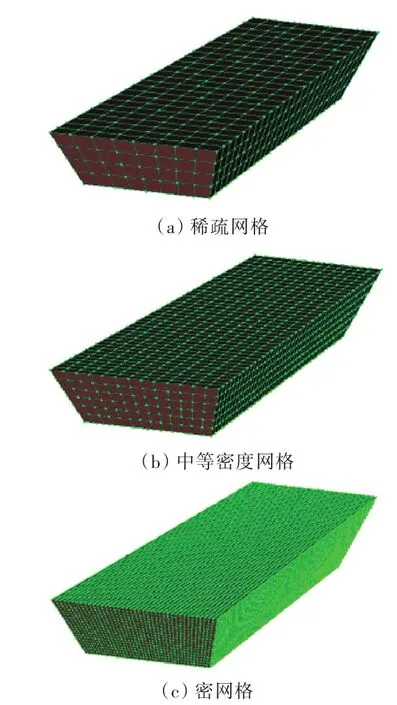
图5驳船的直接计算模型Fig.5 Direct calculation models of barge with sparse mesh，mid-dense mesh and dense mesh

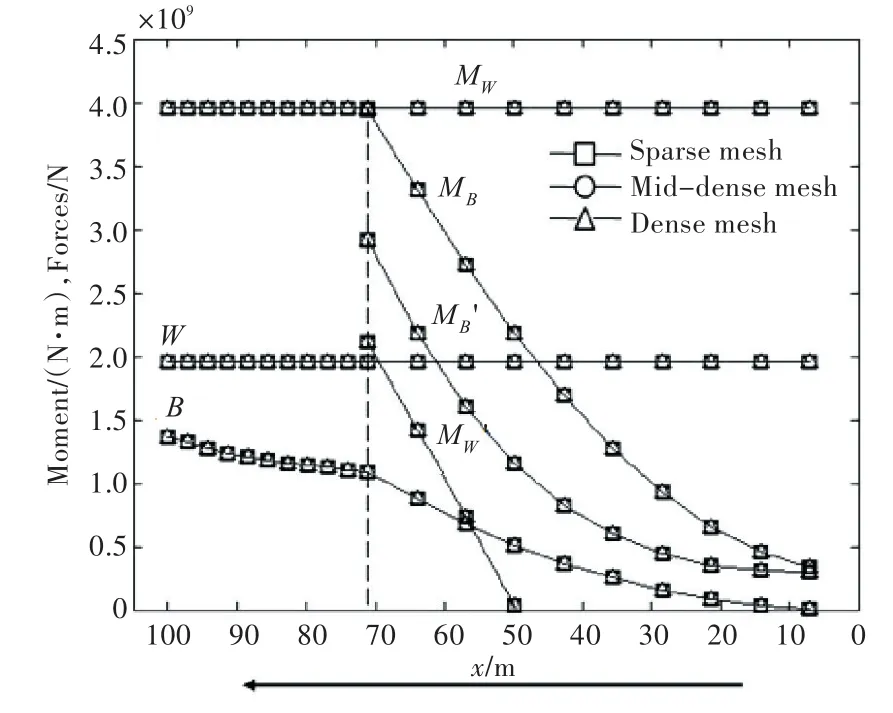
图6不同网格密度驳船直接计算法得出的下水曲线Fig.6　 Launching curves of three barge models with different meshes

与方形驳船不同的是，此驳船模型在长度、宽度和高度3个方向均具有较大的型线变化。就传统邦戎曲线法而言，对其划分站数越密，计算结果将越精准。然而，从图6可以看出，用直接计算法得出的3种网格密度的下水曲线几乎完全一致。因此，原则上可以认为，直接计算法对网格密度是不敏感的。出于节约计算量的目的，当模型网格足以准确反映下水船舶几何外形时，网格密度越小越好。

2　船型算例

2.1 Wigley船下水曲线直接计算

驳船由于几何外形简单，无法充分说明直接计算法的可行性与普适性。本文选取易于验证的Wigley数值船型（图7）进行直接计算，将得到的下水曲线与邦戎曲线法的结果进行比较，以证明直接计算法的可行性与普适性。

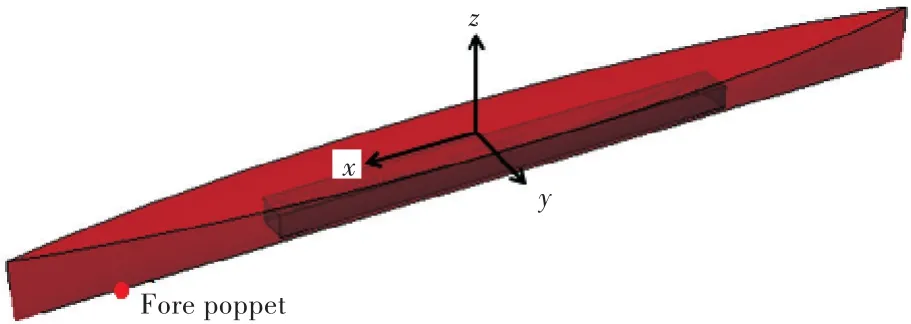
图7 Wigley船直接计算模型Fig.7 Direct calculation model of the Wigley ship

选取的Wigley数值船型长L为120 m，B为型宽10 m，型深D为7.5 m，其外表面由式（7）决定。计算模型单元数为15 849，平均单元尺寸为0.5 m。

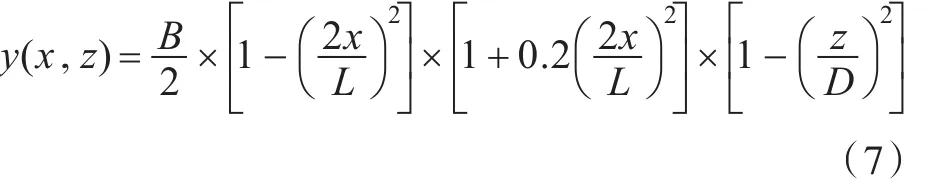
下水滑道倾角α=5°，艏支点距船艏1/10船长。2种方法计算的下水曲线如图8所示。

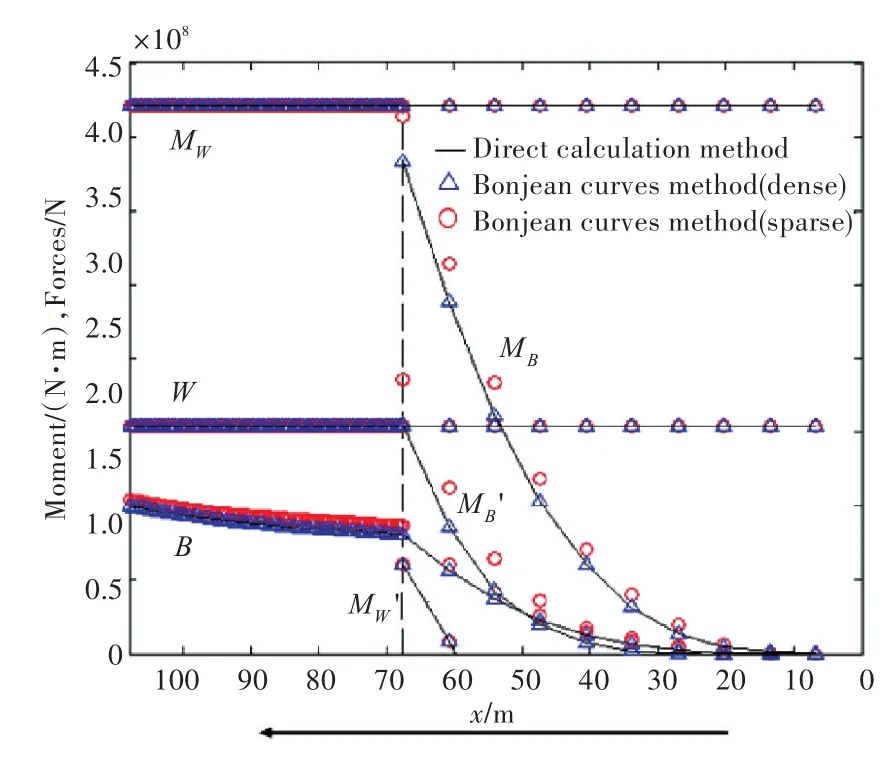
图8 Wigley船直接计算法验证Fig.8 Checking for direct calculation method on the Wigley ship

需要特别注意的是，为了使6条下水曲线比例合理，B值与W值均人工放大了20倍。

经过ABAQUS的后处理，Wigley船各个时刻的下水状态如图9所示。

从图8可以看出，采用直接计算法计算的下水曲线与邦戎曲线法计算的下水曲线差异较小。并且，图8中，随着划分站数的增多，邦戎曲线解收敛于直接计算法解。可见，直接计算法是能够计算变曲率复杂表面船舶的下水曲线的，因而具有较好的可行性与普适性。

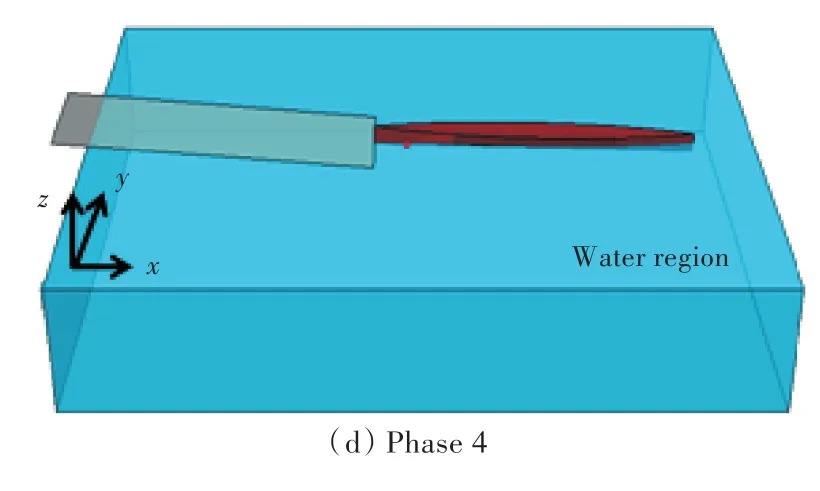
图9 Wigley船下水各状态Fig.9　 Different launching phases of the Wigley ship

2.2油船下水曲线直接计算

本文采用直接计算法计算46 000 t DWT油船的下水曲线。该油船型长182 m，型宽32 m，型深21 m，下水滑道倾角α=5°，艏支点距船艏1/10船长。油船的直接计算模型如图10所示，模型单元数为30 112，平均单元尺寸为0.85 m。

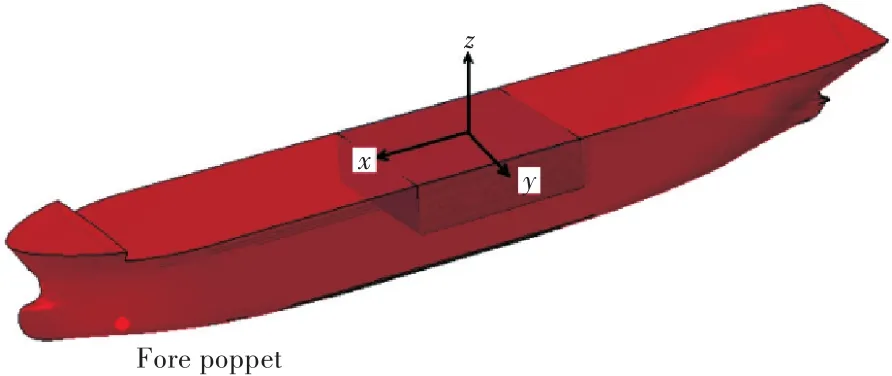
图10 46 000 t DWT油船直接计算模型Fig.10　 Direct calculation model of the 46 000 t DWT tanker

由直接计算法得出的纵向下水曲线如图11所示，下水过程的各个运动状态如图12所示。需要特别注意的是，为了使6条下水曲线比例合理，B值与W值均人工放大了50倍。另外，MW'曲线并没有显示在下水曲线中，这是因为MW'在整个下水过程中均为负值，没有绘出的必要。

图11 46 000 t DWT油船直接计算法计算的下水曲线Fig.11 Launching curves of the 46 000 t DWT tanker

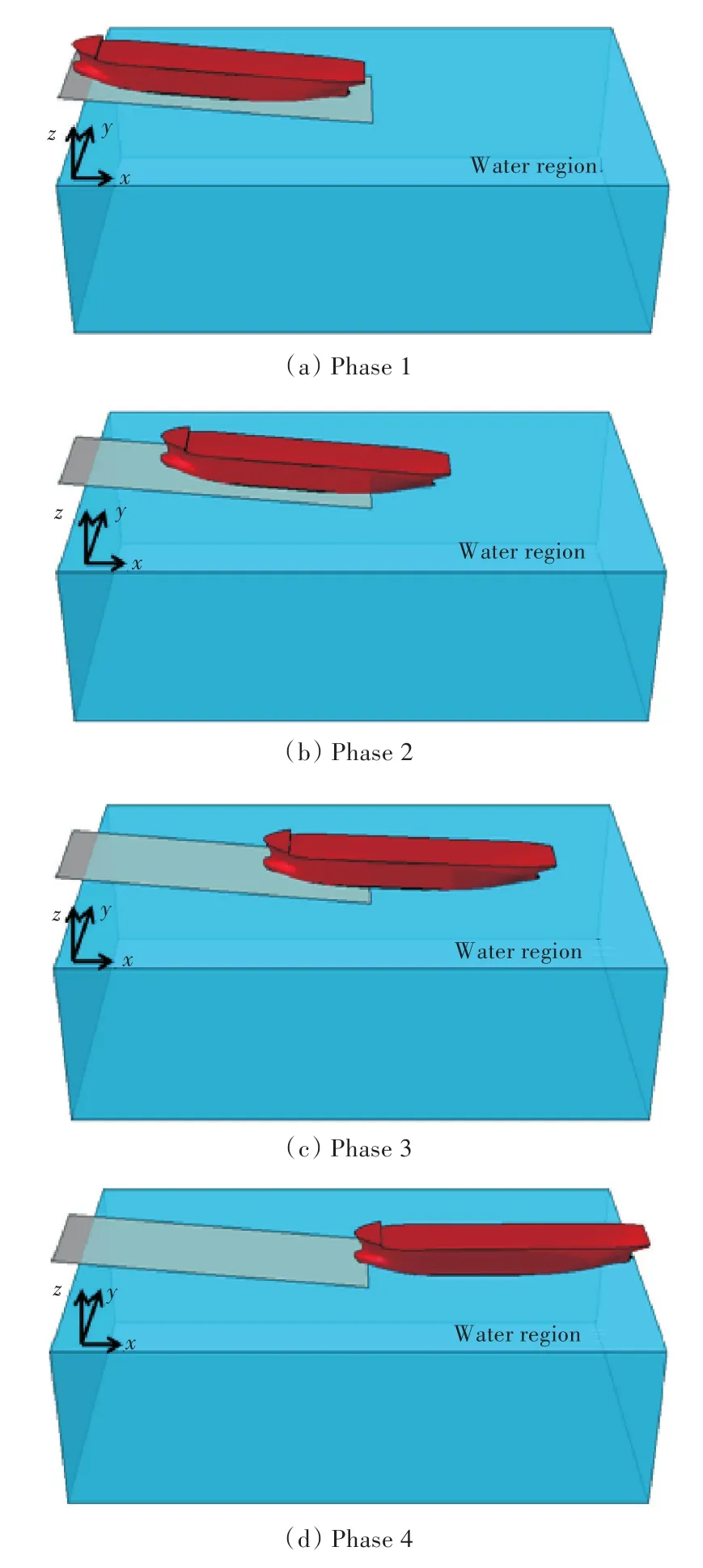
图12 46 000 t DWT油船下水各状态Fig.12 Different launching phases of the 46 000 t DWT tanker

由图11可以看出，MW'曲线与MB'曲线没有交点，B曲线与W曲线相交，下水过程既不会出现艉落，也不会出现艏落。大约在滑程185 m处，船艏能够顺利上浮。因此，根据下水曲线，可以认为该46 000 t DWT油船能够安全下水。

3　结　论

本文提出的船舶纵向下水直接计算法具有以下特点：

1）针对方形驳船，用直接计算法得到的下水曲线与传统邦戎曲线法得到的结果相互吻合，表明了直接计算法的准确性。

2）原则上讲，船舶纵向下水直接计算法对网格尺寸是不敏感的；而邦戎曲线法与分站数量有关，随着分站数的增多，邦戎曲线解收敛于直接计算法的解。

3）本文中所有的计算均在配备2.50 GHz CPU与4.00 GB RAM的计算机上运行。方形驳船、Wigley数值船型和油船的计算CPU耗时分别为1.1，43.2和194.7 s，计算效率高。

4）本文采用的直接计算法是以商用软件ABAQUS为后台，所用的单元为刚性面单元，施加的载荷为简单的静水载荷，运动分析模式为静态分析。一般的商用有限元软件均具备实施这一方法的能力，因此，直接计算法具有一定的可行性与通用性。

5）与传统的邦戎曲线法相比，直接计算法能够计算复杂外形船舶的下水曲线，流程简洁灵活、可重复性强，并且能够直观显示下水过程中的船舶状况，具有较好的普适性。

因此，本文提出的船舶纵向下水曲线直接计算法具有潜在的工程应用价值。

参考文献：

［1］TUPPER E C. Introduction to naval architecture［M］. 4th ed. Amsterdam：Elsevier Butterworth-Heinemann Linacre House，2004.

［2］吴晶.船舶下水动态过程数值模拟分析研究［D］.大连：大连理工大学，2009.

［3］王文华，王言英.基于CFD方法的船体下水水动力分析［J］.大连海事大学学报，2009，35（3）：1-4. WANG Wenhua，WANG Yanying. Dynamic analysis for ship launching based on CFD method［J］. Journal of Dalian Maritime University，2009，35（3）：1-4.

［4］王文华，王言英.船台及船体各状态参数对船舶下水运动的影响［J］.中国造船，2009，50（3）：84-92. WANG Wenhua，WANG Yanying. Effect of status pa⁃rameters of slipway and hull on motion of ship launch⁃ing［J］. Shipbuilding of China，2009，50（3）：84-92.

［5］李辉，于辉，李学菊，等.限制水域船舶纵向下水的动力学分析［J］.中国造船，2009，50（4）：61-66. LI Hui，YU Hui，LI Xueju，et al. Dynamic analysis of longitudinal ship launching in restricted water［J］. Shipbuilding of China，2009，50（4）：61-66.

［6］高岚虹，叶家玮.船舶纵向重力式下水的预测模型［J］.船舶，2000（2）：19-22. GAO Lanhong，YE Jiawei. Prediction model for longi⁃tudinal gravity launching of ship［J］. Ship and Boat，2000（2）：19-22.

［7］顾永宁.船舶纵向下水弹性计算方法和结构安全性［J］.上海交通大学学报，1996，30（10）：104-110. GU Yongning. The elastic calculation of ship longitudi⁃nal launch and structural safety［J］. Journal of Shang⁃hai Jiaotong University，1996，30（10）：104-110.

［8］钟骏平，程远胜，刘均，等.基于ANSYS的船舶纵向下水弹性计算方法［J］.船舶力学，2007，11（5）：752-758. ZHONG Junping，CHENG Yuansheng，LIU Jun，et al. Elastic calculation of ship end launching using AN⁃SYS［J］. Journal of Ship Mechanics，2007，11（5）：752-758.

A direct calculation method for ship longitudinal launching curves

LIN Shiyao1，SUN Jianglong1，2，3，ZENG Jingzhou1，XIE De1，2，3

1 School of Naval Architecture and Ocean Engineering，Huazhong University of Science and Technology，Wuhan 430074，China
2 Hubei Key Laboratory of Naval Architecture and Ocean Engineering Hydrodynamics，Wuhan 430074，China
3 Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration，Shanghai 200240，China

Abstract：In this paper, a direct calculation method is proposed to obtain the launching curves of ship lon⁃gitudinal launching. Specifically, the outer surface of ships is assumed as rigid elements, and commercial FEA software ABAQUS/AQUA is applied for the direct calculation of ship longitudinal launching curves. This method is then studied on a box barge and the outputs of launching curves are compared to those ob⁃tained by traditional methods based on Bonjean curves with excellent agreements. In addition, with regard to a barge with relatively complex geometry, the proposed method is shown to be insensitive to mesh sizes. All these features demonstrate the accuracy and efficiency of the direct calculation method proposed in this paper. Finally, the method is applied to a Wigley type and a tanker to verify the feasibility and the suitabili⁃ty, which indicates that the direct calculation method has a great potential to solve engineering problems on different ship launching.

Key words：longitudinal launching；launching curves；direct calculation method；Bonjean curves meth⁃od；ABAQUS/AQUA

作者简介：林诗尧，男，1992年生，硕士生。研究方向：船舶与海洋工程直接计算法。E-mail：shiyao_lin@hust.edu.cn解德（通信作者），男，1964年生，博士，教授，博士生导师。研究方向：船舶与海洋结构物设计制造。E-mail：dexie@hust.edu.cn

基金项目：国家自然科学基金资助项目（51079059）

收稿日期：2015 - 03 - 18网络出版时间：2016-1-19 14:55

中图分类号：U671.5

文献标志码：A

DOI：10.3969/j.issn.1673-3185.2016.01.017

网络出版地址：http://www.cnki.net/kcms/detail/42.1755.TJ.20160119.1455.006.html期刊网址：www.ship-research.com

引用格式：林诗尧，孙江龙，曾荆州，等.船舶纵向下水曲线直接计算法［J］.中国舰船研究，2016，11（1）：128-134. LIN Shiyao，SUN Jianglong，ZENG Jingzhou，et al. A direct calculation method for ship longitudinal launching curves ［J］. Chinese Journal of Ship Research，2016，11（1）：128-134.