混凝土板在接触爆炸作用下的震塌和贯穿临界厚度计算方法*

岳松林，王明洋，张 宁，邱艳宇，王德荣

(解放军理工大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007)

混凝土板在接触爆炸作用下的震塌和贯穿临界厚度计算方法*

岳松林，王明洋，张 宁，邱艳宇，王德荣

(解放军理工大学爆炸冲击防灾减灾国家重点实验室,江苏 南京 210007)

采用刚塑性模型描述介质的动力学行为，结合不可压缩条件和质量守恒条件及边界条件，构造塑性区的动力学许可速度场；利用极限平衡原理推导动力学许可速度场所对应的介质抗力的量纲一表达式；根据初始条件和边界条件，求解运动方程，分别得到爆炸震塌的临界厚度和爆炸贯穿的临界厚度，并推得能够反映爆炸源参数和材料参数综合性质的量纲一冲击因子。将推得的计算公式与经验公式对比分析，证明本文计算结果合理，推导的计算公式揭示了经验公式的物理本质，且具有较为广泛的适用范围。

爆炸力学；临界厚度；刚塑性模型；极限平衡原理；接触爆炸；震塌；贯穿；量纲一冲击因子

混凝土板在爆炸或冲击作用下，将产生震塌、贯穿以及冲切等形态的局部破坏，关于这些局部破坏效应的问题称为震塌问题[1-2]。震塌破坏是指结构体受到爆炸或冲击荷载作用时，在结构背面形成反射拉伸波，并造成结构背面介质的破碎和层裂。贯穿破坏是结构厚度相对较薄情形下，爆炸或冲击荷载产生的压缩弹坑与背爆面震塌坑贯通，形成贯穿的孔洞。冲切破坏是结构厚度很小的情况下，爆炸或冲击荷载将作用范围内靶板材料整体冲塞下来，在靶板中不能区分压缩弹坑和震塌坑。爆炸震塌和爆炸贯穿是指爆炸荷载导致的震塌破坏和贯穿破坏，区别于冲击或侵彻震塌和贯穿[3]。由于混凝土是一种结构性材料，其强度和变形特性受配合比、骨料尺寸等材料结构特性的影响，因此混凝土材料的震塌破坏既与金属材料的震塌破坏有相同的机理，又有自身的特点。尤其是结构性材料的随机分布、钢筋与混凝土的相互作用等复杂问题尚待解决。因此混凝土材料的结构震塌问题的理论研究进展缓慢[1]。

震塌破坏现象最早是由霍普金森于1914年进行爆炸效应研究时观察到的；随后，莱茵哈特在金属板接触爆炸的实验中，曾多次观察到层裂现象，他将爆炸荷载简化为三角形荷载，并用第一强度理论计算出了层裂厚度和剥离速度；20世纪60年代后期，美国弹道研究实验室(Ballistic Research Laboratory)提出了BRL公式，可以直接计算贯穿厚度，通过实验研究得到震塌厚度与贯穿厚度间的关系[3]；20世纪70年代，格伦、B. C. 尼基福罗夫斯基和Е.И. 舍马金亦分别采用第一强度理论和三角形荷载的假设，得到爆炸震塌的相关研究成果[3]。1982年，A.Haldar等[4]根据量纲分析，用外部荷载总能量与介质抗压强度间的关系，引入量纲一参数：I=(NmV2)/(D3fc)；1984年，G.Hughes[5]利用外部荷载总能量与混凝土的抗拉强度之间的关系，定义冲击系数如下：I=(NmV2)/(D3ft)。然而这些研究成果多数是关于弹体冲击或侵彻引起的震塌和贯穿效应，关于爆炸震塌方面的资料很少，仅有美国空军《防护结构设计手册》给出了爆炸震塌厚度经验公式，被称为PCDM公式[1]，但PCDM公式不适用于接触爆炸对防护结构的破坏作用。

20世纪50～70年代，中国曾系统地组织关于结构体遭受炮航弹攻击时的震塌破坏实验，基于大量的实验数据，编制了相关的设计规范。但限于实验设备和测量手段落后，获取的有效信息较少，因而对震塌破坏的认识尚处于宏观唯象阶段，现行设计规范中给出的震塌半径计算公式，只能给出近似预测值，与当前发展和应用新型防护材料的需求不相适应[3]。近年来，中国学者对爆炸近区问题和爆炸震塌机理的研究更加深入，提出了一些更加适用的震塌计算公式和防护结构设计方法,如：王明洋等[6]提出在研究介质中侵彻与爆炸近区过程中，运用空腔膨胀理论存在的问题，分析了其产生的原因，并推得侵彻、贯穿比例换算关系和爆炸近区的几何相似关系等简单实用的结果；王明洋等[7]给出了钢板-钢纤维钢筋混凝土遮弹板接触爆炸下的极限设计分析的实用方法；张想柏等[2]进行了混凝土板表面接触爆炸实验，运用相似理论和数值手段，对爆炸震塌实验数据和现象进行分析，基于量纲分析建立了新的震塌厚度计算公式，并根据破坏等级，将震塌破坏系数定量化；王德荣等[8-9]和李学业等[10]结合爆炸近区运动学关系式和径向裂缝阵面形成时的耗能情况，研究爆炸近区介质的动力变形与破坏情况，得到RPC混凝土在接触爆炸作用下的破坏半径系数。这些工作注重对震塌破坏的物理机理和力学本质的研究，对震塌效应评估和防护结构设计有重要的参考价值，然而这些成果不能有效区分震塌破坏、贯穿破坏和冲切破坏。

根据冲击震塌和贯穿方面的研究成果[11-14]，本文中把临界震塌厚度和临界贯穿厚度作为评估爆炸局部破坏的2个分界点。爆炸荷载固定的情况下，当材料厚度大于临界震塌厚度时，只在结构迎爆面产生压缩弹坑，不会发生震塌现象；当材料厚度介于临界震塌厚度和临界贯穿厚度时，发生爆炸震塌现象；当材料厚度小于临界贯穿厚度时，发生爆炸贯穿现象；当材料厚度足够小时，计算得到的临界震塌厚度等于或小于临界贯穿厚度，它代表材料尚未形成震塌块就被整体冲切下来，此时发生爆炸冲切现象。因此，问题的关键是如何确定爆炸作用下板的临界震塌厚度和临界贯穿厚度。本文中结合理论分析，推导2类临界厚度的计算公式，并进行算例和对比分析。

1 基本原理及模型假设

建立介质表面点源爆炸的物理模型，研究混凝土板在接触爆炸作用下的局部破坏现象。根据混凝土板爆炸局部破坏效应实验[2-15]，在板厚足够大的情况下，板的迎爆面，产生压缩弹坑，可不考虑反射面的影响；随着板厚的减小，板的背爆面，即反射面，开始出现明显裂纹、鼓包，甚至产生反射漏斗坑，发生震塌现象；板厚进一步减小，反射漏斗坑与压缩漏斗坑贯通，发生贯穿现象；当板厚足够小，迎爆面尚未形成压缩弹坑，板已经被击穿，此种情况为板的冲切现象。

从能量的角度来讲，混凝土材料在爆炸荷载作用下发生屈服破碎，碎块相互摩擦、滑动，这是对爆炸能量消耗的过程，塑性阶段消耗的能量远大于弹性阶段消耗，可忽略弹性阶段；而爆炸近区出现不可逆的大变形，自由面存在的情况下，应变球张量(体积压缩量)很小和应变偏张量(剪切变形量)很大，在整个应力应变曲线上，塑性阶段为主要部分，弹性阶段可以忽略，因此采用刚塑性模型描述介质的动力学行为[13]。

根据不可压缩条件和质量守恒条件及边界条件，构造塑性区的动力学许可速度场；利用极限平衡原理分别推得半空间介质表面和有限厚度介质表面压缩弹坑在膨胀过程中的介质抗力的量纲一表达式。根据冲击阻力的量纲一表达式，可以得到冲击阻力曲线，进而能够找到临界震塌的压碎区半径RA和临界贯穿的压碎区半径RB。结合初始条件，对膨胀过程的运动方程积分，可以计算得到最终的压碎区半径R。如果R=RA，则在此板厚和装药情况下发生临界震塌现象，此时的板厚LA为临界震塌板厚；如果R=RB，则在此板厚和装药情况下发生临界贯穿现象，此时的板厚LB为临界贯穿板厚。

如果已知介质抗力P，可得运动方程：

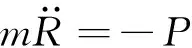
(1)

式中：m为冲击体质量；R为压碎区半径。冲击体的初始条件为：

(2)

式中：a为冲击体的初始半径，v0为初始径向冲击速度。结合式(2)可以求出压碎区最终半径R，然后比较R、RA、RB的关系，可以判定在板厚L条件下发生何种破坏现象。

通过求刚塑性模型的极限荷载可以得到介质抗力P。介质的极限荷载是材料开始发生塑性变形时的荷载。对于刚塑性模型，可得到极限荷载的上下限。根据虚功率原理和塑性极限荷载上限定理有[16-18]：

(3)

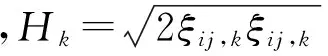
(4)

根据式(4)右侧积分量，求左侧未知极限荷载Pi,k，从上限来评估极限作用力。这样，问题的关键在于如何建立动力学许可速度场，而这一描述可以通过实验数据和过程的实验室模拟来获得[18-19]。

2 爆炸抗力极限载荷值计算

2.1 冲击体初始条件

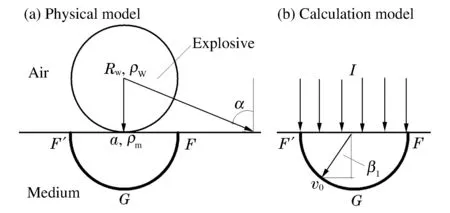
图1 接触爆炸下介质表面冲量荷载计算模型Fig.1 Impulse on the surface of medium under contact explosion

图1为接触爆炸下介质表面冲量计算模型，Rw为装药半径，ρw为装药密度，ρm为介质密度，α1介质表面一点到装药中心点的连线与介质表面发现的夹角，β1为压碎区边界上一点与压碎区球心的连线。假设爆炸为瞬时爆轰，球形装药与介质表面接触；爆轰产物对介质高速冲击作用下，介质剪切模量可以忽略，区域FGF′瞬间进入塑性流动状态；区域FGF′的半球体为初始冲击体，且爆轰产物对介质的冲量全部转化为初始冲击体的动量。

根据文献[20]，介质表面接触爆炸荷载冲量为

I=uxQμ′=πA0Qsin2α1

(5)

式中：μ′为药形系数，Q为装药质量，A0=(Nxw+ux)/(4π)，Nxw=Pw/(ρwux)，Pw=Ps=PD/2=(ρwD2)/2(k+1)，ux≈(2Qv)1/2，Q=πRw3ρw/3，Pw为平均爆轰压力，PD为爆轰波阵面压力，Qv为比能量或爆热，ux为爆轰产物喷流或散射速度，Nxw为喷流面或散射面的移动速度，D为爆速。

根据动量守恒定律：压力冲量等于动量的变化，爆轰产物的竖向冲量等于冲击体竖向动量的初始值

(6)

式中：m=2πρma3/3，为初始冲击体的质量，即区域FGF′的质量。

假设板的特征尺度远大于炸药中心到板的距离l，则α=π/2，I=πA0Q，因此初始冲击体的动能为

(7)

又由功能转换原理，建立初始冲击体动能与药量的关系[28-30]：

(8)

(9)

TNT的爆热Qv=4.23×106J/kg，其爆炸产物的平均喷流速度：ux=2 908 m/s；爆轰波阵面压力PD=1.77×1010Pa，平均爆轰压力Pw=8.83×109Pa，ρw=1 600 kg/m3，ux=2 908 m/s；已知岩石的密度约为ρ1=2 600 kg/m3，松散砂土的堆积密度约为ρ2=1 600 kg/m3。将这些参数代入式(9)中，可以分别算得岩石表面爆炸和松散砂土表面爆炸的能量分配系数：η1=0.21；η2=0.34。根据文献[20]中的计算结果：药包底部位于地表面时，表面爆炸能分配系数η=0.22，它介于本文计算结果中间，即η1<η<η2，能够从一定程度上证明本文采用的冲量计算模型是合理的。

2.2 厚板表面点源爆炸的抗力计算

图2 半空间表面点源爆炸介质区域划分Fig.2 Regional division of the half-space medium subjected to point-source explosion

当板的厚度足够大时，接触爆炸荷载作用下，迎爆面产生压缩弹坑，背爆面无明显变化，其物理模型为半空间介质表面点源爆炸。本文中采用刚塑性模型描述，其压碎机理为剪切破坏，相关计算方法参见式(3)，根据爆炸实验现象，可以如图2所示构造动力学许可速度场，介质被分成3个区域(I、II、III)。

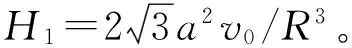
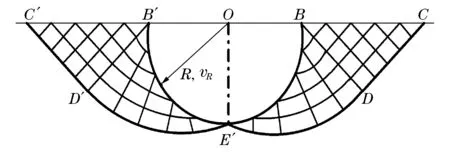
图3 区域II、III速度场Fig.3 Velocity fields in regions II and III

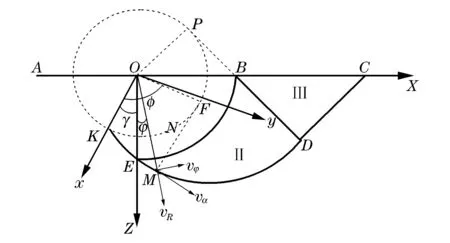
图4 塑性区II、III边界曲线Fig.4 Schematic boundary lines of plastic regions

x=rcosφ+rφsinφ,y=rsinφ-rφcosφ

(10)

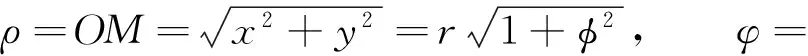
(11)

将塑性区域绕Z轴旋转，可以得到球坐标中的塑性体，记旋转角为θ，结合以上条件，可以得到球坐标(ρ,φ,θ)下各个区域的速度场。区域II动力学许可速度场为

(12)

应变率场为

(13)

剪应变率强度为

(14)

区域III速度场的直角坐标形式为

vZ,3=-vR，vX,3=vR，vθ,3=0

(15)

应变率场为

ξZ,3=ξX,3=ξθ,3=0

(16)

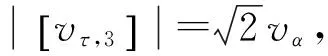
将上文计算得到的各物理量代入式(4)，得半空间表面点源爆炸过程中介质抗力的量纲一形式为

(17)

2.3 有限厚度板表面点源爆炸的抗力计算

图5 有限厚度板表面点源爆炸介质区域划分Fig.5 Regional division of the limited thickness slab subjected to point-source explosion

有限厚度板表面点源爆炸时，靶体背爆面的影响是显著的，压碎区半径R发展到一定程度时靶体材料停止向迎爆面挤出，而开始向背表面移动，图5是有限厚度板表面点源爆炸介质区域划分示意。区域I是爆炸源周围的压碎区，区域II是背表面反射拉伸波产生的破碎区，区域III是弹性变形区(可忽略其变形和位移)。

2.3.1 动力学许可第1速度场

图4中区域II的范围为

0≤φ≤φ0=π/4,R≤r≤L

(18)

压碎区壳体的区域为

Σ1:x2+y2+z2=a2,Σ2:x2+y2+z2=R2

(19)

Σ1范围内椎体体积为

(20)

Σ1范围内椎体的锥底面积为

(21)

Σ2范围内椎体体积为

V2=2πR3(1-cosφ0)/3

(22)

Σ2范围内椎体的锥底面积为

S2=2πR2(1-cosφ0)

(23)

(1)根据质量守恒，设vr为径向速度，其表达式为

(24)

根据不可压缩性条件以及区域对称性，有

(25)

(2)已知速度场，可以得到应变率场：

(26)

(3)应变率强度为

(27)

(4)根据极限载荷上限值原理，经过整理得到介质抗力的极限载荷值：

(28)

2.3.2 动力学许可第2速度场

动力学许可第2个速度场只随时间发生变化，不同位置处介质的速度保持一致，它表示了冲击体直接将漏斗范围内的刚性块体从平板中压出。介质刚性块的运动速度一开始与冲击体速度存在差异，随着运动的发展刚性块速度与冲击体速度相同，由于这个过程十分短暂，这里忽略中间过程，因而刚性块的初始运动速度与冲击体的初始速度同。介质抗力主要是间断面上的摩擦力。

区域II内的速度分量为

vr=vR,vφ=0,vθ=0

(29)

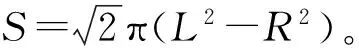
(30)

3 靶板临界厚度计算方法

3.1 爆炸抗力的量纲一化

(31)

有限厚度板表面点源爆炸第1速度场的抗力：

(32)

有限厚度板表面点源爆炸第2速度场的抗力：

(33)

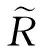
爆炸过程中，冲击接触面上受到周围塑性区的介质抗力总和表达式为

P=Pk·Sr

(34)

式中：Sr为冲击接触面面积。在半空间介质中，不考虑自由面的影响，可以认为Sr=2πr2；在有限厚度介质中，可以认为Sr=2πr2(1-cosφ0)，φ0=π/4。

图6 爆炸抗力的函数曲线Fig.6 Function curves of material resistance

3.2 临界震塌厚度计算方法

根据冲击阻力曲线，可以计算得到介质抗力的极限荷载，结合初始条件求解运动方程就能够计算出压碎区半径，其实质是将波动问题转换为求解抗力的问题。临界震塌情况下，爆炸抗力(P1)和初始冲击体质量(m1)可知。结合方程(1)、(16)、(19)，得到量纲一形式的运动方程：

(35)

初始条件：

(36)

记ω1=6.92πτsa/m1，ω2=11.68πτsa/m1，运动方程变为

(37)

该微分方程不能直接求解，需进行变换形式，分离变量而后积分得

(38)

整理得

(39)

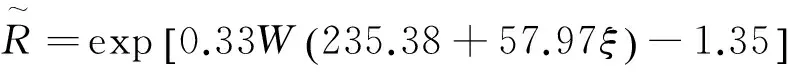
(40)

式中：W为LambertW函数，x>-e-1时，W(x)为递增函数，且结果是单值的实数，因此本文中的W总是单值的实数值。由式(31)、(32)求交点A处的介质厚度得：

(41)

将(40)代入(41)得临界震塌厚度：

(42)

它是量纲一因子ξ的函数，由(5)、(6)可以得到量纲一因子ξ与药包质量Q的关系：

(43)

根据接触爆炸物理模型(如图1)Rw=a，于是ξ=1.73ηQvδρw/τs。根据量纲分析，这是一个多方指数的量纲一组合，它表征了装药密度、炸药爆热、有效能比率、热功当量、介质密度、屈服强度、压力峰值、变形波速、最大粒子速度之间的内在关系。

将量纲一形式的临界震塌厚度，转换为比例距离的形式：

(44)

对于装药参数和介质材料参数确定情况下，量纲一因子ξ是确定的，结合式(42)，该比例距离能够计算。模型尺寸发生改变时，作为震塌与否的判据，它是一个相似常数。对于可忽略重力加速度的小规模地下化学爆炸，这个结果是符合爆炸相似律的。

3.3 临界贯穿厚度计算方法

对于临界贯穿厚度的计算，其初始条件是，冲击阻力曲线图6中A′点所对应的位移和速度。此时冲击体觉察到背爆面(自由面)的存在，并开始形成贯穿体，运动方程中的介质抗力按有限厚度介质中的第1速度场计算，当压碎区半径发展到B′点时，发生贯穿现象，通过B′点处压碎区半径与介质厚度的函数关系，可以计算出临界贯穿厚度。

根据爆炸贯穿的力学模型，结合式(1)、(32)、(34)。可以得到开始形成贯穿体的运动方程：

(45)

初始条件为

(46)

临界贯穿条件为

(47)

式中：t*为贯穿时刻。记ω3=17.63τs/(ρa2)，对式(45)分离变量再积分，得到从初始状态到临界贯穿状态的过程满足

(48)

根据式(38)可以得到开始发生贯穿的初始条件的速度与位移关系：

(49)

结合(48)～(49)，消去vR项，并对其进行整理得到

(50)

根据前文关于ω1、ω2、ω3的定义，可以得到：

ω3/ω1=1.70，ω2/ω1=1.69

(51)

由式(41)可以得到交点A′处初始状态压碎区半径与介质厚度的关系：

(52)

由式(32)～(33)得交点B′可得临界贯穿时压碎区半径与介质厚度的关系：

(53)

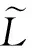
(54)

该方程的根，即能够同时满足贯穿运动方程、初始条件、边界条件的临界贯穿厚度。但无法求得解析解，只能用数值手段求近似解。结合式(44)、(54)可以得到比例距离形式的临界震塌厚度与ξ的关系。

4 算例分析

4.1 两类临界厚度计算分析

图7 临界厚度与无量纲冲击因子的关系曲线Fig.7 Relationship between critical thickness and dimensionless impact factor

图7表明：临界震塌厚度和临界贯穿厚度都是量纲一冲击因子ξ的递增函数，ξ越大临界厚度越大，ξ越小临界厚度越小。量纲一冲击因子是装药密度、炸药爆热、有效能比率、介质屈服强度的综合指标，与爆炸源传给介质的冲击荷载或能量成正比，与介质的强度或抗力成反比。爆炸冲击载荷越强，需要更厚的介质来抵御冲击；介质强度越高，其抗爆炸冲击能力越强，需要的抵抗厚度越小。

经过计算发现：临界震塌厚度Lz约为临界贯穿厚度Lp的2倍，这与BRL公式、修正BRL公式[1,22]中：Lz=2Lp的关系相一致。

4.2 本文分析方法与经验公式的对比

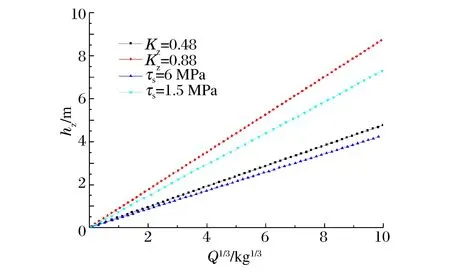
图8 临界震塌厚度与经验公式对比分析Fig.8 Analysis of theoretical and empirical formulas about critical spalling thickness

根据式(44)，可知本文爆炸临界震塌厚度计算公式：

hz=g1(ξ)/(4πρw/3)1/3Q1/3

(55)

式中：hz为震塌临界厚度；g1(ξ)按式(42)计算。

爆炸震塌临界厚度经验公式[1,3,22]如下：

(56)

式中：m*为填塞系数，对于表面爆炸，m*=1.0；Kz为介质材料的临界震塌系数。

利用式(55)～(56)计算临界震塌厚度。将计算结果进行对比，如图8所示。

计算中采用的爆源参数：TNT装药密度ρw=1 600 kg/m3，爆热Qv=4 227 710 J/kg，有效能比率η≈0.21；材料参数：由于临界震塌系数，是根据大量的实验得到的经验参数，这里只能给土工材料的大致范围Kz=0.48～0.88；其对应的介质剪切屈服强度范围为τs=6～1.5 MPa。

图8表明：本文中计算方法得到的结果与经验公式得到的结果有很大范围的重合区域，证明本文中计算临界震塌厚度的方法是合理的。本文中推导的计算参数是经验系数的科学解释，揭示了其内在的物理本质，式(55)的适用范围更广、考虑的关键参数更全面。

5 结 论

将介质表面接触爆炸问题转换初始冲击体撞击周围介质的问题，利用极值原理，推得爆炸抗力，结合初始条件及边界条件求解运动方程，得到了临界震塌厚度和临界贯穿厚度，通过算例分析得到以下结论：(1)临界厚度由量纲一冲击因子ξ决定，它们大致呈正比关系。ξ反映了炸药能量效率和介质强度的影响特性，它代表着炸药对介质的爆破能力。炸药爆热、密度、比能量系数越大，说明炸药的爆破效率越高，算得的ξ越小，临界厚度越大；介质屈服强度越高，说明其可爆性越差，介质对炸药的抵抗能力越强，算得的ξ越小，临界厚度越小。(2)定量描述了临界厚度与ξ的关系；可以看到同一ξ下，临界震塌厚度约为临界贯穿厚度的2倍，这与BRL公式、修正BRL公式一致。(3)通过与经验公式对比分析，证明本文中计算方法是合理的。理论推导所得的计算公式揭示了经验公式的物理本质。

[1] 郑全平,钱七虎,周早生,等.钢筋混凝土震塌厚度计算公式对比研究[J].工程力学,2003,20(3):47-53. Zheng Quanping, Qian Qihu, Zhou Zaosheng, et al. Comparative analysis of scabbing thickness estimation of reinforced concrete structures[J]. Engineering Mechanics, 2003,20(3):47-53.

[2] 张想柏,杨秀敏,陈肇元,等.接触爆炸钢筋混凝土板的震塌效应[J].清华大学学报:自然科学版,2006,46(6):765-768. Zhang Xiangbai, Yang Xiumin, Chen Zhaoyuan, et al. Explosion spalling of reinforced concrete slabs with contact detonations[J]. Journal of Tsinghua University: Science & Technology, 2006,46(6):765-768.

[3] 郑全平,周早生,钱七虎,等.防护结构中的震塌问题[J].岩石力学与工程学报,2003,22(8):1393-1398. Zheng Quanping, Zhou Zaosheng, Qian Qihu, et al. Spallation in protective structures[J]. Chinese Journal of Rock Mechanics and Engineering, 2003,22(8):1393-1398.

[4] Haldar A. Penetration depth in concrete for nondeformable missiles[J]. Nuclear Engineering and Design, 1982,71(1):79-88.

[5] Hughes G. Hard missile impact on reinforced concrete[J]. Nuclear Engineering and Design, 1984, 77(1):23-35.

[6] 王明洋,邓宏见,钱七虎.岩石中侵彻与爆炸作用的近区问题研究[J].岩石力学与工程学报,2005,24(16):2859-2864. Wang Mingyang, Deng Hongjian, Qian Qihu. Study on problems of near cavity of penetration and explosion in rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2005,24(16):2859-2864.

[7] 王明洋,钱七虎,赵跃堂.接触爆炸作用下钢板-钢纤维钢筋混凝土遮弹层设计方法(II)[J].爆炸与冲击,2002,22(2):163-168. Wang Mingyang, Qian Qihu, Zhao Yuetang. The design method for shelter plate of steel plate and steel fiber reinforced concrete under contact detonation (II)[J]. Explosion and Shock Waves, 2002,22(2):163-168.

[8] 王德荣,戴明,李杰,等.钢纤维超高强活性混凝土(RPC)遮弹板接触爆炸破坏作用[J].爆炸与冲击,2008,28(1):67-74. Wang Derong, Dai Ming, Li Jie, et al. Failure effect of steel-fiber reactive power concrete (RPC) shelter plate under contact explosion[J]. Explosion and Shock Waves, 2008,28(1):67-74.

[9] 王德荣,宋华,赵跃堂,等.钢纤维超高强活性混凝土(RPC)遮弹板接触爆炸局部破坏实验研究[J].爆破,2006,23(3):5-9. Wang Derong, Song Hua, Zhao Yuetang, et al. Expermental investigation of local failure of steel-fiber reactive power concrete (RPC) shelter plate under contact explosion[J]. Blasting, 2006,23(3):5-9.

[10] 李业学,谢和平,彭琪,等.活性粉末混凝土力学性能及基本构件设计理论研究进展[J].力学进展,2011,41(1):51-59. Li Yexue, Xie Heping, Peng Qi, et al. Progress in mechanic property and design theory of elementary struture of reactive powder concrete (RPC)[J]. Advanced in Mechanics, 2011, 41(1): 51-59.

[11] 葛涛,刘宝荣,王明洋.弹体侵彻与贯穿有限厚度混凝土靶体的力学特性[J].爆炸与冲击,2010,30(2):159-164. Ge Tao, Liu Baorong, Wang Mingyang. Perforation of concrete targets with finite thickness by projectiles deceleration[J]. Explosion and Shock Waves, 2010,30(2):159-164.

[12] 宋春明,王明洋.混凝土板受刚性弹撞击的贯穿系数研究[J].震动与冲击,2008,27(11):101-104. Song Chunming, Wang Mingyang. Study on perforation coefficient of concrete plate impacted by rigid projectiles[J]. Journal of Vibration and Shcok, 2008,27(11):101-104.

[13] 王明洋,施翠英,陈士林.事故型撞击混凝土板的临界震塌与贯穿厚度计算方法[J].工程力学,2009,26(11):238-246. Wang Mingyang, Shi Cuiying, Chen Shilin. Method of calculating critical spalling and penetration thickness of concrete slab of block under accident impact[J]. Engineerging of Mechanics, 2009,26(11):238-246.

[14] 王明洋,张胜民,国胜兵.接触爆炸作用下钢板-钢纤维钢筋混凝土遮弹层设计方法(Ⅰ)[J].爆炸与冲击,2002,22(1):40-45. Wang Mingyang, Zhang Shengmin, Guo Shengbing. Design method of steel and steel-fiber concrete shelter plate under contact detonation(I)[J]. Explosion and Shock Waves, 2002,22(1):40-45.

[15] 李晓军,郑全平,杨益.钢纤维钢筋混凝土板爆炸局部破坏效应[J].爆炸与冲击,2009,29(4):385-389. Li Xiaojun, Zheng Quanping, Yang Yi. Local damage effects of steel fiber reinforced concrete plates subjected to contact explosion[J]. Explosion and Shock Waves, 2009,29(4):385-389.

[16] Kachanov L M.Plasticity theory foundation[M].North-Holland Amsterdam: Dover Publications, 1971.

[17] 陈灿寿,施翠英,王明洋.锥形弹低速冲击混凝土板的震塌与贯穿效应研究[C]∥全国工程安全与防护学术会议论文集,2008.

[18] 施翠英,王明洋.平头弹低速冲击混凝土板的震塌与贯穿效应研究[C]∥全国工程安全与防护学术会议论文集,2008.

[19] 王明洋,陈士林,潘越峰.平头弹在岩石(混凝土)介质中的侵彻计算方法[J].兵工学报,2005,26(1):46-52. Wang Mingyang, Chen Shilin, Pan Yuefeng. Method of calculation for the penetration of a flat-nosed projectile in the rock (concrete)[J]. Acta Armamentarii, 2005,26(1):46-52.

[20] Henrych J. The dynamics of explosion and its use[M]. Holland: Elsevier Scientific Publishing Company, 1979.

[21] Hill R. The mathematical theory of plasticity[M].Oxford, UK: Oxford University Press, 1950.

[22] 文鹤鸣.混凝土靶板冲击响应的经验公式[J].爆炸与冲击,2003,23(3):267-277. Wen Heming. Empirical equations for the impact response of concrete targets[J]. Explosion and Shock Waves, 2003,23(3):267-277.

(责任编辑 王小飞)

A method for calculating critical spalling and perforating thicknesses of concrete slabs subjected to contact explosion

Yue Songlin, Wang Mingyang, Zhang Ning, Qiu Yanyu, Wang Derong

(StateKeyLaboratoryforDisasterPrevention&MitigationofExplosion&Impact,PLAUniversityofScienceandTechnology,Nanjing210007,Jiangsu,China)

Tanking account of the mass conservation conditions, incompressible conditions and boundary conditions, this paper described the dynamic behaviors of the medium based on the plastic-rigid model and established the compatible dynamic velocity field in the plastic zone. In addition, utilizing the limit equilibrium theory, this paper derived the equations of material resistance to explosions in both the infinite and the semi-infinite medium. Combined with the initial and boundary conditions, the equations of motion can be solved and the critical depth can be obtained. Besides, this paper has obtained a dimensionless impact factor which reflects the integrated nature of explosive sources and media. The calculated results illustrated that the critical depth and the dimensionless impact factor have a proportional relationship. Finally, the comparative analysis of the empirical formulas with the derived equations proved that our calculation methods are valid and widely applicable.

mechanics of explosion; critical thickness; plastic-rigid model; the limit load theorems; contact explosion; spallation; perforation; dimensionless impact factor

10.11883/1001-1455(2016)04-0472-11

2013-09-18；

2014-12-21

国家自然科学青年基金项目(51308543)；教育部长江学者和创新团队发展计划项目(IRT13071)

岳松林(1987- )，男，博士研究生；

王明洋，wmyrf@163.com。

O381国标学科代码：13035

A