用地震数据估算填方残留层物性参数的数值试验

韩 超，付小波，原健龙，钱 广，余嘉顺

(成都理工大学地球物理学院，成都 610059)

用地震数据估算填方残留层物性参数的数值试验

韩 超，付小波，原健龙，钱 广，余嘉顺

(成都理工大学地球物理学院，成都 610059)

为确定某海滩工程填方场址下伏残留层介质的厚度、密度、地震横波速度以及品质因子等物性参数，提出以地震观测数据为约束，通过模拟场址地震响应来估算残留层介质参数的方法。介绍了该方法的原理以及算法过程，给出了数值试验示例。结果表明，除了填方残留层介质的品质因子对地震数据影响显著性较低而较难精确确定之外，用该方法确定的残留层层厚、密度、横波速度等介质参数与验证模型吻合程度很高，说明了该方法具可行性。

填方工程;地层物性参数;模拟估算;地震动响应

某海滩填方工程下有大量淤泥，因淤泥清除或者固化成本较高，环境保护需要保留这些海相沉泥，故选择不对淤泥层进行处理直接填土覆盖，因此形成了一个存在下伏软弱夹层的工程场址基础结构(图1)。有研究表明，场址下伏软弱夹层会在地表形成地震共振放大效应［1－2］，因此，后期的地面建筑工程设计需要了解填方之后软弱夹层的物性参数，以便作出相应的设计对策。当年填方作业之前，工程施工方按照业主要求对海滩淤泥层及下部基岩进行过勘探，并对其物性参数作过测定。但是工程填方完成之后，由于上覆岩土的压实作用，淤泥层的厚度以及物性参数都发生了变化，上述勘探测定的数据无法直接采用，需要重新进行测定。要取得这些参数信息，钻探无疑是最直接有效的方法，通过测井数据可以准确获得指定位置的地层参数。但是为此而进行大规模、大面积的钻探施工，费用成本过高，业主希望另外寻找性价比较好的解决办法。

考虑到该工程场址位于地震活动较为频繁的地区，容易接收记录到天然地震波数据，而且在施工前该海滩已有地质勘探资料，可以为填方之后的场址模型提供一定的参数估计基础。因此，结合天然地震资料进行参数反演是一个成本较低的选择。

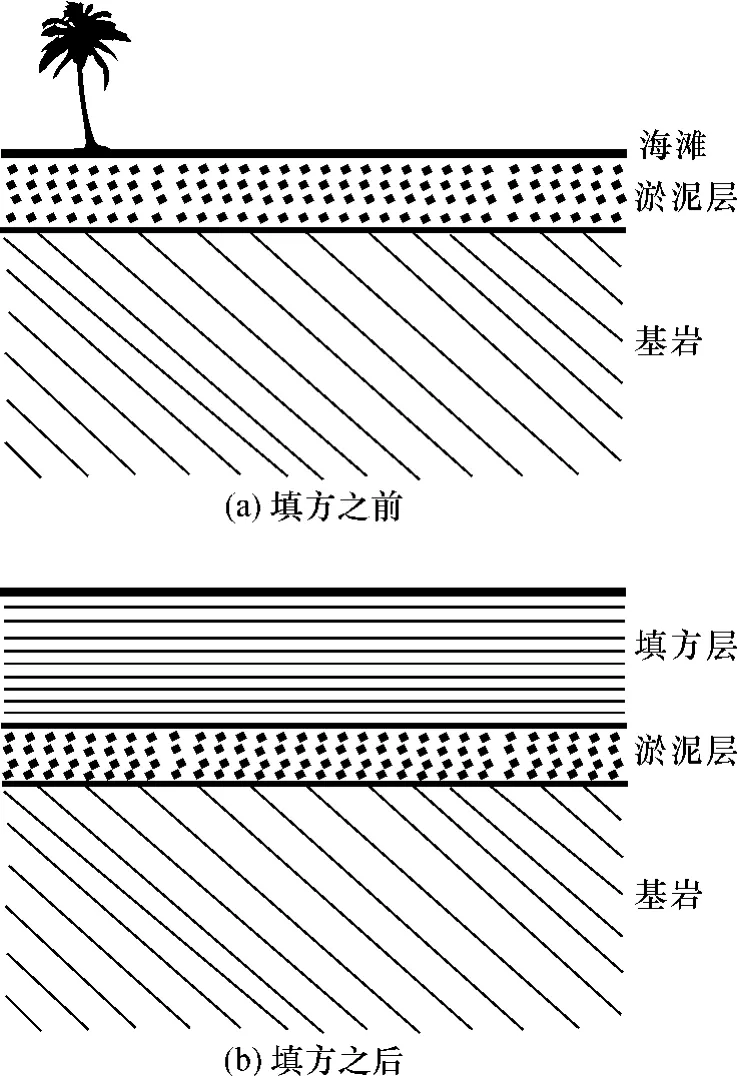
图1 海滩工程场址填方前后结构示意图Fig.1 Beach site structure before and after reclamation engineering

通过工程物探数据的反演，也能得到地层相关土质参数。例如，利用地震勘探数据能反演出地层介质的分层埋深情况［3］，但是用反射勘探法成本偏高，而折射波勘探方法则存在下伏软弱夹层速度倒转的限制。采用基于测井数据的目标函数约束反演［4－5］，可以获得介质的波阻抗参数信息，但是同样需要测井资料。此外，也有用振幅法［6］、上升时间法［7］或衰减成像质心频率偏移法［8］等来反演地层介质的品质因子的成功尝试。振幅法需要测定稳定的真振幅，在现实中实现难度较大;上升时间法对噪音干扰非常敏感［9］;而质心频率偏移法精度较低。

为此，考虑利用原先的勘探资料以及工程填方提供的资料，给定一个具体参数待定的初始场址模型，以地震资料为约束，进行关于场址地震响应的模拟计算比较分析，最终达到对场址模型中软弱夹层的分层参数以及物性参数进行确定性估算的目的。

1 方法原理

一个场址的地表地震动响应与该场址下方的地质结构有关［10］。所谓场址的地表地震动响应，是由研究场址地震记录的傅里叶振幅谱与参考场址地震记录的傅里叶振幅谱的谱比函数［11］来刻画的。对于一个确定的场址结构，其地表地震动响应特征是一定的。为此，在已知场址结构模型的情况下，可以通过计算机模拟，计算得到对该场址地震响应的估计。如果场址模型对场址地下地质结构的刻画比较精确，采用的模拟计算方法精度较高，那么，模拟计算得到的响应函数与在该场址上接受天然地震得到的地震动响应特征可以有比较好的吻合度［12］。基于该原理，可以在该场址进行24 h连续地震观测，根据国家地震台网的地震目录参数，设定合适的地震事件持续振动时间窗口提取地震数据［13］，再采取传统的谱比法计算得到观测场址的地震动响应［14］。然后，通过建立足够大量的各种场址模型，使得其中存在一个或多个模型与真实的场址地质结构近似。那么，逐一对这些模型进行模拟计算，并将计算得到的响应特征函数与实际观测得到的场址地震动响应函数进行对比，选择出吻合最好的模拟函数所对应的模型作为对该场址地下地质结构的估计，进而得到所关心的软弱夹层的介质参数情况。研究流程如图2所示。

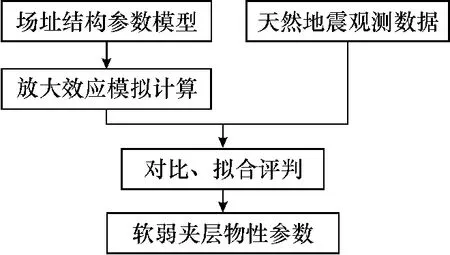
图2 解决思路框图Fig.2 Flow chart of the solution

上述解决方法实际上是一个反演过程。反问题是可能存在多解性的，也就是说，一个场址结构所对应的地表地震动响应函数是唯一确定的，但是一个地表地震动响应函数所对应的地下地质结构却不一定是唯一的。在不存在多解性的情况下，只要寻找到吻合度高的响应函数，就可以确定其所对应的地下地质模型。而在存在多解性的情况下，上述解决方法则不一定是可行的。对于这个场址的结构类型而言，上述方法是否可行，首先需要排除多解性的难题。在开展实际观测之前，先合成一个数值模型的响应函数来代表观测的响应函数，在数值上开展模拟试验，考察该工程场址地质结构类型的多解性情况。

不同的地震仪器记录到的地震数据类型是不同的。工程勘察采用的弱震记录仪器记录到的通常是振动速度数据。由于本方法所用的“谱比”概念本身是一个无量纲的量，记录仪器响应对其没有影响。因此，只要仪器的一致性得到满足，本方法在原理上既可用于速度记录数据，也适用于位移记录数据或者加速度记录数据。

2 场址结构模型

该工程场址的地质结构在宏观上可以用一个3层模型来表述 (图3)，从地表向下依次为填方形成的地表盖层、原先海滩淤泥在填埋之后形成的软弱夹层以及最下面的下伏基岩。

上覆盖层为填方形成，层内介质从上至下受到的压力逐渐增大，介质的重力夯实效应可致使介质密度、地震波速度以及品质因子Q随深度而增大。尽管不知道该介质的确切参数值，但了解其随深度而增大的随机变化特点，因此可以用一个指数函数来描述这些参数随深度的变化规律

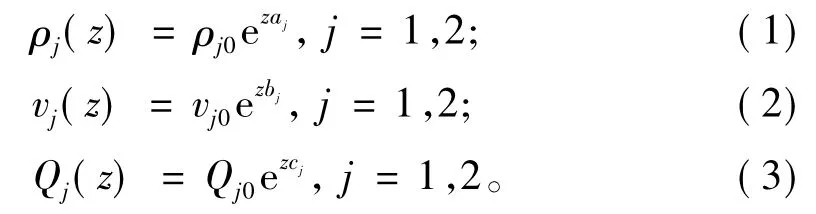
式中:ρj(z)、vj(z)和Qj(z)分别为介质的密度、波速以及品质因子随深度z的变化函数，其中j=1，2分别表示上覆盖层和软弱夹层;ρj0、vj0和Qj0分别是第j层顶界面的密度、横波速度和品质因子;aj、bj和cj分别是密度、横波速度和品质因子的变化系数。

相对于盖层与淤泥软弱夹层，填方过程对底部基岩层的介质参数影响不大，因此场址模型中的底部基岩层的物性参数，包括介质密度ρ、横波速度v和品质因子Q等介质参数信息，均可以直接根据填方之前的勘探数据来确定。

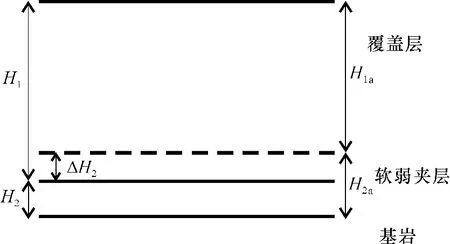
图3 场址软弱夹层经受夯实作用后的厚度变化示意图Fig.3 Thickness variation of the buried weak layer due to tamping effect

将上覆盖层和软弱夹层的厚度分别记为H1和H2。因不能准确知道这两个厚度参数，但是可知道填方之前的软弱夹层厚度，记为H2a(图3)。按照业主要求，填土层的顶界面高程位置在原始海滩顶界面上方H1a高度处。在填方施工之后，由于压实作用，软弱夹层的原始厚度会减少ΔH2，其顶界面埋深位置由虚线所示之处下降到箭头所指实线处，其厚度变为H2;在海滩层厚被压缩的同时，填土层的厚度变为H1。这些地层厚度参数的关系可表示为

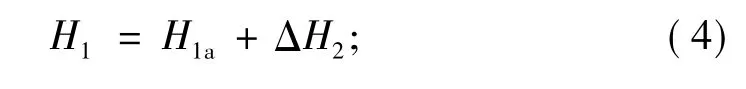
在上述模型参数中，盖层与软弱夹层的厚度H1a和H2a为已知;介质在地面的参数ρ10、v10和Q10值可以直接在地面进行测定;而模型底部基岩层的物性参数ρ、v和Q亦可由填方之前的勘探数据提供。因此，模型的未知参数包括夹层厚度压缩值ΔH2，夹层顶板介质参数值ρ20、v20和Q20，盖层和夹层的变化系数aj、bj和cj，其中j=1，2。

事实上，由于该工程场址的夹层厚度不大，夹层内部介质参数的相对变化对场址地面地震动响应不会造成显著影响，因此，可以将夹层介质参数近似看作是均匀的，即a2=b2=c2≡0。在此假设条件下，未知的模型参数减少为7个，即ΔH2、a1、b1、c1、ρ20、v20和Q20。

3 模拟试验

3.1 验证模型

为验证上述方法的可行性，需要合成一个该海滩的场址模型作为验证的目标。根据施工数据、施工前勘探数据以及施工后在场址地表测定的数据，场址的有关参数见表1。

表1 场址地下结构参数Table 1 Underground structure parameters of the site

考虑到填方层和软弱夹层的层内介质并不是理想均匀的，验证模型的地层结构物性参数应该具有一定随机变化特点。为此，采用N个不连续的随机薄层来刻画盖层。只要N足够大，就可以较精细地反映出模型盖层内介质随深度随机变化的特征［15］。

为了构筑一套随机分层系列，这里引入Box-Muller随机函数［16］

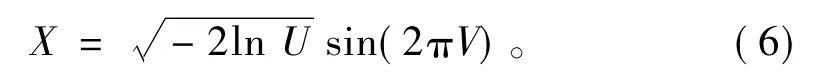
其中，X由两组独立的均匀分布随机数U和V生成，满足标准正态分布规律，其概率密度函数见图4。

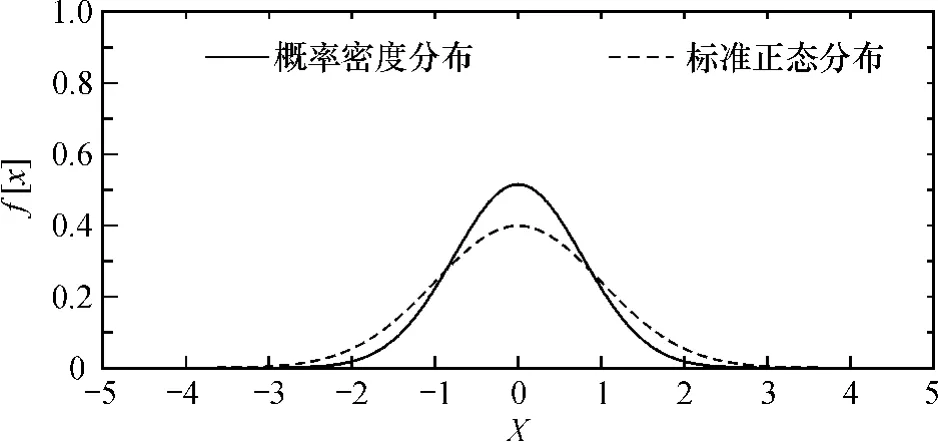
图4 场址结构分层参数所满足的概率密度分布模型Fig.4 Probability density distribution model satisfied by layered parameters of site structure

利用这个随机数，定义验证模型的参数

其中:j=1，2分别表示盖层和软弱夹层;hji、zji、ρji、vji和Qji分别表示第j层地质体内的第i分层的厚度、顶界面埋深、介质密度、横波速度和品质因子;αj、βj、γj和ηj分别各分层厚度、横波速度、密度、品质因子随机变化程度的控制系数;Xji为各分层的随机数。特别地，

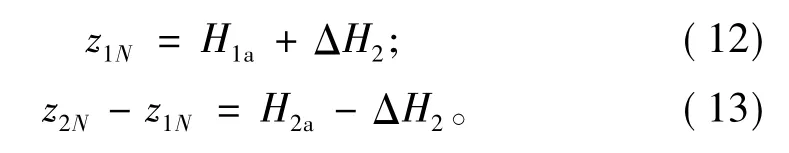
上述各式中的具体参数值由表2给定，模型结构的参数值均在表1的相应参数范围之内。

由式(7)～(13)以及表2中的参数值所确定的验证模型如图5所示。3.2 模拟计算

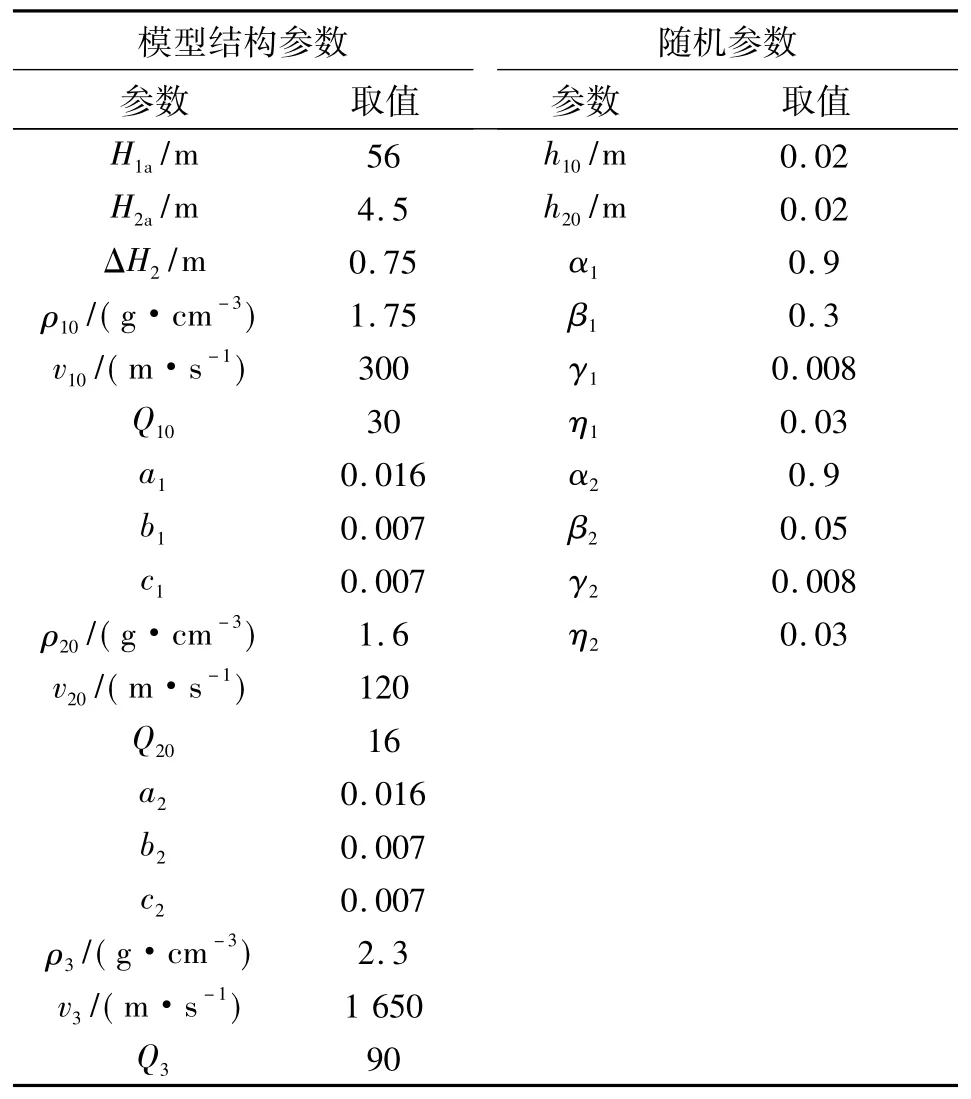
表2 验证模型的参数取值Table 2 Parameters of the verificationmodel

图5 验证模型Fig.5 Verificationmodel

根据对场址结构的认识(表1)，有7个未知参数待定。取ΔH2的分辨率为0.225 m;a1、b1、c1的分辨率分别为0.000 5、0.004、0.001;ρ20、v20的分辨率分别为0.1 g/cm3和20 m/s，并设软弱夹层内部介质变化可用均匀层来近似，即a2=b2=c2= 0。那么，可能的离散参数模型将由表3的参数组合完全给定。模型个数为

对一般工程问题来说，SH波在地表的响应特征可以较好地刻画场址表层地震动响应函数［17－19］。本文采用一种可以用细薄层无限逼近连续变化介质模型的SH波响应的模拟方法［20］来进行模拟计算。地震震源深度通常远远大于工程填方层的底界面深度，震源所在位置的介质地震波速度也通常远远大于填方层的底界面介质地震波速度，根据Snell定理，在这种情况下地震波以接近垂直方向入射到填方层。在上述模型参数精度条件下，12 096个模型中至少存在一个模型与验证模型的吻合满足精度要求。考虑到现有计算能力完全可以胜任对12 096个模型的正演模拟，所以直接通过对这12 096个模型进行通盘模拟比对，从中找出验证模型的近似解。

表3 场址模型的参数取值Table 3 Parameters of the sitemodel

对每个模型作SH波振幅地表响应正演数值模拟的时候，以0.1 Hz的间距计算0.1～20 Hz共200个频率的振幅谱比，包括1个验证模型的响应函数和12 096个场址模型的响应函数。

模拟结果表明，地下介质的分层、密度、横波速度及品质因子等参数的变化差异对SH波振幅地表响应有显著的影响。图6列举了4个模型及其响应函数。其中模型A和D的响应函数差异很大，从因果关系看，模型A和D的参数差异很大，其中盖层和软弱夹层的速度、密度、品质因子都存在显著的差异。再对比模型A和B，两者响应特征很相似，从它们的模型结构参数对比中发现，两者的物性参数很相近。模型C与A的参数相似度介于B和D之间，对应的地震响应特征的相似度同样介于B、D分别与A的相似度之间。这说明，场址地震动响应特征与场址结构的特征关系紧密，场址的响应函数在一定程度上能够体现它的物性参数结构差异。

有研究表明［21］，低频段的SH波振幅放大效应对地表结构、建筑的稳定性影响最显著。初步模拟研究发现，该场址结构模型的地震响应主频主要位于几到十几赫兹的频段范围之内，为此，主要对20 Hz以内的放大效应作分析，了解各个模型的响应函数特征与验证模型的响应函数特征之间的相似度或差异程度。

3.3 目标函数

在判断两个响应函数的相似程度或差异程度的时候，可以考虑的响应函数的特征有:放大效应波峰的个数、放大波峰的幅值大小与频率位置以及响应函数的整体变化趋势，包括波峰的频率宽度范围、响应数值随频率的衰减规律等。为此，采用以下函数来刻画场址模型与验证模型响应函数之间的误差

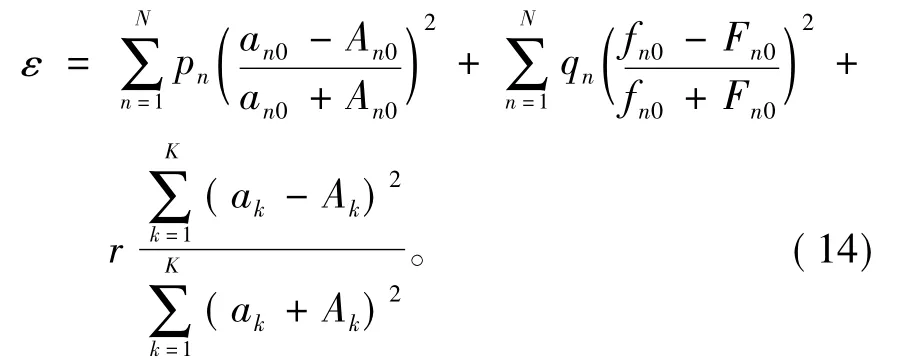
其中:右边第1项为振幅峰值的误差，an0为场址模型响应函数a(f)的第n个振幅峰值，An0为验证模型响应函数A(f)的第n个振幅峰值;第2项为振幅峰值的频率差，fn0和Fn0分别为场址模型和验证模型响应函数的第n个振幅峰值对应的主频;第3项为响应曲线整体振幅的差，ak和Ak分别为场址模型和验证模型响应函数的第k个离散振幅值。an0、An0、fn0及Fn0由下式确定

其中，a(f)与A(f)为相应地下介质模型的SH波响应函数，由地下介质的密度函数ρ(z)、横波速度函数vs(z)与品质因子函数Q(z)有关。在形式上可表达为

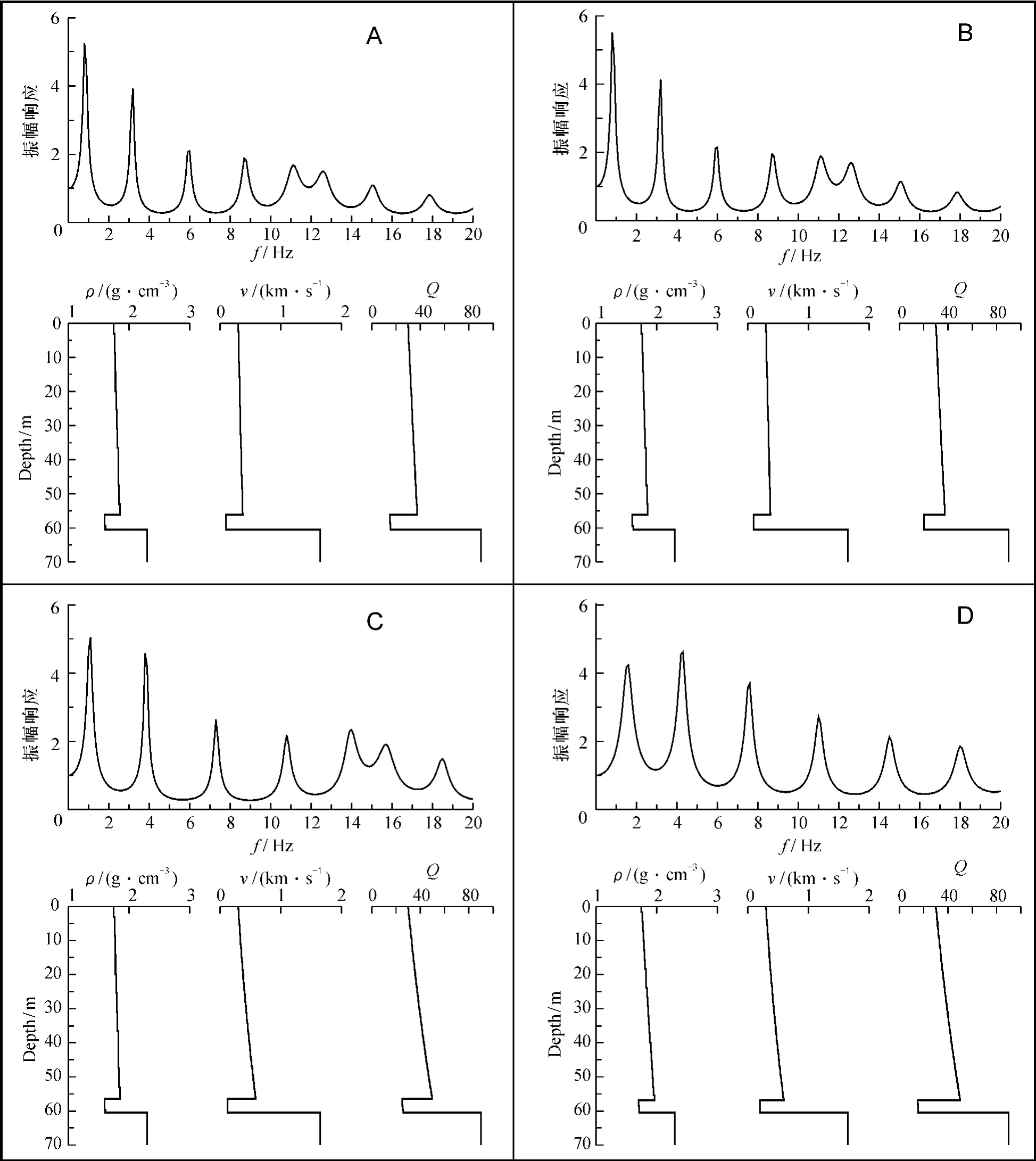
图6 场址模型及其SH波振幅地表响应结果示意图Fig.6 Sitemodels and SH-waves amplitude responses A、B、C和D分别表示4种不同的模型结构

a(f)=g［ρ(z)，vs(z)，Q(z)］， (17)

其中的函数算子g［·］不具简单的显式表达，须由一组比较复杂的方程组通过递推实现。其具体表达式及计算方法可参见文献［20］。其中离散间隔为0.1 Hz，这3项误差权系数p、q、r满足如下关系

在试验中重点考察前面5个波峰的相似程度，即取N=5。经过反复数值试验，对目标函数的参数设置如表4所示。

上述定义的目标函数取值范围为ε∈［0，1］，ε越小表明响应函数与目标越接近。

在数值试验过程中发现，目标函数各项的权系数对拟合结果有很重要的影响。其中，p对阻抗比变化很敏感，q对模型层厚与横波速度的比变化很敏感，而r则可较好地控制模型物性参数结构特征的整体差异。

表4 误差估计函数的参数取值Table 4 Parameters of the error estimation function

4 结果分析

将12 096个场址模型与验证模型的响应函数逐一对比，通过上述目标函数对它们的相似度作评判，由此得出目标函数值最小(0.001 425)的响应函数，从而筛选出其对应的场址模型。结果显示，这样的筛选方式得到的场址模型与验证模型的响应函数、参数结构的吻合度都很好(图7)，表明以最佳拟合的场址模型可以较好刻画验证模型的结构参数特征。也就是说，可以用这个方法估算出软弱夹层的介质参数。

从统计意义上说，一个成功例子是有可能存在偶然因素的。为了消除这种可能性，笔者决定进行更多的验证比较试验。为此，用与上述例子相同的方式合成了50个各不相同而且相互独立的随机验证模型。对每个验证模型都分别进行一套与上述过程相同的模拟，根据其最小目标函数原则得到一个最佳估计模型，总共得到了50个最佳拟合场址模型。把这50个场址模型的软弱夹层压缩厚度、密度、横波速度和品质因子的数值分布作统计，结果如图8所示。

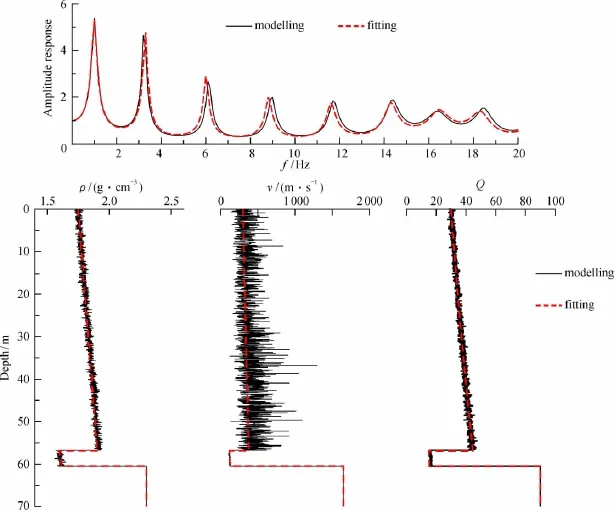
图7 验证模型与最佳拟合场址模型的响应函数、结构参数的对比Fig.7 Comparison of the amplitude response and parameters of structure between the verification model and the best fittingmodel of the site

图8 50次最佳拟合模型软弱夹层的压缩厚度、密度、横波速度和品质因子统计分布Fig.8 Statistics of compression thickness，density，seismic shear wave velocity and quality factors for the imbedded softweak layer in the 50 best fittingmodels

验证模型的软弱夹层ΔH2、ρ20、v20和Q20分别为0.75 m、1.6 g/cm3、120 m/s和16。从图8可以看出，拟合得出的软弱夹层压缩厚度有42组在0.675 m，其余的8组在0.900 m，与验证模型的压缩厚度0.75 m吻合度很高;0.675 m与验证模型的压缩厚度0.75 m最为接近，以此为标准，准确率占了84%。密度大部分是准确的，50组密度数据中有46组是1.6 g/cm3，概率达到了92%。横波速度是完全吻合的，均为120 m/s，准确率100%。对品质因子的估计主要集中在20，与验证模型的品质因子数值16相比较，整体稍微偏大。

数值试验的结果表明，本方法能够确定地下结构模型的物性参数，对于软弱夹层的层厚、介质密度和横波速度，估算结果精度较高。由于品质因子对模型地表响应函数的影响并不太明显，因此在确定此参数时，估算结果存在一定的误差。另外，上述目标函数主要考虑了振幅响应函数12 Hz以内频段范围的部分，而品质因子对地震波的低频部分影响较弱，所以品质因子的估算敏感度较低。

试验还发现，随着βj、γj和ηj的取值范围变大，即横波速度、密度和品质因子随机变化范围变大，用上述搜索方法估算软弱夹层介质参数的难度会随之增大，最终得到的估算参数的精度也会明显下降。

为了解本文的数值试验方法在噪音干扰条件下的适用性，还对模型的场址响应函数加入不同程度的噪音，用第3节的计算方法估算残留层物性参数并进行统计对比分析。为了加入真实的地震观测数据中的背景噪音，这里使用2013年4月25—27日在四川省芦山县城区观测的地震数据来计算背景噪音。地震监测台站在50 h内观测到280个地震事件，以P波到时前10 s和S波到时后10 s分别作为噪音背景信号和地震动信号［22］，计算每个地震事件的信噪比，分析信噪比结果，以其中观测记录质量较好的50组地震动数据的信噪比均值作为背景噪音(图9)。

结果显示，背景噪音为地震动信号的2.5%，并且有随着频率的增高而变大的轻微趋势。

图9 背景噪音统计结果Fig.9 Statistics of background noise

为了应对地震观测数据质量并非足够理想的情况，将背景噪音放大至5%和10%，讨论不同程度噪音背景干扰情况下数值试验对残留层物性参数的估算结果。从图10看出，背景噪音对残留层密度ρ20的估算无显著影响;品质因子本身就是估算敏感度较低的物性参数，因此加入背景噪音后对残留层Q20的估算结果仍然在合理范围。这里主要考察不同程度背景噪音下，数值试验对残留层压缩厚度 ΔH2和横波速度 v20的估算结果: 2.5%背景噪音对残留层物性参数估算结果的影响较小(图10b)，与无背景噪音的试验结果很相似; 5%背景噪音下，ΔH2的估算结果与无背景噪音情况下相比，开始出现一定程度的偏差(图10c)，但估算结果的整体趋势仍然是围绕于目标参数值;当背景噪音达到10%，估算的残留层的ΔH2和v20与无背景噪音情况下的估算结果之间差别较大(图10d)。因此，在采用实际地震数据进行场址参数估计的时候，数据质量是至关重要的，必须选取质量好的数据作分析，才能取得满意的估算精度。

图10 不同噪音背景情况下的残留层物性参数估算统计结果Fig.10 Statistics of estimated medium parameters on different noise levels

分层分辨率在很大程度上取决于数据的频谱特性，尽可能采用含有丰富高频成分，而且信噪比较高的数据，是保证参数估计精度和分层分辨率的重要条件。为了探讨本文数值试验的可行性，还需要了解实际观测到的地震动频谱是否可以提供足够的频率信息。上述数值试验主要分析0.1～20 Hz频率范围的场址响应函数，并且在计算目标函数时重点考察的数据段频宽范围在0.1～12 Hz。地震动频谱能量的分布特征与震中距、震级等因素相关，通常，近震中距比远震中距的地震动高频能量多，小地震比大地震的地震动高频能量多。因此这里列举一个实际观测的震级较小、震中距较近的地震事件，结合数值试验方法讨论分析频谱的能量分布情况(图11)。该事件的地震目录为——发震时刻:2013年4月25日16时07分00秒;震中坐标:30.24°N，102.84°E;参考位置:四川省宝兴县;震源深度:12 km;震中距: 13 km;震级大小:2.8 ML。图11a是经过仪器响应函数校正之后得到的速度记录，图11b是对应的傅里叶振幅谱，其能量主要集中在20 Hz以内，特别在15 Hz内显示出较强的振动能量，其中水平分量NS和EW相对垂直分量UD更为显著。以此为例，这种震中距较近、震级较小的地震动包含丰富的高频信息，其频谱特征适用于本文的数值试验方法。同样，由于在地震活动频繁的地带能够较为容易观测到震中距近的小震级地震事件，这为数值试验的合理性和可行性提供了必要基础。

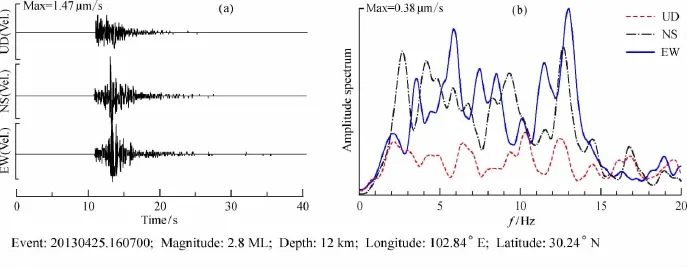
图11 某一地震事件三分量地震动波形时间记录(a)和对应振幅谱(b)Fig.11 Seismic time records of three components(a)andamplitude spectrum(b)in an earthquake event

5 结论

通过数值试验发现，本文提出的方法能够较为精确估算海滩场址软弱夹层的层厚、密度、横波速度、品质因子等参数。其中，分层厚度和横波速度对地表响应函数的影响最为突出，因此误差估计函数对这两种参数最为敏感，这两种参数的估算精度较高。因为地表地震响应对地下介质密度变化的敏感性稍弱，所以有少数密度估算值存在轻微偏高的情况。由于品质因子对振幅地表响应的低频成分影响不大，所以品质因子估算的灵敏度没有其他参数那么高。方法原理设想中提到的参数反演多解性问题，在本研究中没有对数值试验结果造成显著影响。数值试验的统计结果表明，本文所采用的模拟估算方法是可行的，能够确定填方施工之后海滩软弱夹层结构的物性参数。

最后必须指出，在模型数量规模不大的情况下对所有的模型全局逐一搜索拟合方案是可行的。但是，如果模型参数范围变大，参数采样精度变高，模型数量会变得非常大，实现全局搜索的工作量将会变得难以承受。为此，笔者计划引进优化反演算法，对本方法的适用范围作进一步扩展。

［1］黄润秋，余嘉顺．软弱夹层的地震动强度效应研究［J］．自然科学进展，2003，13(11):1177－1181．

［2］黄润秋，余嘉顺．软弱夹层特性对地震波强度影响的模拟研究［J］．工程地质学报，2003，11(3):312－317．

［3］李录明，李正文．地震勘探原理、方法和解释［M］．北京:地质出版社，2005:17－24．

［4］张宏兵，杨长春，尚作萍，等．基于软约束模式的波阻抗反演［J］．地球物理学进展，2006，21(3):837－844．

［5］朱成宏．地震资料波阻抗多尺度反演［J］．石油物探，1999，38(2):20－30．

［6］Zhang ZM，Stewart R R，Lawton D C．Estimating seismic attenuation(Qp＆Qs)from rock properties［J］．Canadian Journal of Exploration Geophyslcs，2013，38(1):1－3．

［7］Gladwin M T，Stacey F D．Anelastic degradation of acoustic pulses in rock［J］．Physics of the Earth and Planetary Interiors，1974，8(4):332－336．

［8］Quan Y L，Harris JM．Seismic attenuation tomography using the frequency shift method［J］．Geophysics，1997，62 (3):895－905．

［9］Blair D P，Spathis A T．Attenuation of explosion-generatedpulse in rock masses［J］．Journal of Geophysical Research，1982，87(B5):3885－3892．

［10］Hainse A J，Yu J．Observation and synthesis of spatially-incoherent weak-motion wavefields at Alfredton basin，New Zealand［J］．Bulletin of the New Zealand National Society for Earthquake Engineering，1997，30(1):14－31．

［11］Steidl JH，Tumarkin A G，Archuleta R J．What is a reference site? ［J］．Bulletin of the Seismological Society of A-merica，1996，86(6):1733－1748．

［12］Semblat JF，Duval AM，Dangla P．Seismic site effects in a deep alluvial basin:Numerical analysis by the boundary element method［J］．Computers and Geotechnics，2002，29 (7):573－585．

［13］梁群．玉皇观河口区域表层地震放大效应研究［D］．成都:成都理工大学，2014．

［14］章立波，谢礼立，郭明珠．利用强震记录分析场地的地震反应［J］．地震学报，2001，23(6):604－614．

［15］余嘉顺，贺振华．一种模拟随机数字地层模型的方法［J］．地震研究，2004，27(4):344－349．

［16］Box G E P，Muller M E．A note on the generation of random normal deviates［J］．The Annals of Mathematical Statistics，1958，29(2):610－611．

［17］Olsen K B．Site amplification in the Los Angeles basin from three-dimensionalmodeling ofgroundmotion［J］．Bulletin of the Seismological Society of America，2000，90(6B):S77－S94．

［18］Lee S J，Chen H W，Huang B S．Simulations of strong ground motion and 3D amplification effect in the Taipeibasin by using a composite grid finite-differencemethod［J］．Bulletin of the Seismological Society of America，2008，98 (3):1229－1242．

［19］Adams BM．Basin-edge effects from SH-wavemodelling with reference to the Lower Hutt Valley，New Zealand［D］．New Zealand:University of Canterbury Christchurch，2000．

［20］余嘉顺，贺振华．SH波在表面多层介质中传播的精确模拟［J］．地震研究，2003，26(1):14－19．

［21］Yu JS，Haines J．The choice of reference sites for seismic ground amplification analyses:Case study at Parkway，New Zealand［J］．Bulletin of the Seismological Society of America，2003，93(2):713－723．

［22］Strollo A，Richwalski SM，Parolai S，et al．Site effects of the 2002 Molise earthquake，Italy:Analysis of strongmotion，ambient noise，and synthetic data from 2D modelling in San Giuliano di Puglia［J］．Bulletin of Earthquake Engineering，2007，5(3):347－362．

Numerical experiment of determ ination ofmedium parameters for reclamation engineering layers by seism ic data

HAN Chao，FU Xiao-bo，YUAN Jian-long，QIAN Guang，YU Jia-shun
(College of Geophysics，Chengdu University of Technology，Chengdu 610059，China)

To determine the depth，density，seismic velocity and quality factor values of a buried soft layer resulting from reclamation atan engineering site，an approach was developed by simulating the seismic groundmotion at the engineering site，with the constraint of observation seismic data．The theory and the algorithm for the approach were given．A numerical experiment could demonstrate the application of themethod．In the experiment only the quality factor is difficult to determine precisely，other parameters，such as the layer depth，density，shear wave velocity and quality factor values estimated for the buried，were in good agreementwith the targetmodel．

reclamation engineering;underground medium parameters;modeling estimation;seismic ground motion

P315.8

:A

2015－05－07

四川省科技支撑计划项目 (2013SZ0173;2009SZ0026)

韩 超 (1990—)，男，硕士研究生，研究方向:地震地质，122763458@qq.com。

余嘉顺，博士，教授，J.yu@gns.cri.nz。

韩超，付小波，原健龙，等．用地震数据估算填方残留层物性参数的数值试验［J］．桂林理工大学学报，2016，36(4):670－680．

1674－9057(2016)04－0670－11

10.3969/j．issn.1674－9057.2016.04.005