基于Copula-VaR模型的外汇投资组合风险管理

李鹏举

(苏州工业园区服务外包职业学院 人文艺术学院，江苏 苏州　215123)



基于Copula-VaR模型的外汇投资组合风险管理

李鹏举

(苏州工业园区服务外包职业学院 人文艺术学院，江苏 苏州215123)

摘要：随着人民币国际化进程的逐步推进，国际外汇市场的风险性和相依性研究尤为重要.Copula函数作为一个将多元分布建模分解成边缘分布和联合分布的相依结构模型，可解决分布模型难以确定的问题.基于五种货币(即美元、日元、欧元、英镑和港币)日收益数据构建基于AR(2)-GARCH(1，1)-t模型的各个外汇日收益率的边际分布，利用蒙特卡洛方法度量正态Copula函数和t-Copula函数下的投资组合VaR值，为解决外汇市场资产风险问题提供良好的操作与管理决策.

关键词：Copula函数；外汇市场；投资组合；风险价值；蒙特卡洛模拟

Markowitz[1]自1952年提出投资组合管理决策理论以来，采用均值-方差模型的投资组合选择模型较多，但其方差度量上存在诸多问题.Baumol[2]于1963年提出基于VaR法的风险测量模型.随着VaR理论的提出，投资组合风险度量问题在理论研究和业界操作方面取得了极大的进展.在外汇市场中，外汇收益率明显具有非正态分布特征和非线性相依性，且金融时间序列表现出偏态、尖峰和厚尾的统计特征，因此多元正态分布假定下的资产联合分布模型有很大的局限性，采用非正态分布的投资组合风险度量将成为衡量资产分布的重要选择，便于投资组合模型建立和风险度量.

由于多元联合分布的模型构建难度较大，且只有边缘分布相同才能扩展成多元联合分布，因此在联合分布模型构建上形成了长期难以解决的问题.Copula理论的提出有效地解决了这个问题.Copula函数能将不同边缘分布构成多元联合分布，解决了边际分布为非正态分布的问题.

Copula由Sklar[3]于1959年提出，并于20世纪90年代在国外取得了迅速发展.Joe[4]、Nelsen[5]在Copula定义、构造方法和相关性等方面进行了全面详细的介绍；Embrechs等[6]将Copula函数引入金融研究领域.其他一些学者在金融风险计量研究方面取得了丰硕成果，如Rockinger等[7]、Palaro[8]等结合Copula函数和GARCH模型对金融市场的投资组合VaR进行了一系列研究.国内学者对Copula理论的研究较晚，张尧庭[9]最先从理论上讨论了Copula函数；一些国内学者也纷纷对Copula的研究产生了浓厚的兴趣，像张明恒[10]、韦艳华等[11-13]、柏满迎等[14]、史道济等[15]将Copula理论和GARCH模型相结合对金融市场相关性和投资组合选择问题进行了研究.吴振翔等[16]测算了在不同置信水平下欧元和日元对人民币的二元投资组合风险VaR.而对两个以上外汇市场资产组合的风险计量研究还不多，因此研究多个外汇资产组合的风险具有重要意义.

本文首先给出单个资产和投资组合的VaR值的基本概念，并介绍Monte Carlo模拟估计法；然后利用AR-GARCH-t模型对各资产的边缘分布进行估计，在此基础上运用Copula函数对金融资产间的相关性进行度量；最后对比分析正态Copula方法和t-Copula方法的风险度量.

1　Copula理论

Copula可以理解为连接函数，是指对于一个联合分布函数可以分解成多个边缘分布函数和一个Copula函数.

定义1 一个n元Copula函数C是指满足以下性质的多元函数：

1) C是一个函数，[0，1]n→[0，1]；

2) C是一个严格单调递增的函数；

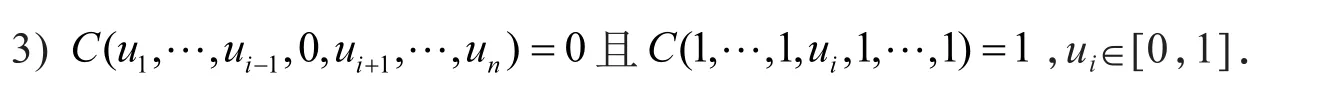
定义2 一个n元联合分布函数F(x1，x2，…，xn)可以由n个连续的边缘分布函数F1(x1)，F2(x2)，…，Fn(xn)和一个Copula函数C表示，即F(x1，x2，…，xn)=C[F1(x1)，F2(x2)，…，Fn(xn)].

从Copula函数的定义可以看出，对于不同边缘分布的模型也可由Copula函数灵活构造其联合分布.

2　蒙特卡洛法与VaR风险度量

2.1蒙特卡洛模拟法

蒙特卡洛模拟法是假设资产价格的变动服从随机过程的动态特征，在一定的时间范围内通过计算机模拟产生随机价格的路径，并依此构建资产收益率分布，进而估计风险值.它不仅涵盖变量的所有可能状况，也可以处理非正态分布模型.

本研究采用多变量随机模型，假设目前投资组合n项资产收益率服从多变量标准正态分布，算法步骤为

Step1，以样本数据估计投资组合n项资产收益率的相关系数矩阵R.

Step2，利用Cholesky分解法分解相关系数矩阵R，得到一个Lower Triangular矩阵A，使得AA'=R.令

且R=AA'，则

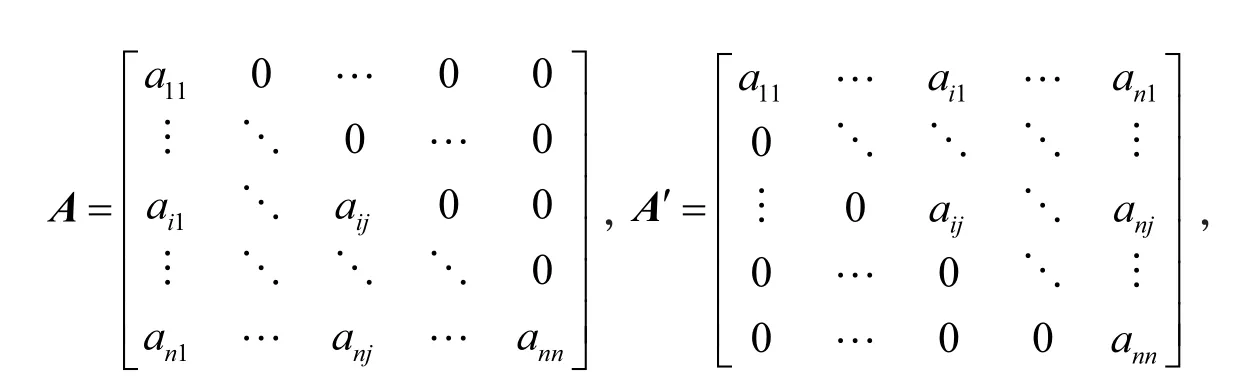
其中矩阵A的元素

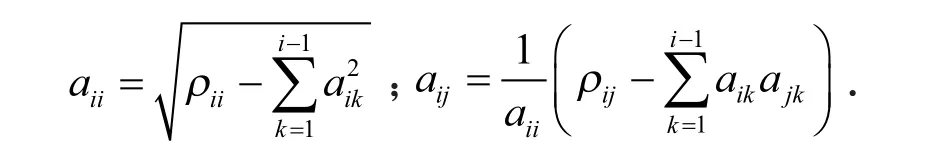
Step3，对标准正态分布N(0，1) 进行随机抽样取出n×1个随机变量，将矩阵A与n×1的随机变量矩阵ε相乘，可求得n个多变量正态随机变量Y，即Y=Aε.

Step4，从取出的随机变量抽样重复进行10 000次Step3，则可得到一连串各资产收益率的预估计值，由此模拟出等权重下的投资组合收益率.

2.2单资产的VaR风险度量

给定概率水平α，单个资产的VaR定义为

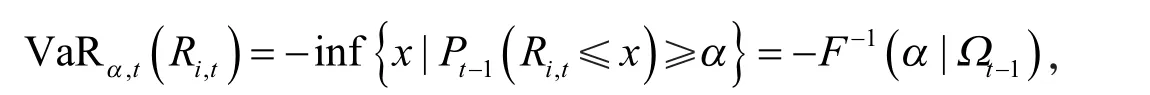
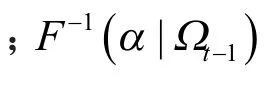
若单个资产收益率服从正态分布或学生t分布，VaR可分别计算

式中：za和tv，a分别为标准正态分布和自由度为v的学生t分布的α分位数；μi，t，σi，t分别为资产i第t天的均值和标准差.

2.3投资组合的VaR风险度量

与单个资产VaR计算类似，正态分布或学生t分布条件下，投资组合VaR可分别计算

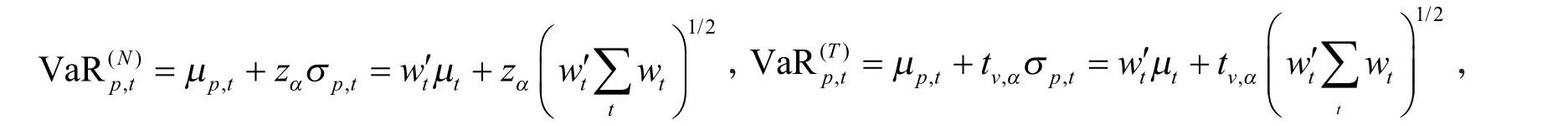
式中wi为第t天投资组合的权重向量.

3　实证分析

3.1数据选取

选取美元(USD)、日元(JPY)、欧元(EUR)、英镑(GBP)和港币(HKD)五种货币指数从2008年1月4日至2011年12月30日的日收盘价作为样本数据，剔除非交易日后得到样本量987个，数据来源http://

3.2投资组合VaR风险度量

对样本采用Eviews7和Matlab2012a软件进行数据分析.描述性统计结果和日收益率频率分布图分别如表1和图1所示.

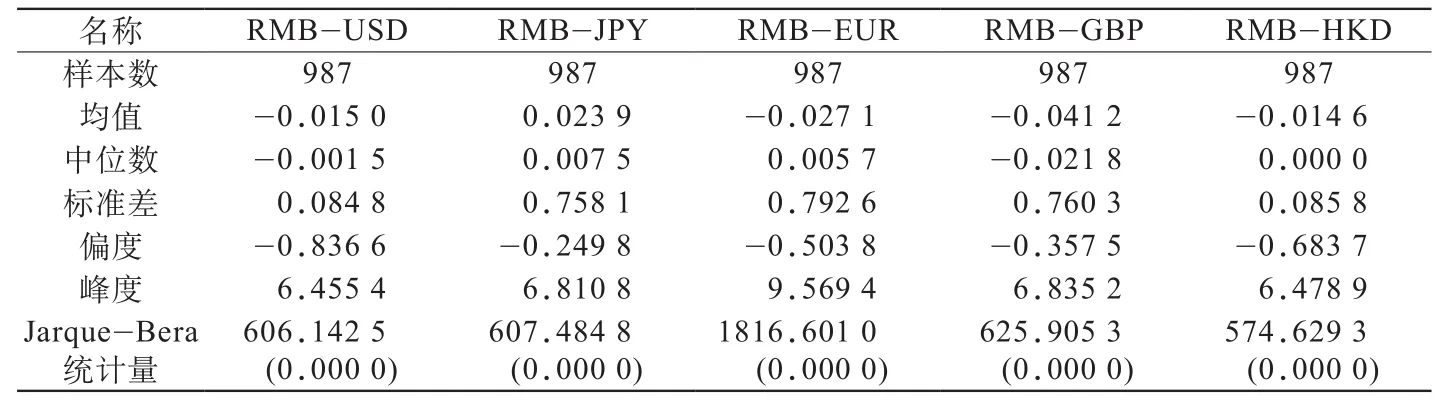
表1　日收益率的描述性统计

从表1中的JB统计量检验结果和图1频率分布图可以看出，日收益率均不服从正态分布，结合峰度和偏度发现服从尖峰厚尾的分布特征，因此采用核光滑方法估计总体分布.日收益核密度估计和经验分布检验如图2所示.

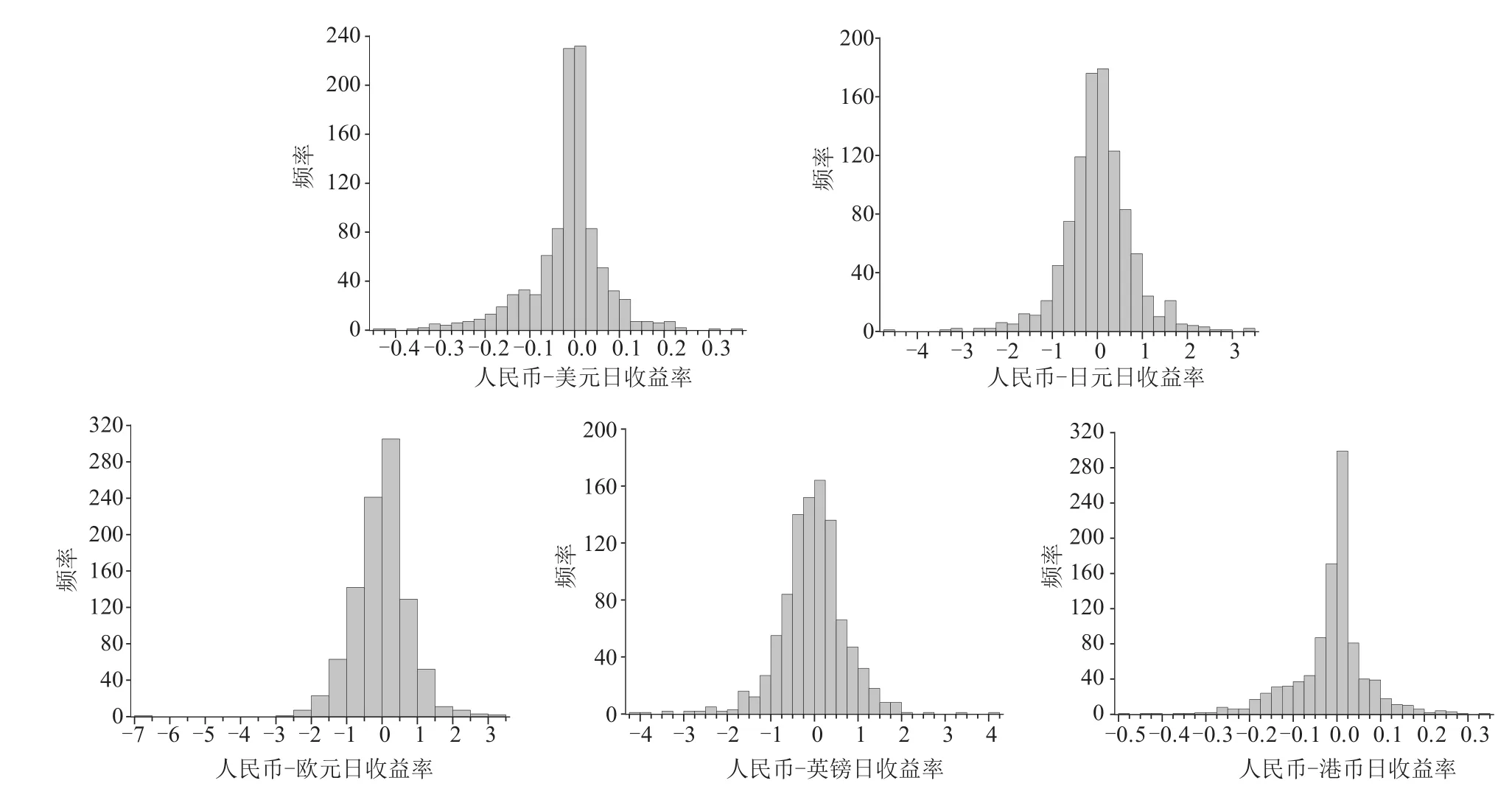
图1　日收益率频率分布图

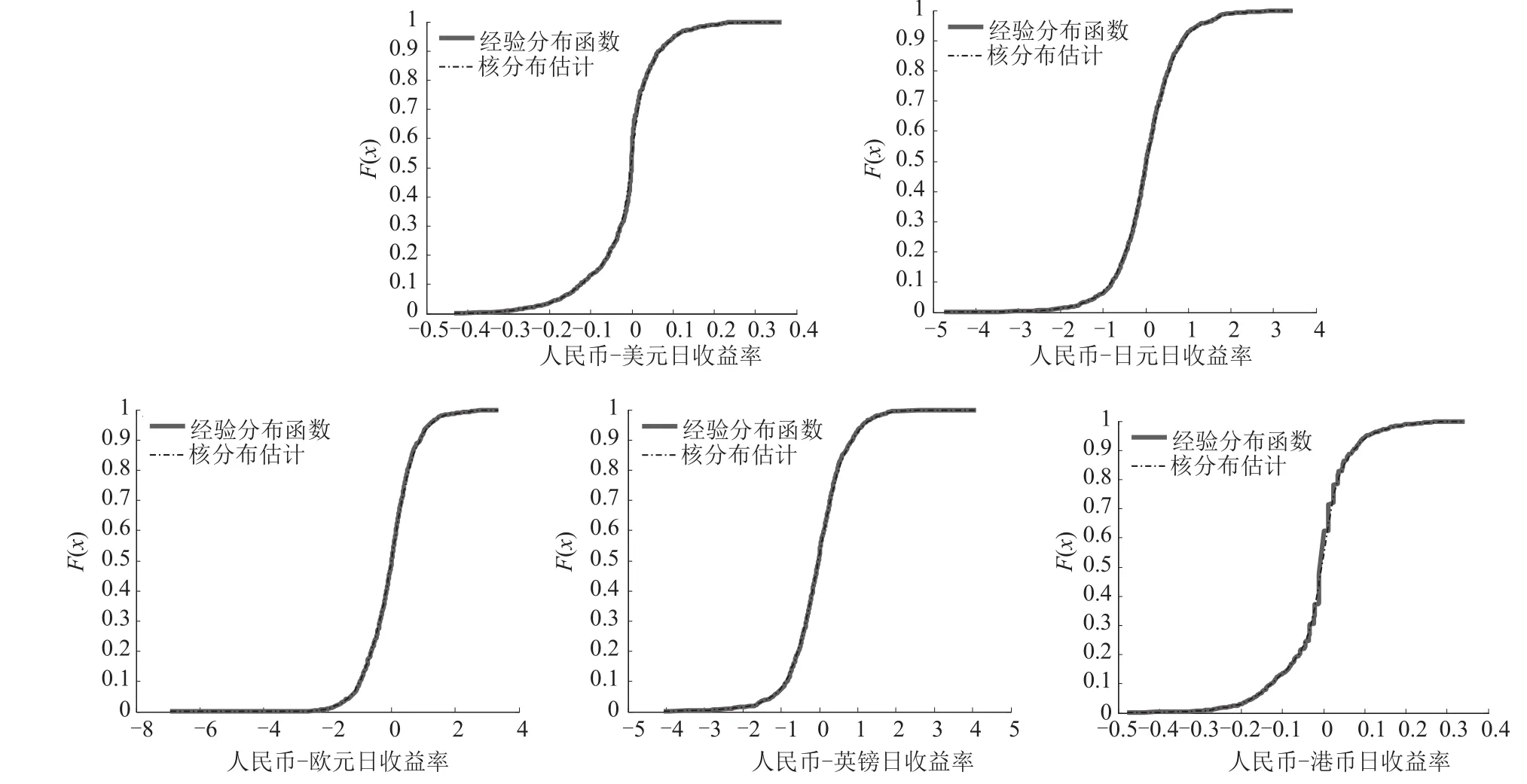
图2　日收益核密度估计和经验分布检验图

从分析结果可以看出，核密度估计检验和经验分布检验图几乎重合.

1) 边缘分布模型.为了避免证券市场的自相关性以及外汇收益率接近学生t分布的特性，因此采用AR(2)-GARCH(1，1)-t模型来估计各个外汇收益的边际分布.其中边际分布模型条件方差估计结果如图3所示.

2) 相依结构模型.为了构建五种外汇之间的相关性，选取正态Copula函数和学生t-Copula函数对资产之间的相依结构进行建模，其线性相关系数如表2和表3所示.通过正态Copula函数和学生t-Copula函数估计外汇市场的线性相关系数，可以采用蒙特卡洛方法计算投资组合的VaR值.

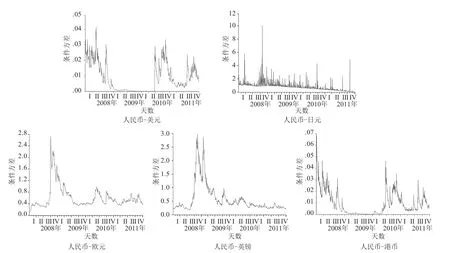
图3　日收益率条件方差估计图

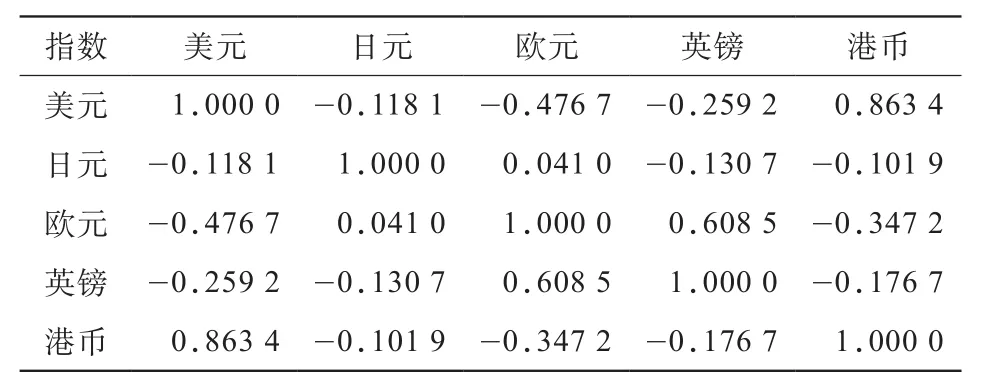
表2　正态Copula函数线性相关系数估计值

表3　学生t-Copula函数线性相关系数估计值

3) 投资组合风险度量.为了检验Copula函数在投资组合VaR风险度量上的效果，不妨假设投资组合为等权的.利用蒙特卡洛方法对正态Copula函数和t-Copula函数下的投资组合VaR进行计算，结果如图4所示(以显著性水平α=0.05为例).

图4　投资组合的VaR计算结果(α=0.05)

可以看出，在α=5％显著性水平的比较中，基于t-Copula方法的VaR值为0.417 7，明显优于正态Copula方法的VaR值为0.507 8.

4　结论

基于Copula函数的特性，讨论多变量联合分布建模问题，研究投资组合VaR风险度量问题.通过对外汇市场的实证研究，分析正态Copula法和t-Copula法在VaR风险度量上的差异，并比较在投资组合模型选择中的优良.研究表明，通过蒙特卡洛方法对Copula函数下的投资组合VaR风险度量，基于学生t分布假设的优化结果比较理想.表明投资组合的收益率得到了提高，降低了外汇市场的风险性.

参考文献：

[1]MARKOWITZ H.Portfolio selection[J].Journal of Finance，1952(7)：77-91.

[2]BAUMOL W J.An expected gain-confidence limit criterion for portfolio selection[J].Management Science，1963(10)：174-182.

[3]SKLARK A.Fonctions de répartition à n dimensions et leurs marges[M].Universite’ de Paris：Publications de l’Institut Statistique de l，1959.

[4]JOE H.Multivariate models and dependence concepts[M].London：Chapman&Hall，1997.

[5]NELSEN R B.An introduction to copulas [M].New York：Springer，1998.

[6]EMBRECHTS P A，MCNEIL A，STRAUMANN D.Correlation：pitfalls and alternatives[J].RISK.，1999，12(5)：11-21.

[7]ROCKINGER M，JONDEAU E.The Copula-GARCH model of conditional dependencies：an international stock market application[J].Journal of International Money and Finance，2006，25(3)：827-853.

[8]PALARO H P，HOTTA L K.Using conditional copula to estimate value at risk[J].Journal of Data Science，2006(4)：93-115.

[9]张尧庭.连接函数(Copula)技术与金融风险分析[J].统计研究，2002(4)：48-51.

[10]张明恒.多金融资产风险价值的Copula计量方法研究[J].数量经济技术经济研究，2004(4)：67-70.

[11]韦艳华.Copula理论及其在多变量金融时间序列分析上的应用研究[D].天津：天津大学，2004.

[12]韦艳华，张世英.金融市场动态相依结构的研究[J].系统工程学报，2006，21(3)：313-317.

[13]韦艳华，张世英.多元Copula-GARCH模型及其在金融风险分析上的应用[J].数理统计与管理，2007，26(3)：432-439.

[14]柏满迎，孙禄杰.三种Copula-VaR计算方法与传统VaR方法的比较[J].数量经济技术经济研究，2007(2)：154-160.

[15]史道济，李瑶.基于Copula的股票市场VaR和最优投资组合分析[J].天津理工大学学报，2007，23(3)：13-16.

[16]吴振翔，叶五一，缪柏其.基于 Copula 的外汇投资组合风险分析[J].中国管理科学，2004，12(4)：1-5.

(责任编辑：沈凤英)

FX Portfolio Optimization Risk Management Using Copula-VaR Model

LI Peng-ju
(School of Arts and Humanities，Suzhou Industrial Park Institute of Services Outsourcing，Suzhou215123，China)

Abstract：With the acceleration of RMB’s globalization， it is particularly important to researchthe risks and the interdependence of the international foreign exchange market.Copulas can be used to decompose multivariate joint distribution into marginal distribution and correlation structure.In this paper we model the actual and joint distribution of daily exchange rate returns of five major currencies，i.e.USD， JPY， EUR， GBP and HKD against RMB mainly based on AR(2)-GARCH(1，1)-t model.The advantage is applied to compute the VaR of a portfolio by Normal and Student’t Copula function.Furthermore，a new model for portfolio choice based on copulas is proposed by Monte Carlo simulation，and empirical analysis is operated in the hope of helping make a strategic decision in the foreign exchange market.

Key words：Copula function；foreign exchange market；portfolio；value at risk；Monte Carlo simulation

作者简介：李鹏举(1980-)，男，河南商城人，讲师，硕士，主要从事数量金融与风险管理研究.

基金项目：江苏省高校哲学社会科学研究基金资助项目(2014SJD607)；苏州市软科学研究资助项目(2014JX54)

收稿日期：2015-09-24；修回日期：2015-10-22

DOI：10.16219/j.cnki.szxbzk.2016.01.009

中图分类号：F830.9

文献标志码：A

文章编号：1008-5475(2016)01-0040-06

引文格式：李鹏举.基于Copula-VaR模型的外汇投资组合风险管理[J].苏州市职业大学学报，2016，27(1)：40-45.