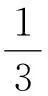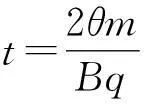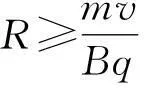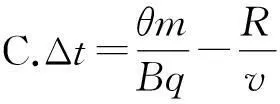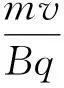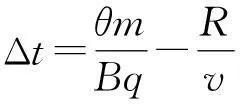从“两个半径的大小关系”入手分析带电粒子在圆形磁场中的运动
李伟康
(芜湖市第一中学 安徽 芜湖 241000)
从“两个半径的大小关系”入手分析带电粒子在圆形磁场中的运动
李伟康
(芜湖市第一中学安徽 芜湖241000)
摘 要:带电粒子在磁场中的运动涉及到的物理知识和方法较多,学生在运动情境的再现和几何关系的寻找上更是感到非常困难.这其中尤其以圆形磁场中的运动问题较难,涉及到两个圆及圆与边的复杂的关系,对粒子运动的约束条件较为隐蔽,此类问题学生感到无从下手.本文从圆形磁场区域半径R和带电粒子轨迹半径r的大小关系入手,详细梳理了粒子在圆形磁场区域中运动的特点,并在解决两个难解例题中加以了应用.
关键词:圆形磁场平行汇聚原理射出区域范围运动最长时间
1当r=R时
本文中r为带电粒子轨迹的半径,R为圆形匀强磁场区域的半径.
此种情况,带电粒子在匀强磁场中的运动有两个互逆的特殊结论,我们形象地称之为“发散平行原理”和“平行汇聚原理”(不计重力等其他非磁场力作用).
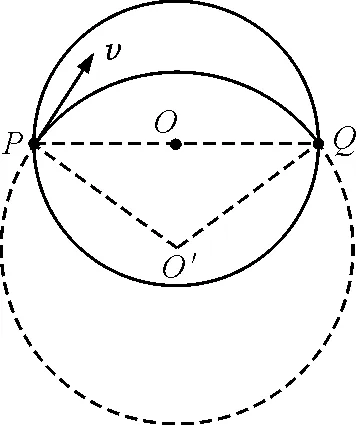
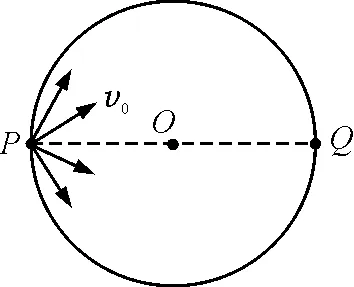
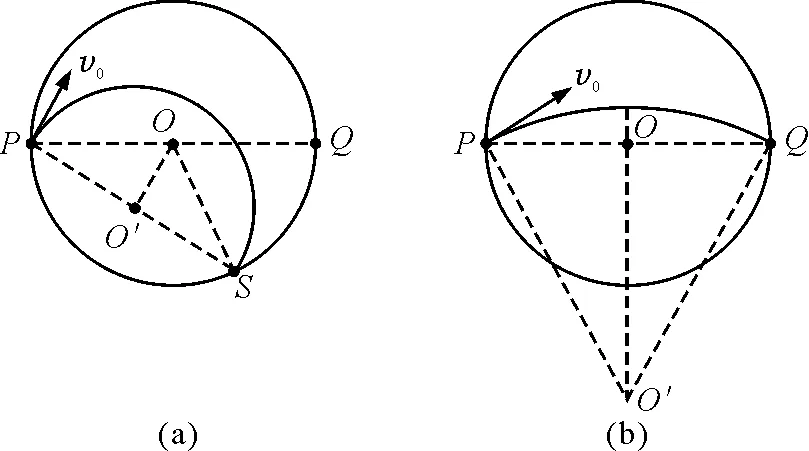
发散平行原理:当一束相同的带电粒子从磁场边界上同一点沿不同方向射入磁场区域,且轨迹半径等于圆形磁场区域半径时,这束粒子将沿同一方向平行射出磁场区域(如图1左图所示).
平行汇聚原理:当一束相同的带电粒子沿同一方向平行射入磁场区域,且轨迹半径等于圆形磁场区域半径时,这束粒子将从磁场边界上同一点射出磁场区域(如图1右图所示).
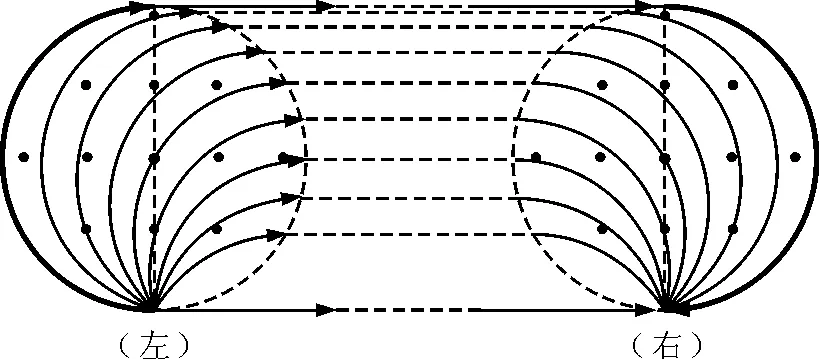
图1
此处不再证明.
(1)出射点分布范围
如图1左图所示,临界状态为粒子刚好沿磁场边界做匀速圆周运动,粒子无法射出磁场.粒子射出磁场的位置(出射点)分布在磁场区域右边半个边界上,即射出区域范围长度刚好为磁场区域周长的一半.
(2)运动最长时间
管理会计的工作较为灵活,工作中没有固定的规范准则,为了将管理会计所具有的的优势充分发挥,就应当重视审计监督。合同管理是企业中财务管理部分的重中之重,企业应当从管理会计的角度出发,分析历史合同中,执行环节存在的问题和相应的责任主体。并且以过去的财务管理体系为基础,对合同管理模式进行调整。最终构建起一套新的财务管理体系。
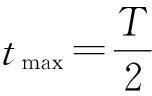
(3)同一出射点对应时间的唯一性
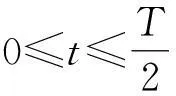
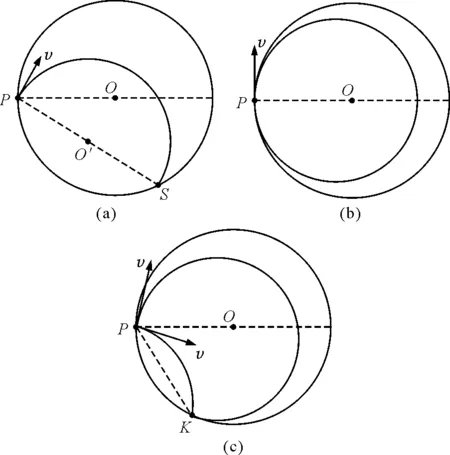
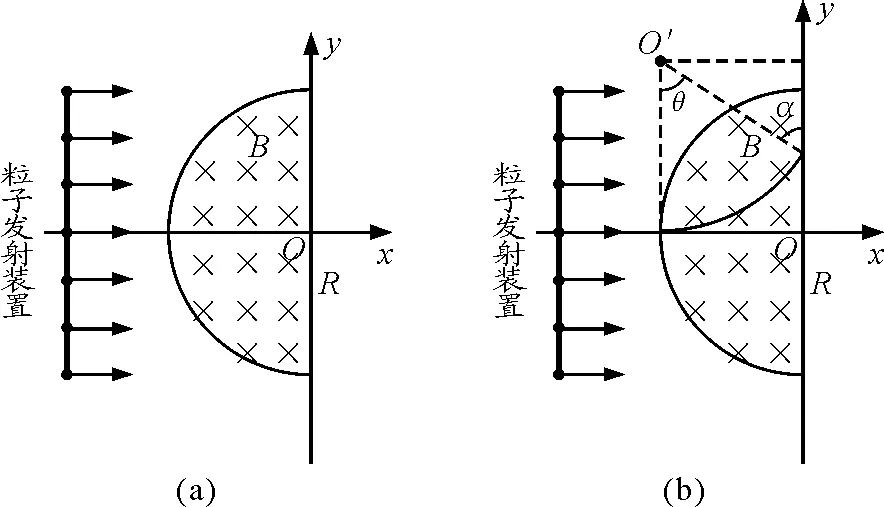
2当r (1)出射点分布范围 当出射点离入射点最远时,该两点的连线(为轨迹圆的弦)最长,最长只能等于轨迹圆的直径,如图2(a)所示.采用“旋转法”分析易知,出射点最近可接近入射点,所以粒子出射点的位置分布在磁场边界PS这段劣弧上. (2)运动最长时间 显然由于r (3)同一出射点对应时间的唯一性 由于r 图2 3当r>R时 采用“旋转法”分析易知,出射点可在磁场边界上任意位置. (2)运动最长时间 对轨迹半径大小确定的粒子,圆心角越大,运动时间越长,此时其轨迹对应的弧长也越长.由于r>R,所以粒子在磁场区域中的轨迹一定为一条劣弧,而对劣弧而言,轨迹弧长越长,其对应的弦长也越长,显然此时最长弦长为磁场区域的直径,如图3所示. 图3 (3)同一出射点对应时间的唯一性 由于r>R,所以在磁场区域中粒子运动轨迹只能为劣弧.磁场边界上同一出射点对应唯一的运动时间. 图4 图5 点评:本题中两种情况涉及到的粒子初速度方向和轨迹半径均不具有直观可比性,学生甚至画不出粒子对应的运动轨迹,感到无从下手.若有本文中前述规律为基础,本题的分析则显得较为顺利,从而可轻松求解. 【例2】如图6(a)所示,半径为R的半圆形区域内分布着垂直纸面向里的匀强磁场,磁感应强度为B,半圆的左边垂直x轴放置一粒子发射装置,在-R≤y≤R的区间内各处均沿A轴正方向同时发射出一个带正电粒子,粒子质量均为m,电荷量均为q,初速度均为v,重力及粒子间的相互作用均忽略不计,所有粒子都能到达y轴,其中最后到达y轴的粒子比最先到达y轴的粒子晚Δt时间,则 图6 A.粒子到达y轴的位置一定各不相同 点评:若不知道“在圆形匀强磁场区域中,当粒子轨迹半径等于磁场区域半径时,平行射入的粒子会汇聚于磁场边缘一点”,本题的分析是很难展开的. Analysis on the Charged Particles Motion in A Circular Magnetic Field based on The Size of Relationship between The Two Radii Li Weikang (Wuhu No.1 Senior School,Wuhu,Anhui241000) Abstract:Many physical knowledge and methods are covered in the movement of charged particles in a magnetic field. Students may find difficulty handling problems of reproduction and geometric relation of the moving cases above. Especially, the problems related to the moving case of circular magnetic field which cover the complex relationship between two circles and between the circle and side are very difficult. Besides, the constraint conditions on the particle motion are more obscure. In this article, starting from the relationship between the magnitude of circular magnetic field with radius "R" and the trajectory of a charged particle radius "r", the characteristics of the moving particle in a circular magnetic field are analyzed and two difficult examples are solved to further illustrate the application. Key words:circular magnetic field; the principle of parallel convergence; the range of the injection region; the longest time of motion. (收稿日期:2015-07-15)