横看成岭侧成峰——对一竞赛试题多种解法的赏析

黄国超

(诸暨市草塔中学　浙江 绍兴　311812)



横看成岭侧成峰——对一竞赛试题多种解法的赏析

黄国超

(诸暨市草塔中学浙江 绍兴311812)

摘 要：本文以一道运动学题为例,谈谈“一题多解”在物理教学中的应用,通过一题多解的教学设计激发学生兴趣,开拓学生思路,培养逻辑推理能力和想象力,进一步培养学生的解题能力.并结合例题探讨了在一题多解教学中应该遵循的一些原则.

关键词：一题多解物理教学

一题多解对于培养学生从不同角度、不同侧面去分析问题、解决问题很有益处，它有利于调动学生思维的积极性，锻炼学生思维的灵活性，培养学生思维的创造性．但一题多解的最终目的不是用来展示本题有多少种解决问题的途径，也不是所有的题目都需要用多种方法去解决，而是要灵活运用解题方法，寻找一种最佳、最近的途径，也就是说，掌握“一题多解”的最终目的是为了“拓展思维空间，培养学习兴趣”．

【题目】如图1，海岛城市A离海岸120km，海滨城市B离C点160km，已知路上汽车速度是海上轮船速度的2倍，要使A和B两城市之间运输时间最少，转换码头D建在何处最佳？

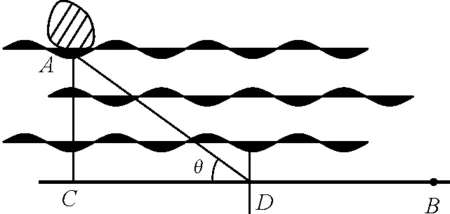
图1

解析：该题的关键是寻找一条用时最短的路径，我们可以用几何方法来确定运输的可能路径．

第一条路径：码头建在B城市，直接入水以v2速度在海上运输．此路程最短，但海上运输速度较岸上小．

第二条路径：码头建在C点，先沿岸以速度v1到C点，再垂直岸路线到A城市，此路径利用了岸上速度较大，但路程最长．

第三条路径：码头建在BC之间某点D，先沿岸到D，再沿与岸成θ角的路线到达A城市．

上述哪条路径用时最短呢？我们不防先通过比较来说说哪种路径用时会比较短．

如图2所示，一条路径BB′A，点B′是靠近B左面的一点，所以Δθ很小，与岸的夹角为θ+Δθ，设所需时间t1．另一条路径BA，设与岸成θ角，所需时间t2．

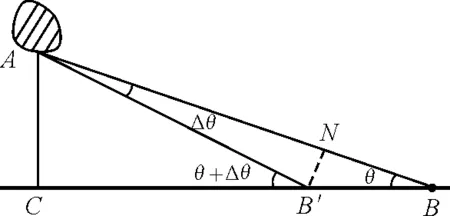
图2

过B′作辅助线B′N，使AN=AB′，由于Δθ很小，可近似认为B′N⊥AB，则BN=BB′cosθ，那么两路径所需时间差即为分别通过BN与BB′所用时间的差值

现在的问题就在于具体的B′在哪里？与岸边线的夹角多大？下面我们就介绍几种求解方法来分析这一问题．

解法1：图像解析法

如图3所示，设运动总时间为Δt，在岸上运动时间为Δt1，在海中运动时间为Δt2．若直接在B点下水，则Δt=Δt2，能到达的最前方位置将是以B为圆心，v2Δt为半径的一个圆周位置；若将所有时间都用在了岸上，则在海上已无时间再前进，能到达的最前方是以B为圆心，v1Δt为半径的圆周位置，岸边即图中的B1位置．若在岸边的其他任意一点D下水，能到达的最前方位置是以D为圆心，v2Δt2为半径的圆周．若下水点从B到B1，由于总时间确定，则岸上运动时间将线性增加，而海中运动时间将线性减小，所以水中前进的半径变化是线性的，这样的许许多多的圆组成的最前方的界线为一直线，即图中的NN′为入水后的与前进范围圆相切的直线(实为无数个圆弧的包络线)．要想到达最前面的边界线的时间最短，海中运动方向DA必须垂直包络线(如图3)，此时，运动方向与岸边直线的夹角即为本题前面所要寻找的θ角．

图3

已知条件v1=2v2，结合图像可求得θ=60°

点评：这种解法新颖、直观、简便，构思巧妙；但由于技巧性较强，一般学生较难想到．

解法2：微元极值法

从B点出发，先沿岸运动到D，再下水到达A城市，设∠CDA=θ时的路径所需时间为最短，这种方法中只要时间取极小值即可．如图4所示.

图4

若有一条路径在D点前方很短距离的H点下水，这条路径与D下水相比，只是在岸上多运动了DH距离，而在海上少运动DI距离(作辅助线HI，取AH=AI，因为DH取非常小，可近似认为HI⊥DI，DI=DHcosθ)．

设DH距离用时Δt1，DI距离需时间Δt2，则

DH=v1Δt1DI=v2Δt2

两路径的时间差

而另一条路径是在D点后方很短距离的K点下水，这一路径将在岸上少运动DK距离，但在海中多运动了KM距离．(与前面一样，这里可近似认为KM=JD=DKcosθ)

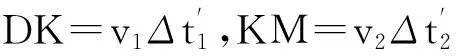
所以两路径的时间差

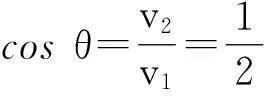
点评：微元法是分析、解决物理问题中的常用方法，也是从部分到整体的思维方法．用该方法可以使一些复杂的物理过程用我们熟悉的物理规律迅速地加以解决，使所求的问题简单化．在使用微元法处理问题时，需将其分解为众多微小的“元过程”，而且每个“元过程”所遵循的规律是相同的，这样，我们只需分析这些“元过程”，然后再将“元过程”进行必要的数学方法或物理思想处理，进而使问题求解．使用此方法会加强我们对已知规律的再思考，从而引起巩固知识、加深认识和提高能力的作用．

解法3：函数解析法

如图5所示 ，设码头建在D点，AD与岸的夹角为θ，所需时间为t，可列式得

图5

有数学万能公式可得

代入上式，可得到当θ=60°时t取最小值．则

所以

点评：解析法是几何问题的代数处理．这种方法思路清晰、解法简捷，利用了数学的函数取极值方法．这里运用了三角函数代换公式，其实也可利用对函数求导取极值的方法来求解θ值．

解法4：等效替代法

如图6所示 ，先从B城市出发沿岸到D点用时Δt1，再下水到A城市用时Δt2．则有

BD=v1Δt1DA=v2Δt2

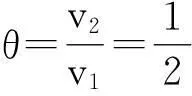
图6

点评：掌握等效替代法及应用，体会物理等效思想的内涵，有助于提高考生的科学素养，初步形成科学的世界观和方法论，为终身的学习、研究和发展奠定基础．新高考的选拔愈来愈注重考生的能力和素质，其命题愈加明显地渗透着物理思想、物理方法的考查，等效思想和方法作为一种迅速解决物理问题的有效手段．

解法5：费马原理法

把CB设想为空气和水的分界面，光在空气中的速度为v1，在水中的速度为v2，则当A发出的光以θ人射到界面上，根据费马原理可知A→D→B是光线由A传到B的费时最小的路径，即光从A传到D后，在界面上发生折射，折射光线为DB时所用时间为最短，所以满足

可见，要使A，B两城市之间运输时间最少，转换码头D与海岛城市A的连线与海岸的夹角θ为60°，则

所以

点评：直接利用原理，最易被学生所接受．

一题多解是以培养学生多解意识，拓展学生解题思路，激发学生的发散性思维，诱导学生积极开展思维为主要目的．不同层次的学生可以选择不同的方法去思考．

(收稿日期：2015-10-22)