基于磁力等效原理的刚性磁悬浮转子系统高精度在线动平衡
刘 超 , 刘 刚, 盖玉欢
(1.北京航空航天大学 仪器科学与光电工程学院,北京 100191; 2. 北京航空航天大学 惯性技术重点实验室,北京 100191;3. 北京航空航天大学 新型惯性仪表与导航系统技术国防重点学科实验室,北京 100191)
基于磁力等效原理的刚性磁悬浮转子系统高精度在线动平衡
刘超1,2,3, 刘刚1,2,3, 盖玉欢1,2,3
(1.北京航空航天大学 仪器科学与光电工程学院,北京100191; 2. 北京航空航天大学 惯性技术重点实验室,北京100191;3. 北京航空航天大学 新型惯性仪表与导航系统技术国防重点学科实验室,北京 100191)
摘要:针对磁悬浮飞轮转子不平衡振动问题,提出了一种在线动平衡方法。其基于磁轴承控制作用力与转子不平衡离心力之间的等效原理,通过检测磁轴承的控制作用力解算转子不平衡校正质量。设计了零位移控制器,使转子绕几何轴旋转,此时磁轴承的控制作用力与控制电流呈线性关系,通过测量控制电流来准确获得磁轴承的控制作用力。该方法消除了传统方法由动力学模型过度简化带来的误差,尤其适用于强陀螺效应的扁平型刚性磁悬浮转子系统。实验验证了该方法的有效性,对提高磁悬浮转子系统的动平衡精度具有实际意义。
关键词:刚性转子;主动磁轴承;不平衡振动;在线动平衡
主动磁轴承(简称磁轴承)通过可控电磁力对转子进行悬浮支承,具有无摩擦、无需润滑、容许转子转速高等特点,在高速旋转机械中得到大量应用[1]。
旋转机械中转子质量不平衡是机械振动故障的重要来源[2-4]。在磁悬浮转子系统中,转子质量不平衡不仅产生振动、噪声,还会引起额外的响应电流,增加系统功耗,使功放提前饱和,降低磁轴承控制系统的稳定性[5]。针对磁悬浮转子系统的不平衡振动问题,主要有两种解决途径:自动平衡控制和转子动平衡。自动平衡控制通过消除磁轴承对转子不平衡的响应,使转子绕惯性主轴旋转,适用于对转子几何轴跳动无严格要求的旋转机械[6-7]。转子动平衡通过对转子不平衡进行校正,使转子的惯性主轴与几何轴重合,有效降低转子的不平衡振动。对于磁悬浮转子系统,除了在动平衡机上进行离线动平衡外,还有一种现场动平衡方法:在线动平衡[8]。在线动平衡利用磁轴承控制系统自身集成的传感器单元和电磁力控制单元,根据转子的不平衡响应解算转子的不平衡量。Li等[9]应用传统的影响因数法实现转子的在线动平衡,需要多次试重,动平衡效率低。韩辅君等[10]根据磁轴承转子系统的不平衡响应直接计算转子不平衡量,虽然不需试重,但是受磁轴承转子系统模型的非线性影响,动平衡精度受限。王英广等[11]通过对转子进行零位移控制消除了磁轴承控制力的非线性,但是,其基于陀螺力学方程的推导需要忽略陀螺效应项,只适用于细长轴转子,对于磁悬浮飞轮、磁悬浮控制力矩陀螺等具有强陀螺效应的扁平型转子无法直接应用。本文以磁悬浮飞轮为研究对象,提出了基于磁力等效原理的刚性转子在线动平衡方法。对转子实施几何轴的零位移控制,通过检测磁轴承控制电流得到磁轴承控制作用力,将磁轴承控制作用力等效为磁轴承平面上的虚拟不平衡校正质量,再经过换算得到校正平面上的不平衡校正质量。本方法不需试重,可用于强陀螺效应刚性磁悬浮转子系统的动平衡。
1磁力等效原理与磁力表达式
1.1磁力等效原理
转子的动不平衡是指转子质量分布不均匀导致惯性主轴与理想旋转轴不重合,而通常这个理想的旋转轴为转子几何轴。转子的动不平衡可进一步分解为静不平衡和偶不平衡[12]。静不平衡是指转子质心相对于旋转中心的偏移;偶不平衡是指惯性主轴相对于几何轴的偏转。在刚性磁悬浮转子系统中,当磁轴承控制转子绕几何轴匀速转动时,磁轴承对转子的控制作用力与转子的动不平衡之间具有某种特定的关系,本文提出两个论断:① 控制转子绕某点转动的外部作用力等于转子相对于该点的静不平衡校正质量的离心力;② 控制转子绕某固定轴做匀速转动的外力矩等于转子相对于该轴的偶不平衡校正质量的离心力矩。将其称为磁力等效原理,并基于此等效原理进行转子的在线动平衡。
1.2磁轴承磁力表达式
实际的磁轴承系统中,磁轴承都采用差动形式输出电磁力,磁力表达式为[1]
(1)
式中:N0为线圈匝数,A0为磁极面积,μ0为真空磁导率,i0为偏置电流,i为控制电流,x0为单边气隙长度,x为转子位移。将式(1)在平衡位置i=0、x=0处泰勒展开得
famb≈kii+kxx
(2)
式中:ki为电流刚度,kx为位移刚度。ki、kx表达式为
(3)
由式(1)可知磁轴承磁力是控制电流和转子位移的强非线性函数,式(2)所示的线性化公式的准确度与转子所处的位置有关。当控制转子绕几何轴旋转时,即x=0,根据式(1)得
famb=kii
(4)
此时磁轴承磁力是控制电流严格的线性函数,这就意味着可以通过控制电流准确获得磁轴承磁力。
2校正质量的解算
假设转子在A、B两端磁轴承的控制作用下绕几何轴旋转,磁轴承A和磁轴承B对转子的控制力可以简化为一个过质心的合力和一个合力偶。根据磁力等效原理,此合力与转子的静不平衡校正质量的离心力等效;此合力偶对转子的力矩与转子的偶不平衡校正质量的离心力矩等效。根据刚性转子动平衡原理[12],转子的静不平衡和偶不平衡可以等效为两个动平衡面上的不平衡。选择磁轴承A、B平面为动平衡面,由于不平衡量的分解合成与磁力的分解合成过程相同,因此可以将磁轴承A、B的磁力直接等效为磁轴承平面上的虚拟校正质量。然后由虚拟校正质量解算校正面上的校正质量的大小与相位。
图1是磁悬浮转子二平面动平衡示意图。转子几何轴从左到右依次穿过校正面Ⅰ、磁轴承A平面、转子质心、磁轴承B平面和校正面Ⅱ。校正面Ⅰ、磁轴承A平面、磁轴承B平面和校正面Ⅱ到质心的距离分别为l1、la、lb和l2,相邻两个平面的距离分别为L1、L2、L3。校正面Ⅰ和校正面Ⅱ的距离为L。磁轴承A、B的控制力矢量分别为fa、fb,转子旋转角速度为ω。

图1 转子动平衡示意图Fig.1 Schematic of rotor balancing
磁轴承A、B平面上的等效不平衡校正量为
(5)
将磁轴承A、B平面上的不平衡校正量转换为校正面Ⅰ、校正面Ⅱ上的不平衡校正量为
(6)
设校正面Ⅰ、Ⅱ上校正质量所在圆的半径分别为r1、r2,则由校正质量大小及所在相位构成的矢量为
(7)
将式(5)、式(6)代入式(7)得
(8)
其中,磁轴承控制力fa、fb根据式(4)由磁轴承控制电流计算获得;K为转换矩阵,可以表示为
(9)
3零位移控制器设计
转子几何轴的零位移控制是实现基于磁力等效原理的转子动平衡的基础。国内外对零位移控制方法有大量的研究,本文采用通用陷波器[13]的原理,在传统稳定控制器的基础上增加零位移控制器,实现转子绕几何轴旋转。
3.1磁轴承控制系统模型
对于理想的磁悬浮转子,转子几何轴与惯性主轴重合,在转子惯性主轴固定坐标系中,结合陀螺技术方程可以得到控制系统模型为

(10)
式中:q=[x,-β,y,α]T为转子惯性主轴广义坐标向量,qs为几何轴的广义坐标向量;M=diag(m,Jr,m,Jr),m为转子质量,Jr为转子赤道转动惯量;Ki=diag(kiax,kibx,kiay,kiby),Kx=diag(kax,kbx,kay,kby),其元素分别为A、B两端磁轴承磁力线性化后的电流刚度和位移刚度;
式中:H=Jzω,为转子沿Z轴的角动量,Jz为转子极转动惯量;
其元素为电流环传递函数,假设各路磁轴承参数相同,kf为电流环放大倍数,L为线圈电感,R为线圈电阻;ctrl(·)为磁轴承闭环控制器。系统的控制框图如图2所示。

图2 磁轴承控制系统框图Fig.2 Block diagram of AMB control system
当磁悬浮转子具有动不平衡时,转子几何轴与惯性主轴的关系可以近似表示为
q=qs+qe
(11)
式中,qe为不平衡偏移向量。qe可表示为
(12)
式中,e为转子质心相对于几何中心偏移的大小,φ为偏移的初始相位;egi为转子惯性主轴相对于几何轴偏转角位移的大小,γ为偏转的初始相位。
将式(11)代入式(10)得
(13)
由式(13)可知,转子的动不平衡可以等效为一个附加同频扰动。基于式(10)所描述的理想转子模型设计的控制器ctrl(·)不能完全克服同频扰动,转子的几何轴含有同频位移响应。因此,需要设计零位移控制器实现转子几何轴的零位移控制。
3.2零位移控制器设计
为消除几何轴广义坐标向量qs的同频扰动响应,在四路反馈信号进入控制器ctrl(·)前各增加一个基于通用滤波器的零位移控制器,实现同频反馈增益的无穷大。

图3 零位移控制器结构框图Fig.3 Block diagram of zero-displacement controller
图3为一路零位移控制器的结构框图。它由一条同频滤波器Nf通路与一条单位前向通路并联组成,ε为深度控制参数。Nf对输入信号的同频成分具有积分累加作用,其输出可以看作同频信号发生器,用于克服同频扰动。只要系统闭环渐进稳定,则Nf输入信号中一定不含同频成分,即实现零位移控制。
为证明系统稳定性,将四路零位移控制器写成向量的形式,并参照文献[13]的证明思路将控制系统写成如图4的形式。
(14)

图4 灵敏度函数与滤波器闭环Fig.4 Close loop of sensitivity S(s) and filter Nf(s)
S(s)为由给定误差到实际误差的传递函数矩阵,由控制器ctrl(.)保证其是稳定的,即特征根都有负实部。系统闭环特征多项式为
det(I+εNf(s)S(s))=0
(15)
将式(14)代入式(15)得

(16)

(17)
当ε=0时,有s(0)=±jω。定义T=TR+jTJ,则U(jω)=TS(jω)。对式(17)在s=jω,ε=0处求偏导得
(18)
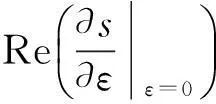
4实验验证
利用图5所示的北京航空航天大学研制的基于磁悬浮支承的反作用飞轮FW68样机进行实验验证。磁轴承控制系统采用TMS320C31+FPGA数字控制系统,采样周期为150 μs,功放采用PWM调制,载波频率为20 kHz。转子的绝对位置参考相位由外加光电传感器给出。实验样机的主要设计参数如表1所示。

图5 磁悬浮反作用飞轮FW68Fig.5 Magnetically suspended reaction flywheel-FW68

参数量值参数量值ω/(r·min-1)±5000H/(N·ms)68m/kg9.35Jr/(kg·m2)0.0748kx/(N·m-1)6.68×105Jz/(kg·m2)0.129ki/(N·A-1)300L1/m0.0095L2/m0.045L3/m0.0095r1/m0.1445r2/m0.1445
为方便实验进行,在不抽真空条件下转子转速为3 000 r/min时进行动平衡实验。对转子进行零位移控制后,待转子位移收敛到零,求得同频控制电流为
ia=(0.087 4-j0.021 0)A
ib=(0.067 9+j0.080 9)A
由式(8)解得校正质量为
m1=(1.778-j0.124)g
m2=(1.489+j1.384)g
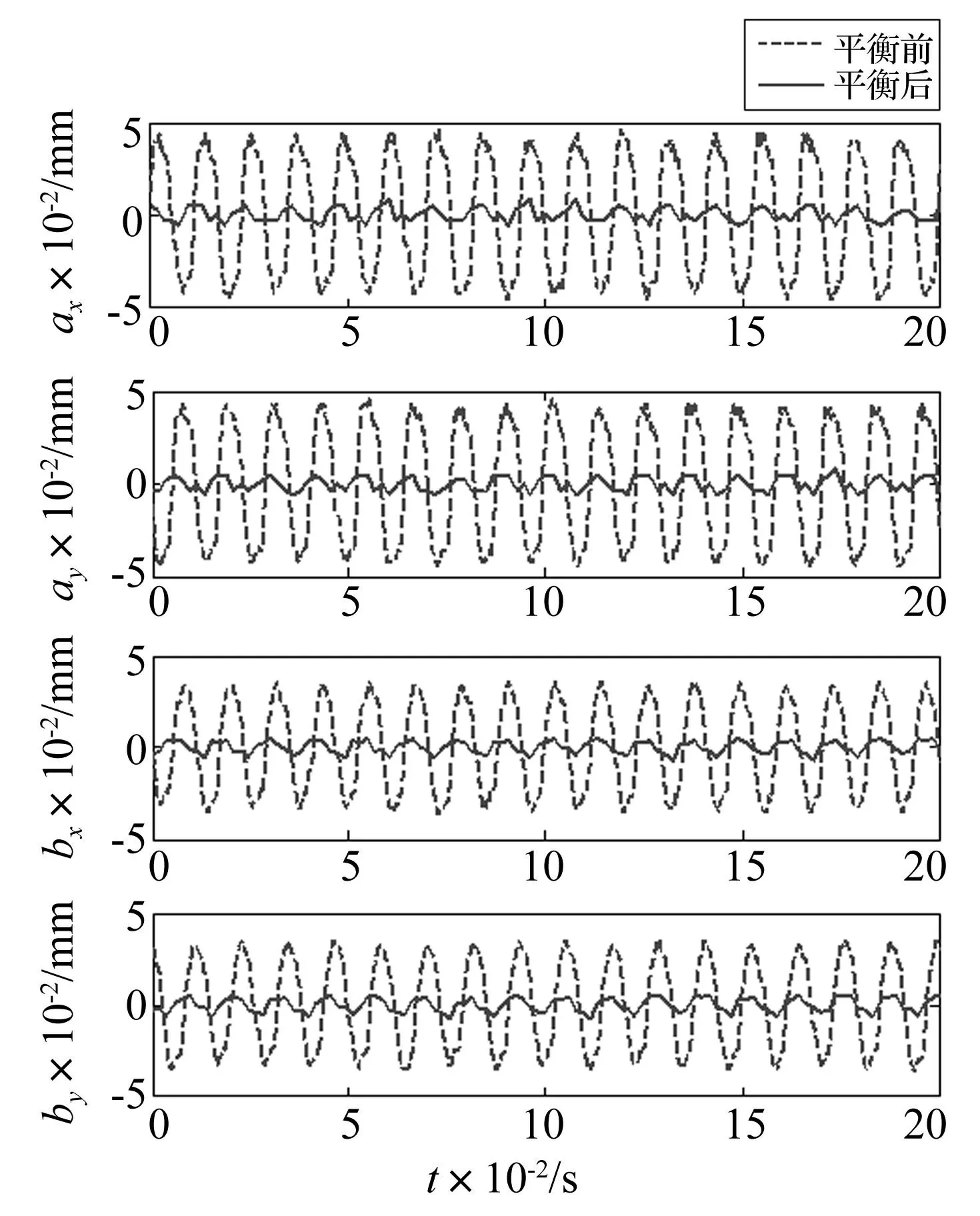
图6 动平衡前后转子位移Fig.6 Rotor displacements before and after dynamic balancing
对转子进行加重配平后,再次进行升速实验。图6、图7为在额定转速5 000 r/min时动平衡前后转子位移和控制电流变化对比图,转子同频位移跳动峰峰值由动平衡前的80 μm降低为动平衡后的15 μm,降低了81.3%;控制同频电流变化峰峰值由动平衡前的0.18 A降低为动平衡后的0.022 A,降低了87.8%。转子动平衡效果显著。
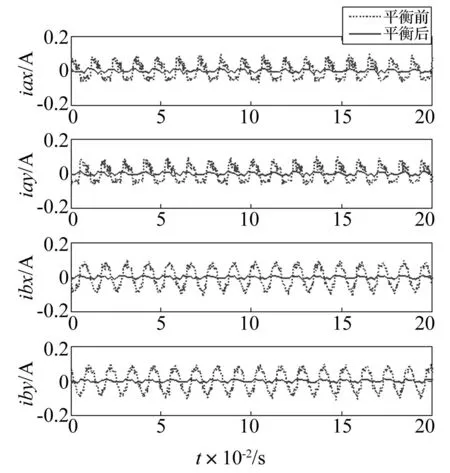
图7 动平衡前后控制电流Fig.7 Control currents before and after dynamic balancing
5结论
本文提出了一种基于磁力等效原理的刚性转子动平衡方法。通过在传统控制器基础上增加零位移控制器,实现了转子几何轴的零位移控制。在零位移控制状态下,磁轴承的电磁力与控制电流成线性关系。通过检测控制电流获得磁轴承的电磁力,根据质量校正公式解算校正质量。最后通过实验验证了本方法的有效性。本方法的特点可以概括为以下几点:
(1) 基于磁力等效原理的刚性磁悬浮转子动平衡方法可以用于强陀螺效应的扁平型转子的在线动平衡。
(2) 零位移控制容易实现,通过检测控制电流获得磁轴承力,检测精度高不需要力传感器。
(3) 一次启车,不需要试重,动平衡效率高。
参 考 文 献
[ 1 ] 房建成,孙津济,樊亚洪. 磁悬浮惯性动量轮技术[M]. 北京:国防工业出版社,2012.
[ 2 ] 黄立权,王维民,苏奕儒,等. 刚性转子自动平衡寻优控制方法与实验研究[J]. 振动与冲击,2011, 30(5): 101-105.
HUANG Li-quan, WANG Wei-min, SU Yi-ru, et al. Optimal control method and test for rigid rotor auto-balancing[J]. Journal of Vibration and Shock, 2011, 30(5): 101-105.
[ 3 ] 王维民,高金吉,江志农,等. 旋转机械无试重现场动平衡原理与应用[J]. 振动与冲击,2010, 29(2): 212-215.
WANG Wei-min, CAO Jin-ji, JIANG Zhi-nong, et al. Principle and application of no trial weight field balancing for a rotating machinery[J]. Journal of Vibration and Shock, 2010, 29(2): 212-215.
[ 4 ] 黄树红,徐煜兵,贺国强,等. 多功能轴系动平衡及振动分析系统[J]. 振动与冲击,2000, 19(1): 79-84.
HUANG Shu-hong, XU Yu-bing, HE Guo-qiang, et al. Intelligent integrated system for dynamic balance, vibration measurement and analysis[J]. Journal of Vibration and Shock, 2000, 19(1): 79-84.
[ 5 ] Zhang S W, Gu Z H, Zhang Z J. Dynamic balancing method for the single-threaded, fixed-pitch screw rotor[J]. Vacuum, 2013, 90: 44-49.
[ 6 ] 刘彬,房建成,刘刚,等. 磁悬浮飞轮不平衡振动控制方法与试验研究[J]. 机械工程学报,2010, 46(12): 188-194.
LIU Bin, FANG Jian-cheng, LIU Gang, et al. Unbalance vibration control and experiment research of magnetically suspended flywheels[J]. Journal of Mechanical Engineering, 2010, 46(12): 188-194.
[ 7 ] 韩邦成,催华,汤恩琼. 基于滑模扰动观测器的磁轴承主动振动控制[J]. 光学精密工程,2012, 20(3): 563-570.
HAN Bang-cheng, CUI Hua, TANG En-qiong. Vibration suppression of magnetic bearing based on sliding mode disturbance observer[J]. Optics and Precision Engineering, 2012, 20(3): 563-570.
[ 8 ] 李伟华,曹国恩,刘剑锋. 高速电机转子现场动平衡方法建模与仿真[J]. 航空精密制造技术,2013, 49(5): 21-25.
LI Wei-hua, CAO Guo-en, LIU Jian-feng. Field balancing modeling and simulation of high-speed rotor[J]. Aviation Precision Manufacturing Technology, 2013, 49(5): 21-25.
[ 9 ] Li H W, Xu Y, Gu H D, et al. Field dynamic balance method study for the AMB-flexible rotor system[C]//Transactions of the 19th International conference on Structural Mechanics on Reactor Technology, Toronto, Canada, 2007: 1-7.
[10] 韩辅君,房建成. 磁悬浮飞轮转子系统的现场动平衡方法[J]. 航空学报,2010, 31(1): 184-190.
HAN Fu-jun, FANG Jian-cheng. Field balancing method for rotor system of a magnetic suspending flywheel[J]. ACTA Aeronautical et Astronautic Sinica, 2010, 31(1): 184-190.
[11] 王英广,房建成,郑世强,等. 磁悬浮电机的高效高精度在线动平衡[J]. 光学精密工程,2013, 21(11): 2884-2892.
WANG Ying-guang, FANG Jian-cheng, ZHENG Shi-qiang, et al. Field balancing of magnetically levitated motor in high-efficiency and high-accuracy[J]. Optics and Precision Engineering, 2013, 21(11): 2884-2892.
[12] 郭俊华. 刚性转子动平衡技术及系统研究[D]. 昆明:昆明理工大学,2012.
[13] Herzog R, Philipp B,Gahler C,et al. Unbalance compensation using generalized notch filers in the multivariable feedback of magnetic bearings[J]. IEEE Transaction on Control Systems Technology, 1996, 4(5): 580-586.
Field balancing for a magnetically suspended rigid rotor based on magnetic forces equivalence principle
LIUChao1,2,3,LIUGang1,2,3,GEYu-huan1,2,3
(1. School of Instrument Science and Opto-electronic Engineering, Beihang University, Beijing 100191, China;2. Science and Technology on Internal Laboratory, Beihang University, Beijing 100191, China;3. Fundamental Science on Novel Inertial Instrument & Navigation System Technology Laboratory, Beihang University, Beijing 100191, China)
Abstract:A field balancing method was proposed to solve rotor unbalance vibration problems in a magnetically suspended flywheel (MSFW). Based on the equivalence principle between magnetic control force and unbalance centrifugal force, the rotor unbalance was calculated and corrected by measuring the magnetic forces. A zero-displacement controller was designed to make a rotor rotate around its geometric axis. Then the controlling force of the magnetic bearing was obtained by measuring the control current since the former was a linear function of the latter. This method eliminated the errors introduced by the oversimplification of dynamic model in conventional methods and it was especially applicable for a high-gyroscopic-effect-pancake magnetically suspended rigid rotor. The experiment results demonstrated that the method is effective to improve the balancing accuracy for a magnetically suspended rigid rotor system.
Key words:rigid rotor; active magnetic bearing; unbalance vibration; field balancing
中图分类号:TH133.7
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.04.011
通信作者刘刚 男,博士,教授,1970年3月生
收稿日期:2014-08-07修改稿收到日期:2015-02-10
基金项目:国家自然科学基金(61374029)
第一作者 刘超 男,博士生,1987年9月生

