弧形三脚架减振效果及射击精度改善研究
华洪良, 廖振强, 宋 杰, 邱 明, 肖俊波
(南京理工大学 机械工程学院,南京 210094)
弧形三脚架减振效果及射击精度改善研究
华洪良, 廖振强, 宋杰, 邱明, 肖俊波
(南京理工大学 机械工程学院,南京210094)
摘要:为研究一种新型弧形三脚架结构对机枪振动抑制以及射击精度改善情况,基于ADAMS以及相关实验数据建立了准确的机枪系统刚柔耦合动力学模型。在其余条件一致的情况下,对比了不同枪架在射击过程中的膛口动力学响应。根据外弹道理论,以及弹头出膛口扰动,对射击100 m距离弹头散布进行了计算。结果表明:膛口的振动主要体现在高低方向上(y轴),在该方向上膛口位移、速度、射角峰值平均值分别降低了27.8%、25.8%、31.1%左右。弧形三脚架对应的弹头散布圆半径R100,R50分别改善了33.6%、23.2%。弧形三脚架结构可有效改善机枪系统射击精度。
关键词:减振;刚柔耦合动力学;三脚架结构;射击精度;机枪系统
枪架是机枪的重要组成部分,是考核机枪性能的一个重要因素。在支撑重机枪射击过程中,枪架的弹性变形过大是影响机枪振动以及射击精度的主要原因之一。因此,提高枪架结构弯曲刚度减少机枪系统振动,是提高武器射击精度的主要途径之一[1]。文献[2]以某型重机枪三脚架为研究对象,基于网格变形技术并结合Kriging响应面模型以及多目标遗传优化算法对三脚架架腿进行了多目标形状优化,得到了轴向刚度、横向刚度均较高的三角架结构,如图2。相比初始三脚架结构(图1),其特点主要是两个后架腿由原来的直杆变为两弧形杆,具体尺寸参数见文献[2]。

图1 机枪系统初始三脚架结构Fig.1 Initial tripod structure of machine gun system
为验证该弧形三脚架结构在机枪发射过程中对膛口振动抑制效果以及机枪射击精度改善情况,建立机枪系统刚柔耦合动力学模型,获得机枪射击过程膛口动力学响应,便可借助外弹道理论预测其射弹散布[3-4]。
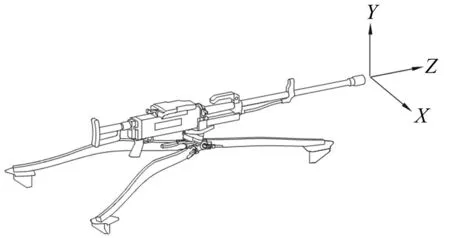
图2 机枪系统弧形三脚架结构Fig.2 Arc tripod structure of machine gun system
1机枪动力学响应
由于机枪发射为一强冲击过程,受到的载荷激励幅值较大,会使得枪管、枪架等细长结构产生较大的弹性变形。基于ADAMS软件,将整枪系统作为刚柔耦合多体系统进行研究,可获得较好的计算精度[4-6]。
1.1模型简化与假设
(1) 刚柔耦合计算前首先对机枪模型简化处理,将无相对运动的部件作为一个运动体,刚度大变形小的部件作为刚体,以减小计算量。发射过程中,刚度小、弹性变形大的零部件作为弹性体考虑。本文将枪管、枪架结构作为弹性体进行建模,具体方法参考文献[7]。
(2) 抽壳、拨弹机构不进行仿真。抽壳阻力、拨弹阻力等按照文献[8]的方式,以外力的形式进行等效加载,直至将枪机框速度调整到与试验曲线[1]吻合,见图3。
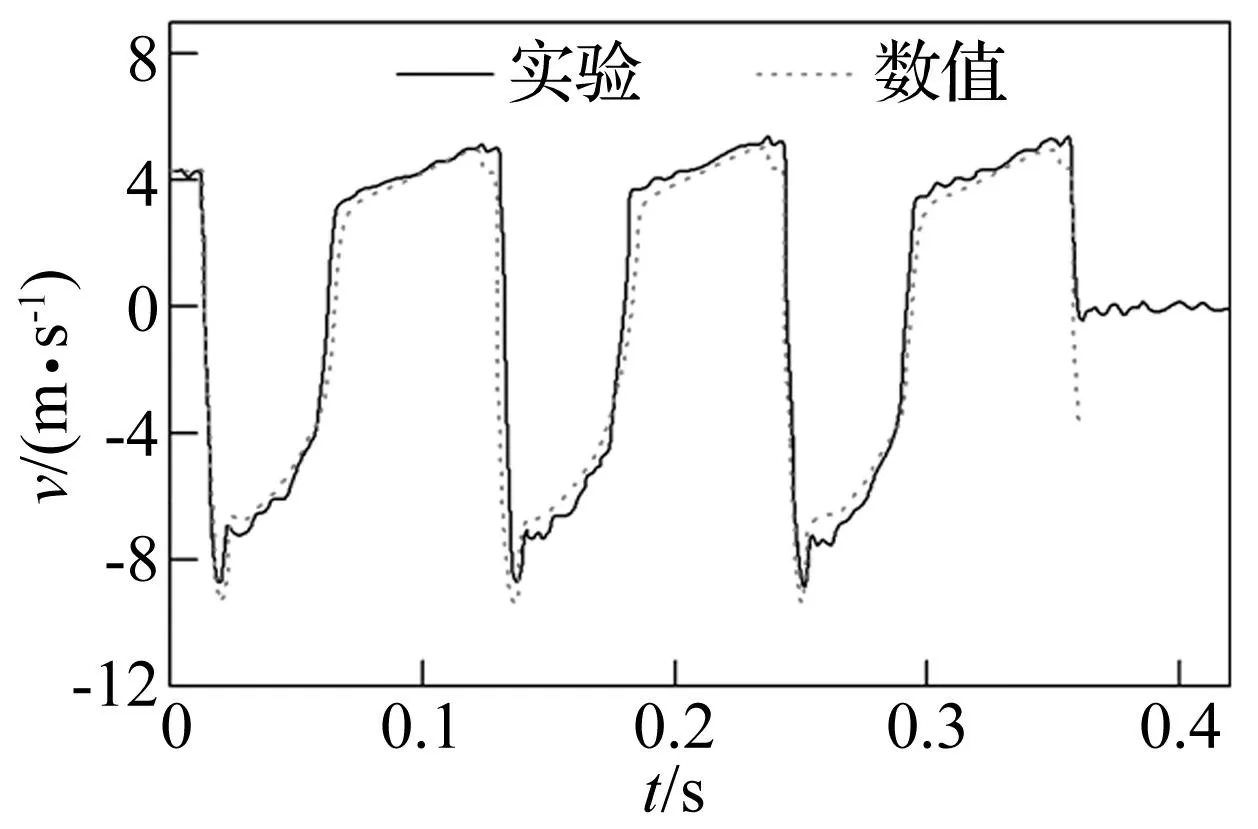
图3 机框速度Fig.3 Blot frame velocity
(3) 发射过程中,枪架与地面接触部分的土壤变形采用三组两两正交的弹簧阻尼器模型进行等效,弹簧刚度、阻尼系数按照文献[9]经验公式有:
(1)
式中:Kh、Kv分别为水平、垂直地面方向等效弹簧刚度;Ch、Cv分别为水平、垂直方向等效阻尼系数;G、ρ分别为土壤弹性模量、密度;r0为驻锄与土壤接触部分在轴向、横向、垂直方向当量接触半径;
土壤弹性模量、密度按照文献[1]进行选取。本文选取的土质为“草地”,土壤密度为1.72 g/cm2,弹性模量为40 kgf/cm2。轴向、横向、垂直方向r0值分别为34.5 mm,50.5 mm,68.3 mm。则相应参数计算如表1。

表1 弹簧与阻尼器参数
1.2载荷确定
机枪射击过程中载荷主要包括:枪膛压力、导气室压力、弹簧力、碰撞力。其中枪膛压力、与导气室压力分别参考文献[10-11]中数学模型,编程求解如图4:P为枪膛压力,Pq为导气室压力。机枪系统中各弹簧参数:复进簧刚度为0.6 N/mm,预压力为65 N;枪管簧刚度为68.5 N/mm,预压力为70 N;制转卡笋簧刚度为2 N/mm,预压力为24 N;肩托缓冲器簧刚度为11 N/mm,预压力为188 N;机头缓冲器簧刚度为5.17 N/mm,预压力为159 N;机框缓冲器簧刚度为540 N/mm。

图4 枪膛压力与导气室压力Fig.4 Bore pressure and gas chamber pressure
1.3动力学模型验证
通过对比机框后坐开始速度、后坐到位速度、机框复进开始速度、复进到位速度便可验证模型的正确性[1]。机框后坐开始速度实验值为9.12 m/s,计算值为9.4 m/s,相对误差为3.07%;机框后坐到位速度实验值为4.09 m/s,计算值为3.9 m/s,相对误差为4.6%;机框复进开始速度实验值为3.93 m/s,计算值为3.75 m/s,相对误差为4.6%;机框复进到位速度实验值为5.2 m/s,计算值为5.24 m/s,相对误差为0.7%。计算得出的机框速度曲线与试验曲线[1]对比如图3,在3.6 s处机框速度实验曲线变为0,而计算曲线仍在反向增加,是因为实验测机框速度采用3连发,本文为了后续比较两种枪架对应的射击精度计算20发,二者其余部分基本吻合,该模型满足分析要求。
1.4动力学响应计算结果及分析
图5(Dx)、图6(Dy)分别为机枪膛口位置沿x,y轴振动幅值;图7(Vx)、图8(Vy)分别为膛口位置沿x,y轴振动速度;图9(Tx)、图10(Ty)分别为膛口位置绕x,y轴振动倾角。可以看出优化得出的弧形三脚架结构在射击过程中膛口高低方向动力学响应Dy、Vy、Tx的峰值平均值分别降低了27.8%、25.8%、31.1%左右,对膛口振动有一定的抑制作用。虽然横向响应Dx、Vx、Ty有所放大,但是相对于高低方向响应十分微小,其影响可不与考虑,后续外弹道计算可说明这一点。


图5 膛口x方向位移Fig.5Muzzledisplacementinx-direction图6 膛口y方向位移Fig.6Muzzledisplacementiny-direction图7 膛口x方向速度Fig.7Muzzlevelocityinx-direction


图8 膛口y方向速度Fig.8Muzzlevelocityiny-direction图9 膛口绕x轴倾角Fig.9Muzzlerotationanglearoundxaxis图10 膛口绕y轴倾角Fig.10Muzzlerotationanglearoundyaxis
2射击精度计算
根据弹头出膛口瞬间膛口扰动便可根据外弹道理论算得机枪射弹散布。根据文献[11],外弹道模型为:
(2)
式中:x,y,S分别为弹头在x,y,z轴方向位移分量;v1、v2、u分别为弹头在x,y,z轴方向速度分量;g为重力加速度;C为弹道系数;H(y)为空气密度函数;G(v)为弹头与空气相对运动特性。
外弹道初始条件为:
(3)
式中:v0为弹头出膛口速度,由内弹道计算得825 m/s;Dx0、Dy0分别为弹头出膛口瞬时x,y方向位移扰动量;Vx0、Vy0分别为弹头出膛口瞬时x,y方向速度扰动量;Tx0、Ty0分别为弹头出膛口瞬时绕x,y轴角度扰动量。Dx0、Dy0、Vx0、Vy0、Tx0、Ty0根据计算得出的弹头出膛口时间分别从图5~10提取得到,限于文章篇幅取十组值列于表2。
图11(左)为外弹道计算得出的初始三脚架结构对应散布圆,图11(右)为弧形三脚架结构对应散布圆。其中,大圆半径为R100,小圆半径为R50。可以看出,机枪射击精度差主要是因为弹头在高低方向散布过大,虽然弹头在水平方向散布略有放大,但相对高低方向散布而言较小,弧形三脚架结构对应的散布精度整体上有所改善。初始三脚架结构对应的R100=0.246 m,R50=0.078 m,对应的实验值[1]分别为0.256 m、0.08 m,则相对误差分别为4.1%、3.1%,可见外弹道计算结果与实验值吻合较好,说明外弹道计算可靠的同时,也表明刚柔耦合数据(外弹道边界条件)可信。弧形三脚架结构对应的R100=0.163 m,R50=0.060 m,相比初始三脚架结构R100、R50分别改善了33.6%、23.2%。
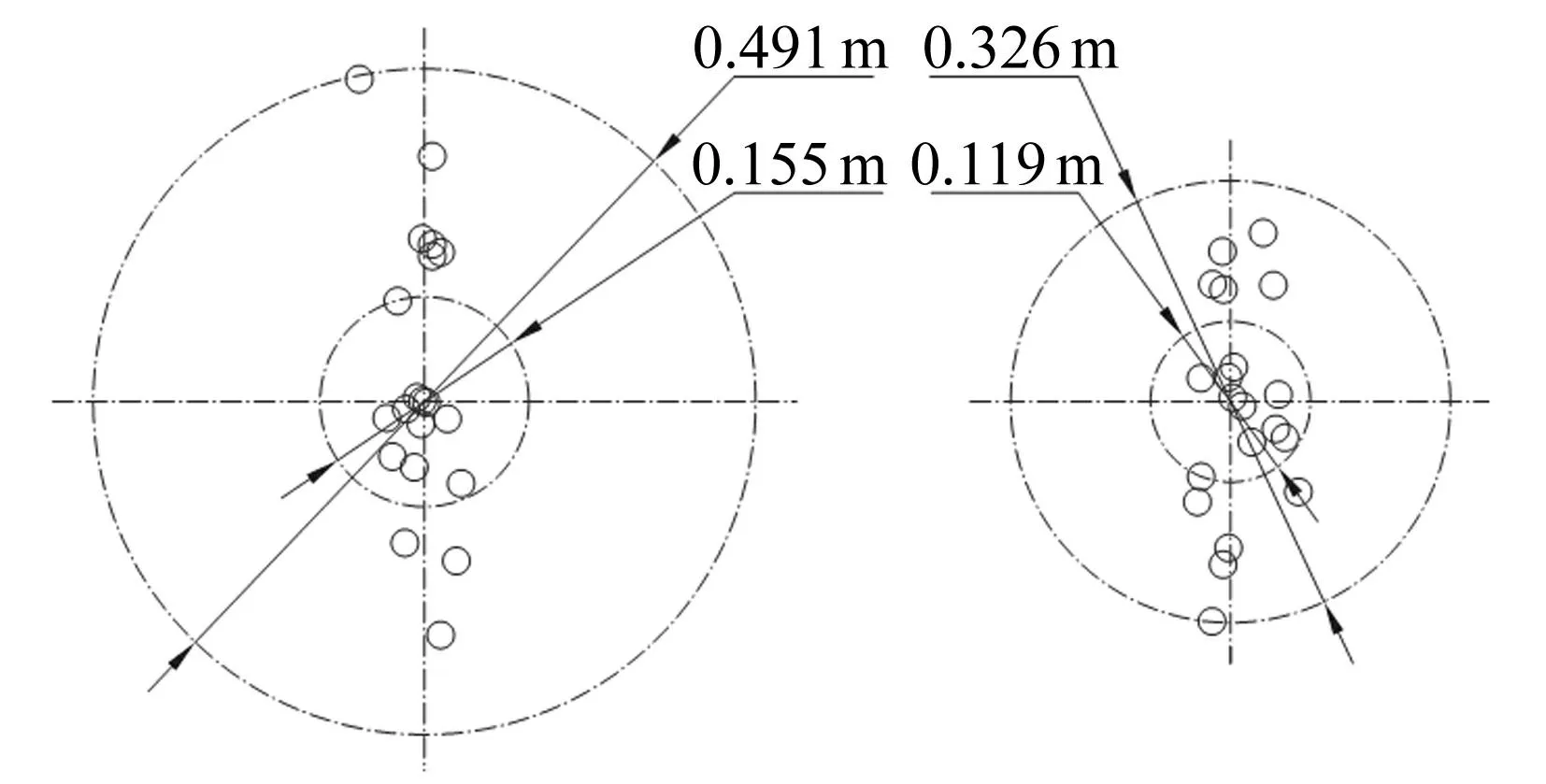
图11 弹头散布比较Fig.11 Comparison of bullets dispersion

弹序Dx0×10-3/mm初始优化Dy0×10-3/mm初始优化Vx0×10-2/(m·s-1)初始优化Vy0×10-1/(m·s-1)初始优化Tx0×10-2/(°)初始优化Ty0×10-1/(°)初始优化10.09-0.091.140.820.750.540.410.210.070.011.110.8620.200.200.730.371.842.842.341.071.950.660.190.0130.290.326.071.662.464.826.160.812.382.503.211.1540.410.430.180.028.201.517.440.752.141.900.810.5550.520.534.582.673.811.935.394.881.901.062.420.8660.630.640.310.190.951.225.803.032.593.730.370.6270.750.753.852.518.423.176.402.470.912.832.160.9780.970.983.001.600.991.906.791.341.440.191.800.47︙︙︙︙︙︙︙︙︙︙︙︙︙192.102.112.311.924.902.105.603.000.810.441.741.42202.212.221.400.942.601.695.971.220.641.320.790.28
3结论
(1) 在其余条件一致的情况下,将枪架作为弹性体考虑,对比了不同枪架在射击过程中的膛口响应。结果表明:膛口的振动主要体现在高低方向上(y轴),在该方向上膛口位移、速度、倾角峰值平均值分别减少了27.8%、25.8%、31.1%左右。弧形三脚架对膛口振动有一定的抑制作用。
(2) 相比初始三脚架,弧形三脚架结构对机枪射击精度有一定改善。外弹道计算表明:弧形三脚架对应的散布圆半径R100,R50分别改善33.6%、23.2%。
参 考 文 献
[ 1 ] 王瑞林. 大口径机枪动力学特性与射击精度研究[D]. 南京:南京理工大学, 2003.
[ 2 ] 华洪良, 廖振强, 邱明,等. 基于网格变形技术的机枪三脚架多目标响应面优化[J]. 振动与冲击,2015,34(16):141-146.
HUA Hong-liang, LIAO Zhen-qiang, QIU Ming, et al.Multi-objective optimization combining response surface model of machine gun tripod based on mesh morphing technology[J]. Journal of Vibration and Shock,2015,34(16):141-146.
[ 3 ] 杨军荣, 杨国来, 陈运生,等. 某车载自动迫击炮的炮口动态仿真[J]. 南京理工大学学报:自然科学版, 2005,29(6):648-652.
YANG Jun-rong, YANG Guo-lai, CHEN Yun-sheng, et al. Dynamic simulation of muzzle motion for a vehicle mounted automatic mortar[J]. Journal of Nanjing University of science and trchnology, 2005, 29(6):648-652.
[ 4 ] 李佳圣, 廖振强, 李洪强,等. 三脚架支承转管机枪射击密集度仿真[J]. 南京理工大学学报:自然科学版, 2013, 37(2):209-214.
LI Jia-sheng, LIAO Zhen-qiang, LI Hong-qiang, et al. Simulation of fire density of gatling gun shooting on light tripod[J]. Journal of Nanjing University of Science and Technology, 2013, 37(2):209-214.
[ 5 ] 徐诚, 王亚平. 火炮与自动武器动力学[M]. 北京:北京理工大学出版社, 2006.
[ 6 ] 陈明, 马吉胜, 王瑞林,等. 基于虚拟样机的机枪结构参数对射击稳定性影响规律研究[J]. 兵工学报, 2008,29(10):1167-1171.
CHEN Ming, MA Ji-sheng, WANG Rui-lin, et al.Research on influence of structure parameters on firing stability of machine gun based on the virtual prototype[J].Acta Armamentarii, 2008, 29(10):1167-1171.
[ 7 ] 李增刚. ADAMS入门详解与实例[M]. 北京:国防工业出版社, 2006.
[ 8 ] 陈锦喜, 王瑞林, 吴海锋,等. 新型机枪枪架及其动态特性分析[J]. 振动与冲击, 2012, 31(8):121-123.
CHEN Jin-xi, WANG Rui-lin, WU Hai-feng, et al. Dynamic characteristics analysis for a new type gun tripod[J]. Journal of Vibration and Shock, 2012, 31(8):121-123.
[ 9 ] 陈明, 马吉胜, 贾长治,等. 基于虚拟样机的某型机枪射击动态性能研究[J]. 计算机仿真,2006,23(8):192-195.
CHEN Ming, MA Ji-sheng, JIA Chang-zhi, et al. Firing dynamic characteristics of a dual-purpose machine gun based on virtual prototype[J]. Computer Simulation,2006,23(8):192-195.
[10] 张小兵. 枪炮内弹道学[M]. 北京:北京理工大学出版社, 2014.
[11] 廖振强, 王涛, 余世海. 武器气体动力学数值计算方法[M]. 北京:国防工业出版社, 2005:221-228.
[12] 王中原, 周卫平. 外弹道设计理论与方法[M]. 北京:科学出版社, 2004.
Vibration reduction performance of an arc tripod structure for firing accuracy improvement
HUAHong-liang,LIAOZhen-qiang,SONGJie,QIUMing,XIAOJun-bo
(School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)
Abstract:In order to study vibration reduction performance of a new type of arc tripod structure for firing accuracy improvement, an accurate rigid-flexible coupled multi-body model of a machine gun system was established based on ADAMS software and related experimental data. The muzzle dynamic responses of the machine gun system with different tripod structures were compared under the same conditions. Based on the exterior ballistic theory and its boundary conditions, the bullet head dispersions were obtained with a firing distance of 100 meters. The results showed that the muzzle vibrations mainly occur in the vertical direction (y axis); in this direction, the peak averages of displacement, velocity and firing angle decrease by about 27.8%, 25.8% and 31.1%, respectively with the new arc tripod structure; the radii of circles with 100% and 50% bullet head scatters by 33.6% and 23.2%, respectively; so the new arc tripod structure can effectively improve the firing accuracy of the machine gun system.
Key words:vibration reduction; rigid-flexible coupled dynamics; tripod structure; firing accuracy; machine gun system
中图分类号:TH212;TH213.3
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.04.010
通信作者廖振强 男,教授,博士生导师,1950年10月生
收稿日期:2014-11-12修改稿收到日期:2015-03-05
基金项目:国家自然科学基金(51375241;51376090)
第一作者 华洪良 男,博士生,1990年10月生

