钢板混凝土复合梁在爆炸荷载作用下的损伤评估研究
田志敏, 章峻豪, 江世永
(1.后勤工程学院 土木工程系,重庆 401311; 2.总参工程兵科研四所,北京 100036)
钢板混凝土复合梁在爆炸荷载作用下的损伤评估研究
田志敏1,2, 章峻豪1, 江世永1
(1.后勤工程学院 土木工程系,重庆401311; 2.总参工程兵科研四所,北京100036)
摘要:为满足钢板混凝土复合梁爆炸损伤评估的实际需要,完成了钢板混凝土复合梁与钢筋混凝土梁承载性能的比较试验,研究了两种梁的承载性能与破坏特点,获得了二者的抗力试验曲线、抗弯变形限值及抗力函数。基于钢板混凝土复合梁的等效单自由度运动方程,采用数值求解方法,得出了评估其在爆炸荷载作用下破坏状态的超压-冲量(P-I)等损伤曲线。研究结果表明:钢板混凝土复合梁的承载力、变形限值、临界超压以及临界冲量比钢筋混凝土梁的都要高,前者的抗爆性能更好。
关键词:钢板混凝土复合梁;变形限值;抗力函数;P-I曲线;临界超压;临界冲量
已有的理论和试验研究表明[1-6],钢板混凝土复合结构具有比普通钢筋混凝土结构更优良的抗爆性能,比之后者,前者不仅抗力要高,而且爆炸破坏后的延性和整体性更好,复合结构的下覆钢板与混凝土中的钢筋骨架形成一体能有效地防止混凝土的爆炸震塌,约束爆炸导致的结构中混凝土碎块的分散。由于其广泛的抗爆应用前景,近20多年来,对钢板混凝土复合结构抗爆性能及其应用开发的研究,已成为防护工程和反恐防爆等领域的研究热点之一,也有许多学者对这种复合结构的抗爆性能从不同侧面进行过卓有成效的研究。在爆炸空气冲击波荷载作用下钢板混凝土复合结构的破坏模式与其材料性能、截面形式、约束条件以及外荷载特征等因素有关。在常规装药近区和接触爆炸作用下,梁主要产生以爆炸成坑和材料破坏为主要特征的局部破坏,而在爆心距较远的常规装药爆炸或核爆炸产生的空气冲击波作用下,梁一般可呈现出整体弯曲破坏、弯剪破坏及剪切破坏等典型形态。由于在实际结构应用中,整体剪切破坏是人们不希望发生并能通过合理设计加以避免的一种破坏形式,因此,目前针对钢板混凝土复合结构的整体抗弯性能研究较多,对其抗剪特性研究较少,对其理论研究居多,而试验研究较少,理论分析结果尚需进一步用系统的试验结果加以验证。总的说来,迄今为止,比之对普通钢筋混凝土结构的研究[7-10],对钢板混凝土复合结构的破坏机制及爆炸损伤评估方法的研究仍是需要不断探求解决的主要问题。
为满足钢板混凝土复合梁的爆炸损伤评估实际需要,作者带领研究小组完成了其与钢筋混凝土梁承载性能的比较试验,研究了其抗力与破坏特性,获得了其抗力函数和承载变形限值,提出了其在爆炸空气冲击波荷载作用下的损伤评估方法,绘制出了便于评估其抗爆炸整体破坏能力的超压-冲量(P-I)等损伤曲线(见图1)。考虑到对于实际结构,其剪切破坏是人们不希望发生并能通过合理设计避免发生的一种破坏形式,本文主要介绍钢板混凝土复合梁的抗弯特性试验结果,研究梁的抗力函数和抗弯变形限值,并针对评估梁抗爆炸空气冲击波整体破坏能力需要,提出了梁在弯曲破坏模式情况下的超压-冲量等损伤评估方法。

图1 P-I等损伤曲线示意图Fig.1 Sketch of Pressure-Impulse isodamage curve
1梁抗爆能力的超压-冲量等损伤评估方法
在爆心距较远的常规装药爆炸或核爆炸产生的空气冲击波作用下,梁的等效单自由度(SDOF)体系的运动方程可表示为:
(1)
式中,y(t)为t时刻梁跨中的挠度,M为梁的质量,R(y)为梁的抗力函数,F(t)为t时刻梁表面的爆炸荷载;KM、KR、KL分别为质量系数、抗力系数和荷载系数,可根据梁两端支承条件、荷载分布形式以及梁的振型确定[12-13]。
假定空气冲击波的超压沿梁的表面均匀分布,且超压时程取为无升压时间的线性衰减形式,则:
(2)
式中,P为构件表面的反射超压峰值,I表示构件表面单位面积的冲量(I=Ptd/2,td为超压持续时间),b和ln分别为梁的宽度和净跨度。
由结构动力学理论可知,等效单自由度梁体系在爆炸荷载作用下的最大动力响应既可用大家所熟知的响应谱曲线描述,也可用P-I等损伤曲线来表示。响应谱表示的是结构最大响应和荷载持时与结构自振周期比值之间的关系,而P-I等损伤曲线表示结构在荷载作用下产生的损伤状态和荷载幅值与冲量组合之间的关系。
图1表示一条典型的P-I曲线,曲线表示的物理含义是,当荷载位于P-I曲线右上方时,梁由该荷载引起的损伤程度要高于这条P-I曲线上的任一荷载引起的损伤程度;反之,当荷载位于P-I曲线左下方时,梁的相应损伤程度较低。
基于等效SDOF理论求解P-I曲线具有简便实用和概念清晰等特点[12-17]。但是,要通过求解方程得出P-I曲线,需要确定梁的抗力函数R(y),并研究提出梁在不同损伤程度时的变形限值。梁的真实抗力函数和对应不同损伤程度时的变形限值需要通过试验才能得出,为此,我们专门完成了钢板混凝土复合梁和钢筋混凝土梁的承载性能比较试验,研究了钢板混凝土复合梁的抗力特性和损伤特征。
2钢板混凝土复合梁和钢筋混凝土梁的承载性能比较试验
2.1试验概况
进行了两组共6根梁的试验,其中钢板混凝土复合梁3根(编号为B1、B2、B3),钢筋混凝土梁3根(编号为A1、A2、A3),支承条件均为简支。试件的尺寸均为150 mm×300 mm×1 800 mm,混凝土为C30级,钢材为Q235钢。钢板的实测屈服强度、极限强度和弹性模量分别为273 MPa、412 MPa和210 GPa;钢筋的实测屈服强度、抗拉强度和弹性模量分别为269 MPa、383 MPa和210 GPa。钢板混凝土复合梁和钢筋混凝土梁的构造和基本参数示于图2。钢板混凝土复合梁的受压区配置2根直径20 mm的钢筋,受拉区钢板规格为1 800 mm(长)×150 mm(宽)×3.5 mm(厚),箍筋直径为8 mm,间距150 mm配置,同时,为了保证钢板与混凝土的协同工作,在梁中配置了剪力连接件(见图2(a));钢筋混凝土梁在拉、压区各配置2根直径为20 mm的钢筋,箍筋直径为8 mm,间距150 mm配置。钢板混凝土复合梁的压区配筋率为1.40%,拉区配筋率为1.17%;钢筋混凝土梁拉、压区配筋率均为1.40%。两种梁的总含钢量相等。
试验在结构多功能试验装置上进行,采用油压千斤顶分级加载,每级荷载为10 kN(变形较小时)或5 kN(变形较大时),一直加载到试件破坏为止。试验装置和试件加载简图示于图3。千斤顶处装有测力计对荷载值进行量测,梁顶钢筋和梁底钢筋(钢板)的应变采用YJB-1A型静态电阻应变仪量测,跨中挠度采用机械式百分表量测。
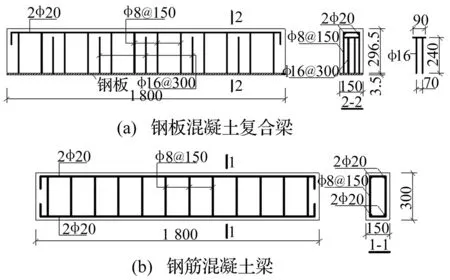
图2 试件配筋图Fig.2 Layout of the reinforcement of two kinds of beams
2.2试验参数量测值和损伤现象
钢板混凝土复合梁、钢筋混凝土梁的试验参数量测值和损伤现象分别列于表1、表2。两种梁的典型损伤照片见图4。
2.3抗力-挠度曲线
图5是钢板混凝土复合梁和钢筋混凝土梁的抗力-挠度曲线。由图5可知,从加载开始, 两种梁的抗力均随着跨中挠度的增加近似呈线性增长,直到受拉钢筋(钢板)屈服,曲线出现明显转折,随着变形的增长,梁的抗力还能继续增加,直至受压区混凝土压碎。但相比钢筋混凝土梁,钢板混凝土梁在混凝土出现压碎以后,随着挠度继续增加,抗力并未出现明显下降,残余承载能力更高,延性更好。
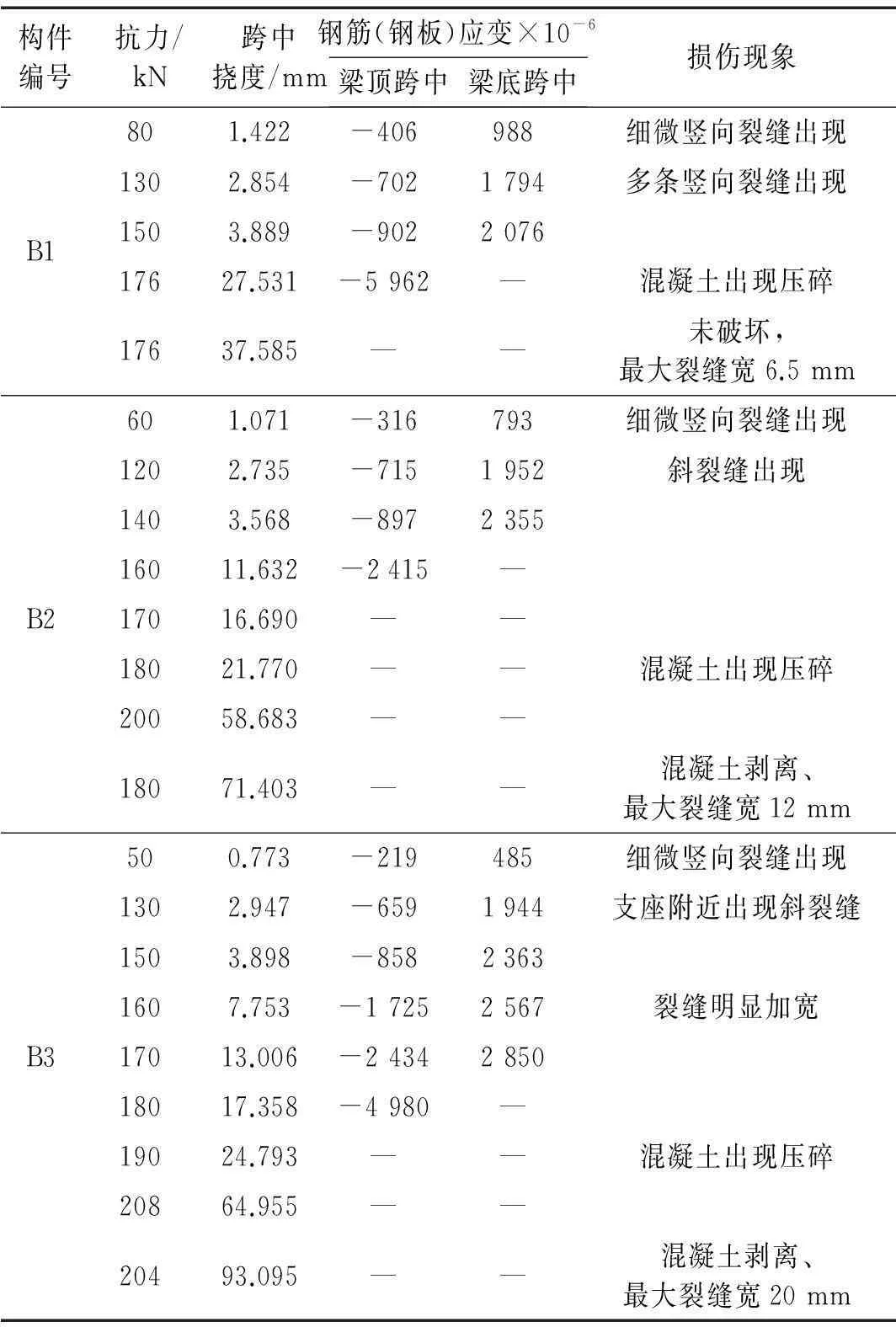
表1 钢板混凝土复合梁的参数量测值和损伤现象
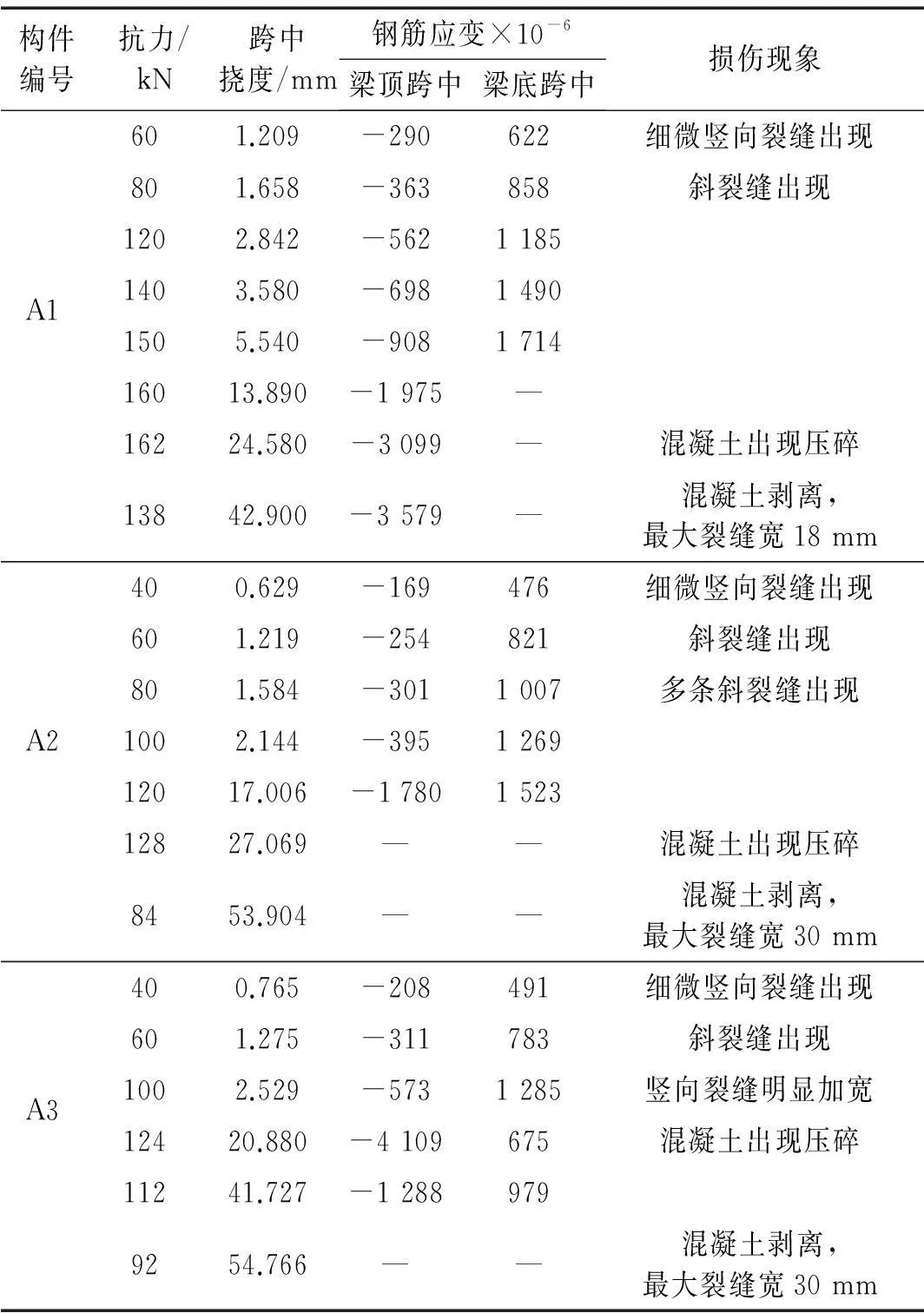
表2 钢筋混凝土梁的参数量测值和损伤现象

图3 加载装置(左)和加载简图(右)Fig.3 Loading device (the left) and the sketch (the right)

图4 典型试件损伤图Fig.4 Pictures of typical damage of specimens

图5 两种梁的抗力-挠度曲线Fig.5 Resistance-deflection curves of the two kinds of beams

图6 钢板混凝土复合梁的切线刚度-挠度曲线Fig.6 Tangent stiffness-deflection of the composite beam
3钢板混凝土复合梁的抗力函数
为了得出钢板混凝土复合梁的抗力函数,首先对图5中抗力-挠度数据进行求导:
(3)
式中,yi和Ri分别表示试验记录的第i个挠度值和抗力值,Kt(yi)表示抗力-挠度数据在挠度为yi处的导数(定义为切线刚度)。
运用式(3)对钢板混凝土复合梁的抗力-挠度数据进行处理后,可得梁的切线刚度随跨中挠度的变化关系,见图6。图中数据可描述为:
Kt(y)=K0[(1-r)exp(-ηy)+r]
(4)
式中,Kt(y)为抗力-挠度曲线在挠度为y处的切线刚度;K0定义为初始切线刚度,K0=Kt(y→0);r定义为切线刚度比,r=Kt(y→yu)/K0,yu为梁破坏时跨中的最大挠度;η定义为刚度衰减速率,η越大,表示切线刚度随着挠度的增长衰减得越快。由图6可知,式(4)与试验数据基本吻合。
对式(4)在区间[0,y]上进行积分,可得:
R(y)=a[1-exp(-ηy)]+by
(5)
式中,a=K0(1-r)/η,b=K0r。
式(5)即本文提出的钢板混凝土复合梁的抗力函数。目前,设计采用的典型抗力函数为分段函数,且采用双线性抗力函数的居多,这种抗力函数除了有理想弹塑性形式[12]外,还有弹塑性增强和弹塑性软化等形式[17],其一般表达式为:
(6)
式中,Ke和Kp分别为构件在弹性阶段和塑性阶段的刚度;yy和Ry分别为屈服点对应的挠度和抗力。

图7 钢板混凝土复合梁的不同抗力函数比较Fig.7 Comparison of different resistance functions for the composite beam
采用抗力-挠度试验数据对式(5)和式(6)进行比较,结果示于图7。由图7可知,当采用式(6)时,需要识别构件的屈服点(yy,Ry)并区分构件的弹性和塑性阶段,当屈服点不明显时这会引起较大误差,相比之下,式(5)避免了人为寻找(yy,Ry),且与试验数据基本吻合。另一方面,采用式(6)时,由于弹性和塑性阶段的抗力表达式不同,因此,体系的运动方程必须按不同阶段分段建立和求解,较为繁琐,而采用式(5)则能有效避免上述问题。
实际上,式(5)对钢筋混凝土梁也适用,如图8所示。图7和图8中式(5)的参数值列于表3。由表3可见,与钢筋混凝土梁(A1、A2、A3)相比,钢板混凝土复合梁(B1、B2、B3)的初始切线刚度(K0)较大,而刚度衰减速率(η)较小,说明钢板混凝土复合梁的刚度较大且刚度随挠度增长衰减得较慢。钢板混凝土复合梁的切线刚度比(r)为正,反映其抗力-挠度曲线呈硬化上升型;而钢筋混凝土梁的r为负,反映其抗力达到峰值以后,抗力-挠度曲线呈软化下降型。总的来看,钢板混凝土复合梁的受力性能较好。
另外,对相关文献中的试验数据进行分析时,发现式(5)对其余梁、柱也具有一定的适用性,如图9所示,试验数据与式(5)基本吻合。

图8 钢筋混凝土梁的不同抗力函数比较Fig.8 Comparison of different resistance functions for reinforced concrete beam
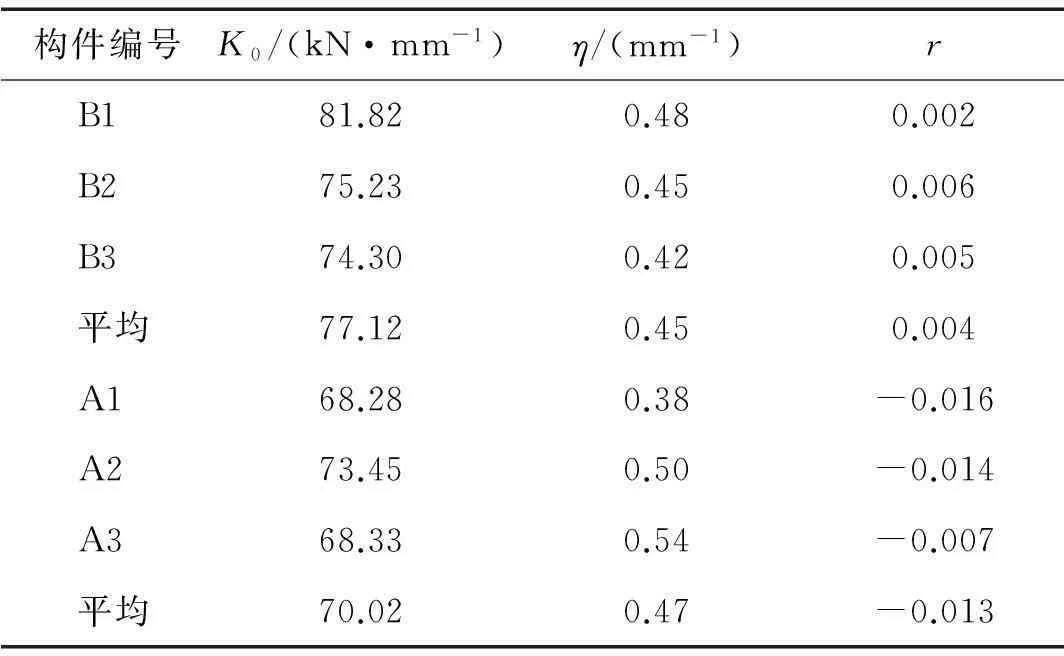
构件编号K0/(kN·mm-1)η/(mm-1)rB181.820.480.002B275.230.450.006B374.300.420.005平均77.120.450.004A168.280.38-0.016A273.450.50-0.014A368.330.54-0.007平均70.020.47-0.013

图9 采用其余文献中的试验数据对式(5)进行验证Fig.9 Validation of equation (5) using test data from other literatures
4钢板混凝土复合梁的变形限值
根据钢板混凝土复合梁在加载试验过程中的参数量测值和损伤特征,及其与损伤程度的对应关系,可确定不同损伤程度之间的变形限值。
4.1损伤程度的划分
参照文献[12-14]中划分损伤程度的方法,构件的损伤程度和相应的损伤特征分别为:
轻度损伤:构件无永久变形,或出现细微裂缝,可继续使用。
中度损伤:受拉钢筋(钢板)屈服,构件产生一定的永久变形,裂缝较多,但修复后仍满足正常使用需求。
重度损伤:构件产生明显的永久变形,混凝土被压碎,难以维修。
失效:混凝土剥离,构件丧失其结构完整性,变形迅速增加,承载力急剧下降。
为了叙述方便,用D1表示轻度损伤和中度损伤的界限(即受拉钢筋(钢板)开始屈服,或抗力-挠度曲线出现明显转折),D2表示中度损伤和重度损伤的界限(即混凝土出现压碎,或受压钢筋开始屈服),D3表示重度损伤和失效的界限(即混凝土开始剥离,或抗力急剧下降)。
4.2变形限值的确定
考虑到采用的变形评价指标应与构件的损伤特征相关联,且容易通过试验和其他分析方法得到,因此采用支座转角和延性比来反映构件变形的大小。发生某一级损伤时对应的支座转角定义为[13]:
(7)
式中,θ为支座转角;ym为梁发生某一级损伤时的跨中挠度;ln为梁的净跨度。
相应地,发生某一级损伤时的延性比定义为:
μ=ym/ye
(8)
式中,ye为构件屈服时的跨中挠度。
由表1和表2的试验数据,结合5.1节中划分损伤程度的方法,可得与D1、D2、D3对应的跨中挠度(ym1(或ye)、ym2和ym3),再利用式(7)和式(8)就可算出与D1、D2、D3对应的界限转角(θ1、θ2和θ3)以及界限延性比(μ1、μ2和μ3),所得结果列于表4。由表4可知,对于钢板混凝土复合梁,μ1=1,θ2=1.87°,θ3=6.24°,相比钢筋混凝土梁(μ1=1,θ2=1.83°,θ3=3.83°),钢板混凝土复合梁各损伤等级之间的变形限值较高,抵抗变形损伤的能力更强。
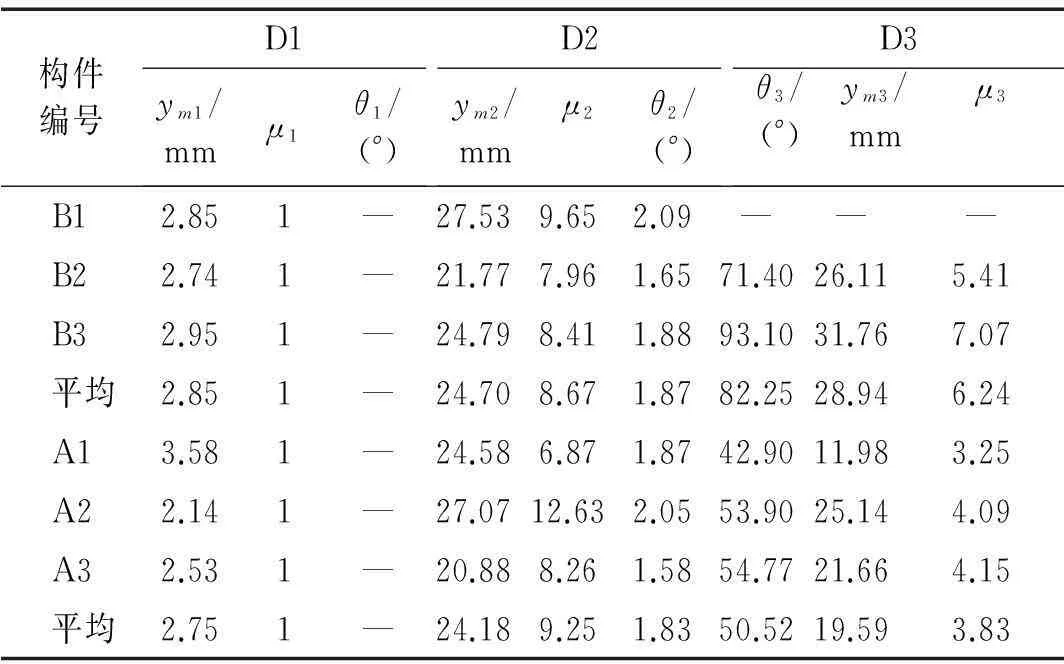
表4 变形限值
5爆炸荷载作用下钢板混凝土复合梁的P-I等损伤曲线
由上述试验分析得出钢板混凝土复合梁的抗力函数和变形限值以后,便可对运动方程(1)进行数值求解,从而得出评估钢板混凝土复合梁抗爆能力的P-I等损伤曲线。求解P-I曲线的步骤为:① 对梁在爆炸荷载作用下的动力响应进行计算,得出其跨中最大挠度,并用式(7)和式(8)计算支座转角和延性比;② 将步骤①得到的变形数值与表4中的变形限值(取平均值)比较,如果二者相差不超过1%,则记录下此次超压和冲量(P, I)组合;③ 重复步骤①和②,得到引起同一变形限值的不同(P, I)组合,将其绘于图中就可以得到该变形限值对应的P-I曲线。
5.1爆炸荷载下梁的动力响应计算
将式(2)和式(5)代入式(1),则等效单自由度体系的运动方程表示为:
(9)
本文采用MATLAB软件的ode45函数对式(9)所示的运动方程进行求解。需要说明的是,由于梁在屈服前后的振型不同,因此KM、KR、KL在梁屈服前后的数值一般不同,但研究表明二者比较接近,且其数值的变化对动力分析结果影响不大[11],为了便于运算,本文取屈服前后的平均值计算,即KM=0.42,KR=1.00,KL=0.57。另外,爆炸荷载下构件的最大抗力比承受静载时有所提高(提高的幅度与材料性质和加载应变率有关),同时不影响构件的塑性性能和延性[18](由变形限值反映),为了简化分析,本文采用构件在准静力试验中的抗力,这也是偏于安全的[5,11]。
5.2钢板混凝土复合梁的P-I曲线
图10给出了钢板混凝土复合梁和钢筋混凝土梁P-I曲线的比较。由图10可知,钢板混凝土复合梁的P-I曲线均位于钢筋混凝土梁的P-I曲线的右上方。由此可见,在钢板混凝土复合梁和钢筋混凝土梁的两条P-I曲线之间的任一荷载值作用下,前者的损伤程度较后者低,即钢板混凝土复合梁的抗爆性能较好。当构件处于D1和D2状态时,两种梁的P-I曲线的位置比较接近,这是因为当爆炸产生的超压和冲量较小时,两种梁的损伤程度均较低,因此反映二者损伤程度的P-I曲线差别不明显。当构件处于D3状态时,两种梁的P-I曲线距离较远,说明当爆炸产生的超压和冲量较大时,钢板混凝土复合梁的抗爆性能明显好于钢筋混凝土梁。
图10中钢板混凝土复合梁和钢筋混凝土梁的超压-冲量数据均可用式(10)描述:
(10)
式中,Pcr为临界超压(对应于P-I曲线的超压渐近线),Icr为临界冲量(对应于P-I曲线的冲量渐近线)[20],m和n是与P-I曲线形态有关的参数。式中的参数取值汇总于表5。

图10 两种梁的P-I曲线Fig.10 P-I curves of the two kinds of beams
由表5可知,构件损伤越严重,其Pcr和Icr的数值越大。当处于同一损伤界限状态时,钢板混凝土复合梁的Pcr和Icr均比钢筋混凝土梁的相应值高(表5括号中的数值表示钢板混凝土复合梁的Pcr和Icr与钢筋混凝土梁相应值的比值)。当处于D1和D2状态时,钢板混凝土复合梁的Pcr比钢筋混凝土梁的高15%~34%,而前者的Icr比后者的高10%~14%;而当构件处于D3状态时,钢板混凝土复合梁的Pcr的提高幅度(45%)与Icr提高幅度(56%)均较大。因此,从两种梁的Pcr和Icr的数值比较也可看出,当爆炸产生的超压和冲量较大时,钢板混凝土复合梁的抗爆性能明显好于钢筋混凝土梁。以下根据等效单自由度理论和能量平衡原理解释这一现象。
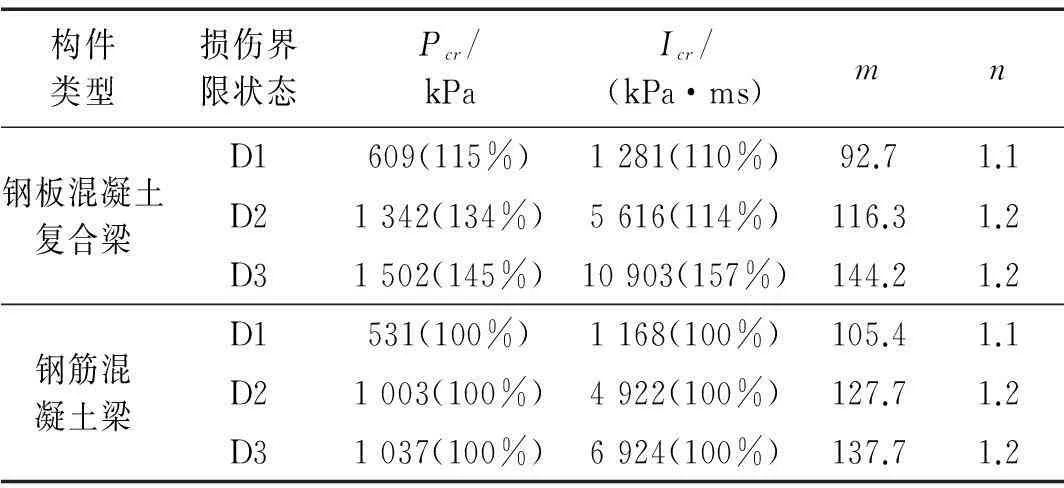
表5 式(10)中的参数取值
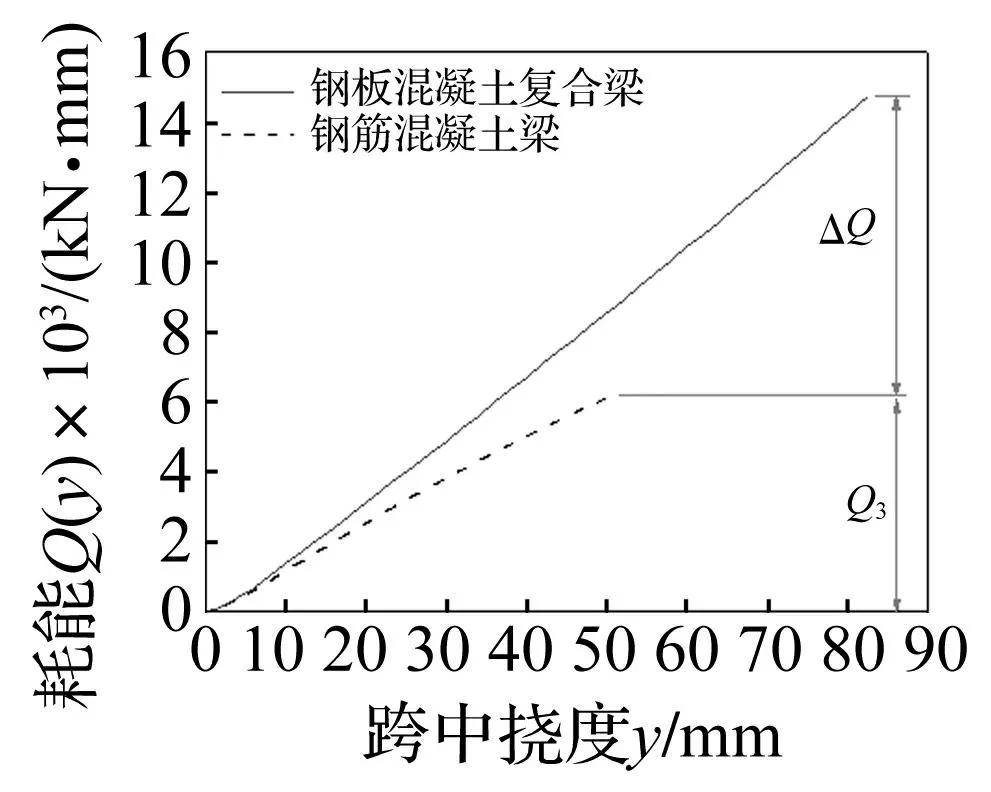
图11 两种梁的耗能-挠度曲线Fig.11 Energy consumption-deflection of the two kinds of beams

KLPcrblnym=Q(ym)
(11)
即:
(12)
由于KLbln为定值,因此:
(13)
即Pcr与耗能-挠度曲线上某一界限挠度ym处的割线斜率成正比。
另一方面,当构件遭受冲量荷载作用时,根据构件的动能与其变形耗能相等可得:
(14)
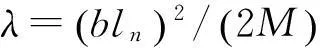
(15)
由于λ为定值,故:
(16)
即Icr与耗能-挠度曲线上某一界限挠度ym处的耗能值的平方根成正比。
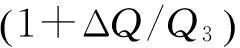
6结论
(1) 钢板混凝土复合梁的切线刚度随挠度的增长呈指数衰减规律,与钢筋混凝土梁相比,钢板混凝土复合梁的刚度较大且其随挠度增长衰减较慢。钢板混凝土复合梁的抗力函数可用式(5)描述。
(2) 与钢筋混凝土梁相比,钢板混凝土复合梁各损伤程度之间的变形限值较高,抵抗变形损伤的能力更强。
(3) 钢板混凝土复合梁的抗爆性能比钢筋混凝土梁更好,前者的临界超压Pcr和临界冲量Icr分别比后者高出15%~45%和10%~57%。
必须指出,本文主要针对简支梁发生弯曲破坏的情况进行了研究,对于梁在其它不同边界条件下发生其它破坏模式时的损伤评估,将在另文中进行研究。
参 考 文 献
[ 1 ] Quinn L T, Kennedy L J, Mays G C. The response of steel/concrete sandwich panels to close-in explosions[C]//Proceeding of the 8th International Symposium on Interaction of the Effects of Munitions with Structures. Mclean, VA, 1997: 631-640.
[ 2 ] Watson A J, Hulton F G, Pope D J. An experimental study of steel plate bonding to concrete slabs under close-in explosions[C]//Mclean Virginia: Proceeding of the 8th International Symposium on Interaction of the Effects of Munitions with Structures. Mclean,VA,1997: 971-979.
[ 3 ] Tian Z, Chen J. Bending resistance of steel plate-reinforced concretebeam[J]. Transactions of Tianjin University, 2006, 12: 210-213.
[ 4 ] 柳锦春, 方秦, 张亚栋, 等. 爆炸荷载作用下内衬钢板的混凝土组合结构的局部效应分析[J]. 兵工学报, 2004, 25(6): 773-776.
LIU Jin-chun, FANG Qin, ZHANG Ya-dong, et al. Analysis of local effects on steel-backed concrete composite structures under blast loading[J].Acta Armamentar, 2004, 25(6): 773-776.
[ 5 ] Smith P D, Hetherington J G. Blast and ballistic loading of structures[M].Oxford, UK: Butterworth Heinemann, 1994.
[ 6 ]Krauthammer T. Modern protective structures [M]. New York, USA: Taylor & Francis Group, 2008.
[ 7 ] Carta G, Stochino F. Theoretical models to predict the flexural failure of reinforced concrete beams under blast loads[J]. Engineering Structures, 2013, 49: 306-315.
[ 8 ] Xu Jue-chun, Wu Cheng-qing, Li Zhong-xian. Analysis of direct shear failure mode for RC slabs under external explosive loading[J]. International Journal of Impact Engineering, 2014, 69: 136-148.
[ 9 ] Ross C A, Schauble C C. Failure of underground hardened structures subjected to blast loading[R]. University of Florida, 1979.
[10] 方秦, 吴平安. 爆炸荷载作用下影响RC梁破坏形态的主要因素分析[J]. 计算力学学报, 2003, 20(1): 39-42.
FANG Qin, WU Ping-an. Main factors affecting failure modes of blast loaded RC beams[J]. Chinese Journal of Computational Mechanics, 2003, 20(1): 39-42.
[11] 王年桥. 防护结构计算原理与设计[M]. 南京: 工程兵工程学院, 1998.
[12] TM5-1300 Structures to resist the effect of accidental explosions[S]. Washington DC: US Department of the Army, Navy and Air force, 1990.
[13] PDC TR-06-01 Rev 1 Methodology manual for the single degree of freedom blast effects design spreadsheets[S]. Washington DC: US Army Corps of Engineers, 2008.
[14] PDC TR-06-08 Rev 1 Single degree of freedom structural response limits for antiterrorism design[S]. Washington DC: US Army Corps of Engineers, 2008.
[15] Dragos J, Wu C. A new general approach to derive normalised pressure impulse curves[J]. International Journal of Impact Engineering, 2013, 62: 1-12.
[16] Dragos J, Wu C. Single-degree-of-freedom approach to incorporate axial load effects on pressure impulse curves for steel columns[J]. Journal of Engineering Mechanics, 2015,141(1):04014098.
[17] Fallah A S, Louca L A. Pressure-impulse diagrams for elastic plastic hardening and softening single degree of freedom models subjected to blast loading[J]. International Journal of Impact Engineering, 2007, 34(4): 823-842.
[18] 清华大学抗震抗爆工程研究室. 钢筋混凝土结构构件在冲击荷载下的性能: 第4集[M]. 北京: 清华大学出版社, 1986.
[19] Zhang Fang-rui, Wu Cheng-qing, Wang Hong-wei, et al. Numerical simulation of concrete filled steel tube columns against BLAST loads[J]. Thin-Walled Structures, 2015, 95: 82-92.
[20] 师燕超. 爆炸荷载作用下钢筋混凝土结构的动态响应行为与损伤破坏机理[D]. 天津: 天津大学, 2009: 73-91.
Damage assessment for steel-concrete composite beams subjected to blast loading
TIANZhi-min1,2,ZHANGJun-hao1,JIANGShi-yong1
(1. Department of Civil Engineering, PLA Logistical Engineering University, Chongqing 401311, China;2. The Fourth Engineer Scientific Research Institute of the Headquarters of the General Staff, Beijing 100036, China)
Abstract:In order to meet the practical needs of damage assessment for steel-concrete composite beams (composite beams) subjected to blast loading, tests for load-bearing capacity of composite beams were conducted and compared with those for reinforced concrete beams. The load-bearing capacities and failure features of the two kinds of beams were studied, their experimental resistance curves, bending deformation limits and resistance functions were obtained. Based on the equivalent single-DOF motion equation of composite beams, the pressure-impulse (P-I) isodamage curves for assessing their damage status were gained by means of the numerical simulation method. The study results showed that the load-bearing capacity, deformation limits, critical overpressure and critical impulse of composite beams are higher than those of reinforced concrete beams, so the formers beams have a better capacity of anti-blast loading.
Key words:steel-concrete composite beam; deformation limits; resistance function; P-I curve; critical overpressure; critical impulse
中图分类号:O383;G449.7
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.04.007
收稿日期:2015-02-27修改稿收到日期:2015-08-29
基金项目:国家自然科学基金资助项目(51278490)
第一作者 田志敏 男,研究员,博士生导师,1962年生
E-mail:zhimintian@163.com

