光纤环十六极对称绕法温度性能的仿真与分析
李绪友,张春梅,刘华兵,凌卫伟,魏延辉
(哈尔滨工程大学 自动化学院,哈尔滨 150001)
光纤环十六极对称绕法温度性能的仿真与分析
李绪友,张春梅,刘华兵,凌卫伟,魏延辉
(哈尔滨工程大学 自动化学院,哈尔滨 150001)
温度性能对光纤陀螺的精度影响至关重要。通过深入研究光纤环的十六极对称绕法,达到了改善光纤陀螺温度性能的目的。在对光纤陀螺由Shupe误差引起的热致旋转速率误差数学模型离散化的基础上,结合ANSYS有限元分析软件建立了精确到匝的光纤环十六极对称绕法有限元模型。根据所建立的光纤环温度分布模型,仿真分析比较了在光纤环四周施加变化的温度激励和分别在径向和轴向施加相同的恒定温度激励下,十六极对称绕法与四极和八极对称绕法绕制的光纤陀螺的温度性能。仿真实验结果显示:由十六极对称绕法绕制的光纤陀螺的热致旋转速率误差要低于四极和八极对称绕法1~2个数量级,这对十六极对称绕法在高精度光纤陀螺中的应用具有重要意义。
光纤环;十六极对称绕法;有限元分析;光纤陀螺
作为新型全固态光学陀螺,与传统的机械式陀螺仪不同,光纤陀螺具有抗冲击、灵敏度高、寿命长、动态范围大、启动时间短等优点,已被广泛应用于航空、航天、航海等领域的惯性导航系统中[1],并正向着高精度方向不断发展[2]。但是当光纤陀螺的工作环境温度发生变化时,光纤环圈中就会产生热致非互易相移,即Shupe误差,而光纤环的缠绕方式直接影响光纤陀螺的温度性能。为了抑制这种与温度相关的非互易相移产生,国内外提出了许多改善光纤环圈温度性能的试验和方法[3-8],其中光纤环的四极对称绕法和八极对称绕法由于对Shupe误差有较好的抑制作用,已经被广泛应用于干涉式光纤陀螺的光纤环圈的绕制过程中[5~7]。但是这两种绕法残余的Shupe误差仍然对高精度干涉式光纤陀螺的温度性能具有重大影响,并且这两种绕制方法只对抑制光纤环径向温度梯度造成的干扰更为有效,而对抑制光纤环轴向温度梯度造成的影响改善情况还不够[9]。
为进一步更有效地抑制光纤陀螺中残余Shupe误差以及径向、轴向热辐射对光纤陀螺温度性能的影响,本文采用十六极对称绕法绕制光纤环。为证明其光纤环圈径向、轴向温度梯度抑制的效果,结合 ANSYS有限元分析软件建立了精确到匝的十六极对称绕法的热致旋转速率误差有限元传热模型。通过对光纤环四周施加变化的温度激励以及分别在径向、轴向施加恒定温度激励,针对十六极对称绕法对Shupe误差的抑制作用进行了仿真实验与定量分析,并分别与四极和八极对称绕法对Shupe误差的抑制作用进行对比。分析结果表明:与四极和八极对称绕法绕制的光纤环圈相比,采用十六极对称绕法绕制的光纤环圈大大提升了其光纤陀螺对Shupe误差的抑制效果。
1 以匝为单位的光纤环圈热致误差数学模型
当光纤环圈中有瞬时环境温度扰动时,就会产生与Sagnac相移无法区分的非互易相移,这种非互易相移将在光纤陀螺中产生较大的偏置误差并限制其应用[12]。在光纤陀螺中由于Shupe误差引起的热致旋转速率误差[5]为
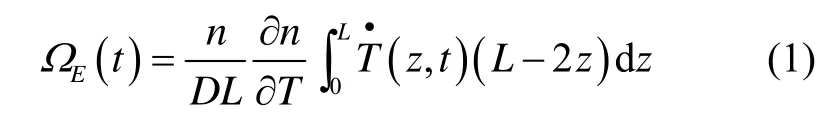
式中:D为光纤环的有效直径(光纤环内外径均值);L为光纤长度;n为光纤的有效折射率;为光纤的温度系数;为该段光纤上z点t时刻的温变速率;(L-2z)为与位置相关的权因子。由式(1)可知,环境温度引起的相位漂移与该段光纤上的温度变化率和与位置相关的权因子成正比,距光纤线圈中点越远,权因子越大。
为了对光纤环圈中产生的Shupe误差进行定量分析,将式(1)离散化。设光纤环共有M层,每层有N匝,这样光纤环就可以等效为由MN匝构成。设第i 匝光纤起点距整个光纤环的起始点(S端)的距离长度为li,且第i匝光纤的长度为dli,则第i匝光纤结束点距整个光纤环的S端的距离长度为li+dli。分别将第i匝光纤的起始点坐标带入式(1),可以得到精确到匝的Shupe误差引起的热致旋转速率误差的离散化表达式:

L-2li-dli是第i匝光纤的位置因子,表示t时刻光纤环Mi层Ni匝位置的温度变化率。通过式(2)可知,光纤环圈中各匝光纤位置因子的差异主要取决于环圈绕制方法的不同,所以不同的光纤环圈绕法产生的旋转角速率误差也不同。
2 十六极对称绕法有限元模型及其对 Shupe误差的抑制作用
2.1 基于ANSYS的十六极对称绕法有限元传热模型
四极对称绕法和八极对称绕法的光纤环的绕制方法和传热模型由于在许多文献中已经被描述过,这里就不再赘述了[5-7]。为保证光纤环中各点相对于光纤环中点的对称性,整段光纤从光纤的中点开始绕制,图1和图2分别为是八极对称绕法和十六极对称绕法的光纤环截面示意图,图中不同颜色图形的圆圈表示分居于光纤环中点两侧的光纤,箭头方向为光纤环的绕制方向,箭头下的数字编号代表光纤环的层数。
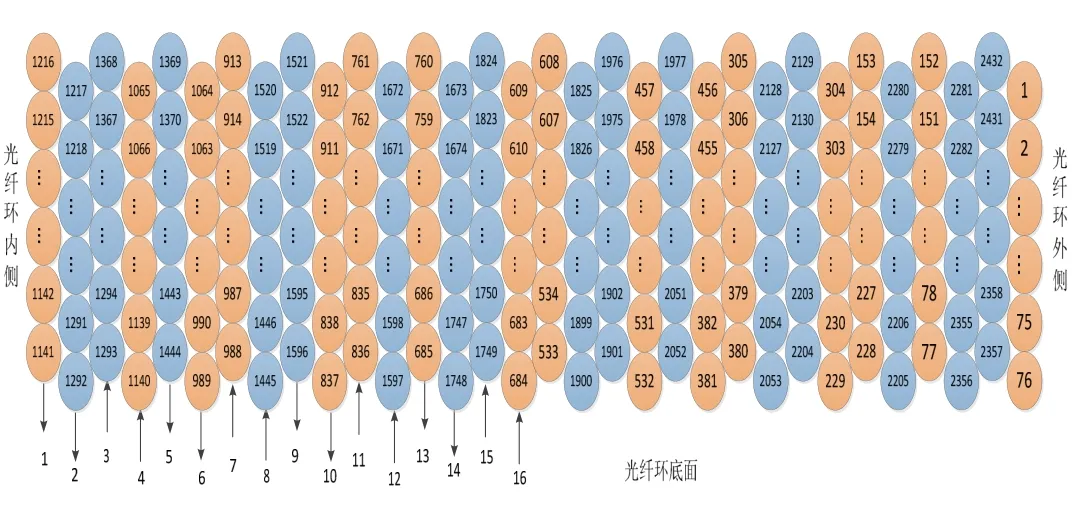
图2 十六极对称绕法精确到匝的光纤环有限元模型截面图Fig.2 Schematic of finite element model of fiber coil, with accuracy to turn, by sixteenpolar winding method
为了能够定量分析十六极对称绕法对Shupe误差的抑制作用,采用ANSYS有限元分析软件对十六极对称绕法绕制的光纤环进行有限元建模。八极和十六极对称绕法精确到匝的光纤环有限元模型如图1和图2所示,其中十六极对称绕法中1~8层的排纤方式与八极对称绕法相同,9~16层的排纤方式与八极对称绕法相反,即将分居光纤中点两侧的光纤交换位置进行绕制,因此9~16层光纤组成一个逆向八极。光纤共绕制32层,每层76匝,共2432匝,圆圈中的数字编号代表各匝光纤的序号,序号的大小代表该匝光纤距该段光纤起点距离的大小。
2.2 利用ANSYS仿真软件建模
采用ANSYS中的二维热单元Quad 4node 55进行建模,根据由保偏光纤构成的光纤环中各组成材料的物理参数,综合考虑计算得到光纤环的参数如表1所示。再通过控制二维模型的边界线划分单元对模型进行网格划分,以确保每匝光纤的截面附近有一个节点。这些节点的位置将代表每匝光纤在光纤环截面中的位置,由光纤环不同的绕法对节点的位置进行相应的定义,再利用每匝光纤的坐标计算其到该段光纤起点的距离,为计算Shupe误差做充分的准备。

表1 光纤环的仿真物理参数Tab.1 Physical parameters of fiber coil in simulation

图3 仿真实验温度载荷曲线Fig.3 Temperature excitation curve of simulation test
温度实验的光纤环会放在温箱中充分与空气接触,所以在ANSYS仿真分析中设定光纤环的四周与空气进行自然对流换热,换热系数为5 W/(K•㎡),初始温度为25 ℃;然后将温度降到-40 ℃,此时保温1 h;再将温度升到60 ℃,再保温1 h。仿真实验的温度载荷曲线如图3所示。第2.3节专门针对在温度变化率为1 ℃/min的情况分别对四极、八极、十六极对称绕法中残余Shupe误差进行比较分析。
2.3 十六极对称绕法对光纤陀螺Shupe误差的抑制作用
当光纤环外温度的温变速率为1 ℃/min时,通过ANSYS仿真解算后,得到各匝光纤温度随时间的分布图和各匝光纤的温度变化率随时间的变化情况分别如图4和图5所示,其中X轴都表示施加温度的时间,Y轴都表示光纤环中光纤的匝数变化。图4和图5的Z轴分别表示光纤环中各匝光纤随时间变化的温度值和温度变化率的分布。

图4 十六极对称绕法光纤环中各匝光纤的温度分布Fig.4 Temperature distribution of each turn in fiber coil by 16-polar symmetrical winding method
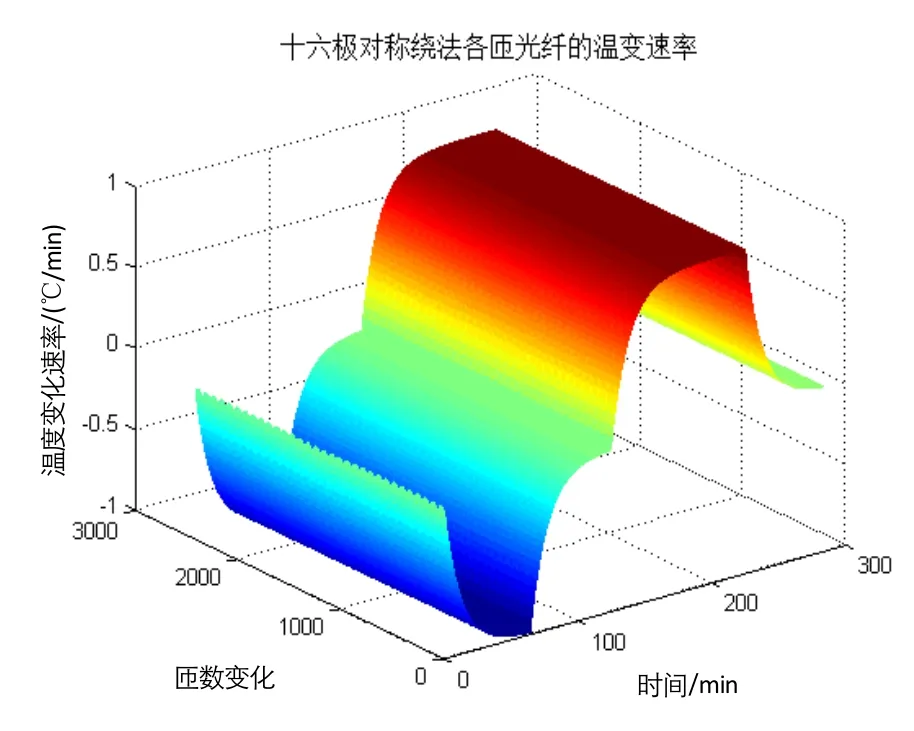
图5 十六极对称绕法光纤环中各匝光纤的温度变化速率Fig.5 Temperature change rate of each turn in fiber coil by 16-polar symmetrical winding method
光纤环内各匝光纤的温度变化率都在1 ℃/min范围内,在保温的时间段内的温度变化率最小几乎接近为零。将十六极对称绕法中的各匝光纤在整段仿真时间内的温度变化率和十六极对称绕法的各匝光纤的位置因子带入离散化的Shupe误数学模型中,得到十六极对称绕法光纤环的热致旋转速率误差如图6所示,并与四极和八极对称绕法光纤环中的热致旋转速率误差进行了比较。
从图6中可以看出,十六极对称绕法光纤环残余Shupe误差比四极八极对称绕法光纤环残余的 Shupe误差要低1个数量级。在温度激励突然降低和升高的过渡时间点,四极和八极对称绕法中的Shupe误差会突然升高或降低,而十六极对称绕法在整个仿真时间段内的残余Shupe误差都趋于平稳,没有较大的起伏,这说明十六极对称绕法光纤环具有更好的温度性能。
光纤环外温度的温度变化率对十六极对称绕法也有一定的影响,通过改变施加温度激励的温度变化率的大小,仿真分析温度变化率分别为 0.5 ℃/min、1 ℃/min、2 ℃/min时光纤环中残余Shupe误差的大小,如图7所示。温度变化率为2 ℃/min时,Shupe误差的极值约为4×10-5(°)/h,而温度变化率为 0.5 ℃/min和1 ℃/min时的Shupe误差均不超过2×10-5(°)/h,且温度变化率为0.5 ℃/min时的Shupe误差在零附近的集中程度明显高于温度变化率为1 ℃/min时的旋转速率误差。所以光纤环外温度激励的温度变化率越小,光纤环的旋转速率误差的变化范围就越小,这对光纤环外部环境的温度控制具有重要的指导意义。

图6 不同绕法光纤环中的残余Shupe误差(a) quadrupolar; (b) octupolar;(c) sixteenpolarFig.6 Residual shupe errors in fiber coil by the three winding methods

图7 不同温变速率下十六极对称绕法光纤环中的旋转速率误差。Fig.7 Rotation rate errors in fiber coil for different temperature change rates by 16-polar method
3 十六极对称绕法对径向温度激励的抑制作用
当光纤陀螺中的散热器件位于光纤环圈内侧时,会相当于热源以恒定的功率沿径向向外辐射热能,这会导致光纤环自内向外各层光纤之间形成一个随时间变化的温度梯度[10],最终会产生比较大的旋转速率误差,给导航造成比较大的角度误差。
为了模拟热源在光纤环内向外辐射热能的情况,在ANSYS仿真中,在光纤环的内侧施加60 ℃的恒定温度激励,时间为1.5 h,施加60 ℃温度激励之前的5 min的温度为0 ℃,施加温度激励后的1 h保持温度为25 ℃,仿真时间为155 min。四极、八极、十六极对称绕法光纤环中产生的旋转速率误差大小如图8所示。
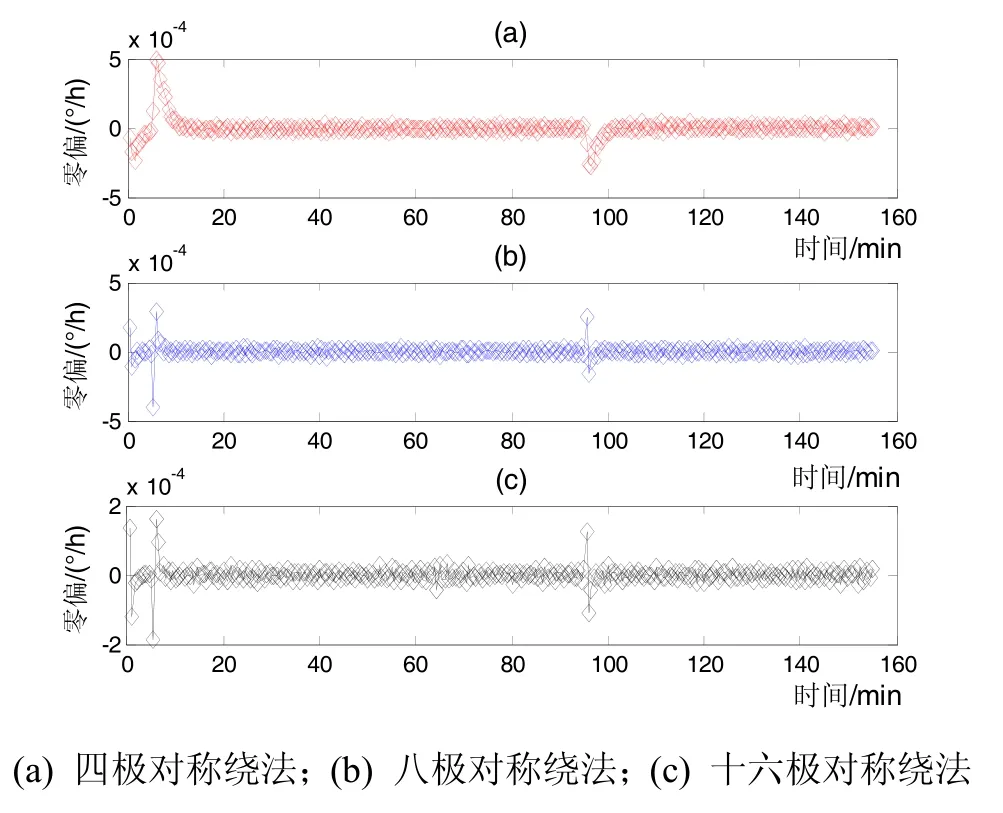
图8 径向光纤环内侧施加温度激励下的热致旋转率误差(a) quadrupolar; (b) octupoalr; (c) sixteenpolarFig.8 Rotation rate error under the temperature excitation imposed in radial inner fiber coil
从图8可以看出,在时间为5 min处,由于加热效应,使光纤陀螺产生一个脉冲速率误差信号,四极对称绕法对此加热效应反应很慢,且产生的峰值旋转速率误差较大约为5×10-4(°)/h,八极对称绕法对5 min处的加热效应的反应速度优于四极对称绕法,且峰值旋转速率误差低于四极对称绕法约为4×10-4(°)/h,而十六极对称绕法在径向温度激励下的峰值旋转速率误差的大小约在2×10-4(°)/h范围内,明显低于其它两种绕法。
同样当光纤环圈外的环境温度扰动和光纤环圈外的散热器件对光纤陀螺的温度性能产生影响时,也会在光纤环中产生较大的温度梯度而形成较大的温度误差。因此同样在ANSYS仿真中,在光纤环外侧施加60 ℃的温度激励,仿真时间和仿真条件和在光纤环内施加温度激励的情况相同。四极、八极、十六极对称绕法光纤环中产生的旋转速率误差大小如图9所示。
从图9中可以看出,在光纤环外侧施加温度激励时,十六极对称绕法下的峰值旋转速率误差比四极对称绕法小2个数量级,比八极对称绕法小1个数量级。同时与图8相比较得到,在施加温度激励的条件不变的情况下,三种绕法的峰值误差信号都大大地增强,但持续时间较短。这是因为热波最先到达最外层光纤,此处的位置因子最大,温度变化速率也大,所以峰值误差信号较光纤环内侧施加温度激励时增强。热波依次向内传播时,热波强度在减弱,同时位置因子也在减小,从而导致旋转速率误差信号较快地趋于零;而当温度激励施加在光纤环内侧时,热波在自内向外经过各层光纤时,强度逐渐减弱的同时位置因子却在逐渐增大,因此旋转速率误差信号要经过较长时间才能趋于零。

图9 径向光纤环外侧施加温度激励的热致旋转速率误差(a) quadrupolar; (b) octupoalr; (c) sixteenpolarFig.9 Rotation rate error under the temperature excitation imposed in radial outer fiber coil.
4 十六极对称绕法对轴向温度激励的抑制作用
理论上讲,四极对称绕法对抑制轴向热辐射引起的旋转速率误差是无效的[9],所以为了证明十六极对称绕法对轴向温度激励的抑制作用,利用ANSYS仿真软件分别在光纤环的上面和底面施加60 ℃的温度激励1.5 h,仿真时间为155 min,前5 min的温度激励是0 ℃,后1 h的温度激励为常温25 ℃。四极、八极、十六极对称绕法下分别在光纤环上面和底面施加温度激励时引起的旋转速率误差如图10和图11所示。
从图10和图11中可以看出,四极对称绕法对温度激励的突然增大产生的脉冲速率误差信号需要一定的时间才能趋于零,而八极和十六极对称绕法对温度的突然升高所产生的误差信号能做出很快的反应。与此同时,无论是在光纤环的底面还是上面施加温度激励,十六极对称绕法下的峰值旋转速率误差都比四极对称绕法小2个数量级,比八极对称绕法小1个数量级。可见十六极对称绕法对抑制光纤环轴向温度激励引起的旋转速率误差具有更好的效果。

图10 轴向光纤环上面施加温度激励的热致旋转速率误差(a) quadrupolar; (b) octupoalr; (c) sixteenpolarFig.10 Rotation rate error under the temperature excitation imposed in tradial inner fiber coil.

图11 轴向光纤环底面施加温度激励的热致旋转速率误差(a) quadrupolar; (b) octupoalr; (c) sixteenpolarFig.11 Rotation rate error under the temperature excitation imposed in radial outer fiber coil
综上所述,与四极对称绕法和八极对称绕法比较,光纤环十六极对称绕法无论在径向和轴向有热辐射时都具有更好的温度性能,这对抑制高精度的光纤陀螺的温度误差是非常有意义的。但是除了上述的与光纤环温度梯度有关的Shupe误差外,还存在着热应力引起的偏置漂移,同样与旋转引起的萨格奈克相移无法区分[11~14],所以后续还需要对热应力引起的漂移误差进行分析。
5 结 论
本文主要针对十六极对称绕法对光纤陀螺Shupe误差的抑制作用。首先对光纤陀螺由Shupe误差引起的热致旋转速率误差的数学模型进行离散化,再结合ANSYS有限元分析建立精确到匝的十六极对称绕法光纤环有限元传热模型。再通过仿真实验定量分析十六极对称绕法对光纤陀螺Shupe误差的抑制作用,并与四极和八极对称绕法进行比较,得出十六极对称绕法残余的Shupe误差比四极和八极对称绕法残余的Shupe误差小1个数量级,同时分析得到外界环境温度变化速率改变越快,对Shupe误差的影响越大。另外,仿真分析单独对光纤环的径向和轴向施加温度激励时,由十六极对称绕法绕制的光纤陀螺具有更好的温度性能,分别在光纤环外侧、上面和底面施加温度激励时,十六极对称绕法的峰值旋转速率误差都比四极对称绕法小2个数量级,比八极对称绕法小1个数量级,可见十六极对称绕法对抑制光纤环径向、轴向温度激励引起的旋转速率误差具有更好的效果。
(References):
[1] Li X Y, HE Z, Zhang C, et a1. Research on modulation stability and compensation method of Y wave guide in fiber optic gyroscope[C]//The Ninth International Conference on Electronic Measurement & Instruments. 2009: 316-321.
[2] Celikel O. Construction and characterization of interferometric fiber optic gyroscope (IFOG) with erbium doped fiber amplifier (EDFA)[J]. Optical and Quantum Electronics, 2007, 39(2): 147-156.
[3] 李绪友, 凌卫伟, 许振龙, 等. 双柱型绕法对干涉式光纤陀螺温度性能的影响[J]. 光学学报, 2016(8): 38-43. Li X, Ling W, Xu Z, et al. Effect of double-cylinder winding on temperature performance of interferometric fiber optic gyroscope[J]. Acta Optica Sinica, 2016(8): 38-43.
[4] Zhang C, Du S, Jin J, et al. Thermal analysis of the effects of thermally induced nonreciprocity in fiber optic gyroscope sensing coils[J]. Optik - International Journal for Light and Electron Optics, 2011, 122(1): 20-23.
[5] 宋凝芳, 关月明, 贾明. 光纤陀螺光纤环 Shupe 误差的多参数影响仿真分析[J]. 北京航空航天大学学报, 2011, 37(5): 569-573. Song N F, Guan Y M, Jia M. Analysis of multi-parameters effect on Shupe error in fiber optic gyroscope fiber coil[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(5): 569-573.
[6] 王玥泽, 陈晓冬, 张桂才, 等. 八极绕法对光纤陀螺温度性能的影响[J]. 中国惯性技术学报, 2012, 20(5): 112-115. Wang Y Z, Chen X D, Zhang G C, et al. Effect of octupole winding on temperature performance of fiber optic gyroscope[J]. Journal of Chinese Inertial Technology, 2012, 20(5): 112-115.
[7] Gao Z. Analysis and simulation for the thermal performance of the octupolar fiber coil[J]. Optical Engineering, 2014, 53(1): 016114-016114.
[8] 刘元元, 杨功流, 尹洪亮. 基于双模型的光纤陀螺温度补偿方法[J]. 中国惯性技术学报, 2015, 23(1): 131-136. Liu Y Y, Yang G L, Yin H L. Temperature compensation for fiber optic gyroscope based on dual models[J]. Journal of Chinese Inertial Technology, 2015, 23(1): 131-136.
[9] 赵勇, 刘军, 张春熹, 等. 光纤陀螺传感线圈及绕法[J].半导体光电, 2002, 23(5): 312-314. Zhao Y, Liu J, Zhang C X, et al. Fiber optic gyroscope sensing coils and their winding method[J]. Semiconductor Optoelectronics, 2002, 23(5): 312-314.
[10] 孟照魁, 崔佳涛, 杜新政, 等. 光纤陀螺系统热建模及仿真[J]. 北京航空航天大学学报, 2007, 33(6): 701-704. Meng Z, Cui J, Du X, et al. Building model and simulation about heat of fiber optical gyroscope[J]. Journal of Beijing University of Aeronautics & Astronautics, 2007, 33(6):701-704.
[11] Chen X, Liu R. Thermal induced nonreciprocity in fiber optic sensors based on Sagnac interferometer[C]//International Symposium on Advanced Optical Manufacturing and Testing Technologies. International Society for Optics and Photonics. 2012: 84181R-84181R-6.
[12] Li X, Ling W, Wei Y, et al. Three-dimensional model of thermal-induced optical phase shifts in rotation sensing[J]. Chinese Optics Letters, 2015, 13(9): 090603-90607.
[13] Ling W, Li X, Xu Z, et al. Thermal effects of fiber sensing coils in different winding pattern considering both thermal gradient and thermal stress[J]. Optics Communications, 2015, 356:290-295.
[14] Zhang Y, Gao Z, Wang G, et al. Modeling of thermalinduced rate error for FOG with temperature ranging from -40°C to 60°C[J]. IEEE Photonics Technology Letters, 2014, 26(1): 18-21.
Simulation and analysis on temperature performance of fiber ring by 16-polar symmetrical winding method
LI Xu-you, ZHANG Chun-mei, LIU Hua-bing, LING Wei-wei, WEI Yan-hui
(College of Automation, Harbin Engineering University, Harbin 150001, China)
A 16-polar symmetrical winding method for fibre ring is studied to improve the FOG temperature performance which is vital to the precision of FOG. Based on the discretized Shupe error mathematical heat transfer model of FOG and by using ANSYS finite element analysis software, a 16-polar finite element model with accuracy to turn is established for fiber coil winding. Then, by applying varied-temperature excitation around the fiber coil and constant-temperature excitation on the radial direction and axial direction of fiber coil respectively, the simulation analysis and comparison are made on temperature performances of FOG winding by quadrupolar, octupolar, and 16-polar symmetrical winding methods respectively according to the fiber coil temperature distribution model. Simulation results show that the thermally induced rotation rate error of FOG wingding by 16-polar symmetrical winding method is 1 to 2 orders of magnitude less than those by quadrupolar and octupolar winding methods, which is important for 16-polar symmetrical winding method’s application in high-accuracy FOGs.
fiber coil; 16-polar symmetrical winding method; finite element analysis; fibre optic gyro
TN253
:A
2016-09-01;
:2016-11-30
科技部国际合作项目(2014DFR10010)
李绪友(1964—),男,教授,博士生导师,主要从事光纤陀螺及光纤陀螺捷联惯导系统的研究。E-mail: lixuyou@hrbeu.edu.cn
1005-6734(2016)06-0780-06
10.13695/j.cnki.12-1222/o3.2016.06.015

