基于UKF的INS/GNSS/CNS组合导航最优数据融合方法

孟 阳，高社生，高兵兵，王 维

（西北工业大学 自动化学院，西安 710072）

基于UKF的INS/GNSS/CNS组合导航最优数据融合方法

孟 阳，高社生，高兵兵，王 维

（西北工业大学 自动化学院，西安 710072）

为了提高INS/GNSS/CNS组合系统的导航精度，提出了一种基于UKF的多传感器最优数据融合方法。该方法具有两层融合结构，第一层中，GNSS和CNS分别通过两个局部UKF滤波器与INS组合，以并行的方式获得INS/GNSS和INS/CNS子系统的局部最优状态估值；第二层中，根据线性最小方差准则推导出一种矩阵加权数据融合算法，对局部状态估值进行融合，获取系统状态的全局最优估计。提出的方法无需采用方差上界技术对局部状态进行去相关处理，克服了联邦卡尔曼滤波(FKF)及其优化形式存在的缺陷。仿真结果表明，相比于FKF，提出方法的导航精度可至少提高36.4%；相比于UKF-FKF，其导航精度也可至少提高21.0%。

INS/GNSS/CNS组合系统；数据融合；联邦卡尔曼滤波；无迹卡尔曼滤波

INS/GNSS/CNS组合导航系统大多采用联邦卡尔曼滤波（Federated Kalman Filter，FKF）综合处理各导航子系统的信息[1-3]。理论上，FKF具有全局最优或近于最优性，同时具有很强的容错能力[4-5]。然而，FKF仅适用于线性系统，当组合导航系统具有非线性特征时，FKF的数据融合精度急剧下降。

无迹卡尔曼滤波（Unscented Kalman Filter，UKF）是一种新兴的非线性滤波算法。与扩展卡尔曼滤波(EKF)相比，UKF滤波精度更高，收敛性更好；与粒子滤波(PF)相比，UKF实现简单，计算量小[6]。因此，学者们将FKF与UKF相结合，用于处理具有非线性特征的INS/GNSS/CNS组合系统中的数据融合问题[7]。但是，由于INS/GNSS和INS/CNS子系统的状态具有相关性，该算法与FKF类似，仍存在两个主要问题[3]：子滤波器采用过程噪声方差的上界而不是其本身进行滤波解算，给全局估计带来一定的保守性；方差上界技术要求各子系统的状态估计误差在初始时刻不相关，这在工程实际中很难实现。

为了避免方差上界技术的使用对数据融合精度的影响，文献[8]提出了一种基于信息矩阵的分散式卡尔曼滤波。然而，由于涉及过多局部与全局状态估值的协方差阵的逆运算，该算法实时性差。在线性最小方差准则下，文献[9]建立了一种适用于高斯系统的多传感器最优数据融合算法，然而该算法并未提供局部状态估值间互协方差矩阵的计算方法。文献[3]提出了一种基于矩阵加权的多传感器数据方法，对文献[9]中提出的算法进行了完善，然而，与文献[8]和[9]所提出的算法类似，该方法仅可用于线性系统中的数据融合，不适用于具有非线性特征的组合导航系统。

本文提出了一种基于 UKF的多传感器最优数据融合算法，以解决具有非线性特征的INS/GNSS/CNS组合系统的信息融合问题。与前人算法不同，该算法具有两层融合结构：在第一层中，GNSS和CNS分别通过两个局部UKF滤波器与INS组合，构成INS/GNSS、INS/CNS子系统，并得到系统状态的局部最优估值；在第二层中，根据线性最小方差准则推导出一种矩阵加权数据融合算法，对局部状态估值进行融合，进而获取系统状态的全局最优估计。该数据融合算法无需采用方差上界技术对局部状态进行去相关处理，克服了FKF及其优化形式存在的缺陷。仿真结果验证了该算法的有效性。

1 INS/GNSS/CNS组合系统数学模型

INS/GNSS/CNS组合导航的基本原理是利用GNSS提供的高精度速度、位置信息和CNS提供的高精度姿态信息，对INS的速度、位置和姿态误差进行修正，最终实现载体连续的高精度导航。

1.1 系统状态方程

将INS的误差方程和惯性测量元件（IMU）的误差方程相结合，建立了INS/GNSS/CNS组合系统的状态方程。

选取东北天地理坐标系（g系）为导航坐标系（n系），记惯性坐标系为i系，地球坐标系为e系，载体坐标系为b系，INS模拟的实际计算平台坐标系为n′系，则以Euler平台误差角表示的INS非线性姿态误差模型和速度误差模型为[10]

式中：φ=（φ,φ,φ）T和δvn=(δv,δv,δv )T分别

式中：vE和vN为载体沿东向和北向的速度；L和h为载体的纬度和高度，δL和δh为载体的纬度误差和高度误差；RM和RN分别为沿地球子午圈和卯酉圈的主曲率半径。

INS的位置误差模型为

通常情况下，陀螺常值漂移 εb和加速度计常值偏置∇b可用随机常数来描述[10]，即

定义系统状态：

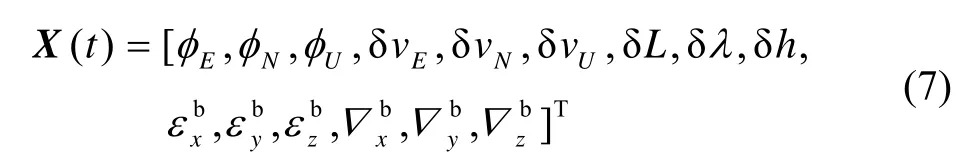
根据所选取的系统状态，结合式(1)～(6)，可建立如下INS/GNSS/CNS组合系统状态方程：

1.2 INS/GNSS子系统量测方程

将INS和GNSS输出的位置与速度的差值作为量测信息，则INS/GNSS子系统的量测方程可表示为

1.3 INS/CNS子系统量测方程

星敏感器输出的赤经、赤纬和旋角经过解算可以得到载体的高精度姿态信息。将INS和CNS输出的姿态的差值作为量测信息，则INS/CNS子系统的量测方程可表示为

式中：H2(k)=[I3×3,03×12]；v2(k)为量测噪声，对应于星敏感器的量测误差。

2 基于UKF的最优数据融合方法

如图1所示，提出的数据融合方法具有两层结构：第一层中，GNSS和CNS分别通过两个局部滤波器与INS组合，以并行的方式获得INS/GNSS和INS/CNS子系统的局部最优状态估值；第二层中，采用矩阵加权数据融合算法对得到的局部状态估值进行融合，以获取INS/GNSS/CNS组合系统的全局最优状态估计。此外，由式(8)可以看到，INS/GNSS/CNS组合系统的状态方程具有非线性特征，因而在局部滤波过程中采用UKF来处理系统状态的估计问题。

图1 基于UKF的多传感器最优数据融合结构图Fig.1 Multi-sensor optimal data fusion based on UKF

2.1 分布式局部状态估计

对式(8)进行离散化处理，可得离散形式的INS/GNSS/CNS组合系统状态方程：

式中：X(k)∈Rn为系统状态；f(·)为非线性函数；w(k)为过程噪声，通常假设为方差Q(k)≥0的零均值高斯白噪声。

INS/GNSS和INS/CNS子系统的量测方程可表示为

式中：Z(k)∈Rmi为第i个局部滤波器的量测量；

iHi(k)为量测矩阵；vi(k)为量测噪声，通常假设为方差Ri(k)＞0的零均值高斯白噪声。这里假定两个子系统的量测噪声互不相关，且均与过程噪声不相关，即

INS/GNSS和INS/CNS子系统利用UKF解算得到各子系统的局部最优状态估值。对于第i(i=1,2)个局部滤波器，UKF算法描述如下：

步骤2 时间更新。经非线性函数f(·)变换后的Sigma点为

状态预测值及其协方差可更新为

步骤3 量测更新。由于INS/GNSS和INS/CNS子系统的量测方程均是线性的，因此量测更新过程与卡尔曼滤波相同：

步骤4 返回步骤1，进行下一时刻滤波解算。

完成两个分布式局部滤波器的并行计算之后，可以得到局部最优状态估值及其误差协方差阵采用2.2节提出的矩阵加权数据融合算法将得到的局部状态估值进行融合，即可获得系统状态的全局最优估计。

2.2 系统状态全局最优估计

步骤2 根据式(23)计算系统状态的全局最优估值：

下面对式(21)～(23)进行推导：

1） 记第i(i=1,2)个局部滤波器的估计误差为

因此，式(21)得证。

2） 借助于式(13)所选择的 Sigma点，采用 UT变换的思想计算可得：

因此，式(22)得证。

其中，wi(i=1,2)为待确定的权值矩阵。

在线性最小方差准则下，系统状态的全局最优估计应满足以下条件：

对式(23)求期望，条件(i)显然满足。

下面讨论如何在条件(ii)下求取系统状态的全局最优估计。

由式(27)和(28)可得：

将式(31)代入其中，有：

3 仿真实验及分析

通过Monte Carlo仿真对提出的基于UKF的最优数据融合方法在INS/GNSS/CNS组合系统中的性能进行了评估，并与FKF和文献[7]提出的基于UKF的FKF（记为UKF-FKF）进行了比较。由于INS/GNSS/CNS组合系统的状态方程具有非线性特征，因此在FKF的局部滤波过程中，需要对系统状态方程进行线性化处理。

假设飞机作机动飞行，包括平飞、爬升、侧滚、转弯、加速、减速、下降等多种飞行状态，其飞行轨迹如图2所示。飞机的初始位置为东经108.997°，北纬34.246°，高度5000 m；初始速度为150 m/s，方向正北；初始姿态为航向角0°、俯仰角0°和横滚角0°，即与载体坐标系平行。采用中等精度的航空惯导，其中：陀螺常值漂移为0.01 (°)/h，白噪声为0.001 (°)/h；加速度计常值偏置为10-4g，白噪声为5×10-5g。GNSS的水平位置误差均方根为3 m，高度误差均方根为5 m，速度误差均方根为0.05 m/s。CNS的姿态误差均方根为5′。INS采样周期为0.05 s，GNSS和CNS的采样周期均为1 s，仿真时间为1000 s。Monte Carlo仿真次数为50次。

图2 飞机飞行轨迹Fig.2 Flight trajectory of the aircraft

对于提出的最优数据融合方法，初始误差协方差阵和过程噪声方差设置为

对于FKF和UKF-FKF，为应用方差上界技术消除两个局部状态间的相关性，将增大为式(37)和(38)所示初始值的两倍。

三种算法中，量测噪声方差设置为

图3～图5为采用FKF、UKF-FKF和提出的数据融合方法计算得到的姿态、速度和位置误差的均方根误差(Root Mean Squared Error，RMSE)曲线。可以看到，FKF的RMSE最大，意味着FKF得到的导航精度最低。这是因为在局部滤波过程中，FKF不但采用了方差上界技术，而且对系统状态方程进行了线性化处理，使得数据融合精度严重降低。UKF-FKF在局部滤波过程中应用UKF进行滤波解算，避免了系统状态方程线性化所导致的截断误差，提高了FKF的精度。然而，相比于提出的数据融合方法，其数据融合精度依然稍低。原因在于，UKF-FKF在局部滤波过程中仍采用了方差上界技术，导致两个局部滤波器始终处于次优的工作模式，因而该算法仅能输出次优的全局估计。相反地，提出的数据融合方法由线性最小方差准则直接推导得到，避免了子滤波器中方差上界技术的使用。因而，无论局部状态估值是否相关，提出的方法都可得到系统状态的全局最优估计。

图3 姿态误差的RMSE曲线Fig.3 RMSE of attitude errors

图4 速度误差的RMSE曲线Fig.4 RMSE of velocity errors

图5 位置误差的RMSE曲线Fig.5 RMSE of position errors

表1给出了三种算法在100～1000 s内得到的姿态误差、速度误差和位置误差的RMSE的均值。由表1的统计结果可知：相比于FKF，提出方法得到的导航误差至少减小了36.4%；即便与UKF-FKF相比，其导航误差也至少减小了21.0%。

仿真结果表明，提出的数据融合方法有效克服了FKF及其优化形式在INS/GNSS/CNS组合系统应用中由于采用方差上界技术而导致融合精度不高的缺陷，显著提高了INS/GNSS/CNS组合系统的导航性能。

表1 导航误差的RMSE均值比较Tab.1 Comparison on mean RMSE of navigation errors

4 结 论

本文提出了一种基于UKF的多传感器最优数据融合方法以解决INS/GNSS/CNS组合系统中的信息融合问题。提出的方法具有两层融合结构：第一层中，GNSS和CNS分别通过两个局部UKF滤波器与INS组合，构成INS/GNSS、INS/CNS子系统，并得到系统状态的局部最优估值；第二层中，根据线性最小方差准则推导出一种矩阵加权数据融合算法，对局部状态估值进行融合，进而获取系统状态的全局最优估计。提出的数据融合方法无需对局部状态估值进行去相关处理，克服了FKF及其优化形式所存在的缺陷。仿真结果表明：相比于FKF，提出方法的导航精度至少提高了36.4%；相比于UKF-FKF，其导航精度也至少提高了21.0%。

（References）：

[1] 周卫东, 王巧云. 基于矢量信息分配的 INS/GNSS/CNS组合导航系统[J]. 哈尔滨工业大学学报, 2015, 47(4): 99-103. Zhou Wei-dong, Wang Qiao-yun. The INS/GNSS/CNS integrated navigation system based on vector information distribution[J]. Journal of Harbin Institute of Technology, 2015, 47(4):99-103.

[2] Hu G G, Gao S S, Zhong Y M, et al. Modified federated Kalman filter for INS/GNSS/CNS integration[C]//Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering, 2016, 230(1): 30-44.

[3] Hu G G, Gao S S, Zhong Y M, et al. Matrix weighted multi-sensor data fusion for INS/GNSS/CNS integration [J]. Proceedings of the Institution of Mechanical Engineers Part g-Journal of Aerospace Engineering, 2016, 230(6): 1011-1026.

[4] Deng H, Liu G B, Chen H M, et al. The application of federated Kalman filtering in SINS/GPS/CNS intergrated navigation system[J]. International Journal of Wireless and Microwave Technologies, 2012, 2(2): 12-19.

[5] Xiong Z, Chen J, Wang R, et al. A new dynamic vector formed information sharing algorithm in federated filter [J]. Aerospace Science and Technology, 2013, 29(1): 37-46.

[6] 赵岩, 高社生, 冯鹏程. 临近空间伪卫星抗风场干扰自主导航[J]. 中国惯性技术学报, 2013, 21(3): 359-364. Zhao Yan, Gao She-sheng, Feng Peng-cheng. Autonomous navigation of near space pseudolite under wind field disturbance[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 359-364.

[7] Huang J, Yan B. Federated filter based on dynamic information allocation with unscented Kalman filter[C]//International Conference on Electrical, Computer Engineering and Electronics. 2015: 911-916.

[8] Chang K C, Zhi T, Saha R K. Performance evaluation of track fusion with information matrix filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(2): 455-466.

[9] Gao S S, Zhong Y M, Shirinzadeh B. Random weighting estimation for fusion of multi-dimensional position data[J]. Information Sciences, 2010, 180(24): 4999-5007.

[10] 孙枫, 唐李军. 基于cubature Kalman filter的INS/GPS组合导航滤波算法[J]. 控制与决策, 2012, 27(7): 1032-1036. Sun Feng, Tang Li-jun. INS/GPS integrated navigation filter algorithm based on cubature Kalman filter[J]. Control and Decision, 2012, 27(7): 1032-1036.

UKF-based optimal data fusion method for integrated INS/GNSS/CNS

MENG Yang, GAO She-sheng, GAO Bing-bing, WANG Wei
(School of Automatics, Northwestern Polytechnical University, Xi’an 710072 , China)

An UKF-based multi-sensor optimal data fusion algorithm is presented to improve the navigation accuracy of integrated INS/GNSS/CNS system. It’s fusion structure has two levels: on the first level, GNSS and CNS are respectively integrated with INS by two local UKFs to obtain the local optimal state estimates in parallel; on the second level, a matrix weighted data fusion algorithm is derived based on the rule of linear minimum variance to fuse the local state estimates for generating the global optimal state estimation. Since the proposed method refrains using the upper bound technique to eliminate the correlation between local states, it overcomes the limitations of the federated Kalman filter (FKF) and its improved forms. Simulation results demonstrate that the navigation accuracy achieved by the proposed method is at least 36.4% higher than that by FKF and 21.0% higher than that by UKF-FKF.

INS/GNSS/CNS integration; data fusion; federated Kalman filter; unscented Kalman filter

V249.3

：A

2016-07-26；

：2016-10-28

国家自然科学基金（61174193）；航天科技创新基金（2014-HT-XGD）资助课题

孟阳（1985—），男，博士研究生，从事组合导航与非线性滤波算法研究。E-mail: horizon131@126.com

联 系 人：高社生（1956—），男，教授，博士生导师，研究方向为导航、制导与控制。E-mail: gshshnpu@163.com

1005-6734(2016)06-0746-06

10.13695/j.cnki.12-1222/o3.2016.06.009