光纤陀螺随机误差的重叠分段Allan分析方法

陈永冰，查 峰，刘 勇

（海军工程大学 导航工程系，武汉 430033）

光纤陀螺随机误差的重叠分段Allan分析方法

陈永冰，查 峰，刘 勇

（海军工程大学 导航工程系，武汉 430033）

针对光纤陀螺随机误差的特点，研究一种有效估计其各种噪声成分系数的Allan方差分析方法。首先，探讨了光纤陀螺随机误差分析中，Allan方差拟合系数为负的原因及利用经典方差方法分析的前提。而后，分析了连续分段的Allan方差分析方法。该方法针对每种噪声的不同相关时间对Allan方差曲线进行连续分段拟合，但方法人为分离了相关时间相近的噪声成分，因此将导致较大拟合误差。为此，提出基于重叠分段的Allan方差分析方法，方法根据Allan方差双对数曲线及噪声特点对相关时间进行混合重叠分段，将相关时间相近的不同噪声化为同一区段，同时为减小相邻区段噪声的方差贡献带来的拟合误差，拟合时将相邻的幂次项纳入拟合模型，提高了拟合精度。光纤陀螺实测数据的分析结果表明，该方法的拟合误差比连续分段Allan方差分析方法减小2/3。

Allan方差；光纤陀螺；随机误差；分段拟合

Allan方差是由美国国家标准局的David Allan为时钟系统中的特征噪声和稳定性分析而提出的时域分析方法，其主要特点是能非常容易地对各种类型的误差源和整个噪声统计特性进行辨识[1-2]。一般认为，光学陀螺随机误差主要包括量化噪声、角度随机游走、零偏不稳定性、角速率随机游走、速率斜坡和正弦分量[3-4]。对于这些随机误差，常规的分析方法（如计算样本均值和方差）并不能揭示出潜在的误差源。虽然自相关函数和功率谱密度函数能够分别从时域和频域描述随机误差的统计特性，但很难分离出这些随机误差。因此，Allan方差分析方法广泛应用于光纤陀螺的随机误差分析中。此外，总方差、#1理论方差也经常应用于系统长时间频率稳定性分析问题中[5-6]。但总方差的数据延伸使其不能真实反映被测系统的性能。利用#1理论方差分析对光纤陀螺分析时，除角度随机游走外，其他噪声项标准差相对于Allan方差存在偏差。因此，Allan方差成为IEEE推荐的陀螺噪声过程特性分析方法。

Tehrani M第一次将Allan方差应用到激光陀螺的随机噪声分析中[7]，随后得到广泛应用。在Allan方差分析中，由于噪声特点、拟合模型等因素的影响，导致其系数拟合误差较大。文献[8]提出采用分段 Allan方差的方法进行光纤陀螺误差分析。同时，张梅[9-10]在激光陀螺的随机噪声分析中认为 Allan方差各噪声项的功率谱不合理而导致拟合系数为负，并基于噪声为阻尼振荡的假设，提出利用经典方差进行激光陀螺的误差分析，并通过大量实验验证了方法的有效性。该方法的前提是陀螺噪声中不快不慢类噪声可以忽略。试验发现，与激光陀螺不同，光纤陀螺的噪声输出中含有低频振荡成分，这正是基于阻尼振荡理论中的不快不慢类噪声项，因此文献的方法难以实现对光纤陀螺的随即噪声分析。此外，在实际光纤陀螺噪声分析中，文献连续分段方法难以准确找到每一噪声成分的频率分界点，甚至在某特定的τ域内相关时间相近的两种噪声对 Allan方差均有贡献，对其进行连续分段拟合可能产生较大误差。

为此，本文提出一种基于混合重叠分段的光纤陀螺噪声分析方法。该方法根据 Allan方差双对数曲线及噪声相关时间特点对τ域进行重叠混合分段，根据τ域内的噪声成分和特点，将相关时间相近的不同噪声化为同一区段，同时为减小相邻区段噪声的方差贡献带来的拟合误差，拟合时将相邻频段内τ的幂次项纳入拟合模型。实验室条件下的光纤陀螺测试和数据分析表明，该方法能够有效估计出各噪声成分及其系数，可为光纤陀螺的性能评价及信号处理提供参考。

1 光纤陀螺的Allan方差分析及局限

1.1 Allan方差定义及分析过程

现以光纤陀螺的角速率输出为采样，阐述 Allan方差分析过程。设光纤陀螺的输出角速率采样间隔为0τ，采样长度为 N。将采集的 N个数据分成 K组（K=N/M），每组包含 M(M≤(N-1)/2)个采样数据，每一组数据的时间长度为称为相关时间。对每一组数据求平均值，记为：

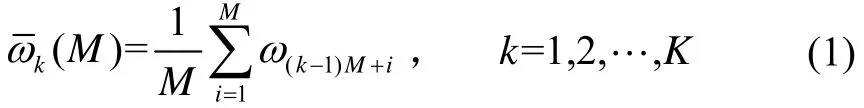
Allan方差定义为：

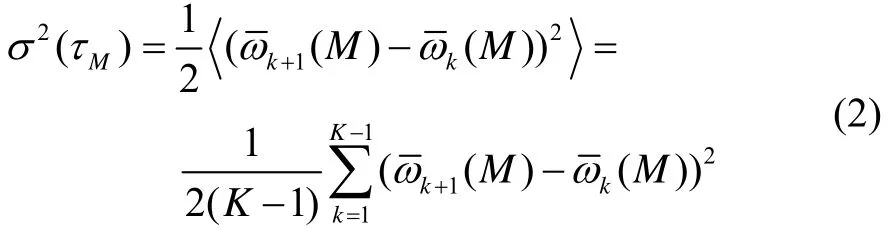
在实际陀螺测试中，数据长度和分组数决定了Allan方差的估计精度[2]。

根据Allan方差的定义，基于陀螺随机过程为平稳过程的假设，可推导出Allan方差与原始测量数据中噪声项的双边功率谱密度存在以下关系：

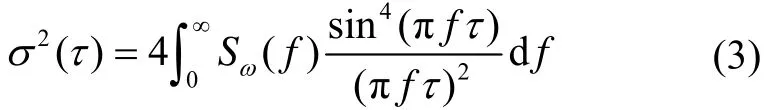
根据各噪声项的功率谱密度，光纤陀螺的量化噪声（Q）、角度随机游走（N）、零偏不稳定性（B）、角速率随机游走（K）、速率斜坡（R）、马尔科夫噪声（M）和正弦噪声（S）的Allan方差分别为：

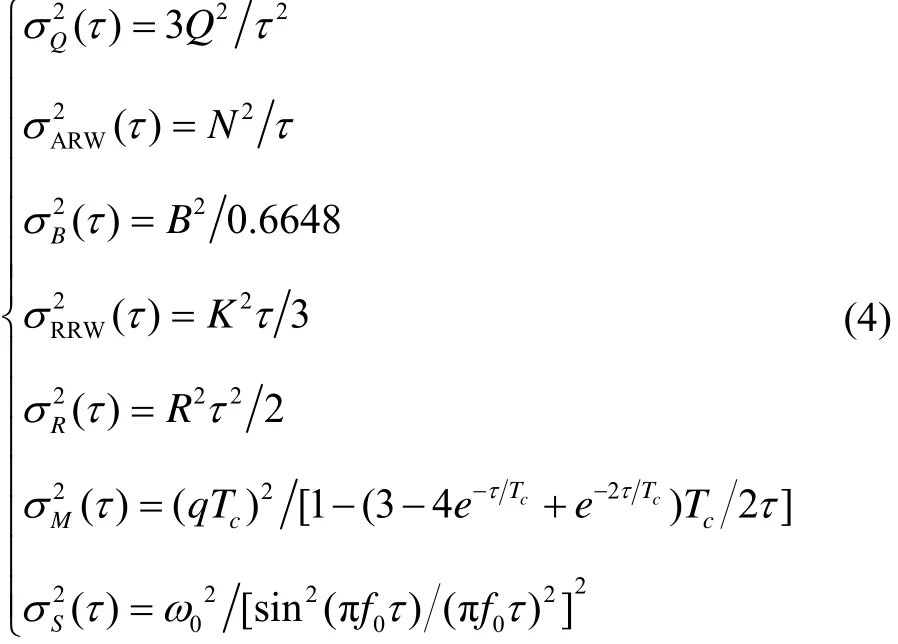
由于各噪声的相关时间不同，不同的噪声项出现在不同的τ域上。在假设各噪声源统计独立情况下，常规文献认为，由于马尔科夫噪声（M）和正弦噪声(S)的影响较小且不易观察，在实际分析中忽略，因此Allan方差的拟合模型可以表示为：

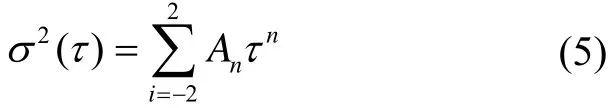
对陀螺输出的Allan方差双对数曲线进行拟合即可求出各多项式系数，根据式(5)，即可求得各噪声系数。由于方差较小，为了提高实际拟合精度，一般对Allan标准差进行拟合。

1.2 Allan方差分析的局限

Allan方差分析方法的突出优点是能容易地对各种类型的误差源和整个噪声统计特性进行细致的表征与辨识。但实际陀螺测试和误差分析中，由于存在许多非确定性误差的影响，其结果通常难以与实际情况相符。

首先，对实验室的2只光纤陀螺进行了测试，将光纤陀螺固定在调平的转台上，采集其输出数据，数据采样间隔1 s。为剔除温度变化引起的陀螺漂移对光纤陀螺噪声分析的影响，数据分析时截取温度稳定后的陀螺输出数据。为便于比较分析不同特征时间的噪声的精度和重复性，分别进行了 20组不同时间的测试试验（其中10组为短时长测试，测试时间为6 h，10组为长时长测试，测试时间约为12 h）。图1为2只陀螺在长时间测试中的典型输出曲线。（1 min平滑结果，为最大程度利用数据长度，未对采集数据截断取整小时处理）。

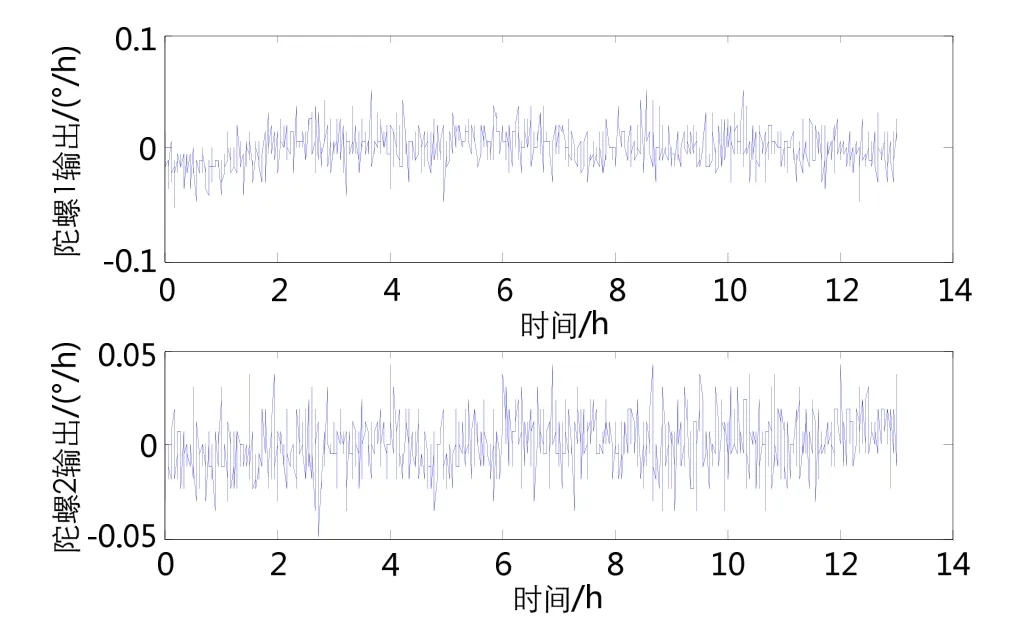
图1 光纤陀螺输出数据Fig.1 FOG’s Output

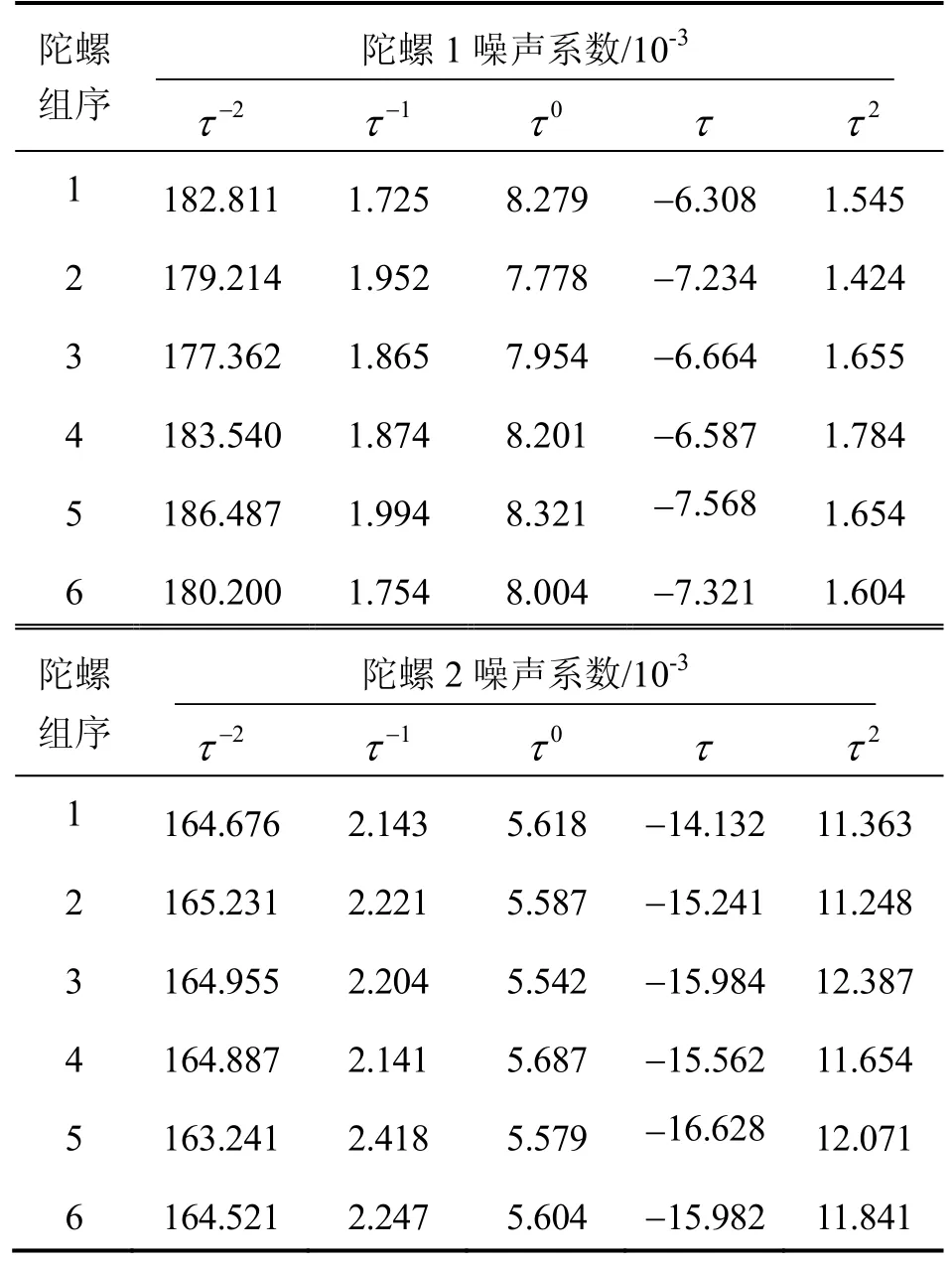
表1 短时测试数据的Allan方差分析结果Tab.1 Results of Allan variance analysis for normal-time test data

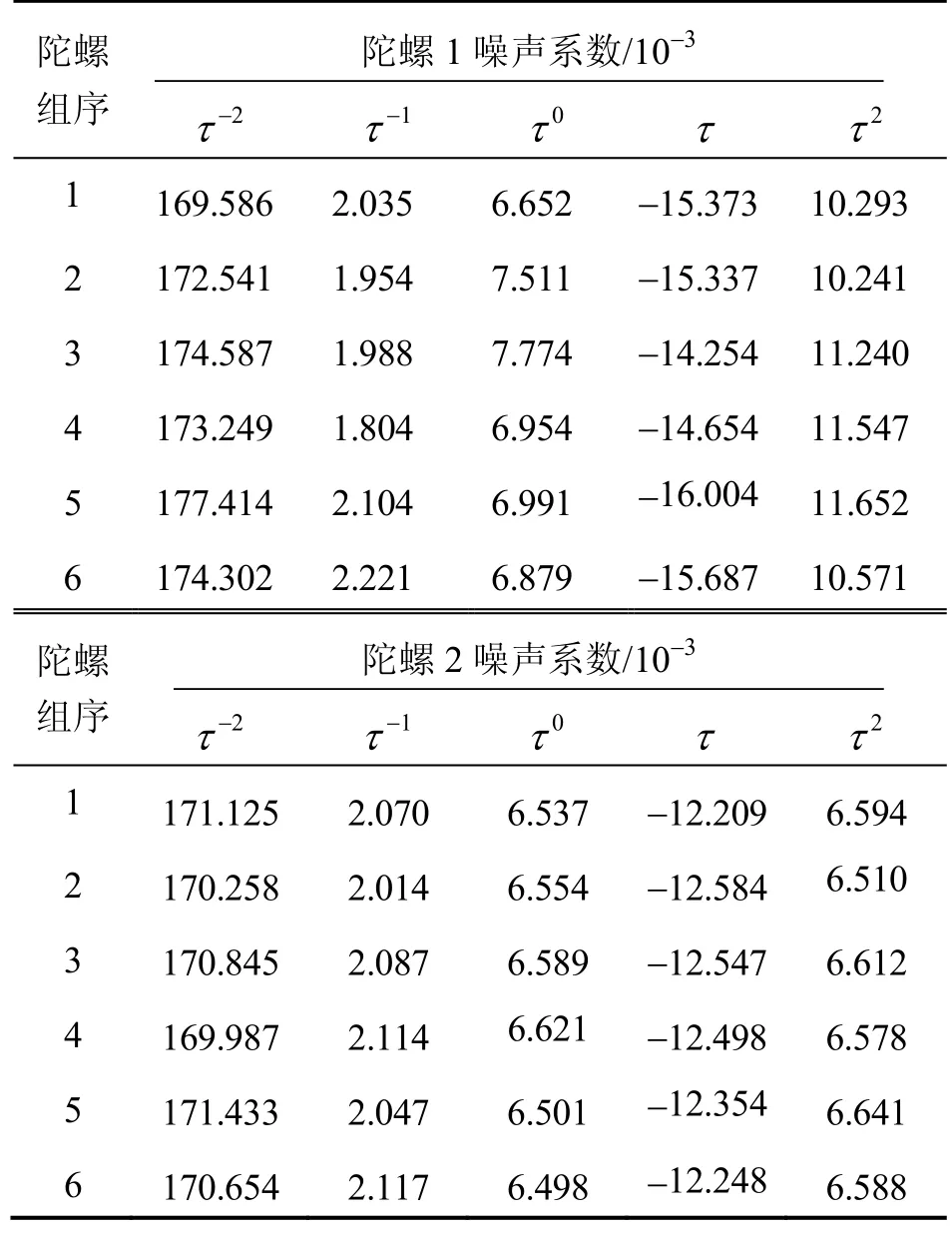
表2 长时测试数据的Allan方差分析结果Tab.2 Results of Allan variance analysis for long-term test data

根据Allan方差的分析方法及过程，分别对2只光纤陀螺的10组短时和10组长时测试数据进行了Allan方差噪声分析，短时数据分析时相关时间取3 000 s，长时数据分析时相关时间取为6 000 s。短时和长时测试数据的Allan方差分析结果分别如表1和表2所示（限于篇幅，仅在表中给出其中6组数据的分析结果）。

对比表1和表2可以看出，在短时间测试和长时间测试两种测试条件下，陀螺1和陀螺2的前三项噪声相对稳定，噪声系数变化不大，这表明量化噪声、角度随机游走、零偏不稳定性这三项噪声具有较短的相关时间，经过 6 h的测试能较好的拟合出其系数。而速率游走和速率斜坡噪声系数在短时测试和长时测试数据的分析中，系数差别较大，因为这两类噪声具有较长的相关时间，短时间测试不能准确估计出其噪声系数。若要估计这两类噪声系数，需增加测试时间，使两类噪声系数逐渐趋于稳定。但同时，速率游走系数出现了负值，这显然与实际不符。为清楚显示，分别取2只陀螺的其中1组长时间测试数据的Allan方差及拟合结果，如图2和图3所示。从图中可以看出，拟合曲线与Allan方差曲线存在较大拟合误差。Allan方差拟合系数与实际不符的主要原因在于，在进行光纤陀螺随机噪声分析时，忽略了马尔科夫噪声和正弦噪声等其它类型噪声影响，而此类型噪声的 Allan方差表现出相关时间的不同幂次关系，拟合过程存在较大误差。因此，连续 Allan方差分析方法难以准确估计出其各噪声项系数。

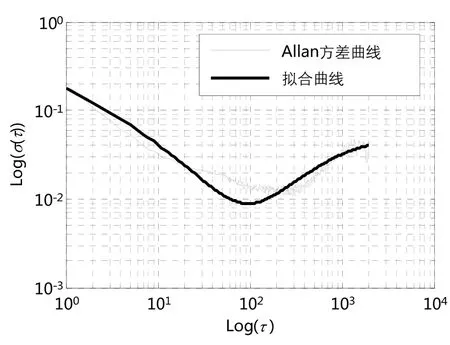
图2 陀螺1 长时间测试数据的Allan方差拟合曲线Fig.2 Allan variance fitting curve of FOG 1 for long-term test data

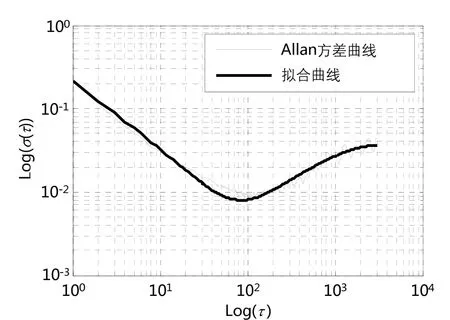
图3 陀螺2长时间测试数据的Allan方差拟合曲线Fig.3 Allan variance fitting curve of FOG 2 for long-term test data

2 基于阻尼振荡假设的经典方差分析及前提

2.1 外 推

文献[9-10]在进行激光陀螺随机噪声分析时，也遇到了相关系数拟合为负值的问题，为有效进行激光陀螺的噪声分析，文献[9-10]基于高伯龙院士[11]提出的陀螺噪声信号为阻尼振荡的假设，利用其阻尼振荡的弛豫时间不同将噪声分为快漂，慢漂和不快不慢项，在进行了大量的试验的基础上提出利用经典方差进行不同陀螺噪声系数拟合的方法。

文献[9-10]指出，假设除量化噪声外，陀螺噪声符合阻尼振荡形式，可将陀螺噪声的功率谱表示为阻尼振荡功率谱与量化噪声的功率谱之和。根据经典方差与频率表达式的关系得到陀螺噪声的标准方差可以表示为：

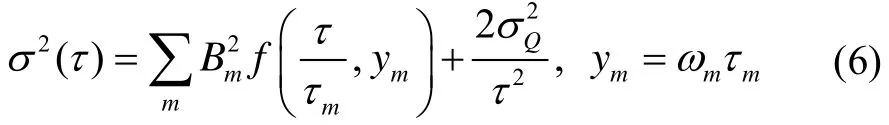
式中：

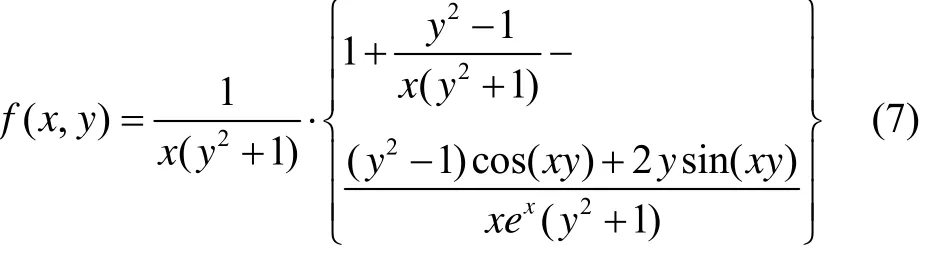
文献[9-10]根据采样周期与弛豫时间的大小，将噪声分为慢漂、快漂、不快不慢项3类。综合上述噪声特点，对进行相应简化，得经典方差为：

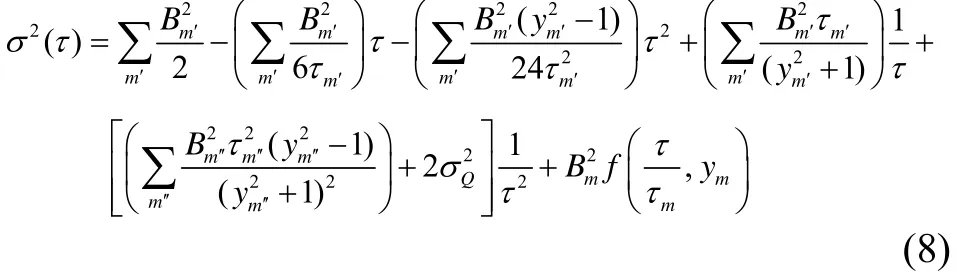
式中：下标m′、m′′和m的分别表示慢漂、快漂和不快不慢项对方差的贡献。将式(8)中τ的系数写成a1、，化为：

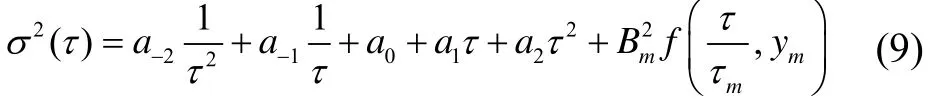
由上式可以看出，在经典方差中，慢漂类噪声对于陀螺的方差的影响表现为，快漂类的噪声的影响主要表现为而不快不慢项的影响形式较为复杂。文献[9-10]认为激光陀螺的不快不慢类噪声较小，忽略式(8)最后一项后得到经典方差各系数取值的结论：a-1≥0，a0≥0，a1≤0，a-2和a2不确定。

因此，通过对测试数据的经典方差拟合，可以求得其幂次项系数。但为保证足够的拟合精度，数据长度一般大于为此对2只陀螺的10组长时间测试数据进行了经典方差分析，10组数据拟合的噪声系数的均值和标准差如表3所示。

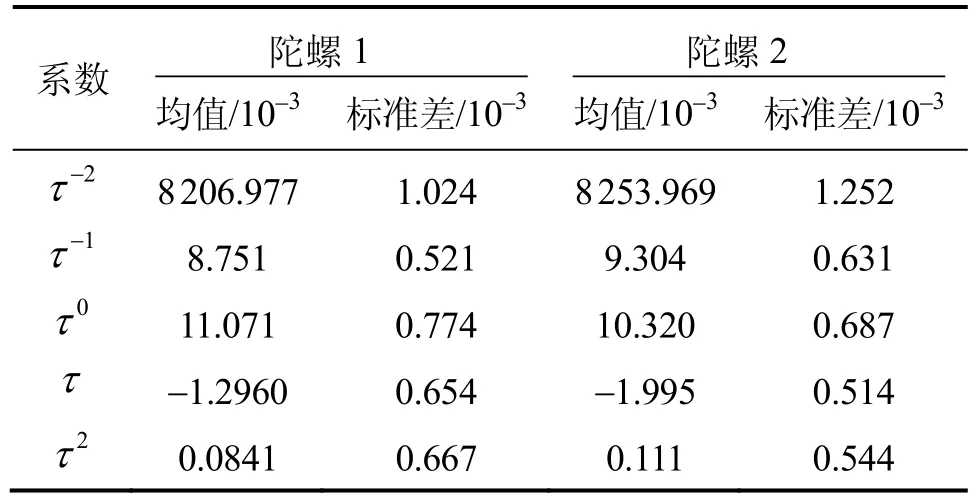
表3 经典方差分析结果Tab.3 Result of traditional variance analysis

从表3可以看出，经典方差拟合的系数符号符合文献[9-10]结论。但是该系数与Allan方差分析的系数差别较大，主要是因为两者划分的噪声类型不一致。经典方差拟合按照噪声的弛豫时间将噪声分为快漂、慢漂和不快不慢项三类，其幂次项系数是不同噪声综合作用的结果，其大小并不能真正揭示各噪声成分的大小。另外，上述经典方差拟合系数取值的结论成立的前提为陀螺噪声中不快不慢类噪声较小，可以将其忽略。实际上，在某些光纤陀螺中存在不快不慢类噪声成分，且不能忽略，若按文献[9-10]的拟合模型进行拟合导致其拟合系数取值结论与文献不符。图4为某型光纤陀螺的输出噪声[12]，利用经典方差拟合系数为

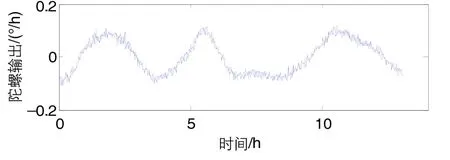
图4 光纤陀螺随机噪声输出Fig.4 Output of FOG random noise

由此可见基于阻尼振荡假设的经典方差分析，其拟合系数是不同噪声成分作用结果，难以揭示各噪声成分的大小。同时，该分析方法的前提为陀螺噪声中不快不慢类噪声可以忽略，某些光纤陀螺实际输出特性不能满足该前提。

3 基于混合分段的Allan方差分析

3.1 连续分段Allan方差分析

针对本文研究的光纤陀螺，Allan方差传统拟合模型存在较大误差，其噪声特点又不满足基于阻尼振荡假设的经典方差分析的前提，因此利用两种方法难以准确衡量陀螺性能。

文献[8]提出利用分段Allan方差的方法进行系数拟合。该方法认为在双对数曲线中每一特征段内只有一种噪声起主导作用，根据 Allan方差拟合曲线不同斜率确定不同噪声的分段点，利用曲线分段外推各个噪声系数。但在实际光纤陀螺噪声分析中，每个频域都可能存在噪声，因此准确找到每一噪声的分界点较为困难，甚至在某特定的τ域内相关时间相近的两种噪声在Allan方差都有贡献，对其进行连续分段后利用对应多项式拟合可能产生较大误差。

以陀螺1为例，利用上述方法对长时间的测试数据进行分段 Allan方差分析，其中一组数据的 Allan方差拟合曲线在0～300 s的斜率如图5所示。

从图5可以看出，较短相关时间的噪声（对应量化噪声和随机游走噪声）的 Allan方差曲线斜率并不是由-1变为-1/2的折线，因此量化噪声和随机游走噪声的相关时间没有明确的界限，在短时间内该两种类型噪声对 Allan方差都有贡献，并不能通过斜率来直接划分噪声相关时间分界点。

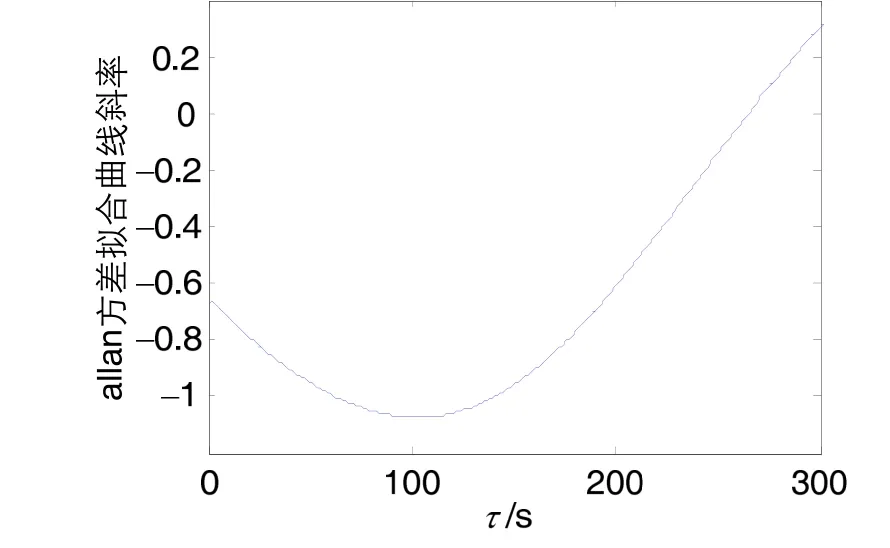
图5 陀螺1的 Allan方差斜率Fig.5 Slope of Allan variance curve of FOG 1

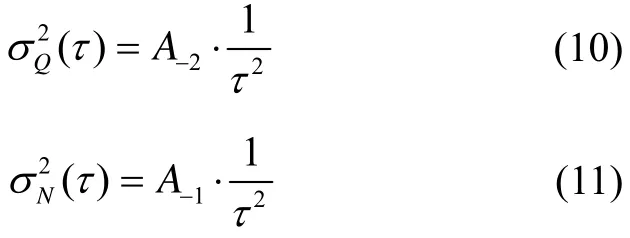
分段拟合系数为A-2=0.12和A-1=0.001387，拟合曲线如图6和图7所示，从图可以看出，其两个分段内都存在较大拟合误差，其中系数A-2误差尤为明显，拟合均方差分别为0.09270.0677

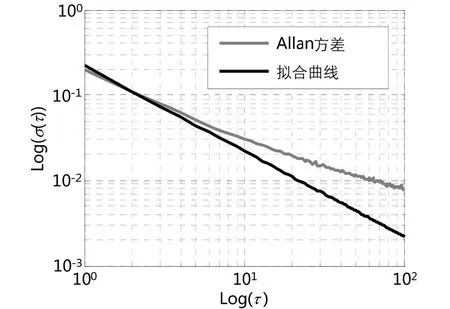
图6 陀螺1的 Allan方差拟合曲线（第1段）Fig.6 Allan variance fitting curve of FOG 1 in section 1

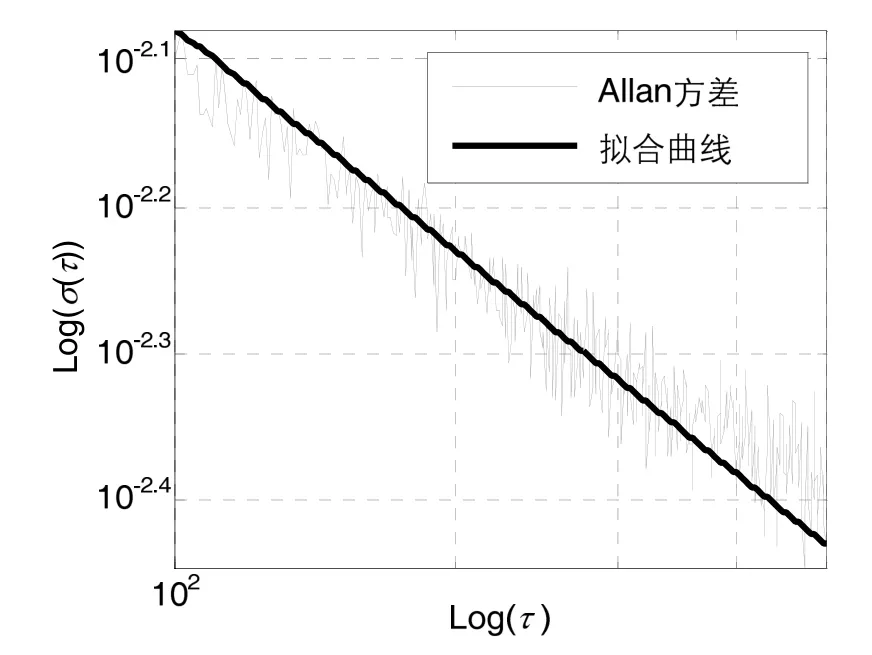
图7 陀螺1的 Allan方差拟合曲线（第2段）Fig.7 Allan variance fitting curve of FOG 1 in section 2

因此在一定的τ域内，相关时间相近的两种噪声对 Allan方差都有贡献，连续分段拟合的方法难以准确估计出光纤陀螺的各噪声成分系数。

3.2 重叠分段Allan方差分析

针对上述方差分析出现的问题，提出一种基于重叠分段的光纤陀螺噪声分析方法。该方法根据 Allan方差双对数曲线及噪声相关时间特点对τ域进行重叠混合分段，根据τ域内的噪声成分和特点，将相关时间相近的不同噪声化为同一区段；同时，为减小相邻区段噪声的方差贡献带来的拟合误差，拟合时将相邻频段内τ的幂次项纳入拟合模型。由于速度游走和速率斜坡系数相关时间较长，现以2只陀螺的10组长时间测试数据进行分析。限于篇幅，给出其中1组数据的分析过程和拟合曲线，10组数据的分析结果在后文列表中给出。

根据各噪声的特点和相关时间，选取第一区段为0～500 s，此区段内的噪声主要为量化噪声和随机游走，同时考虑零偏不稳定性噪声的影响，将拟合模型选为：

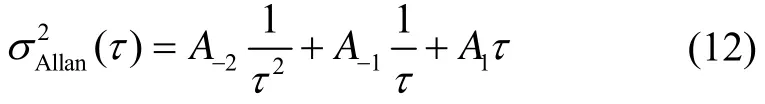
据此，对其中1组长时间测试数据输出的模型拟合的结果如图 8所示，其拟合系数为A-2=0.1625，，拟合均方差为0.0293。陀螺2的拟合系数为，拟合均方差为 0.0216。A0加入模型只是为了减小拟合误差，其值不予采信，其系数将在其主要作用区段内进行拟合。

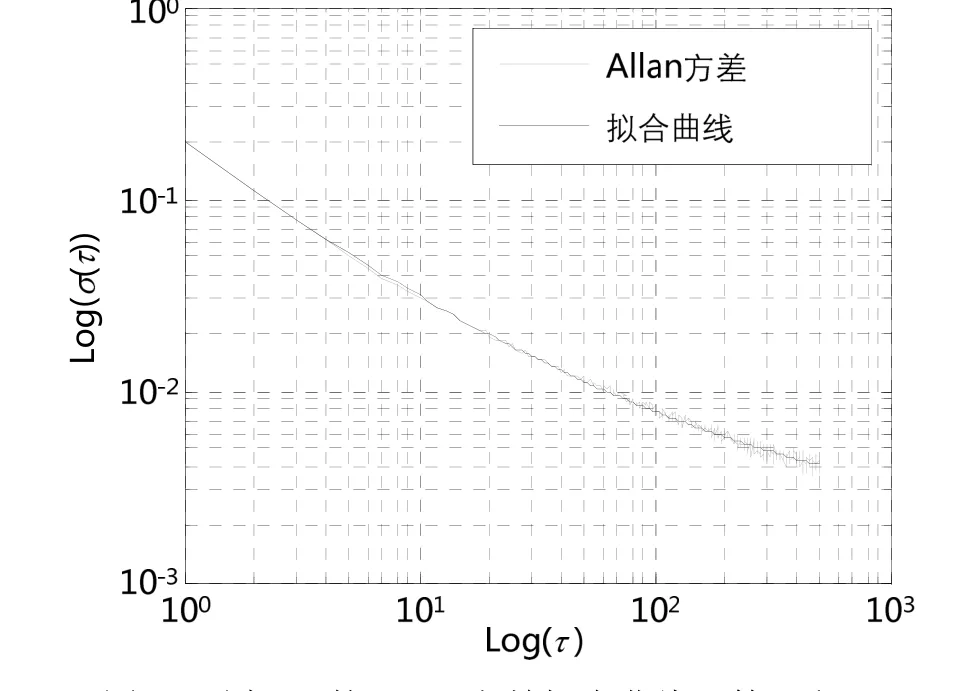
图8 陀螺1 的Allan方差拟合曲线（第1段）Fig.8 Allan variance fitting curve of FOG 1 in section 1

选取第二区段为300～3 000 s，此区段内的噪声主要为零偏不稳定性噪声，同时考虑随机游走和速率游走的影响，其拟合模型为：

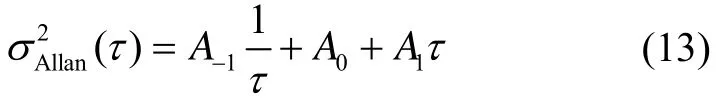
据此，对其中1组长时间测试数据输出的模型拟合的结果如图9所示，拟合系数为A0=6.5427×10-3，拟合均方差为0.032 0。Y陀螺的拟合系数为A0=5.257 7 ×10-3，拟合均方差为0.035 4。

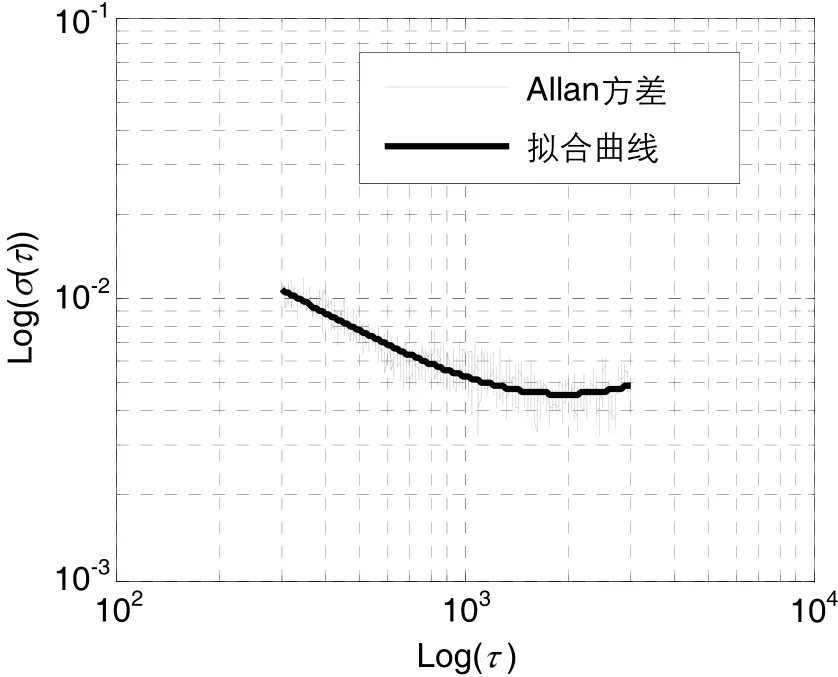
图9 陀螺1 Allan方差拟合曲线（第2段）Fig.9 Allan variance fitting curve of FOG 1 in section 2

第三区段1000～10 000 s，此区段内的噪声主要为速率游走和速率斜坡噪声，同时考虑零偏不稳定性的影响，其拟合模型为：

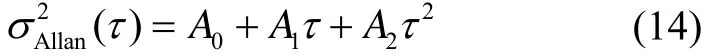
据此，对其中1组长时间测试数据输出的模型拟合结果如图10所示，拟合系数为，拟合均方差为0.02878。陀螺2的拟合系数为拟合均方差为0.02545。

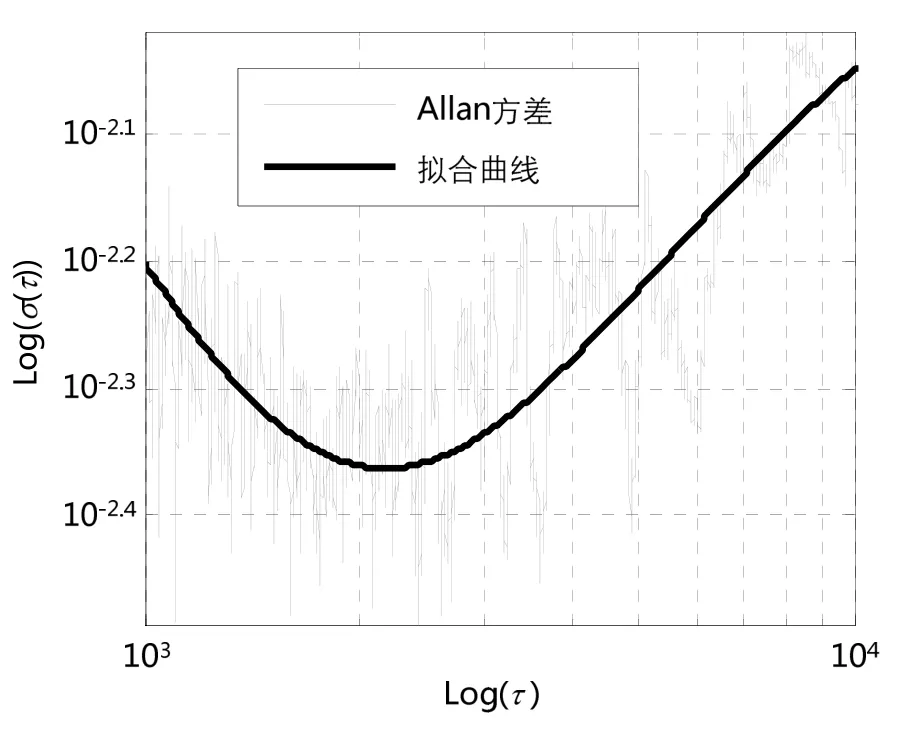
图10 陀螺1 Allan方差拟合曲线（第3段）Fig.10 Allan variance fitting curve of FOG 1 in section 3

上述分析可知，重叠分段 Allan方差分析方法的拟合均方差均小于连续分段Allan方差分析方法。

利用连续分段 Allan方差分析方法和重叠分段Allan方差分析方法，分别对2只陀螺的10组长时间测试数据进行分析。为清楚显示，将两种分析方法对2只光纤陀螺长时间测试数据的噪声系数分析结果和拟合均方差的均值列入表4和表5。

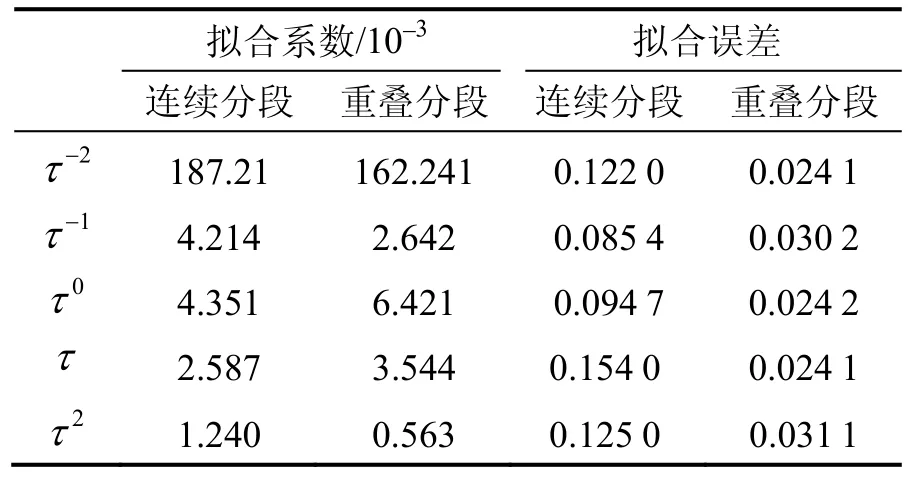
表4 两种分段Allan方差分析结果（陀螺1）Tab.4 Result of two variance analysis methods(gyro 1)

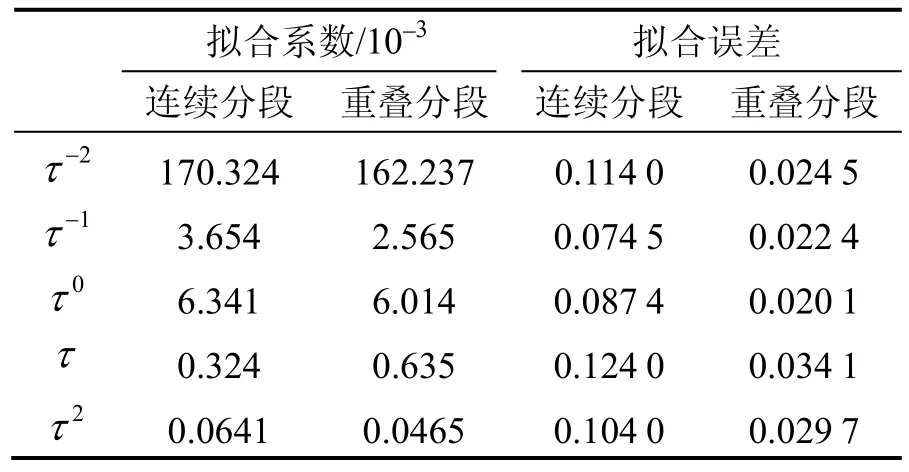
表5 两种分段Allan方差分析结果（陀螺2）Tab.5 Result of two variance analysis methods(gyro 2)

从表4和表5可以看出，重叠分段的Allan分析方法拟合误差比连续分段分析方法减小了2/3。同时，比较表4和表5可知，重叠分段分析中两个陀螺的量化噪声相当，而连续分段分析中该项系数变化较大。由于两个陀螺均采用同一块采样计数电路，因此量化噪声相当，故重叠分段分析结果更加可信。同时，两陀螺的随机游走和零偏不稳定性噪声相当，与陀螺标称性能符合。但陀螺1的速率游走和速率斜坡项较大，与之相比陀螺2的性能更为优越。由于进行了混合分段，减小了在噪声成分分布不均匀时，利用总体五项多项式拟合造成的拟合误差，隔离了不同类型噪声对相关时间相差较远的噪声拟合系数的影响。同时，也避免了相关时间相近的噪声被连续分段隔离而导致其系数拟合误差。

4 结 论

针对光纤陀螺随机误差的特点，提出了一种重叠分段 Allan方差分析方法，有效估计出光纤陀螺各种噪声成分系数。首先，分析了常规 Allan方差分析中出现噪声拟合系数为负的原因，探讨了利用经典方差方法分析的前提。其次，在分析连续分段 Allan方差拟合方法后，指出该方法人为分离了相关时间相近的噪声成分，将导致较大拟合误差。最后，提出了重叠分段的Allan方差分析方法，该方法根据噪声特点对相关时间进行混合重叠分段，在不同分段内对不同噪声的 Allan方差曲线进行拟合，有效估计各噪声成分系数。光纤陀螺实测数据的分析结果表明，该方法的拟合误差比连续分段Allan方差分析方法减小2/3。

（References）：

[1] 李颖, 陈兴林, 宋申民. 光纤陀螺误差动态 Allan方差分析[J]. 光电子激光, 2008, 19(2): 182-186. Li Ying, Chen Xing-lin, Song Shen-min. Dynamic Allan variance analysis for the drift error of fiber optical gyroscope[J]. Journal of Optoelectronics · Laser, 2008, 19(2): 182-186.

[2] IEEE Std 647™-2006. IEEE standard specification format guide and test procedure for single-axis laser gyros[S]. New York: IEEE Aero Space and Electronic Systems Society, 2006.

[3] Morrow R B, Heckman D W. High precision IFOG insertion into the strategic submarine navigation system [C]//Proceedings of the Position Location and Navigation Symposium. USA: IEEE, 1998: 332-338.

[4] Killian K. High performance fiber optic gyroscope with noise reduction[C]//SPIE Proceedings. Denver, 1994: 255-263.

[5] Charles A, Greenhall, Dave A, et al. Total variance: an estimator of long-term frequency stability[J]. IEEE Transaction on Ultrasonic Ferroelectrics, and Frequency Control, 1999, 46(5): 1183-1191.

[6] Howe D A, Tasset T N. Theol: characterization of very long-term frequency stability[C]//EFTF 04．Proceeding of the 18th European Frequency and Time Forum. Guildford: University of Surrey, 2004: 581-587.

[7] Tehrani M. Ring laser gyro sata-analysis with cluster sample technique[C]//Proceedings of SPIE - The International Society for Optical Engineering. USA, 1983: 207-220.

[8] 闾晓琴, 张桂才. 采用分段法估算Allan方差中的各噪声系数[J]. 压电与声光, 2009, 31(2): 166-167. Lü Xiao-qin, Zhang Gui-cai. Estimation of various noise factors from allan variance by subsection method[J]. Piezoelectectrics & Acoutooptics, 2009, 31(2): 166-167.

[9] 张梅, 张文. 激光陀螺随机漂移的研究方法（一）[J].中国惯性技术学报, 2009, 17(2): 210-213. Zhang Mei, Zhang Wen. Research method on drift of ring laser gyro(I)[J]. Journal of Chinese Inertial Technology, 2009, 17(2): 210-213.

[10] 张梅, 张文. 激光陀螺随机漂移的研究方法（二）[J].中国惯性技术学报, 2009, 17(3): 350-355. Zhang Mei, Zhang Wen. Research method on drift of ring laser gyro(II)[J]. Journal of Chinese Inertial Technology, 2009, 17(3): 350-355.

[11] 高伯龙, 王关根. 陀螺数据的数学处理[J]．国防科学技术大学学报, 1979(1): 91-106. Gao Bo-long, Wang Guan-gen. Mathematical treatment of gyro data[J]. Journal of National University of Defense Technology, 1979(1): 91-106.

[12] 李京书, 许江宁, 査峰, 等. 基于6类噪声项拟合模型的光纤陀螺噪声特性分析方法[J]. 兵工学报, 2013, 34(7): 835-839. Li Jing-shu, Xu Jiang-ning, Zha Feng, et al. Analysis method for the noise characteristics of fiber optic gyroscope based on fitting model of six noise items[J]. Acta Armamentarii, 2013, 34(7): 835-839.

Overlap-section Allan variance analysis method for FOG random errors

CHEN Yong-bin, ZHA Feng, LIU Yong

(Navigation Engineering Department, Naval University of Engineering, Wuhan 430033, China)

According to the characteristic of the random errors of fiber optic gyro (FOG), an Allan variance analysis method is proposed, which can effectively evaluate the different noise coefficients. First, the reason why the fitting coefficient of Allan variance is negative is discussed, and the premise that traditional variance method used to analyze is given. Then, the piecewise fitting method for Allan variance curve is studied. In this method, the Allan variance curve is piecewise fitted according to different correlation time of different noises, but the noises with similar correlation time are separated rigidly, which could cause fitting errors. Therefore a overlapping piecewise fitting method for Allan variance curve is proposed, in which the different noises with similar correlation time are divided into the same fitting section. The items of polynomial in the adjacent section are added into the fitting model to improve the fitting precision. The analysis results of FOG test data indicate that, compared to those of the piecewise fitting of Allan variance, the fitting errors of the proposed method are reduced by one-third.

Allan variance; fiber optic gyro; random error; piecewise fitting

U666.1

A

1005-6734(2016)02-0235-07

10.13695/j.cnki.12-1222/o3.2016.02.018

2015-12-25

2016-03-20

国家自然科学基金（61503404，41574069）；海军工程大学青年自然科学基金（HGDYDJJ15006）

陈永冰（1964—），男，教授，从事组合导航研究。E-mail: hgcyb@163.com

联 系 人：查峰（1984—），男，讲师，博士。E-mail: zha_feng@126.com