惯导速度辅助接收机跟踪环路算法

傅金琳，赵子阳，李醒飞，刘红光，胡 才

（1. 天津大学 精密仪器与光电子工程学院，天津 300072；2. 天津航海仪器研究所，天津 300131）

惯导速度辅助接收机跟踪环路算法

傅金琳1,2，赵子阳2，李醒飞1，刘红光2，胡 才2

（1. 天津大学 精密仪器与光电子工程学院，天津 300072；2. 天津航海仪器研究所，天津 300131）

针对接收机在强干扰高动态环境难以定位导航的问题，提出基于惯导速度辅助卫星跟踪环路算法，通过惯导速度估算环路多普勒频移，压缩了环路需承载的动态范围，从而减少了环路等效噪声带宽，进而降低了跟踪环路带内干扰，提高了卫星接收机抗干扰能力。对提出算法的普适性、动态性、抗干扰性以及惯导估算误差影响等方面进行了仿真评估，仿真结果验证了算法的正确性，同时证明提出算法相比传统算法，载体运动加速度由91g提升至193g，同时抗干扰能力提升5~8 dB，可以容忍较大惯导辅助信息误差，为算法工程化奠定了基础。

惯导速度辅助；高动态；抗干扰性；惯导辅助信息误差

从图1可知，经过A/D转换后的数字中频信号，通过混频器和相关器后获得剥离载波和伪随机码的信号，而后通过积分清零、环路鉴别器获得环路相位误差，经过环路滤波器平滑后，用以校正载波NCO。传统载波跟踪环路中，在外界气候环境一定的情况下，环路稳定性主要受到载体动态性和外来干扰的影响。当载体动态性过大时，由于引入跟踪环路误差过大，将导致跟踪环路失锁。外来干扰过大也将导致跟踪环路失锁。增大跟踪环路带宽能够提升环路动态性能，但将引入更大的噪声干扰。为解决动态性和噪声对跟踪环路带宽要求的矛盾，本文提出了惯导速度辅助的载波环路跟踪算法。

2 惯导速度辅助环路跟踪算法

2.1 信号模型

图2给出了基于惯导速度辅助载波跟踪环路的原理框图。对比图1可知，该跟踪环路用环路鉴别误差和惯导速度辅助信息共同对载波 NCO进行修正，通过惯导速度辅助减小卫星跟踪环路所需承载的载波相位误差范围。

图2 惯导速度辅助载波跟踪环路框图Fig.2 INS velocity-aided Carrier tracking loop

为了方便分析惯导速度辅助的优势，图3只给出了图2中环路鉴别器输出至载波NCO输入前的原理图，其中虚线框中为惯导速度辅助部分，是惯导辅助滤波系数，e(s)为惯导速度辅助引入的误差，w(s)为原跟踪环路中的热噪声等，F(s)为原跟踪环路的滤波环路系数：

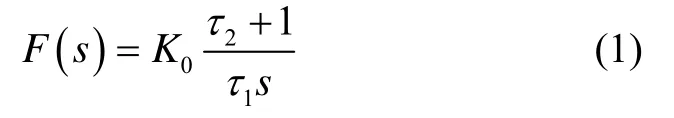
式中，K0为环路滤波器的增益，τ1和τ2为滤波器的时间常数。

图3 惯导速度辅助载波跟踪滤波环路原理图Fig.3 INS velocity-aided Carrier tracking filter loop

假设惯导速度能够无误差估算载波的多普勒频移，即e(s)为0，则有：

式中，

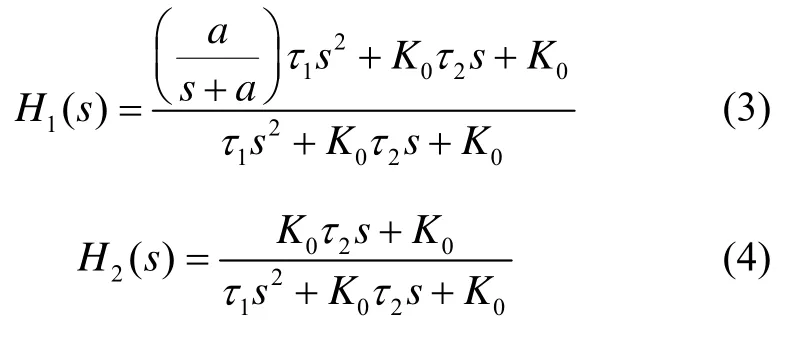
由式(3)可以看出，当惯导系统的带宽趋向于无穷大，即a→∞时，系统传递函数 H1(s)→1，这说明只要惯导系统的带宽足够大，惯导速度辅助的跟踪环就可以跟踪载体的任何机动形式。

2.2 多普勒频移计算

惯导速度对卫导接收机载波跟踪环路辅助主要是用到惯导提供的载体速度信息、载体位置信息以及卫星星历提供的卫星速度信息和卫星位置信息估算载波多普勒频移，用估算的多普勒频移对载波跟踪进行辅助。多普勒频移的具体计算公式为

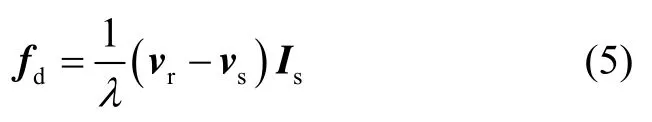
式中： fd表示载波多普勒频移；λ表示载波波长，这里为GPS L1频点载波波长；vr表示接收机天线速度，vs表示卫星速度， Is为卫星到接收机视线上的单位矢量。卫星速度、卫星位置、载体速度、载体位置的估算误差将直接导致估算的载波多普勒频移误差。

3 仿真分析

分别基于卫星信号模拟器和中频信号生成软件考察惯导速度辅助载波跟踪环路的性能。卫星信号模拟器和中频信号生成软件仿真的是GPS L1频点数据，载波频率为1757.42 MHz，C/A码速率为1.023 MHz，采用频率为62 MHz，中频频率为8.58 MHz。

3.1 普适性仿真

普适性仿真目的是考察惯导速度辅助是否对同时看到的所有卫星跟踪有效。仿真采用卫星信号模拟器产生卫星信号，其中载体的初始速度为北向10 m/s，加速度为北向10 g。此时能够捕获的卫星有2、5、7、8、10、15、26、29号星。根据此时卫星和载体的相对位置，映射到每颗星连线上的加速度数值依次约为71 m/s2、23 m/s2、67 m/s2、19 m/s2、15 m/s2、24 m/s2、0.16 m/s2、7 m/s2。

卫导跟踪环路采用三阶锁相环跟踪，环路带宽为 2 Hz。加和不加惯导速度辅助的环路跟踪结果如图4所示。

图4 2号星跟踪结果Fig.4 Tracking results of the satellite 2

从图4可以看出，当载体动态较大时，采用无辅助跟踪环路I路累积值快速减小，在0值附近振荡，即环路失锁。增加惯导速度辅助后，环路经过一定时间振荡后，最终达到稳定跟踪。可见，增加惯导信息辅助能够改善卫星跟踪环路的动态性能。

图5 7号星跟踪结果Fig.5 Tracking results of the satellite 7

图5同样表明了增加惯导速度辅助的优势。对比图4、图5可知，当载体动态性减小时，所需稳定跟踪时间缩短。

图6~图10同样表明，增加惯导速度辅助能改善卫星跟踪环路的动态性，同时表明，当载体动态性不大的时候，惯导速度辅助能够使卫星跟踪环路迅速稳定。

从图11可知，当载体动态性较小时，无惯导信息辅助，窄的跟踪环路带宽也能实现环路的稳定跟踪，与采用惯导速度辅助跟踪结果类似，惯速度辅助的效果不明显。也就是说，载体动态性不大的情况下，无需采用惯导速度辅助。

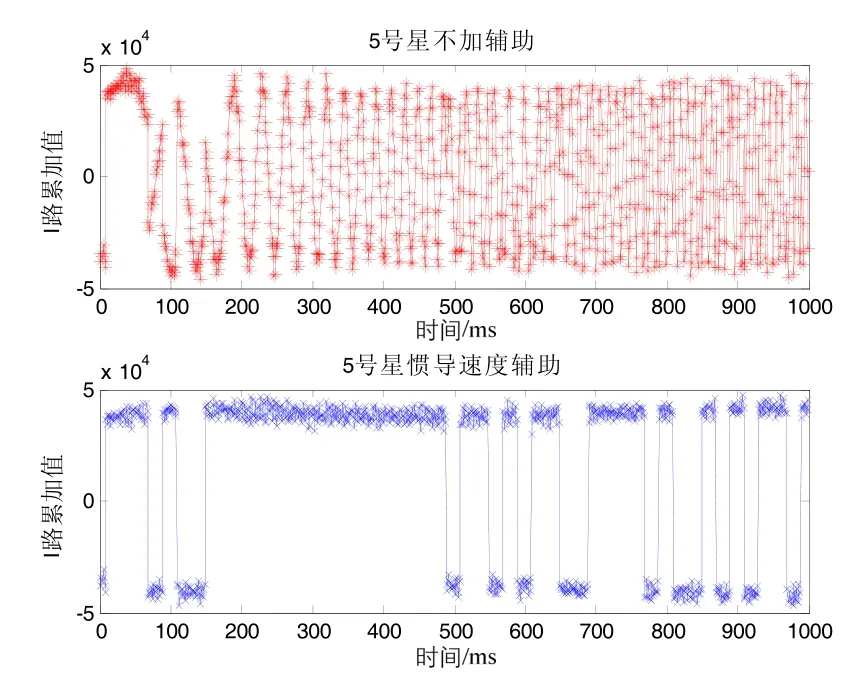
图6 5号星跟踪结果Fig.6 Tracking results of the satellite 5

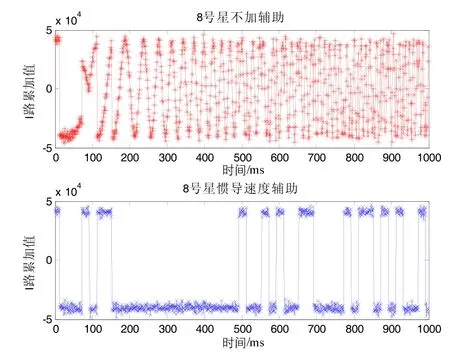
图7 8号星跟踪结果Fig.7 Tracking results of the satellite 8

图8 10号星跟踪结果Fig.8 Tracking results of the satellite 10

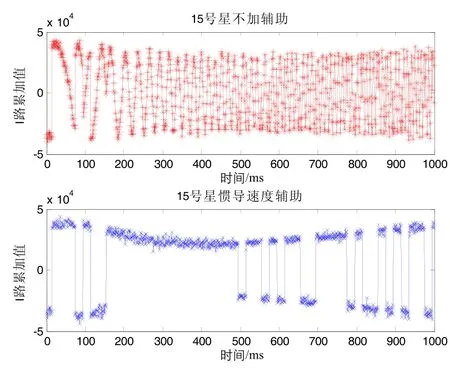
图9 15号星跟踪结果Fig.9 Tracking results of the satellite 15

图10 29号星跟踪结果Fig.10 Tracking results of the satellite 29

图11 26号星跟踪结果Fig.11 Tracking results of the satellite 26

综合图4~图11可知，通过惯导速度辅助，卫导跟踪环路能够在较小的带宽下实现对较大动态范围的稳定跟踪。此外，惯导速度辅助能够对同一时刻所有卫星的跟踪环路进行有效辅助，证明了算法的普适性和正确性。

3.2 动态性仿真

基于自编中频信号生成数据对惯导速度辅助跟踪环路算法的动态性进行评估。本仿真的目的是考察有无惯导速度辅助下，跟踪环路承载动态应力能力的差异。由于无定位结果，本仿真中以I路累加值无误判且环路锁定为前提条件，在次前提下比较有无惯导速度辅助跟踪环路能够承载的最大动态应力，所得有无惯导速度辅助跟踪环路承载的最大动态应力与实际接收机存在差异，这里只关注二者的差异。信号加噪声为高斯白噪声，信号信噪比为-19 dB，即接收信号功率为-130 dBm，采样率为62 MHz。仿真结果如图12和图13所示。从图12可知：当载体加速度为91g时，无惯导信息辅助环路能够实现稳定跟踪；在载体加速度为92g时，无惯导信息辅助环路I路累加值逐渐在0值周围波动，即环路不再能稳定跟踪，即无惯导信息辅助环路最大能承受的载体加速度为91g。从图13可知：当载体加速度为193g，惯导速度信息辅助环路能稳定跟踪；当载体加速度为194g时，I路累加值在0上下频繁波动，惯导速度辅助环路不再能稳定跟踪。可见惯导速度辅助环路能够承载的载体最大加速度为193g。对比图12、图13可知，采用惯导速度辅助卫导跟踪环路，能极大提升跟踪环路的动态性。

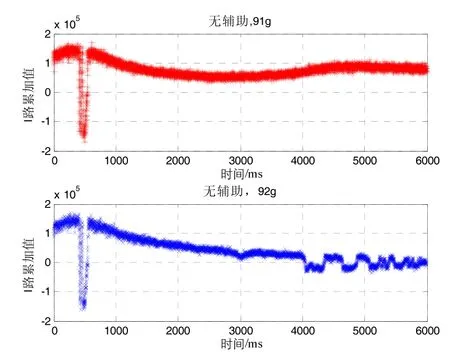
图12 无惯导辅助跟踪环路动态性Fig.12 Dynamics of tracking loop without INS-aided

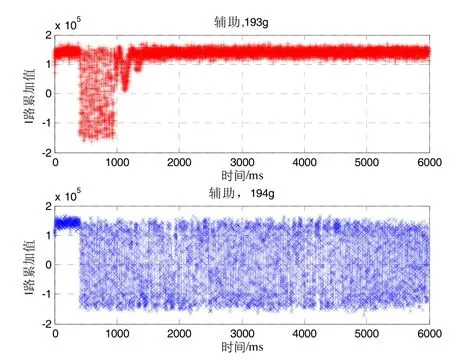
图13 惯导辅助跟踪环路动态性Fig.13 Dynamics of tracking loop with INS-aided

3.3 抗干扰性仿真

采用惯导速度对载波跟踪环路进行辅助，能够极大程度上削弱载波环路需要承受的动态应力，理想情况下环路带宽只需满足热噪声误差需求，因此能够将载波环路带宽设计的非常小。载波环路带宽的缩小，将减少信号带宽内的噪声干扰。

基于自编中频信号生成数据对惯导速度辅助跟踪环路算法的抗干扰性进行评估，所加噪声为高斯白噪声，采样率为 62 MHz，选择匀速直航、加速度 50g两种典型环境进行考察。环路跟踪判决采用第3.2节判决依据。

当匀速直航时，无惯导信息辅助环路能够跟踪信噪比为-31 dB的卫星信号，惯导速度信息辅助环路能够跟踪信噪比为-36 dB的卫星信号，大约提高了5 dB抗干扰能力。仿真结果如图14和图15所示。

根据上述判决条件，仿真得到当加速度为50g时，无惯导信息辅助环路能够跟踪信噪比为-28 dB的卫星信号，惯导速度信息辅助环路能够跟踪信噪比为-36 dB的卫星信号，大约提高了8 dB抗干扰能力。仿真结果如图16和图17所示。

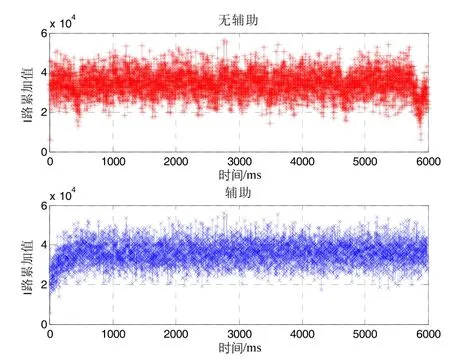
图14 匀速时，信噪比-31 dB时，有无惯导辅助环路跟踪结果Fig.14 Loop tracking results with and without INS-aided when velocity is constant, SNR= -31dB

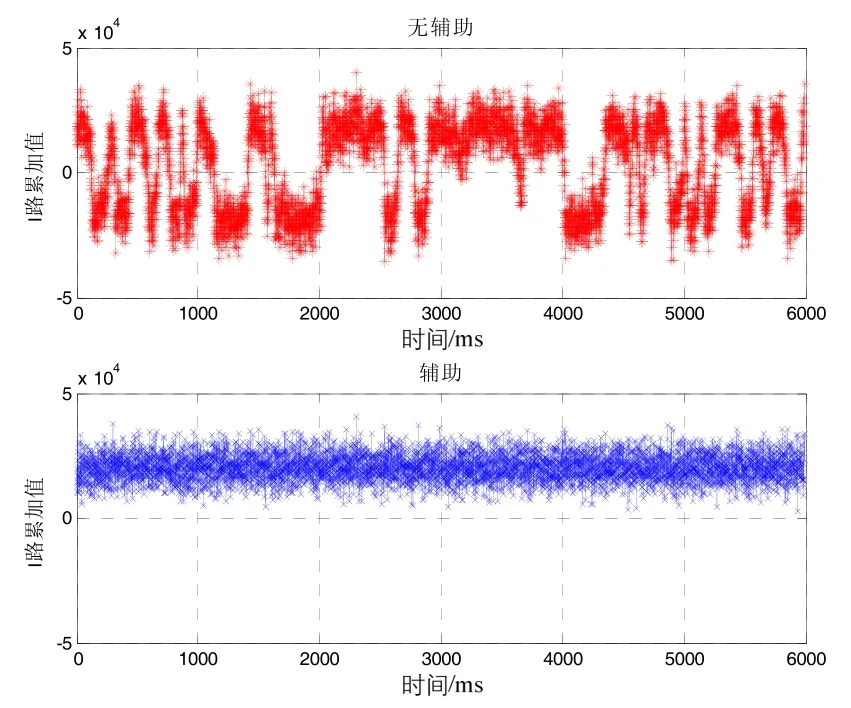
图15 匀速时，信噪比-36 dB时，有无惯导辅助环路跟踪结果Fig.15 Loop tracking results with and without INS-aided when velocity is constant, SNR= -36 dB

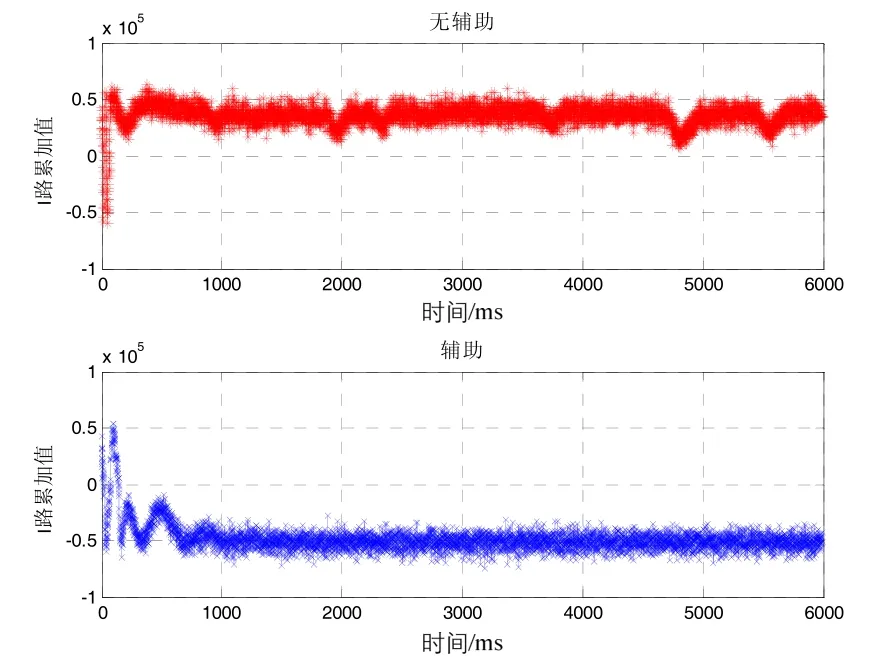
图16 加速度50g，信噪比-28 dB时，有无惯导辅助环路跟踪结果Fig.16 Loop tracking results with and without INS-aided when acceleration is 50g, SNR= -28 dB

图17 加速度50g，信噪比-36 dB时，有无惯导辅助环路跟踪结果Fig.17 Loop tracking results with and without INS-aided when acceleration is 50g, SNR= -36dB

3.4 不同精度惯导速度辅助仿真分析

为了充分评估惯导信息计算的载波多普勒误差对跟踪环路影响，分别采用在多普勒频率真值加高斯白噪声误差和模拟惯导误差计算辅助载波多普勒的方式。第一种方式中，选取载体三个运动场景作为典型环境：1）匀速直航；2）加速度为50g，3）加速度为193g。第二种方式中，惯导信息采用主惯导输出，陀螺常值漂移0.01°，随机游走噪声0.001 (°)/√h，加表零偏10-5g，加表随机噪声10-6g。上述仿真中，信号信噪比都为-19 dB。

图18给出了匀速直航时，载波多普勒估算误差分别为1 Hz、6 Hz、7 Hz时，惯导速度辅助卫导跟踪环路的跟踪结果。

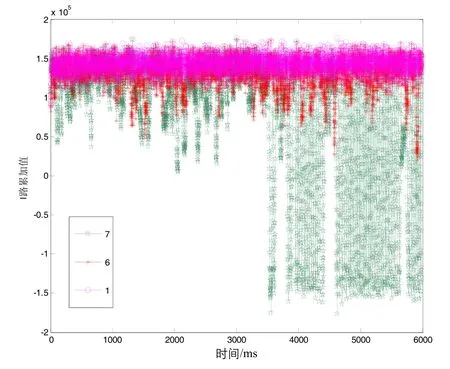
图18 匀速时，不同载波多普勒误差下，惯导辅助跟踪结果Fig.18 INS-aided tracking results with different carrier Doppler errors when velocity is constant

从图18可以看出：载波多普勒估算偏差在6 Hz以内时，采用惯导速度辅助能实现稳定跟踪；当载波多普勒估算偏差为7 Hz时，跟踪环路不再稳定。可见环路能够承受的最大多普勒频移估算误差为6 Hz。

图19给出了匀速直航时，采用模拟惯导误差计算的载波多普勒辅助的跟踪结果。从图19中可以看出，I路累加值都大于0，即不会出现数据位的误判，也就是说环路能够稳定跟踪。

图20给出了加速度为50g，载波多普勒估算误差分别为1 Hz、5 Hz、6 Hz时，惯导速度辅助卫导跟踪环路的跟踪结果。从图20可以看出，载波多普勒估算偏差在5 Hz以内时，采用惯导速度辅助能实现稳定跟踪，可见动态性增大，环路对估算误差的承受力也随之降低。

图21给出了加速度为50g时，采用模拟惯导误差计算的载波多普勒辅助的跟踪结果。从图21中可以看出，I路累加值都大于0，即不会出现数据位的误判，也就是说环路能够稳定跟踪。

图19 匀速时，采用惯导误差计算载波多普勒辅助跟踪结果Fig.19 Carrier Doppler-aided tracking results calculated by INS error when velocity is constant

图22给出了加速度为193g，载波多普勒估算误差分别为1 Hz、5 Hz、6 Hz时，惯导速度辅助卫导跟踪环路的跟踪结果。从图22可以看出，载波多普勒估算偏差在5 Hz以内时，采用惯导速度辅助能实现稳定跟踪。

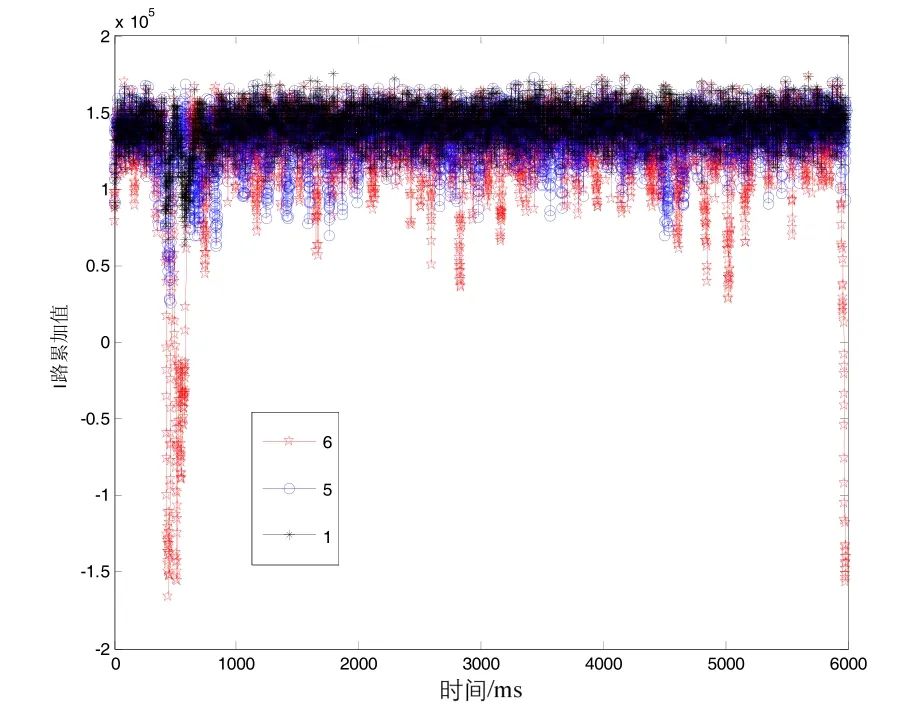
图20 加速度50g时，不同载波多普勒误差下，惯导辅助跟踪结果Fig.20 INS-aided tracking results with different carrier Doppler errors when acceleration is 50g

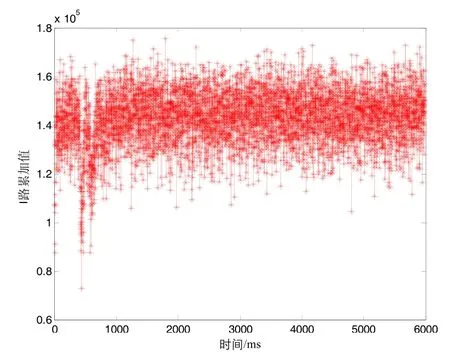
图21 加速度50g时，采用惯导误差计算载波多普勒辅助跟踪结果Fig.21 Carrier Doppler-aided tracking results calculated by INS error when acceleration is 50g

图22 加速度193g时，不同载波多普勒误差下，惯导辅助跟踪结果Fig.22 INS-aided tracking results with different carrier Doppler errors when acceleration is 193g

图23给出了加速度为193g时，采用模拟惯导误差计算的载波多普勒辅助的跟踪结果。从图23中可以看出，I路累加值都大于0，即不会出现数据位的误判，也就是说环路能够稳定跟踪。

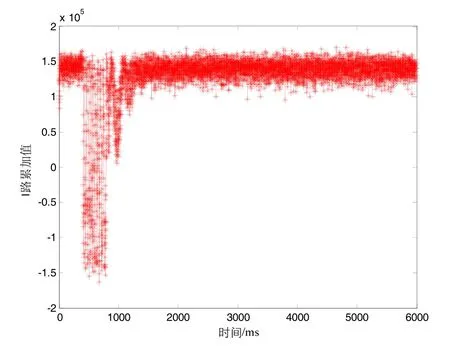
图23 加速度193g时，采用惯导误差计算载波多普勒辅助跟踪结果Fig.23 Tracking results aided by carrier Doppler calculated by INS error when acceleration is 193g

此外，考察了同一时刻惯导位置误差和速度误差对不同卫星载波多普勒的估算误差，当惯导位置误差在1000 m以内，速度误差不超过0.4 m/s时，引起的载波多普勒估算误差不大于5 Hz。从而可知，深组合导航方式时，导航级惯导都满足上述指标要求。

4 结 论

本文首先分析了惯导速度辅助卫导跟踪环路算法的原理，而后分别对惯导速度辅助卫星跟踪环路算法的普适性、动态性、抗干扰性以及环路辅助对惯导信息精度需求进行了仿真分析。仿真结果证明，惯导速度辅助对同一时刻所有可见星均有效，即证明了提出算法的正确性。此外，仿真结果表明：本文提出的算法的动态性比传统跟踪环路提升了约100g，抗干扰能力在不同动态环境下提升程度不同，约提升 5~8 dB，动态性越高的环境抗干扰能力提升越明显；卫星跟踪环路对辅助的惯导信息精度要求不高，导航级惯导即能满足跟踪环路辅助的精度需求，动态性越大的环境对惯导辅助信息精度要求越高。

（References）：

[1] Mahmoud A R. Tightly coupled integration of GPS precise point positioning and MEMS-based inertial systems[J]. GPS Solution, 2015, 19(4): 601-609.

[2] Youssef T, Phillip T, Cynl B, et al. Implementation and performance of a GPS/INS tightly coupled assisted PLL architecture using MEMS inertial sensors[J], Sensors, 2014, 14(2): 3768-3796.

[3] Bach-Phi D, Vinh-Hao N. Development of a GPS/INS integrated navigation system for model aircraft[C]// International Conference on Control, Automation and Systems. 2014: 201-206.

[4] Li C J, Yang S X. Optimization of the carrier tracking loop for GPS high dynamic receivers[J]. Journal of Beijing Institute of Technology, 2012, 21(2): 164-171.

[5] 赵琳, 赵洪斌, 闫超. 复杂环境下INS辅助GPS跟踪环路研究[J]. 传感器与微系统, 2011, 30(10): 22-25. Zhao Lin, Zhao Hong-bin, Yan Chao. Study on tracking loops of INS-aided GPS in complex environment[J]. Transducer and Microsystem Technologies, 2011, 30(10): 22-25.

[6] 李传军, 李兴城. 一种基于 VDLL和 CaKFPLL的INS/GNSS超紧耦合方法[J]. 中国惯性技术学部, 2013, 21(6): 669-774. Li Chuan-jun, Li Xing-cheng. INS/GNSS ultra-tight coupling based on VDLL and CaKFPLL[J]. Journal of Chinese Inertial Technology, 2013, 21(6): 669-774.

[7] Lin T, Curran J T, O’Driscoll C, et al. Implementation of a navigation domain GNSS signal tracking loop[C]//24th International Meeting of the Satellite Division of the Institute of Navigation. Fairfax, VA: Institute of Navigation, 2011: 3644-3651.

[8] 吕鹏, 陆明泉, 冯振明. 一种惯导辅助卫星导航三阶载波PLL算法[J]. 计算机仿真, 2013, 12(30): 13-16. LV Peng, Lu Ming-quan, Feng Zhen-ming. Algorithm of three order satellite navigation carrier PLL loop aided by INS[J]. Computer Simulation, 2013, 12(30): 13-16.

[9] Li Peng, Chen Zhoug-gui, Zheng Jin-jin. High dynamic signal pulling with biased doppler aiding from INS[C]// International Conference on Electrical and Control Engineering. 2011: 676-679.

[10] 刘苑伊, 赵昀, 耿生群. 基于 INS辅助的高动态 GPS接收机算法研究[J]. 计算机工程与设计, 2011, 32(3): 1096-1098. Liu Yuan-yi, Zhao Yun, Geng Sheng-qun. Research on INS aided high dynamic GPS receiver algorithm[J]. Computer Engineering and Design, 2011, 32(3): 1096-1098.

[11] Mahmoud A R, EI-Rabbany A. Non-linear filtering for precise point positioning GPS/INS integration[J]. International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, 2014, 40(2): 127-132.

[12] Liu Gang, Guo Mei-feng, Zhang Rong, et al. Hardwareimplementable vector tracking loop for GNSS/INS deep integration[J]. Journal of Chinese Inertial Technology, 2015, 23(2): 189-195.

INS velocity-aided receiver tracking loop algorithm

FU Jin-lin1,2, ZHAO Zi-yang2, LI Xing-fei1, LIU Hong-guang2, HU Cai2
(1. Tianjin University School of Precision Instrument and Opto-electronics Engineering, Tianjin 300072, China; 2. Tianjin Navigation Instruments Research Institute, Tianjin 300131, China)

In view that the receiver of inertial navigation system (INS) is hard to locate and navigate in high dynamic and noisy environment, an INS velocity-aided satellite tracking loop algorithm is proposed. The tracking loop’s Doppler shift is estimated by INS velocity, which compresses the needed dynamic range of the tracking loop, thereby decreases the equivalent noise bandwidth of the loop, reduces the tracking loop in-band interference, and improves the anti-jamming ability of satellite receiver. Simulations are made to test the proposed algorithm’s universality, dynamicity, anti-interference capacity and its influences on INS’s estimation errors, and the results prove the correctness of the algorithm and show that the proposed algorithm upgrades the vehicle acceleration to 193g compared to 91g by traditional methods, improves the antiinterference ability by 5-8 dB, and can tolerate large estimation error of INS-aided information. These lay the foundation for the algorithm engineering.

inertial navigation system; velocity-aided; high dynamic; anti-jamming; INS-aided information error

U666.1

：A

1 传统载波跟踪环路结构

1005-6734(2016)03-0330-07

10.13695/j.cnki.12-1222/o3.2016.03.010

2016-03-30；

：2016-04-12

船舶预研支撑技术基金项目（14JZ3.9.2）

傅金琳（1984—），女，博士后，高级工程师，研究方向为综合导航技术。E-mail: linkimf@163.com

卫星导航系统日益成熟，推动着卫导接收机在军事和民用领域的应用拓展。复杂环境下导航服务的精确性和连续性成为核心技术，其中卫导跟踪环路的性能至关重要[1-3]。当载体动态性过大时，卫星信号多普勒频率变化率劣化，导致传统环路失锁，接收机难以正常工作[4-7]。基于这个问题，主要有三种解决方式：一是通过增加环路带宽，这将导致环路噪声加大，可能导致环路干扰过大而失锁；二是采用高阶锁相环，这种环路不但设计难度大，且稳定度不高，难以保证接收机稳定跟踪；三是引入辅助信息，减小载体的动态应力误差。国内外文献对于采用惯导信息辅助卫导跟踪环路进行了大量研究[8-12]，研究成果集中于理论分析惯导速度辅助对环路带宽的影响，对于辅助实现方式和环路性能疏于考虑。本文基于理论分析给出了惯导速度辅助卫导跟踪环路的解决方案，对辅助后环路承载的动态能力，抗干扰性以及对惯导信息精度需求等进行了全方位解析。

图1给出了传统卫导载波跟踪环路结构图。