某型运载火箭一子级动力系统试验尾流辐射场的数值模拟
罗天培,卜 玉,李 茂,刘瑞敏
(北京航天试验技术研究所,北京,100074)
某型运载火箭一子级动力系统试验尾流辐射场的数值模拟
罗天培,卜 玉,李 茂,刘瑞敏
(北京航天试验技术研究所,北京,100074)
采用计算流体力学(CFD)技术,对某型运载火箭动力系统试验时尾流辐射场进行了数值模拟。计算采用氢氧单步燃烧反应模型,标准k-ε 湍流模型获得燃烧流场,同时利用P1辐射模型法考虑热辐射的影响,并引入灰气体加权模型确定气体介质的辐射特性。仿真结果同试验结果进行了对比分析,结果表明,箭体底部的换热方式以辐射换热为主,P1辐射模型可以有效地预测火箭发动机尾流辐射场。
动力系统试验;仿真;辐射;P1辐射模型法
0 引 言
地面试验是液体火箭发动机研制过程中的一个基本环节,通过发动机地面试验可以验证设计的可行性、工艺的可靠性,考核检验调试的方法,对发动机的质量及性能作出评价,而动力系统试验可全面考核火箭子级各发动机工作的协调性、增压输送系统的正确性等[1],对火箭的顺利研制具有重大意义。火箭发动机在进行地面试验时,高温、高速燃气射流会对试验台产生强烈的烧蚀、冲击和辐射作用,为保障人员及试验设施的安全,在试验前对发动机的尾流场进行预估是十分必要的。
美国在战神5运载火箭及航天飞机的研制过程中,分别对燃气射流进行仿真以考察其对试验台及发射场的影响[2,3];中国已对某氢氧发动机的地面试车进行了数值模拟,并提出相关的热防护解决方案[4~6]。
目前,针对发动机尾流场的计算以计算燃烧流场为主,而对于氢氧火箭发动机而言,大部分燃气产物为水蒸汽,并且由于其温度极高(超过3000 K),故辐射在发动机尾流场的传热过程由为重要。
文献[7]表明,火焰中介质的温度很不均匀,其传热对燃烧的流动过程、化学反应过程有很大的影响,也就是说火焰的辐射传热对于燃烧过程本身有强烈的反馈作用。对于试验台的热防护来说,一些设备虽不能直接受到高温燃气的冲刷,但其受到辐射加热的作用不能忽略。
本文对某大型运载火箭动力系统试验尾流辐射场进行数值模拟,并与试验数据进行对比分析,以期得到具有合理精度的仿真模型,并指导试验台的热防护设计。
1 数值计算模型
1.1 几何模型
该动力系统模块采用双发动机并联形式,发动机有初始安装角,试验台井口尺寸为7 m×7 m,箭体底部发动机安装示意如图1所示。

图1 发动机安装示意
动力系统试验时,在箭体底部设置了5个热流密度计,位置分布如图2所示,所用的热流密度计测量的为综合热流,包含辐射热流及对流热流两部分。

图2 热流测点示意
仿真几何模型如图3所示。为节省计算量,经过两次面对称,选取1/4进行计算,计算域尺寸为7 m× 40 m,测点为0.002 m×0.002 m的矩形。对几何模型采用完全结构化网格剖分,射流区域以及热流密度计局部区域进行加密,网格总数约103万。

图3 仿真几何模型
1.2 计算模型
通过求解多组分化学反应雷诺平均、守恒型N-S方程获得燃烧流场,采用双方程标准k-ε模型封闭方程组,源项由氢氧单步燃烧化学动力学模型引入。模型引入重力作用,控制方程采用二阶迎风格式离散,压力和速度采用Simple格式耦合。燃烧流场收敛后,加入P1辐射模型和灰气体加权模型,此时流场内的传热应满足如下[8]方程:式中 keff为有效热导率;Jj为组分j的扩散通量;keff∇T,∑hjJj,τeff·v分别为由于热传导、组分扩散、粘性耗散而引起的能量转移;t,ρ,E,p分别为剪切力、密度、能量及压力;Sh为由辐射引起的热源,可通过求解传输方程得到:
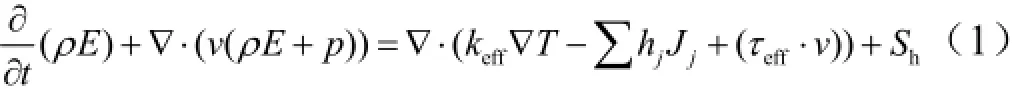

式中 r为位置向量;S为方向向量;S′为散射方向;s为沿程长度(行程长度);a为吸收系数;n为折射系数;σs为散射系数;σ 为斯蒂芬—波尔兹曼常数;I为辐射强度,依赖于位置r与方向S;T为当地温度;Φ为相位函数;Ω′为空间立体角。
该辐射传输方程采用P1辐射模型法求解。P1辐射模型法是一种微分近似的方法,利用球面调和函数将辐射传输方程表示为矩方程,并取球面调和函数的前4项,因此辐射热流qr可由下式得到:
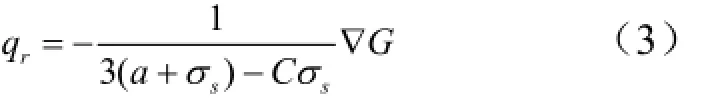
式中 G为入射辐射;C为线性各相异性相位函数系数。
G的输运方程为

联立式(3)和式(4),并将Sh代入式(1),便可将辐射换热引入到温度场的求解中。
对于吸收系数,采用灰气体加权模型确定。该模型将混合气体作为一种单一气体处理,其分布函数通过每一种组分的吸收系数分布函数计算,混合气体的吸收系数为各组分气体吸收系数之和。本文的计算不考虑散射,即散射系数为零。
1.3 边界条件
燃烧室入口采用质量流量入口边界条件,并引入如下假设:假设氢和氧在燃烧室内完全燃烧生成水,这样进入喷管内燃气的成分就只有水和氢,入口温度利用热力计算获得。燃气的基本参数如表1所示。

表 1 燃气的基本参数
在给定入口质量流量、压力和湍流强度等参数,火箭底部及5个测点采用等温壁面边界条件,依据试验数据设为317 K,假设测点全部吸收所投入的辐射,即测点为黑体,发射率取为1;发动机内壁选取绝热壁面条件,外壁采用等温壁面边界条件,根据试验数据,设为850 K,发射率[9]取为0.7;火箭底部旁上边界、流场侧边界及底边界采用压力入口条件,入口压力为1个大气压,组分为空气;对称面采用对称边界条件。
2 计算结果及分析
流场的温度分布及速度分布如图4所示。

图4 尾流场温度及速度分布云图
从图4中可见,射流区域最高温度接近3500 K,由于发动机有初始安装角,燃气射流刚出喷管后向四周发散,速度约为1500 m/s,但随着流动,2台发动机喷出的高速燃气相互影响和引射,燃气射流有向中间靠拢的趋势,到距喷管出口15 m左右的位置,燃气几乎不再向外扩散,流动方向大致沿着火箭的轴向。
对辐射场影响最大的量除了流场的温度分布外,水蒸汽和二氧化碳的分布也起着决定性的作用。流场的水蒸汽和二氧化碳摩尔质量分数分布如图5所示。
由于燃气为富燃状态,燃气从喷管喷出后,剩余约2.2%的氢气和空气中的氧气继续补燃,水蒸汽的分布和流场的温度分布几乎一致。水蒸汽的密度比空气小,但由于燃气速度过快,动能又大,尽管已加载重力模型,但几乎没有水蒸汽向上飘动,火箭底部的辐射场受水蒸汽的影响不大。从图5b中可见,二氧化碳占据了大部分流场上部的区域。

图5 尾流场质量分数分布云图
发动机附近的流线分布如图6所示。

图6 发动机附近流线分布云图
从图6中可见,由于箭体底部燃气的引射,使得大量的空气被抽吸以补充引射形成的低压区,故流场上部二氧化碳的浓度分布和空气中一致,约为0.03%。
流场中气体吸收系数的分布如图7所示。

图7 尾流场吸收系数分布云图
从图7中可见,流场中吸收系数的分布和水蒸汽的分布趋势一致,但扩散的趋势更大,这是由于在水蒸汽射流区域的边缘存在少量的二氧化碳,二氧化碳和水蒸汽对吸收系数有叠加的作用。而流场上部的吸收系数很小,如前文所述,此部分区域内几乎没有水蒸汽,流场上部的气体辐射主要是由空气中少量的二氧化碳造成。
流场上部辐射场(入射辐射)的分布如图8所示。
从图8中可见,喷管火焰引起的辐射受二氧化碳沿程的吸收基本上呈现分层的规律,但是由于二氧化碳本身含量极低,对辐射场的影响相对很小,喷管出口到箭体底部辐射的变化量只占辐射总量的5%左右,也就是说在此区域内的气体辐射热流只占总辐射热流的5%左右。发动机外壁温度850 K,而火箭底部的温度为317 K,由斯忒潘-波尔兹曼定律可知,固体的辐射传热和温度的4次方成正比。同时,由于测点按黑体处理,故箭体底部绝大部分的辐射通量来自于发动机外壁的固体辐射。
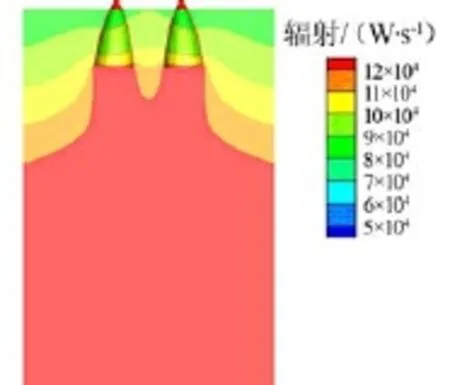
图8 流场上部入射辐射分布云图
表2给出了5个测点辐射热流以及对流热流的分配情况。

表2 辐射热流与对流热流分布情况
从表2中可见,测点1的辐射热流最大,测点5次之,测点2、3、4的辐射热流大体相当;而在对流热流方面,测点5最大,测点1最小,其他3个测点相差不多。
测点1处于两个发动机的中心部位,2台发动机对测点1的角系数互为叠加和补充,故该测点的辐射热流密度值最大,测点5相比测点2、3、4距离发动机更近,从发动机外壁发出的热流受沿程空气的吸收相对较少,故测点5比测点2、3、4的辐射热流略大,而测点2、3、4距发动机距离相当,故辐射热流密度也大体相当。
由图6可知,大部分空气被直接引射到喷管出口,而箭体底部补充进来的空气并不多。箭体底部的速度分布如图9所示。从图9可见,箭体底部有很多1 m/s左右的低速区,这些低速区大部分是由局部的漩涡及气流滞止造成的。测点1处于对称中心的位置,2台发动机从不同方向引射来的气流在此区域会由于对冲而滞止,故此区域的流速最小,测点1的对流热流也就最小,测点3处于一个漩涡的边缘,速度比测点1大,但整体水平依然不高,故测3点的对流换热热流值处于中间位置,而测点5相对于测点1和测点3处于高速区,该点的对流热流最大。

图9 箭体底部速度云图
表3给出了火箭防热底5个测点位置仿真所得到的热流密度数据与试验结果的对比。
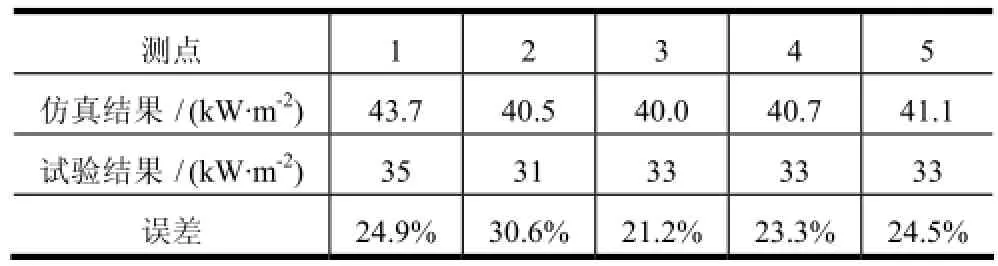
表 3 热流密度仿真结果与试验结果的对比
从表3中可见,5个测点的仿真结果与试验结果的误差最大为30.6%,最小为21.2%,基本上控制在30%以内。
由前文的分析可知,5个测点的热流主要来源为发动机外壁的固体热辐射,发动机外壁温度设为850 K,此温度为发动机外壁的大致平均温度。事实上,喷管的中上部温度略低,接近喷管出口的部分温度较高,而越接近中上部,对5个测点的辐射就越大,故5个测点仿真的结果比试验所测到的值高。
由于本文所用的计算模型基于工程实际考虑,需兼顾计算精度和效率的需求,计算误差主要来源于模型本身,并未考虑全面的燃烧机理及辐射机理。其主要原因是: a)由于采用单步燃烧反应模型,燃烧产物只有水,而实际上还有氢原子、氢氧根等一系列产物,均会对辐射场造成影响;b)P1模型本身基于灰体假设,未考虑气体的光谱选择吸收性,虽然引入灰气体加权模型后会有一定改善,但这种基于试验数据拟合的方法显然会在使用工况不同时存在一定误差。
3 结 论
采用三维对称模型对某型运载火箭动力系统试验中尾流流场及辐射场进行数值模拟,并与试验结果进行了对比分析,结果表明:
a)箭体底部的传热方式以辐射方式为主,而辐射换热以固体辐射为主;
b)氢氧单步燃烧化学动力学模型,配合使用P1辐射模型以及灰气体加权模型(WSGGM)可以有效地预测火箭发动机尾流辐射场。
[1] 郭霄峰. 液体火箭发动机试验[M]. 北京: 宇航出版社, 1990.
[2] Allgood D C, Ahuja V. Computational plume modeling of conceptual ares vehicle stage tests[R]. AIAA 2007-5708, 2007.
[3] Liever P, Radke J, Strutzeberg L, et al. CFD modeling of plume induced environments for space shuttle liftoff debris transport analysis: 2nd Workshop on Lunar and Martian Plume Effects and Mitigation NASA KSC, 2011[C]. 2011.
[4] 李茂, 陈春富, 朱子勇. 架空钢板对火箭发动机试车中地面热载的影响[J]. 导弹与航天运载技术, 2013(2): 41-45.
[5] 李茂, 王占林. 氢氧火箭发动机射流仿真试验台热防护[J]. 载人航天, 2014(20): 421-426.
[6] 李茂, 陈世哲, 陈春富. 火箭发动机地面水平试车尾流温度场仿真分析[J]. 火箭推进, 2012(6): 29-34.
[7] Mustafa I. The effect of thermal radiation and radiation models on hydrogen-hydrocarbon combustion modeling[J]. International Journal of Hydrogen Energy, 2005,30: 1113-1126.
[8] 黄宏艳,王强. 轴对称喷管内外流场与结构温度场耦合计算[J]. 推进技术, 2008(29): 194-199.
[9] 李军伟,刘宇,覃粒子. 二维塞式喷管再生冷却换热的数值模拟[J]. 航空动力学报, 2005(20): 141-153.

图5 设计工作中心测试
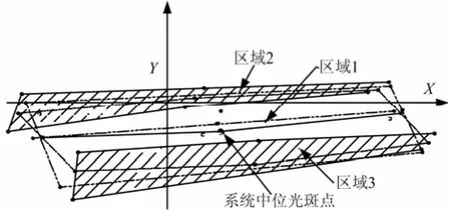
图6 垂直通路光路范围通畅性测试
在集成试验中,上、下仪器共跟踪210次,其间含大风、暴雨、高温、夜间等各种工况,仪器设备工作正常,偏差修正时间不超过5 min,实现了机动快速瞄准。此后,在新一代运载火箭发射场合练及首飞中,瞄准设备均快速准确地实现近距平瞄,静态、动态偏差均在设计计算范围内。
6 结 论
本文通过分析,确定了瞄准上仪器的设计工作位置,采用二次旋转支架实现不同位置的转换,可解决垂直光路遮挡与设计空间有限的矛盾。通过计算,得出架上瞄准设备与箭体棱镜间相对位置变化范围,并将静态偏差指标分配给瞄准支架,以水平和垂直导轨实现,将动态偏差指标分配给瞄准上仪器,由光斑面积覆盖实现。经新一代运载火箭集成试验和发射场试验验证,瞄准设备在无塔架简易发射的环境下,历经各种自然条件均工作正常,瞄准理论工作位置与范围指标合理,该分析方法可作为类似产品设计的参考。
参 考 文 献
[1] 周载学, 等. 发射技术: 上[M]. 北京: 中国宇航出版社, 2009.
[2] 董晓娜. 方位垂直传递技术研究[D]. 北京: 中国科学院, 2001.
[3] 赵宪兵,王新安,杨军等.气象火箭发射装置加工耦合偏差对瞄准精度的影响[J]. 固体火箭, 2007(3): 372-375.
[4] 秦万广, 杨帆, 刘宏. 等精度测量均方根偏差计算方法的讨论[J]. 东北电力学院学报, 2001(9): 27-29.
[5] 闫群, 袁夫彩, 王晓霞. 机械系统精度分配与评价方法的研究[J]. 林业机械与土木设备, 2002(8): 21-23.
[6] 庄夔, 陈明仪,孙麟治,章亚男. 三米丝杠激光动态测量仪总体精度设计[J]. 上海大学学报: 自然科学版, 1995(10): 521-524.
Numerical Investigations of Tail Radiation Fields of a Launch Vehicle First Stage Test
Luo Tian-pei, Bu Yu, Li Mao, Liu Rui-min
(Beijing Institute of Aerospace Testing Technology, Beijing, 100074)
Numerical investigations of a large launch vehicle stage test are conducted by CFD technique. The uni-step H-O reaction model, standard k-ε turbulence model, P1 radiation computation model and the weighted-sum-of-gray-gases model are employed to obtain the flow field. The simulation is evaluated by comparison with the experimental results. The results show that radiation plays magisterial role in heat transfer around the rocket bottom, and P1 radiation computation model can predict the tail radiation fields of the rocket engine effectively.
Launch vehicle stage test; Simulation; Radiation; P1 radiation computation model
V434
A
1004-7182(2016)04-0067-05
10.7654/j.issn.1004-7182.20160417
2015-06-17;
2016-06-23
罗天培(1987-),男,工程师,研究方向为火箭发动机试验技术

