BP神经网络和多元回归方法在乒乓球技战术能力分析中的应用
1.上海体育学院,上海 200438; 2.浙江大学,浙江 杭州 310028
BP神经网络和多元回归方法在乒乓球技战术能力分析中的应用
Application of BP Neural Network and Multiple Regression in Table Tennis Technical and Tactical Ability Analysis
1.上海体育学院,上海 200438; 2.浙江大学,浙江 杭州 310028
杨青1, 张辉2
YANG Qing1, ZHANG Hui2
摘要:运用BP神经网络和多元回归对优秀男子乒乓球运动员的技战术能力进行了分析,结果显示:(1)BP神经网络和多元回归构建的技战术能力模型都具有较高的拟合和预测效能,但BP神经网络在拟合和预测精度上优于多元回归;(2)优秀男子乒乓球运动员第一重要技战术能力为发抢能力,第二重要为发球轮相持能力和接抢能力,接发球轮相持为第四重要能力;(3)乒乓球运动员技战术能力间存在补偿效应,各种技战术水平组合的比赛评定总分大于13分即可获得比赛胜利。
关键词:BP神经网络;多元回归;乒乓球;技战术
BP(Back Propagation)神经网络最早由美国Rumelhart和Mccelland为代表的科学研究小组提出,是一种基于误差反向传播算法训练的多层感知器前馈网络[1]。理论上已证明一个三层BP 网络可以满足一般函数映射的要求,并且用有限隐含层的BP网络可以任意精度逼近任意多变量函数,其自组织、自学习与自适应能力非常突出,体现了人工神经网络中最精华的部分,在实际问题的解决中运用最为广泛[2-9]。多元回归(Multivariate Regression)是统计学中常用的统计工具,它是研究线性相关条件下,两个和两个以上自变量对一个因变量的数量变化关系,表现这一关系的数学公式称为多元回归模型[10]。
技战术能力是乒乓球运动员竞技能力的主导因素[11],围绕着技战术能力进行的科研工作一直是提高乒乓球项目科学化训练的核心内容之一。1989年提出的“三段指标评估法”[12]是乒乓球技战术分析中的经典理论,在乒乓球规则多次改革后,2014年又有“四段指标评估法”[13]提出。本文则根据“四段指标评估法”,运用BP神经网络和多元回归方法分别建立优秀男子乒乓球运动员的技战术能力模型,对这两种模型进行对比分析,探讨最优模型。在此基础上,对不同技战术水平组合下的比赛获胜模式进行探寻,为乒乓球的比赛和训练提供科学依据。
1数据来源及指标选择
1.1数据来源
从国际乒联官方网站和CCTV5官方网站下载观看比赛视频,选取2012-2014年男子世界排名前20位的进攻型打法运动员的单打比赛62场(以2014年3月国际乒联公布的世界排名为准),其中57场用于技战术能力模型的建立,5场比赛用于新样本的预测。
1.2指标及其计算方法
“得分率”是体现乒乓球技战术能力的最优指标,根据乒乓球比赛四段指标评估法[13]的思想,将X1(发抢得分率)、X2(接抢得分率)、X3(发球轮相持得分率,相持I得分率)、X4(接发球轮相持得分率,相持II得分率)作为反映技战术能力的四项指标,同时也是多元回归的自变量和BP神经网络的输入层神经元,比赛结果以“获胜概率”作为因变量和输出层指标。利用Excel对每场比赛的四段得分率和获胜概率进行计算,得分率为段得分与该段得失总分的百分比,获胜概率为场得分与该场比赛得失总分的百分比。
2乒乓球技战术能力模型的建立
2.1BP神经网络模型
BP神经网络模型由输入层、隐含层和输出层组成,隐含层和输出层可以一层或多层构成。训练过程中输入信号从输入层通过作用函数,逐层向隐含层、输出层传播,如果在输出层得不到期望的输出,则转入反向传播,不断修改各层神经元的连接权值,直至使网络输出与期望输出的误差平方和最小,从而训练出最优神经网络模型。
本研究中BP神经网络模型借助于MATLAB2013b的神经网络工具箱实现,采用三层拓扑结构,输入层为X1:发抢得分率;X2:接抢得分率;X3相持I得分率;X4:相持II得分率四个指标,即输入层节点数为4,模型输出层节点数为1,即获胜概率,通过试错法选取隐含层节点数为10。输入层到隐含层采用非线性S函数Tansig 作为训练函数,隐含层到输出层采用线性函数 Purelin 作为传递函数,构成的神经网络模型图见图1。
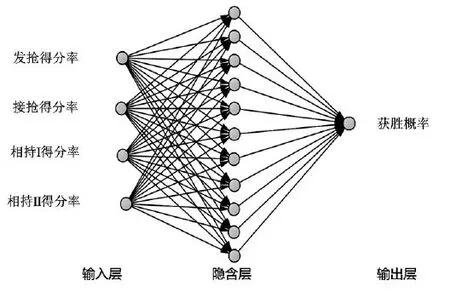
图1 神经网络模型结构
将57场比赛作为训练样本输入,其中随机选择80%用作训练集,10%用作验证集,10%用作测试集,采用工具箱默认的Levenberg-Marquardt算法,网络训练误差图见图2,横轴为训练次数,纵轴为数据集的均方误差,可见经过17次学习后,网络成功收敛,验证集最好均方差达0.000 758 11,训练均方误差达0.000 143 71,表明该网络训练速度快,效果好。
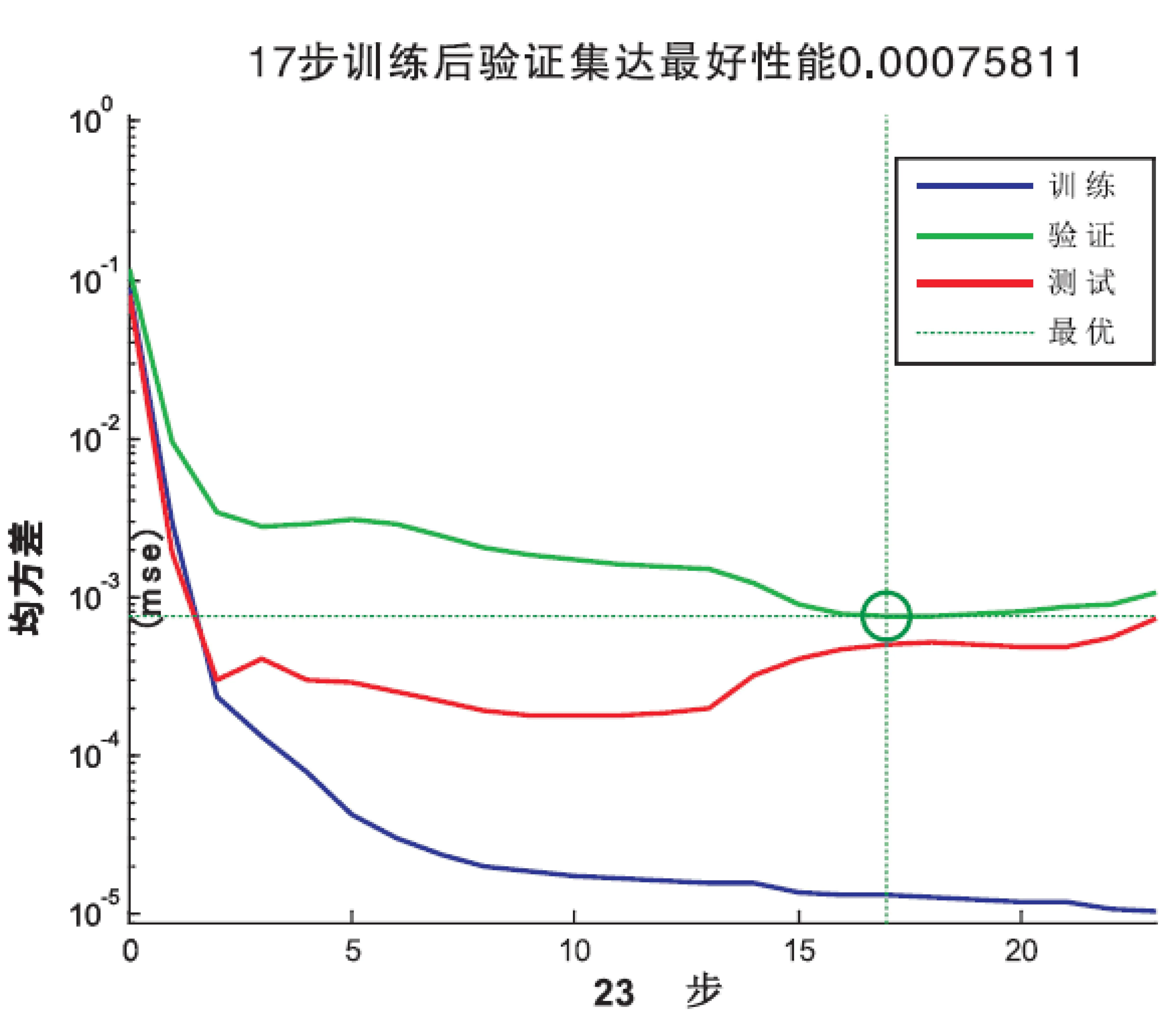
图2训练误差曲线
Figure 2Training error Curves
图3是神经网络模型的拟合回归图,表现输出数据与目标数据直接的相关,由图3可知,训练集、验证集、测试集和整体的拟合值R分别为0.999 11、0.996 97、0.959 07和0.991 7,数据点均匀分布在拟合曲线附近,说明此建立的神经网络模型具有较好的训练效果、预测能力和整体拟合效果。
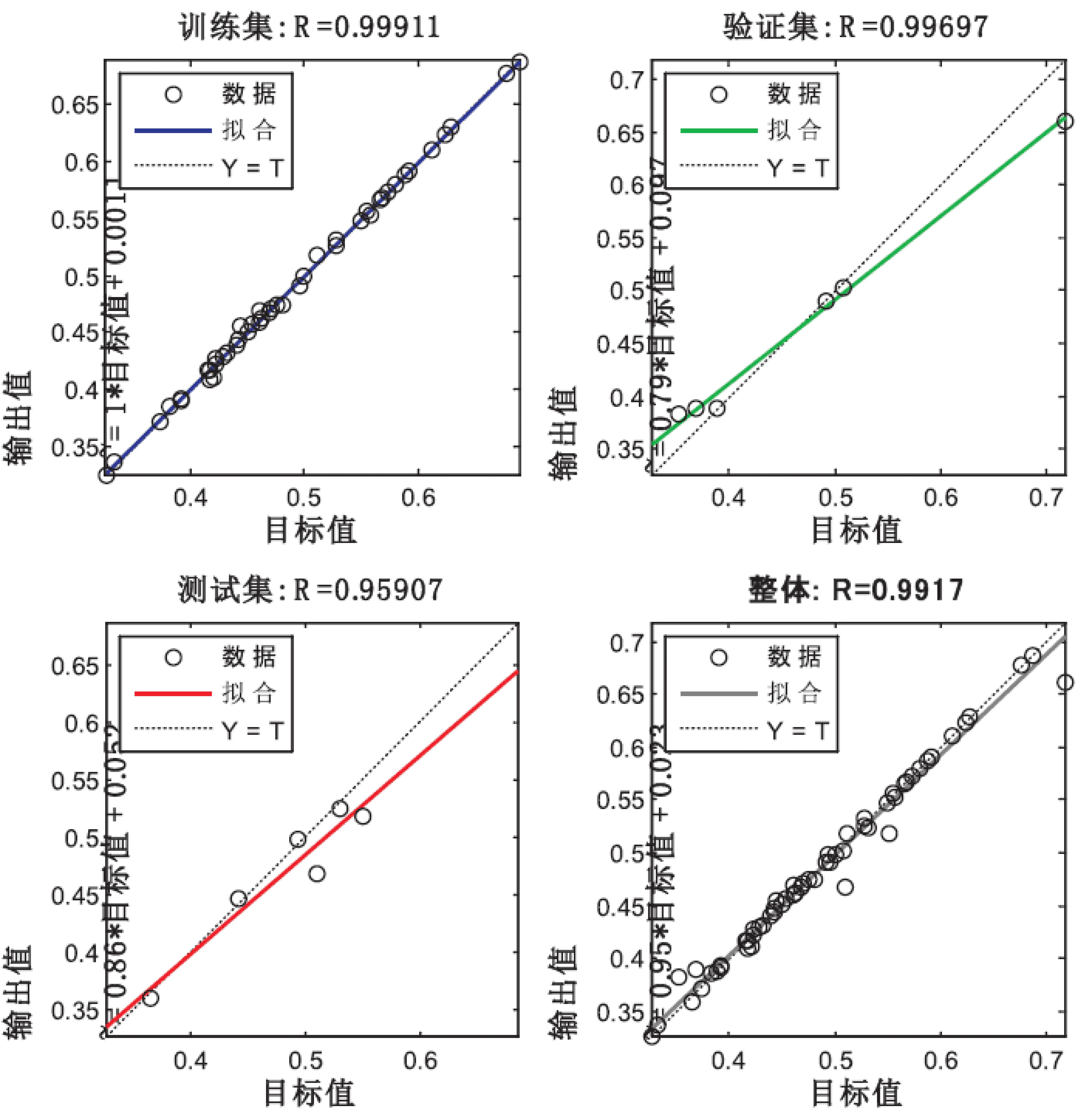
图3神经网络模型拟合回归图
Figure 3Fitting regression of neural network model
2.2多元回归模型
将X1(发抢得分率)、X2(接抢得分率)、X3(相持I得分率)、X4(相持II得分率)作为自变量,Y(获胜概率)作为因变量,由SPSS软件建立多元回归模型,将57场比赛导入软件,方法选择“进入”。

表1 多元回归模型及方差分析结果
根据表1,多元回归模型的复相关系数R,决定系数R2及调整系数R2都在0.97以上,表示模型的拟合度非常好。决定系数R2表示因变量的变异中能够通过回归关系被自变量解释的比例,即模型中四段得分率可解释获胜概率的97.58%。Durbin Waston检验,D值为1.552 2,模型的残差间相互独立。方差分析显示回归模型的F=524.670 2,P<0.01,表明该回归方程具有显著意义。
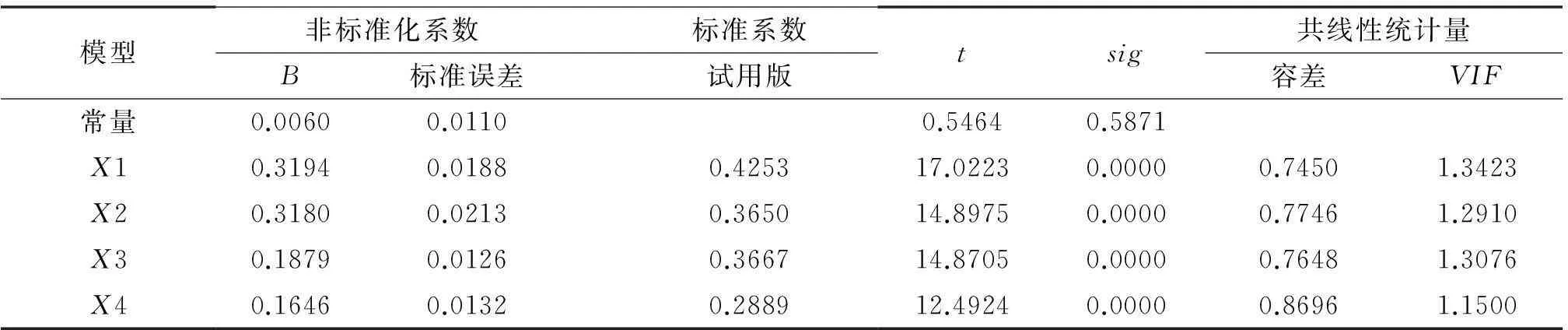
表2 模型系数检验结果
表2显示了多元回归模型系数的检验结果,共线性诊断指标容忍度最小值为0.745 0,方程膨胀因子VIF值均小于2。方程各个自变量t检验的显著性水平值小于0. 01,方程成立,得出优秀男子乒乓球运动员技战术能力的回归模型为:
Y=0.0060+0.3194*X1+0.3180*X2+0.1879*X3+0.1646*X4
多元回归分析结果中给出了模型的偏回归系数和标准回归系数,标准回归系数消除了量纲的影响,可在用来判断自变量对因变量影响的强弱,标准回归系数越大,对因变量的影响作用就越大。故由表2可知,男单比赛中各段技战术能力对比赛获胜概率的影响由大到小依次为:X1发抢得分率>X3相持I得分率≈X2接抢得分率>X4相持II得分率。
2.3两种模型的比较分析
2.3.1拟合精度对比
计算BP神经网络模型的多元回归模型的拟合指标如表3,其中R为复相关系数,它表示模型中的所有变量与因变量之间密切程度大小,取值介于0到1之间,R越大说明线性回归关系越密切。决定系数R2为复相关系数R的平方,值越大,表示模型拟合越好。平均绝对误差为输入数据的模型输出值与实际值绝对差值的平均值,平均相对误差为输出值与实际值的绝对差值占实际值的百分比,均方根误差为输出值与实际值均方误差的平方根,这三个指标值越小表示模型精度越高。表3可以看出两个模型的R都高于0.98,R2均高于0.97,平均绝对误差、平均相对误差和均方根差均较小,说明所建立的两个模型均具有较高的拟合精度,但BP神经网络的各个指标值都要优于多元回归模型,整体拟合精度要高于多元回归模型。

表3 两种模型拟合精度对比
2.3.2预测精度对比
将另外5场比赛带入建立的BP神经网络模型和多元回归模型,得出输出的预测值和实际值的误差、平均绝对误差、平均相对误差和均方根误差如表4所示。

表4 两种模型预测精度对比
表4所示,在5场比赛的预测中,两个模型的误差均较小,但BP神经网络有4场比赛的预测误差都小于多元回归模型(第1、3、4、5场比赛),且从平均绝对误差、平均相对误差和均方根误差上来看,BP神经网络模型分别为0.026 8、6.2929%和0.031 3,多元回归模型则分别为0.032 2、7.3534%和0.034 5,说明两种模型对新样本的预测能力都较好,但BP模型比回归模型更精确。将两种模型的预测值与实际值进行比较(见图4),结果也表明BP神经网络模型新样本的总体预测能力要略高于多元回归。
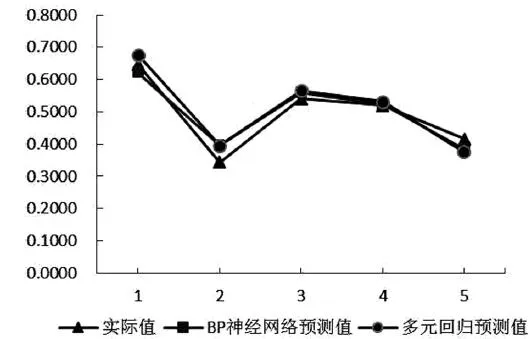
图4 两种模型预测能力比较
通过以上分析可见,建立的两种优秀男子乒乓球运动员技战术能力的模型,BP神经网络和多元回归都表现出了较高的拟合和预测效能,但BP神经网络模型要优于多元回归模型。多元回归模型虽然在模型的精度上不如BP神经网络模型,但在建立模型进行分析的同时,可依据标准回归系数对各个自变量对因变量的重要程度进行判断,得到更多因素间的相互关系信息,将这两种方法结合使用会得到更好的效果。
3不同技战术水平组合比赛的模拟分析
四段指标评估法[13]将乒乓球比赛四段的得分率按照评估标准分了优、良、中、差四个等级,现用多元回归和BP神经网络模拟四个不同等级的技战术能力相互组合的比赛情况。四段技战术能力,每段四个等级,则根据排列公式,可有256种不同的排列,将每个评估标准的下限值(评估为“差”的指标值取0)作为自变量和输入层指标带入已建立的多元回归和BP神经网络模型,输出结果即为256场不同技战术水平组合比赛的最低获胜概率,部分数据仿真结果见表5。
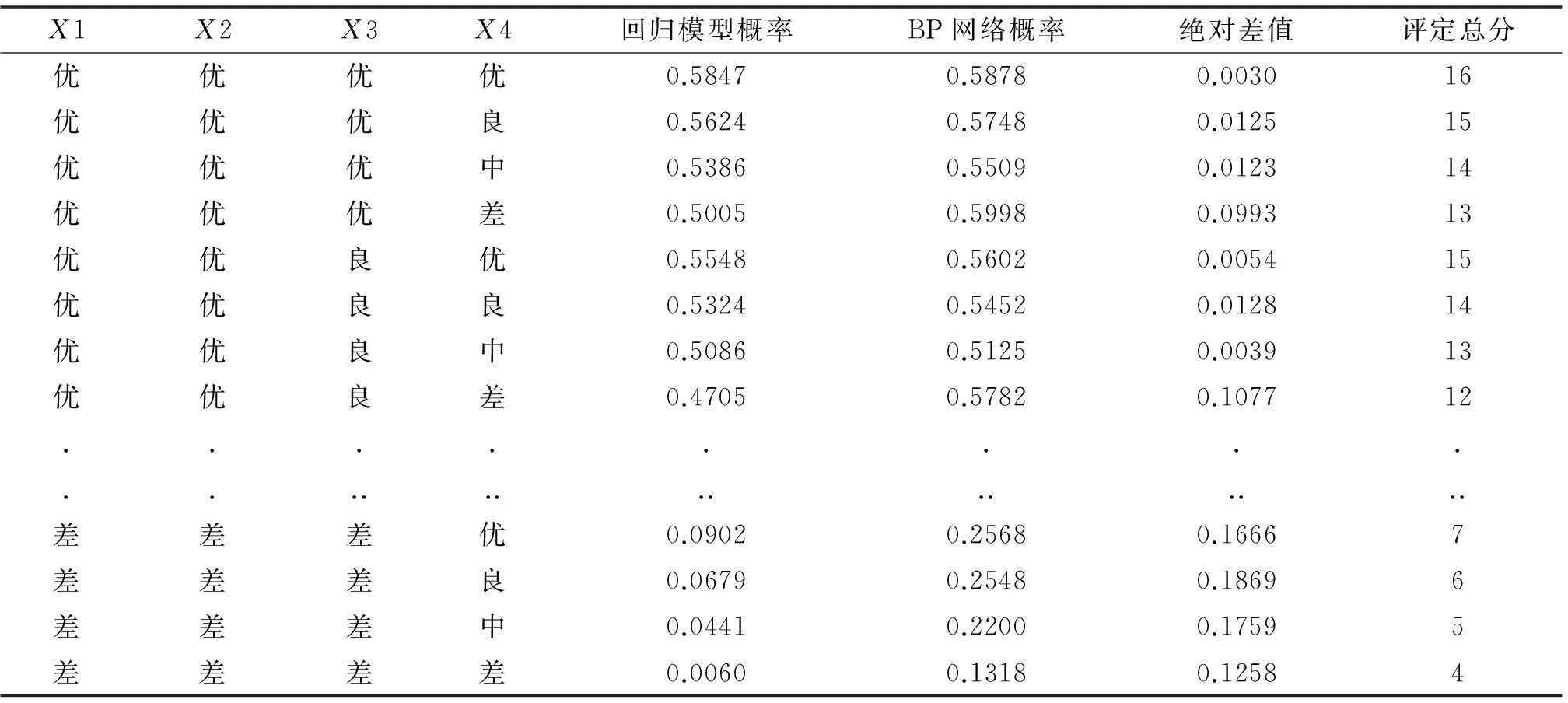
表5 部分数据仿真情况一览
注:设将优、良、中、差分别赋值为4、3、2、1分,表中“评定总分”为该场比赛四项指标的评分之和。
根据表5,两种方法仿真后所得的获胜概率差别较小,平均绝对差值为0.064 3。以0.5为标准,将获胜概率在0.5及以上组合模式的比赛结果视为获胜,低于0.5视为落败,将BP神经网络和多元回归预测获胜结果不一致(即BP神经网络预测为获胜而多元回归预测为失败,或BP神经网络预测为失败而多元回归预测为获胜)的组合模式的结果视为“胜负难测”,比赛中“胜负难测”的组合模式有18种,对此18种“胜负难测”的组合模式不予考虑。根据对其他238种组合模式的分析可发现:(1)乒乓球各项技战术能力间存在补偿效应,某一技战术能力的薄弱可由其他较强的技战术能力得到补偿,即某一技战术能力发挥较差,而其他技战术水平发挥优异则仍可获得比赛胜利,这种补偿效应因技战术能力的类型和等级有所不同。(2)如将四段技战术能力按照优良中差的评估标准分别给予4、3、2、1分的赋值,那么评定总分13分是男子运动员单打比赛划分胜负的分水岭,当评定总分高于13分时即可获得比赛胜利,低于13分则会落败。当评定总分等于13分时,“三优一差”组合(“优-优-优-差”除外)和“中-优-良-优”组合会落败,其他组合均可获胜。应注意的是,本文探讨的是不同技战术水平组合下比赛的最低获胜概率,故判断为失败的比赛在实践中有获胜的可能性。
4结论
(1)BP神经网络和多元回归建立的优秀男子乒乓球运动员技战术能力模型都具有较高的拟合和预测效能,但BP神经网络模型的精度要高于多元回归模型,而多元回归则能更好地揭示各个自变量对因变量的重要程度,建议将这两种方法结合使用,相互验证,优势互补。
(2)优秀男子乒乓球运动员第一重要技战术能力是发抢,第二重要是发球轮相持能力和接抢能力,第四是接发球轮相持能力。
(3)乒乓球技战术能力间存在补偿效应,这种补偿效应因技战术能力的类型和等级有所不同。男子运动员单打比赛中各种技战术水平组合的比赛评定总分大于13分即可获得比赛胜利,低于13分落败。
参考文献
[1]韩力群.人工神经网络教程. [M].北京:北京邮电大学出版社,2006:58.
[2]张文阳,张良均,李娜,等. 多元回归和BP人工神经网络在预测混合厌氧消化产气量过程中的应用比较 [J]. 环境工程学报, 2013, 7(2): 747-752.
[3]吕丹. 基于BP神经网络的同龄林林木资源资产批量评估模型研究[D]. 江西:江西农业大学,2014.
[4]孙文兵,曾祥燕,杨立君. BP 网络和多元回归在葡萄酒质量模型中的应用[J]. 计算机工程与应用,2014,50(15):267-270.
[5]苏玉玲,刘雯,田波,等. 基于人工神经网络的碱性蛋白酶水解乳清蛋白预测模型的建立[J].食品工业科技,2014,35(7):100-103.
[6]王颖林,赖芨宇,郭丰敏. 建设需求量预测分析中的人工神经网络和多元回归方法[J].武汉工程大学学报,2013,35(11): 77-80;86.
[7]肖毅,张辉. 中国乒乓球队奥运攻关研究报告——基于人工神经网络的乒乓球比赛诊断模型研究[J].体育科研,2008,29(6):19-22.
[8]赵昀. 丁宁乒乓球比赛中组合技术模拟分析[C].上海:2013年全国体育计算机应用学术会议,2013:272-276.
[9]赵永寿. 关于构建铅球运动员成绩的人工神经网络预测模型的研究[J]. 北京体育大学学报,2006,29(4):486-488.
[10]何晓群. 多元统计分析(第2版) [M].北京: 中国人民大学出版社,2008.
[11]田麦久.运动训练学[M].北京:人民体育出版社,2000:22.
[12]吴焕群,李振彪.乒乓球比赛中实力与技术诊断的方法及其应用效果[J].国家体委科学研究所学报,1989(1):32-41.
[13]杨青,张辉.乒乓球比赛技战术“四段指标评估法”的构建与应用[J]. 天津体育学院学报,2014,29(5):439-442.
Abstract
Using BP neural network and multiple regression, this study analyzed the technical and tactical ability of elite male table tennis players. Results show that: (1) The models based on both BP neural network and multiple regression are highly efficient in fitting and forecasting. The BP neural network-based model performs better than the multiple regression-based model in both aspects; (2) The primary technical and tactical ability of elite male players is their attack-after-service ability, and the second their rallying ability and receiving and blocking ability in serving rounds, the fourth their rallying ability in multiple rounds of serving and returning; (3) There is a compensation effect between table tennis technical and tactical abilities. In a match featuring different technical and tactical levels, a total score of over 13 points means the game is over.
Key words:BP Neural Network; Multiple Regression; Table Tennis; Technique and Tactics
CLC number:G846Document code:AArticle ID:1001-9154(2016)01-0078-05
(编辑孙君志)
中图分类号:G846
文献标志码:A
文章编号:1001-9154(2016)01-0078-05
收稿日期:2015-07-28
作者简介:杨青,在读博士研究生,研究方向:乒乓球训练理论与方法,E-mail: yangqing4520@163.com。
1. Shanghai University of Sport, Shanghai 200438; 2.Zhejiang University, Hangzhou Zhejiang 310028

