原油调度优化中的分段线性松弛研究

周 祥，周智菊，吕 宁，郭锦标

(中国石化石油化工科学研究院，北京 100083)

原油调度优化中的分段线性松弛研究

周 祥，周智菊，吕 宁，郭锦标

(中国石化石油化工科学研究院，北京 100083)

针对混合原油性质计算导致原油调度优化模型中出现非线性约束并严重影响模型求解性能的情况，采用分段线性松弛法将非线性约束转化为线性形式，使模型可应对原油多次混合的复杂情况。以实际炼油厂的原油调度优化为例，对混合原油硫含量计算作线性转化，并将分段线性松弛法与两种常见方法的应用效果进行了对比。计算结果表明：分段线性松弛法可使模型的求解性能达到工业应用要求；当加工油种的硫质量分数为0.50%～3.00%时，分段线性松弛法更有利于获得优化的调度方案；当加工油种硫质量分数的差异由0.50%增加至2.50%时，分段线性松弛法对厂区罐内混合原油硫含量的计算值均接近实际值，相对偏差低于5%，可确保模型的准确度满足工业应用要求。

原油调度 优化模型 分段线性松弛 硫含量

国内炼油厂加工的原油品种较多、性质差异较大，多油种混炼是操作常态，并时常掺炼劣质原油和机会原油以提高效益，因此原油调合越来越受到炼油厂重视，成为其加工过程的第一道工序。原油调度优化可提供合理的原油调合操作方案，保障蒸馏装置及后续装置的平稳运行并缓解库存压力[1]。利用数学模型实现原油调度优化具有可行性[2-7]，然而实际原油储运过程比较复杂，期间一般发生多次原油混合，使混合原油的性质计算呈非线性，模型中存在此类约束时会严重影响其求解性能[3-5]。

求解含非线性约束的原油调度优化模型多采用迭代法[6-7]，此方法的求解效率取决于迭代初值的设置是否合理，而调整初值主要依靠调度人员的经验，自动化程度较低。约束规划建模方法可允许模型中出现较多的非线性约束[5]，其优势在于快速获得可行的调度方案，模型中一旦设置优化目标则求解效率同样较低。本课题采用分段线性松弛法将模型中混合原油性质的计算转化为线性形式，并与两种常见的处理方法进行比较，考察线性松弛对模型求解性能及准确度的影响。

1 非线性约束转化

1.1 非线性约束

沿海炼油厂的原油储运流程较长，原油调合操作复杂，其原油调度优化问题具有代表性。图1为沿海炼油厂原油调度过程示意。由图1可知，沿海炼油厂的原油调度需考虑油轮到港卸油、码头罐收油、原油经长输管线付至厂区罐、厂区罐向蒸馏装置供料的全过程。一般而言，各品种的原油在码头罐内单储以便于收付计量，多个码头罐付油到长输管线时发生原油的第一次混合，厂区罐接收多段由长输管线送来的混合原油时发生第二次混合，国内炼油厂多在蒸馏装置进料环节进行劣质原油和机会原油的掺炼，即存在多个厂区罐同时向一套蒸馏装置供料的情况，这将导致第三次原油混合。

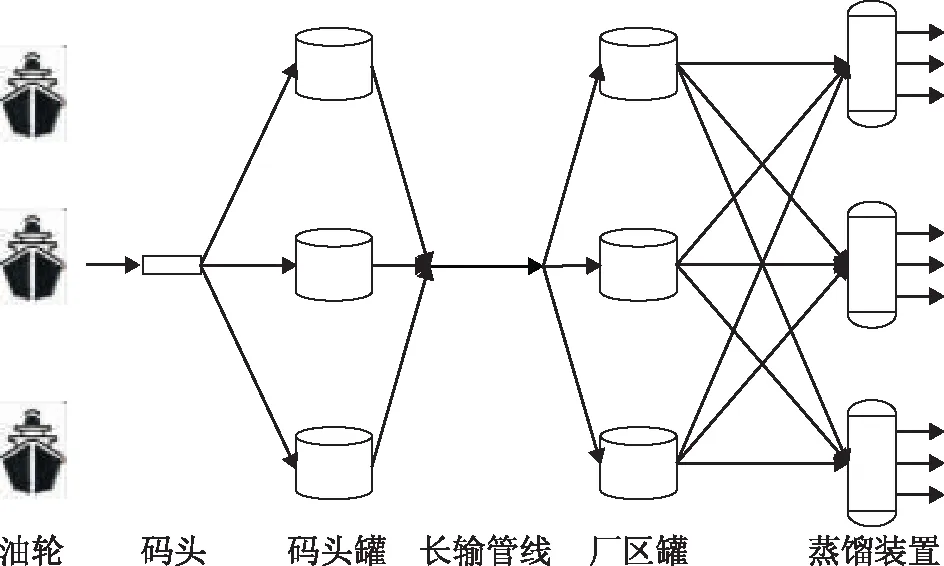
图1 沿海炼油厂原油调度过程示意

原油调度优化的主要目的是确保厂区罐所存混合原油的性质满足蒸馏装置进料要求，并尽可能减少进料性质波动。Lee等[3]将硫等影响混合原油性质的因素定义为“关键组分”，直接对这些“关键组分”在厂区罐内的存量进行物料衡算，通过限制厂区罐向蒸馏装置供应“关键组分”的数量来满足蒸馏装置的进料性质要求，如式(1)和式(2)所示。

WT,S=WT,S,0+WT,S,I-WT,S,O

(1)

(2)

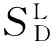
式(1)和式(2)均呈线性，而实际上厂区罐供给蒸馏装置的是混合原油，其中所含“关键组分”的数量受厂区罐内混合原油性质的约束，如式(3)所示。

WT,S,O=WT,O·ST

(3)

式中：WT，O为厂区罐付出混合原油的质量，t；ST为厂区罐内混合原油的硫质量分数，%。

厂区罐内原油二次混合的情况在沿海炼油厂的储运过程中普遍存在，厂区罐从长输管线接收“关键组分”的数量可表示为式(4)。

WT,S,I=∑(WP,O·SP)

(4)

式中：WP，O为长输管线付出混合原油的质量，t；SP为长输管线付出混合原油的硫质量分数，%。

式(3)和式(4)均呈非线性，导致原油调度优化模型中出现非线性约束，而劣质原油和机会原油的掺炼将使模型中的非线性约束进一步增加。

1.2 分段线性松弛法

“关键组分”法为保障模型的求解效率，回避了式(3)和式(4)所示的非线性约束[3]，然而求解模型所获得的调度方案中，厂区罐内的混合原油性质及蒸馏装置的进料性质与实际情况往往存在较大的偏差，严重时会导致方案不具备可操作性。

由式(3)和式(4)可知，模型中的非线性约束均具有双线性形式(bilinear)。有研究者提出将此类双线性约束转化为一系列线性约束，这种处理方法会使模型中的约束更松弛，因此松弛模型的最优解可能不同于原模型(松弛模型的最优解通常更加优化)。然而，松弛模型不包含非线性约束，其求解效率大大高于原模型，若能减小松弛模型与原模型的差异，则其优化解的准确性亦有保证[8-9]。以前的研究曾尝试利用Convex and Concave Envelopes(简称CCE)法实现非线性约束的线性转化[10]，但此方法对双线性约束的松弛不够紧致，且国内炼油厂所加工原油的性质差异较大，因此对混合原油性质的计算也存在较大的偏差。

为实现更为紧致的线性松弛，本研究对双线性约束中变量的取值区间进行划分，并据此对变量乘积作分段松弛。以式(3)所示双线性约束为例，将厂区罐内混合原油硫含量的取值区间均分为N段，各段端点值如式(5)所示。

(5)

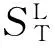
(6)

(7)

从厂区罐向蒸馏装置的供料量与蒸馏装置的加工量相关联，在实际操作中蒸馏装置的加工量一般比较稳定，因此对供料量的取值区间进行分段意义不大。定义变量ΔWT，O，n，与硫含量各子区间相对应，当BT，S，n= 1时ΔWT，O，n为供料量相对其下限值的偏差，以式(8)和式(9)约束。

(8)

(9)

对式(3)进行线性松弛，如式(10)～式(13)所示。

(10)

(11)

(12)

(13)

由式(10)～式(13)可知，当N= 1时，此分段线性松弛法与CCE法是等效的，而不同之处在于，此方法为使线性松弛更紧致而在模型中引入了新的01变量，增加01变量也可能会降低模型的求解效率。目前，混合整数线性规划模型求解算法和软件工具的开发比非线性规划模型更为完善，对于大规模工业应用级的模型，其优势更加明显，因此01变量对模型求解性能的影响弱于非线性约束，而调整N的取值也可平衡松弛紧致程度和01变量数。

2 计算结果与讨论

2.1 案例介绍

以某沿海炼油厂的原油调度优化为案例，考察线性松弛对模型求解性能及准确度的影响。该炼油厂以含硫和高硫原油为主要加工油种，储运系统包括1个油轮停靠泊位、10个码头罐、1条长输管线、8个厂区罐，原油在厂区罐内进行二次混合，有时在蒸馏装置进料环节掺炼劣质原油和机会原油。

以180 h为一个调度周期，采用异步连续时间模式建立该炼油厂的原油调度优化模型，综合考虑油轮滞船期、蒸馏装置进料性质波动及储罐收付切换次数等指标，并以其加权和最小为优化目标[10]。蒸馏装置的进料性质要求重点考虑硫含量指标，并选择不同的初始状态使调度周期内加工油种的硫含量位于不同的区间。为比较模型的求解性能及准确度，分别应用“关键组分”法、CCE法与上文所述分段线性松弛法对模型进行转化，在分段线性松弛法中对混合原油硫含量划分10个子区间(N= 10)。

2.2 模型规模及求解性能

模型的求解环境为：32个主频为2.8 GHz的CPU核心、128 G内存、64位XPRESS 7.5混合整数线性规划求解器。表1为3种方法所得模型的规模(均为预求解后)，其中“关键组分”法忽略了非线性约束，因此所得模型规模最小；CCE法并未使模型中增加新的变量，而是将非线性约束松弛化使模型中的约束增加；分段线性松弛法最为复杂，使模型规模明显扩大，尤其是01变量增加了60%以上。

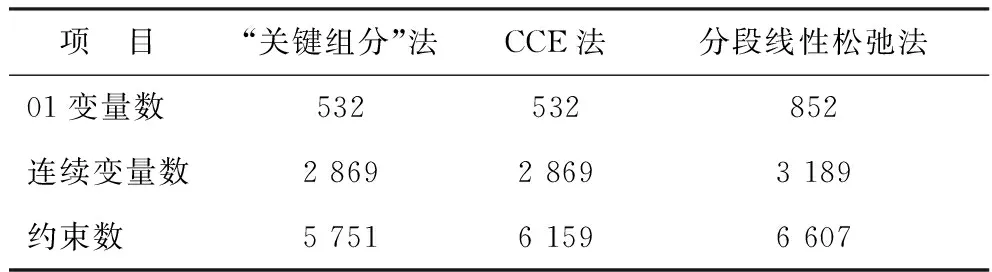
表1 3种方法所得模型的规模

当加工油种的硫含量位于不同区间时，3种方法所得模型的求解情况如表2所示。工业应用对模型的求解效率有较高的要求，因此将模型求解时间上限设为1 h，若求解时间达到上限时仍未获得最优解，则记录当前优化解，若在求解时间上限之前获得最优解，则记录计算时间和最优解。

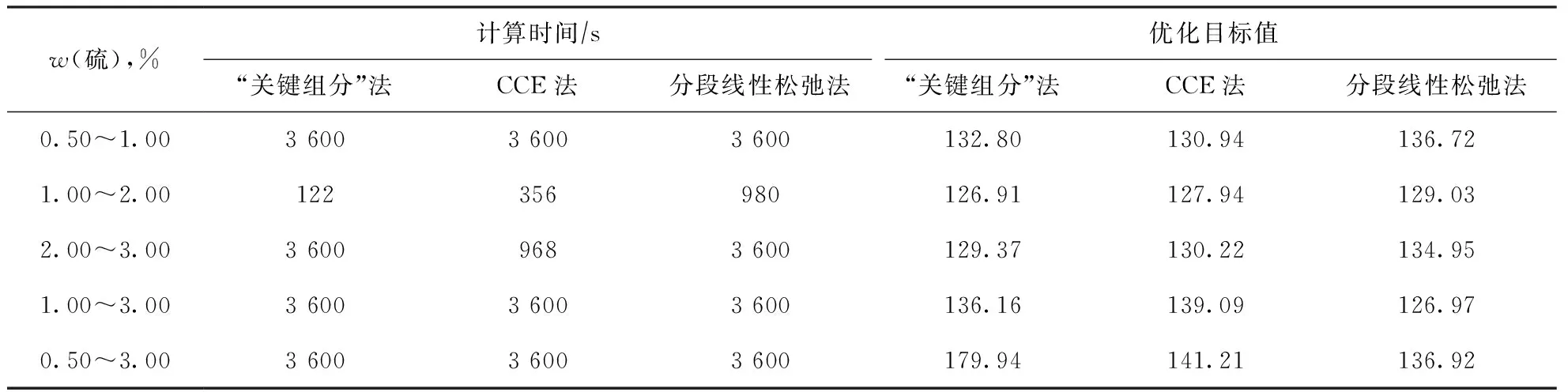
表2 3种方法所得模型的求解情况

由表2可知：3种方法所得模型均可在1 h内获得优化解，求解性能均满足工业应用要求；当加工油种的硫质量分数差异较小时(≤1.00%)，“关键组分”法和CCE法所得模型的求解效率更高，较易确定最优解，然而当加工油种的硫质量分数位于2.00%～3.00%时，CCE法已确定最优方案的优化目标值不低于130，而“关键组分”法则已将最优目标值降至130以下，可见后者获得的优化调度方案未必可靠；当加工油种的硫质量分数差异较大时(>1.00%)，“关键组分”法和CCE法所得模型的求解效率下降，达到求解时间上限时优化目标值相对较差；分段线性松弛法所得模型也可确定最优解，同时其求解效率对加工油种硫含量的差异不敏感，而且当差异较大时，应用此方法在相同计算时间内获得的优化解质量最好，表明其具有更广泛的适用性。

此外，虽然分段线性松弛使模型中的01变量大幅增加，但模型的求解性能仍然较好，其原因在于01变量的取值是通过分支定界算法确定的，分支定界过程在求解环境内以并行计算的方式完成，从而缓和了01变量规模对模型求解效率的影响。

2.3 模型准确度

准确计算混合原油的性质需采用非线性约束，而线性松弛法将式(3)和式(4)中的非线性等式约束转化为线性不等式约束，因此可能导致混合原油性质的计算值与实际值之间存在偏差。为考察模型的准确度，对应用3种方法获得的优化调度方案进行验算，依据方案中各加工油种的储运过程确定厂区罐内混合原油硫含量的实际值，将计算值与实际值进行比较，最大相对偏差(|计算值-实际值|/实际值×100%)如表3所示。

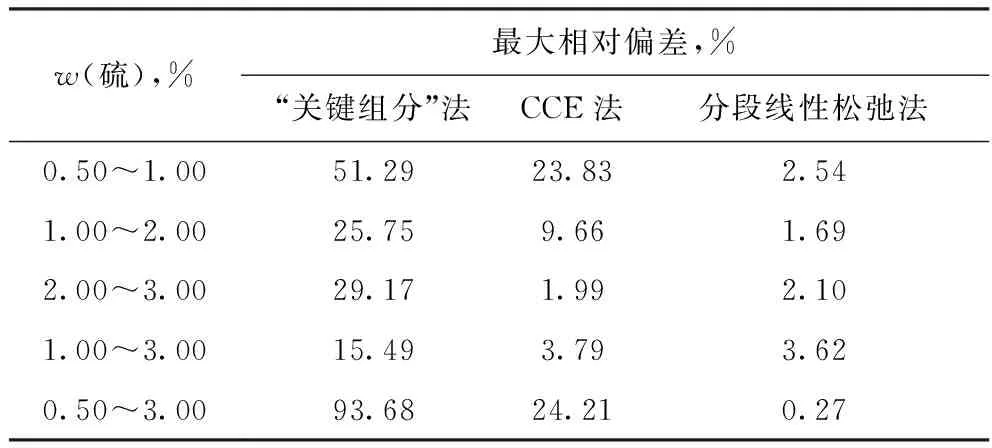
表3 3种方法所得模型计算厂区罐混合原油硫含量的准确度

由表3可知：“关键组分”法所得模型的准确度较差，当加工油种的硫质量分数差异较小(0.50%～1.00 %)或较大(0.50%～3.00%)时，其计算偏差可能达50%以上，这是忽略混合原油性质计算造成的影响，应用此方法获得的调度方案不具备可操作性；CCE法所得模型的准确度高于“关键组分”法，然而其计算偏差同样受限于加工油种硫含量的差异；与CCE法相比，分段线性松弛法对混合原油性质计算进行了更为紧致的转化，因此所得模型的准确度在3种方法中是最高的，并且当加工油种的硫含量位于不同区间时，计算偏差均在5%以下，可满足工业应用要求，获得的调度方案具备可操作性。

3 结 论

采用分段线性松弛法将混合原油性质计算转化为线性形式，避免原油调度优化模型中出现非线性约束，适用于炼油厂掺炼劣质原油和机会原油的复杂情况。以实际炼油厂的原油调度优化为例，对混合原油硫含量计算作线性转化，将分段线性松弛法与两种常见方法的应用效果进行了对比，计算结果表明：应用分段线性松弛法可使模型的求解性能达到工业应用要求；当加工油种的硫质量分数为0.50%～3.00%时，分段线性松弛法更有利于获得优化的调度方案，具有更广泛的适用性；当加工油种硫质量分数的差异由0.50%增至2.50%时，分段线性松弛法始终能将厂区罐内混合原油硫含量的计算偏差控制在5%以下，确保模型的准确度满足工业应用要求，所获得的调度方案具备可操作性。

[1] 郭锦标，杨明诗.化工生产计划与调度的优化[M].北京：化学工业出版社，2006：163-165

[2] Shah N.Mathematical programming techniques for crude oil scheduling[J].Computers & Chemical Engineering，1996，20(S)：1227-1232

[3] Lee H，Pinto J M，Grossmann I E，et al.Mix-integer linear programming model for refinery short-term scheduling of crude oil unloading with inventory management[J].Industrial & Engineering Chemistry Research，1996，35(5)：1630-1641

[4] Jia Z，Ierapetritou M G，Kelly J D.Refinery short-term scheduling using continuous time formulation：Crude oil operations[J].Industrial & Engineering Chemistry Research，2003，42(13)：3085-3097

[5] 周祥，郭锦标，周涵，等.原油混输调度的模型法研究[J].石油炼制与化工，2008，39(1)：49-52

[6] Li Wenkai，Hui Chiwai，Hua Ben，et al.Scheduling crude oil unloading，storage，and processing[J].Industrial & Engineering Chemistry Research.2002，41(26)：6723-6734

[7] Reddy P C P，Karimi I A，Srinivasan R.Novel solution approach for optimizing crude oil operations[J].AIChE Journal，2004，50(6)：1177-1197

[8] Meyer C A，Floudas C A.Global optimization of a combinatorially complex generalized pooling problem[J].AIChE Journal,2006，52(3)：1027-1037

[9] Karuppiah R，Grossmann I E.Global optimization for the synthesis of integrated water systems in chemical processes[J].Computers & Chemical Engineering.2006，30(4)：650-673

[10]周智菊，周祥，郭锦标，等.基于异步时间段的连续时间原油混输调度模型[J].石油炼制与化工，2015，46(6)：96-101

STUDY ON PIECEWISE LINEAR RELAXATION FOR CRUDE SCHEDULING OPTIMIZATION

Zhou Xiang，Zhou Zhiju，Lü Ning，Guo Jinbiao

(SINOPECResearchInstituteofPetroleumProcessing，Beijing100083)

The efficiency of solving crude scheduling optimization models is seriously affected by nonlinear constraints，which are produced by the property calculations of mixed crudes. In order to empower the model to cope with multiple crude pooling situations，a piecewise linear relaxation approach was employed to convert the nonlinear constraints into linear ones. Crude scheduling optimization of a real refinery was used as an example and the sulfur content calculations of mixed crudes were converted into linear forms. The effect of the piecewise linear relaxation approach was compared with another two frequently-used approaches. The results indicated that by use of the piecewise linear relaxation approach，the efficiency of solving the converted model met industrial application demand；while the sulfur contents of the processed crudes lied between 0.50% and 3.00%，the piecewise linear relaxation approach was more conducive to acquire optimal scheduling schemes；as the sulfur content difference of the processed crudes increased from 0.50% to 2.50%，the calculated sulfur contents of mixed crudes in charging tanks remained close to the actual value with the piecewise linear relaxation approach，the relative deviations were under 5% and therefore the industrial demand for model accuracy was satisfied.

crude scheduling；optimization model；piecewise linear relaxation；sulfur content

2016-02-15；修改稿收到日期：2016-04-19。

周祥，博士，主要研究方向为炼油过程模型及炼油企业调度优化。

周祥，E-mail：zhoux.ripp@sinopec.com。