基于纵横交叉算法的神经网络配电网故障选线研究
孟安波,葛佳菲,李德强,翁子豪,焦夏楠
基于纵横交叉算法的神经网络配电网故障选线研究
孟安波,葛佳菲,李德强,翁子豪,焦夏楠
(广东工业大学,广东 广州 510006)
为了提高小电流接地系统单相接地故障选线的精度,提出一种基于纵横交叉算法优化RBF神经网络的故障选线新方法。利用Matlab/Simulink仿真单相接地得到一组零序电流信号,通过小波包变换和傅里叶变换从中提取出暂态特征值、有功分量以及五次谐波分量。再将提取得到的特征量作为神经网络的输入,用纵横交叉算法优化后的神经网络对故障特征值进行训练,实现故障选线。仿真中建立100组不同的故障样本,其中80组作为训练集,20组作为测试集。实验结果表明,与传统神经网络相比,CSO-RBF方法训练效果好,准确性高。
小波包变换;纵横交叉法;输电线路故障诊断;RBF神经网络;局部最优
0 引言
小电流接地系统是我国中低压配电网的主要运行方式,而其中单相接地故障是占故障比例最大的[1]。由于发生单相接地时,故障特征信号不明显,因此小电流接地系统的单相接地故障选线问题一直没有得到彻底解决[2-3]。对此,国内外许多学者都做了大量的研究工作,可总结为两方面的改进:(1) 利用信号处理方法提取出特征参数;(2) 用算法或者其他选线模型提高选线精确度。如文献[4]提出了基于粗糙集理论的故障选线方式,应用了粗糙集理论的数据挖掘能力,先增强采样的零序电流信号,再用小波包对采样信号进行分析。文献[5]提出了基于蚁群算法的神经网络故障选线方法,将蚁群算法和多层前馈神经网络融合,克服了神经网络训练时间长和容易陷入局部最优的缺点。文献[6]提出了基于接地故障电流无功和有功分量解耦补偿的电磁混合消弧及对地参数测量方法,利用逆变器的等效负阻特性,提高故障线路动态零序导纳对MCR调节量的灵敏度,进而提高故障选线精度。
鉴于已有的研究成果,本文提出一种基于纵横交叉算法优化RBF神经网络的故障选线新方法。该方法首先用小波包变换和傅里叶变换对零序电流信号进行特征参数提取,再用纵横交叉算法优化RBF神经网络,提高网络的泛化能力和训练精确度,通过训练得到选线结果。
1 纵横交叉算法
纵横交叉算法(Crisscross Optimization Algorithm,CSO)[7]是受儒家思想和遗传学思想启发产生的新算法,其搜索行为主要包括横向交叉和纵向交叉两个主要算子。
1.1 横向交叉
横向交叉是种群中同一维的两个不同粒子间的算术交叉,交叉前先对粒子进行两两随机配对,假设父代粒子X (i)和X (j)的第d维进行横向交叉,则它们的子代可表示为
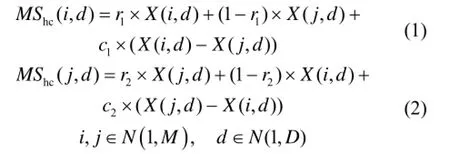
式中:c1、c2是介于(-1,1)之间的随机数;r1、r2是介于(0,1)之间的随机数;D是变量的维数;M是粒子的规模;X (i,d)、X (j,d) 分别是父代粒子X (i)和X (j)的第d维;MShc(i, d) 和MShc(j,d)分别是X (i,d)和X (j,d)通过横向交叉产生的第d维子代。
从式(1)和式(2)可以看出,MShc(i,d) 和MShc(j,d)是父代个体X(i,d)、X(j,d)在高维超立方体空间的新解,横向交叉以较大概率在超立方体内产生子代,同时也会以小概率跳出父代包含空间范围,在立方体外缘进行搜索,从而减少搜索盲点。
1.2 纵向交叉
纵向交叉是所有粒子维度层面的交叉计算,由于不同维之间的取值可能不同,因此交叉前要对各维粒子进行归一化处理。假定粒子X (i)的第d1维和第d2维进行纵向交叉,可表示为
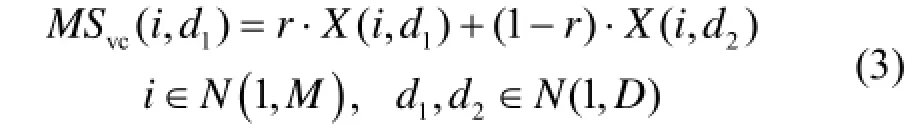
两种交叉方式的有机结合不仅加速了种群的收敛速度,个体一旦陷入停滞不前的某维,粒子会在纵向交叉操作下摆脱局部最优,并通过横向交叉操作迅速传播至整个种群,而更新后的维也会使其余陷入局部最优的维有更多机会通过纵向交叉跳出局部最优,两种交叉方式的结果会呈链式反应在整个种群中蔓延。相比其它群智能优化算法,这种纵横交叉机制使得 CSO在全局收敛能力和收敛速度方面具有明显的优势。
2 纵横交叉算法优化RBF神经网络
2.1 RBF神经网络
RBF神经网络是一个由输入层、隐含层和输出层组成的前馈神经网络[8]。它的基本思想是用径向基函数作为隐单元的“基”,由此构成隐含层空间。隐含层将低维模式输入的数据变换到高维空间内,使得低维空间内的线性不可分问题在高维空间内可分[9]。RBF神经网络结构图如图1所示。
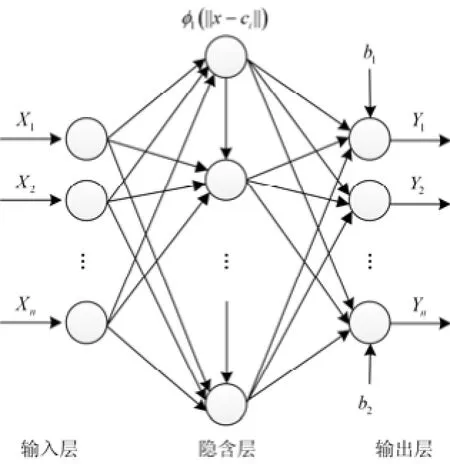
图1 RBF神经网络结构图Fig. 1 Neural network structure of RBF
2.2 纵横交叉算法优化RBF神经网络
RBF网络的性能决定于网络基函数的中心和方差以及权值。由于CSO算法具有全局搜索能力强的特点,为克服神经网络固有缺点提供了可能。将CSO优化RBF神经网络可以提高神经网络的收敛速度以及泛化能力,同时在训练时能优化网络的链接结构、减少冗余链接从而提高网络训练的准确性。
1) 建立RBF神经网络,设置基本参数和误差函数。
2) 初始化种群,设置纵横交叉的基本参数,包括:种群规模,最大迭代次数,惯性权重,纵向交叉概率。
3) 设置适应度函数,对群体中每个个体进行适应度评价,用如下均方误差公式(适应度函数)衡量每个粒子的适应度值。
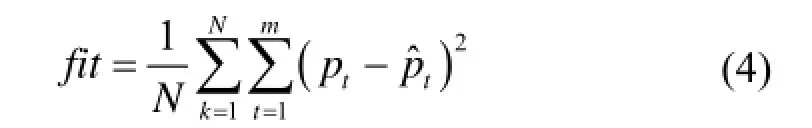
式中:pt、分别是神经网络的实际输出和目标输出;N为训练样本数。
4) 横向交叉:将种群内粒子两两配对,每对粒子通过式子(1)和(2)进行横向交叉,产生一对中庸解保存在矩阵 MShc然后计算 MShc中每个解的适应值,与父代种群进行比较,适应度更好的保留在矩阵X中。
5) 纵向交叉:对种群所有粒子进行归一化处理,再对同一粒子的所有维进行随机配对,在交叉概率为 Pv下选取一定数量的维,通过式子(3)进行交叉产生子代,反归一化后与横向交叉更新后的X进行比较,择优保留在矩阵X中。
6) 迭代次数加1,是否达到结束条件(迭代次数和最小误差要求),如果达到,停止迭代,输出适应度最好的参数,否则转移到第3步进行新一轮迭代。
3 基于纵横交叉算法的配电网故障选线
3.1 小波包变换与快速傅里叶变换
由于发生故障时零序电流特征信号不明显,因此分别用小波包变换(Wavelet Packet Transform, WPT)[10]和快速傅里叶变换(Fast Fourier Transform, FFT)[11]从零序电流中提取出暂态分量、五次谐波分量和有功分量。
3.1.1 小波包变换
小波分析适合对非平稳信号进行处理,而小波包分解(Wavelet Packet Decomposition ,WPD)[12]是在小波变换的基础上产生的。小波分解每次只对低频部分进行再分解,没有对高频分量进一步的剖分,这种固定的分解方式对不同的分解目的而言不一定能达到最佳效果。而小波包分解能同时在同一级尺度上对低频和高频部分机型分解,形成一个完整二叉树结构,分解得到 2j个子序列,j为分解层数,也就是尺度数。
3.1.2 快速傅里叶变换
快速傅里叶变换(FFT),是离散傅里叶变换(DFT)的快速算法,是根据DFT的虚、实、奇、偶等特性,对其进行改进而得[13]。
在对信号进行变换时,可以将其看成两个变量得x, y函数。引入二维连续函数的傅里叶变换,设f(x, y)的两个变量相互独立,且满足则定义
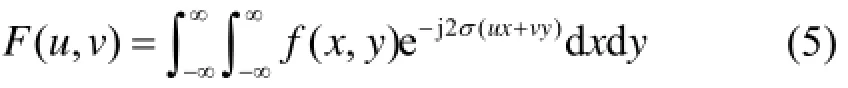
为f(x, y)的傅里叶变换。定义
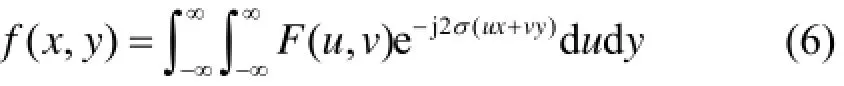
为傅里叶反变换。而傅里叶变换的振幅普、相位谱和能量谱分别为
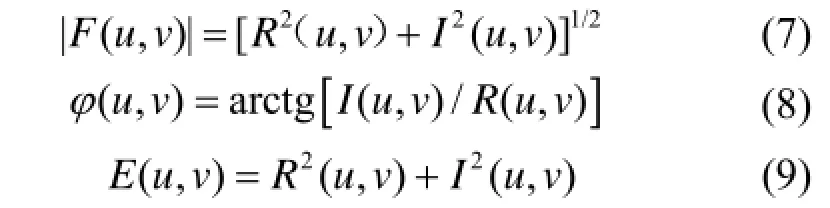
式中,R,I分别表示傅里叶变换的实部和虚部。将连续信号经过抽样后变成二维离散信号 (,)f m n,相应地定义二维离散傅里叶变换(DCT)及其反变换为
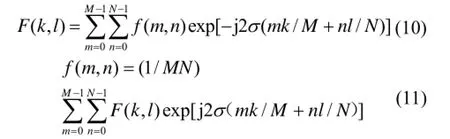
3.2 故障特征提取
3.2.1 暂态分量
当配电网小电流接地系统发生单相接地故障时,线路零序电流的暂态分量能量较大,而稳定分量的能量相对较小,由于小波包分析能对非平稳信号进行精确分析,还能对信号的低频及高频部分进行分解,因此可用小波包变换对暂态分量进行特征值提取,实现故障选线。
3.2.2 有功分量
在中性点经消弧线圈接地系统中,发生单相接地时线路的零序电流有功分量远大于非故障线路,其等于各线路零序电力有功分量和消弧线圈电流有功分量之和,且方向相反。利用这一特性,通过快速傅里叶变换提取出有功分量,如式(12)所示。

式中:kP为线路k零序电路的有功功率;På为配电网中所有线路零序电流的有功功率总和。
3.2.3 五次谐波分量
中性点经消弧线圈接地系统中的消弧线圈是按照基波整定的,所以消弧线圈对高次谐波产生的补偿效果可忽略。因此可以通过零序电流五次谐波比相法解决选线问题[14],通过快速傅里叶变换可以从零序电流中提取五次谐波分量。五次谐波式子如式(13)。

式中:5KS 表示第 k条线路的零序电流谐波分量的是在功率;5Så表示电网所有线路零序电流五次谐波分量的是在功率总和。
3.3 基于纵横交叉算法的选线模型
1) 分别用小波包变换和快速傅里叶变换从零序电流中提取出暂态分量、五次谐波分量和有功分量。
2) 以暂态分量、五次谐波分量和有功分量作为训练样本集和测试样本集的输入量。
3) 初始化神经网络参数,建立CSO-RBF神经网络模型。
4) 对神经网络进行训练,得到选线结果。具体流程如图2所示。
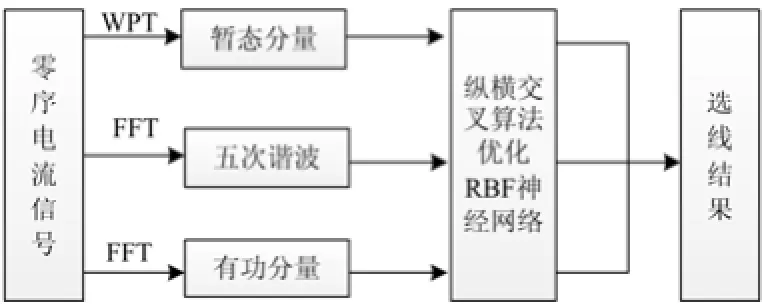
图2 基于纵横交叉算法的故障选线模型Fig. 2 Fault line selection model of CSO-RBF
4 实验仿真
4.1 仿真模型
用Matlab/Simulink搭建仿真模型,系统仿真模型如图 3所示。该系统为一个有 4条线路的 110 kV/10 kV小电流接地系统。其中,4条线路长度分别是L1=8 km,L2=12 km,L3=15 km,L4=20 km。零序电感为 3.9146 mH/km,正序电感为 1.1705 μF/km,零序电容为0.036 μF/km,正序电容为0.062 μF/km,零序电阻为0.7 W/km,正序电阻为0.45 W /km。
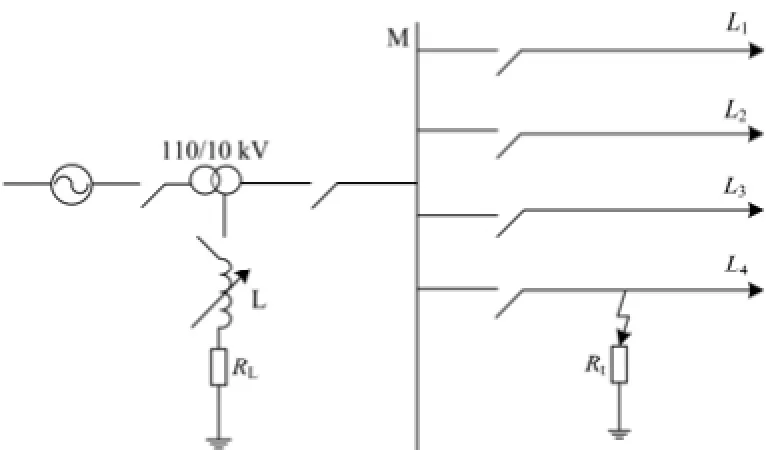
图3 系统仿真模型Fig. 3 System model of simulation
4.2 输入层、隐含层以及输出层设置
4.2.1 输入和输出层设置
分别取4条线路零序电流的暂态分量e、五次谐波分量S和有功分量P作为系统某一故障的特征输入量,向量表示如下所示。
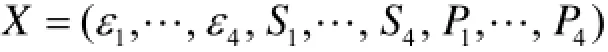
式中,输入层节点数为12,选择要判断故障的线路或母线作为输出,向量表示如下。
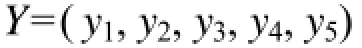
式中:y1至y4为4条线路的状态;y5为母线状态。
4.2.2 隐含层节点数选择
神经网络隐含层节点数的选择对网络训练有很大影响,节点数太少会导致网络学习能力欠佳,节点数过多会增加网络复杂性,导致训练易陷入局部最优。而神经网络隐含层节点数的选取比较复杂,目前没有公认的标准解析式[15]。一般隐含层节点数跟输入层和输出层节点数有关系,可采用以下经验公式。
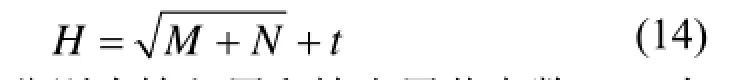
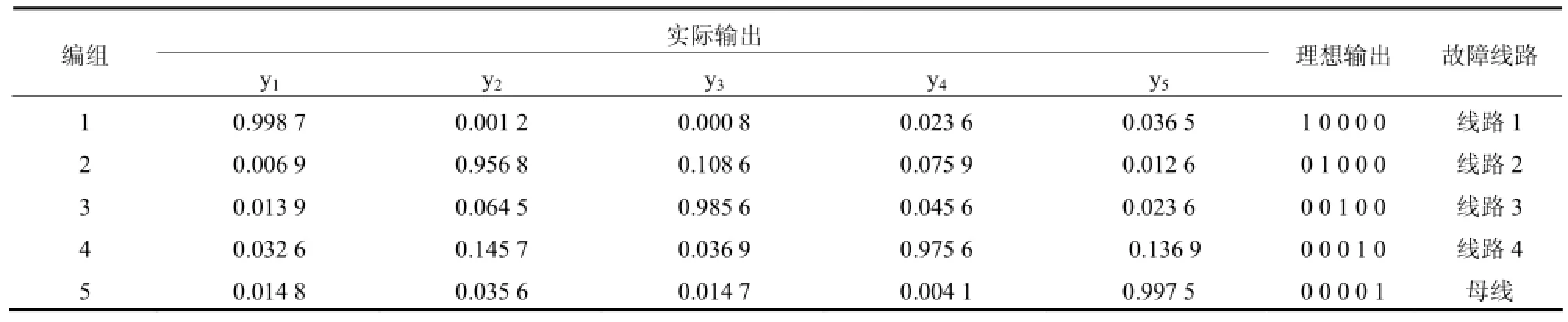
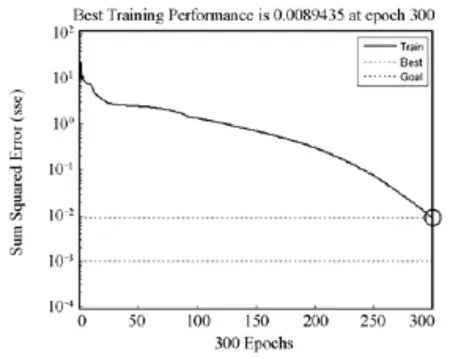
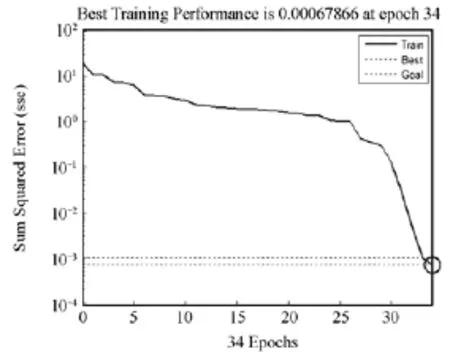
式中:M,N分别为输入层和输出层节点数;H为隐含层节点数;t(1 4.3 仿真设置 4.3.1 样本处理 用Matlab仿真得到各线路的零序电流,通过小波包分解和快速傅里叶变换得到暂态分量、五次谐波分量以及有功分量。为了得到更多的故障样本,仿真时设置不同的故障条件:1) 改变故障点距离,每条线路长度的20%、50%、80%;2) 改变故障线路;3) 改变故障角,分别为0º、45º、90º;4) 改变接地电阻,分别为0 W、50 W、500 W。 4.3.2 参数设置 神经网络中,输入层、隐含层、输出层节点数分别为12、8、5。训练代数为300;学习速率为0.1;目标误差为0.001。CSO参数设置:解空间维数D为 480,种群大小为 50,最大迭代次数,CSO中,PVC设为0.5。 4.4 实验结果 本文通过仿真得到不同状态下的100组样本,取其中的80组作为学习样本,另外的20组作为测试样本。为了验证本文方法有效性,分别用RBF神经网络和CSO-RBF进行对比。表1为RBF测试结果,表2为CSO-RBF测试结果,由于篇幅问题,只显示其中的5组输出结果。 对表1和表2分析可知,未经处理的RBF神经网络实际输出值与理想输出有一定差距,而且在第二组数据中出现了错误。这是由于神经网络容易出现学习过渡,陷入局部最优以及泛化能力差等特点,导致训练结果欠佳。而CSO优化的RBF神经网络,大大提高神经网络的泛化能力和训练精确性,使输出值很好地逼近实际值,有效提高网络的训练准确性。 由图4和图5分析可知,未经优化的神经网络在前期收敛较快,但在中期由于陷入局部最优,导致训练停滞不前,缓慢更新。而纵横交叉算法结合了横向寻优和纵向变异的强大择优能力,使神经网络表现出良好的泛化能力和超高的精确度。从图 5可以看出CSO-RBF前期收敛速度较慢,从25代以后开始快速收敛,而且一直趋向高精度。由此可见,CSO-RBF模型适用于配电网的故障选线。 表1 RBF神经网络测试样本输出Table 1 Test sample output of RBF network 表2 CSO-RBF测试样本输出Table 2 Test sample output of CSO-RBF 图4 RBF神经网络误差曲线Fig. 4 RBF training error curve 图5 CSO-RBF神经网络误差曲线Fig. 5 CSO-RBF training error curve 配电网出现小电流单相接地时,特征信号不明显,选线问题复杂,用一般方法难以达到选线要求。对此,本文将各线路零序电流信号通过小波包和快速傅里叶变换提取出暂态特征值、有功分量以及五次谐波分量,从而充分反映故障信号的特征。再将提取出的故障特征量作为神经网络输入量,鉴于传统神经网络训练能力的不足,本文用CSO优化后的RBF神经网络进行训练。通过实验仿真和分析对比可知,CSO优化后的RBF神经网络收敛速度快,训练精度高,能有效提高配电网故障选线的准确性。 [1] 赖平, 周想凌, 邱丹. 小电流接地系统暂态电流频率特性分析及故障选线方法研究[J]. 电力系统保护与控制, 2015, 43(4): 51-57. LAI Ping, ZHOU Xiangling, QIU Dan. Research on transient-current frequency analysis and faulty line detecting method in indirectly grounding power system[J]. Power System Protection and Control, 2015, 43(4): 51-57. [2] 王韶, 朱姜峰. 基于改进相关性分析法的配电网络单相接地故障选线[J]. 电力系统保护与控制, 2012, 40(15): 76-81. WANG Shao, ZHU Jiangfeng. Faulty line selection of single-phase to ground fault in distribution network basedon improved correlation analysis method[J]. Power System Protection and Control, 2012, 40(15): 76-81. [3] 司瑞琦, 黄翰, 罗建, 等. 基于消弧线圈补偿特征的故障选线新方法[J]. 电力系统保护与控制, 2014, 42(23): 16-22. SI Ruiqi, HUANG Han, LUO Jian, et al. Fault line selection approach based on compensation characteristics of extinction coil[J]. Power System Protection and Control, 2014, 42(23): 16-22. [4] 庞清乐, 孙同景, 钟麦英. 基于粗糙集理论的配电网故障选线装置研究[J]. 高电压技术, 2007, 33(3): 37-41. PANG Qingle, SUN Tongjing, ZHONG Maiying. Research on fault line detection device for distribution networks based on the rough set theory[J]. High Voltage Engineering, 2007, 33(3): 37-41. [5] 李容, 任睿, 宋聚忠. 在配电网中发生单相接地故障时不借助电压互感器计算残余电压角度的方法[J]. 电力系统保护与控制, 2015, 43(4): 143-149. LI Rong, REN Rui, SONG Juzhong. A method to compute residual voltage angle without voltage transformers during single phase earth fault in distribution network[J]. Power System Protection and Control, 2015, 43(4): 143-149. [6] 王朋, 田翠华, 陈柏超, 等. 基于新型磁控消弧线圈的电磁混合消弧及配合选线新方法[J]. 电工技术学报, 2015, 30(16): 175-183. WANG Peng, TIAN Cuihua, CHEN Baichao, et al. Electromagnetic hybrid arc suppression and a novel method of feeder selection based on the novel magnetic controlled petersen coil[J]. Transactions of China Electrotechnical Society. 2015, 30(16): 175-183. [7] MENG Anbo, CHEN Yuchen, YIN Hao. Crisscross optimization algorithm and its application[J]. Knowledgebased System, 2014, 67: 218-229. [8] 岳恒, 张海军, 柴天佑. 基于混合粒子群算法的 RBF神经网络参数优化[J]. 控制工程, 2006, 13(6): 525-529. YUE Heng, ZHANG Haijun, CHAI Tianyou. Strategic study of RBF neural network parameter optimization[J]. Control Engineering of China, 2006, 13(6): 525-529. [9] 夏轩, 许伟明. 改进的粒子群算法对 RBF神经网络的优化[J]. 计算机工程与应用, 2012, 48(5): 37-40. XIA Xuan, XU Weiming. Improved particle swarm optimization on RBF neural networks[J]. Computer Engineering and Applications, 2012, 48(5): 37-40. [10] 张淑清, 马跃, 李盼, 等. 基于改进的广义谐波小波包分解和混沌振子的小电流接地系统故障选线[J]. 电工技术学报, 2015, 30(3): 13-20, 43. ZHANG Shuqing, MA Yue, LI Pan, et al. Application of improved generalized harmonic wavelet packet decomposition and chaos oscillator to fault line detection in small current grounding system[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 13-20, 43. [11] 赵峰, 尹德昌. 小波包与改进BP神经网络的配电网故障选线[J]. 自动化仪表, 2013, 34(9): 4-8. ZHAO Feng, YIN Dechang. Fault line selection based on wavelet packet and improved BP neural network for power distribution grid[J]. Process Automation Instrumentation, 2013, 34(9): 4-8. [12] 陈盼, 陈皓勇, 叶荣, 等. 基于小波包和支持向量回归的风速预测[J]. 电网技术, 2011, 31(5): 177-182. CHEN Pan, CHEN Haoyong, YE Rong, et al. Wind speed forecasting based on combination of wavelet packet analysis with support vector regression[J]. Power System Technology, 2011, 35(5): 177-182. [13] 杨丽娟, 张白桦, 叶旭桢. 快速傅里叶变换 FFT及其应用[J]. 光电工程, 2004(增刊1): 1-3. YANG Lijuan, ZHANG Baiye, YE Xuzhen. Fast Fourier transform and its applications[J]. Opto-Electronic Engineering, 2004(S1): 1-3. [14] 金涛, 褚福亮. 基于暂态非工频零序电流的含 DG新型配电网的接地选线方法[J]. 电工技术学报, 2015, 30(17): 96-105. JIN Tao, CHU Fuliang. A fault line-selection method in new distribution network with DG based on transient non-power frequency zero sequence current[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 96-105. [15] 冯华丽, 刘渊, 陈冬. QPSO算法优化BP网络的网络流量预测[J]. 计算机工程与应用, 2012, 48(3): 102-104. FENG Huali, LIU Yuan, CHEN Dong. Network traffic prediction based on BPNN optimized by QPSO algorithm[J]. Computer Engineering and Applications, 2012, 48(3): 102-104. (编辑 张爱琴) Research on fault line selection of distribution network using RBF neural network based on crisscross optimization algorithm optimization MENG Anbo, GE Jiafei, LI Deqiang, WENG Zihao, JIAO Xianan In order to improve the precision of single phase to earth fault line selection device for the small current grounding system, an improved fault line detection method using RBF neural network based on crisscross optimization algorithm (CSO) optimization is presented. By means of Matlab/Simulink, numerous single-phase-to-earth fault experiments are carried out and many zero sequence current signals are obtained. The fault characteristics of the zero sequence current signals, such as transient characteristic value, active component and five harmonic component, are extracted by wavelet packet transform and Fourier transform. Then choosing the extracted characteristic quantity as the input of neural network, using neural network which has been optimized by CSO to train fault characteristic value, the fault line selection can be realized. Through the simulation, 100 sets of different fault samples are set up, and the 80 groups are set as training sets, and the 20 group is the test set. The simulation results indicate that compared with the traditional neural network, the proposed method has better training effect and higher precision. wavelet packet transform; crisscross optimization algorithm; transmission line fault diagnosis; RBF neural network; local optimum 2015-10-26; 2016-01-27 孟安波(1971),男,博士,副教授,主要研究方向为电力 系 统 自 动 化 、 系 统 分 析 与 集 成 ;E-mail: menganbo@vip.sina.com 葛佳菲(1991-),男,通信作者,硕士研究生,研究方向为电力系统运行、智能电网;E-mail: 479542427@qq.com 李德强(1991-),男,硕士研究生,研究方向为电力系统运行、智能电网。E-mail: 928752686@qq.com 10.7667/PSPC151888 广东省电网公司科技项目(GDKJ00000009)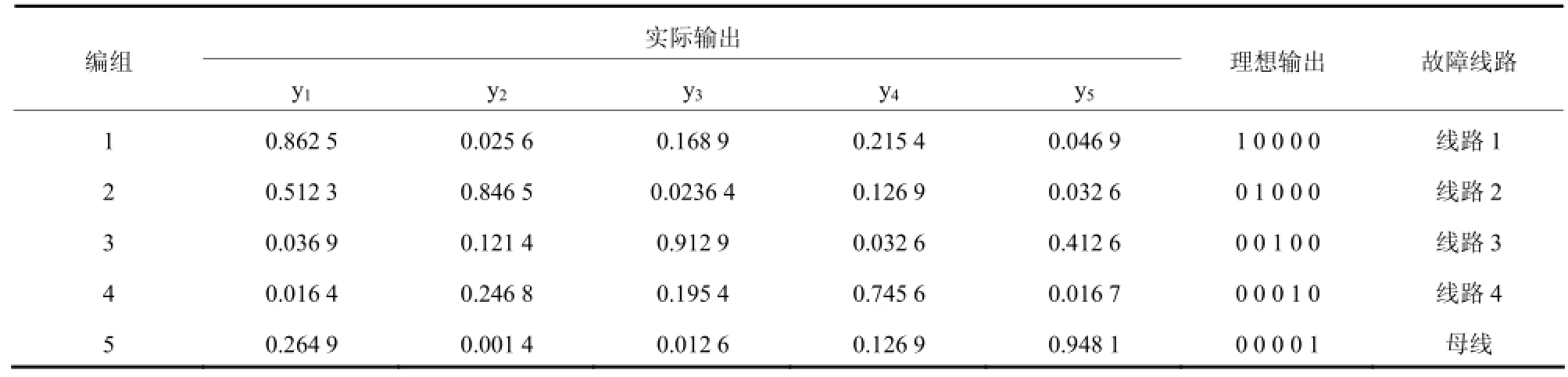
5 总结
(Guangzhou University of Technology, Guangzhou 510006, China)

