整车质量目标设定与分解研究

高新华 ,　涂少平,　王其东

(1.合肥工业大学 机械与汽车工程学院, 安徽 合肥　230009; 2.奇瑞汽车有限公司 汽车工程研究总院,安徽 芜湖　241009)



整车质量目标设定与分解研究

高新华1,2,涂少平2,王其东1

(1.合肥工业大学 机械与汽车工程学院, 安徽 合肥230009; 2.奇瑞汽车有限公司 汽车工程研究总院,安徽 芜湖241009)

摘要:文章就整车质量目标的设定与分解方法进行了研究,通过多元回归分析结果和一元回归分析结果的对比,确定影响整车质量的主要参数,然后根据一元回归分析得出主要参数和整车质量之间的关系式,从而达到设定整车质量目标的目的,同时采取比值分析法对整车质量目标进行分解。

关键词:质量目标;多元回归法;一元回归法;比值分析法

在当前汽车技术的发展中,轻量化技术的应用水平已经成为衡量汽车技术水平和产品开发水平的重要标志之一,目前我国自主品牌轿车的质量比同级别合资品牌的车型平均要重8%~10%[1]。汽车轻量化是实现汽车节油和降低排放的最有效途径之一。据统计,轿车质量每减轻10%,可节油7%~8%,排放减低4%[2]。国内专家学者对轿车轻量化技术的研究主要集中在2个方面:轻量化材料的使用和轻量化的结构设计[3-10],这2个方面的研究成果非常多,但是在整车质量目标制定与分解方面的研究很少。

本文着重寻找影响整车质量的主要参数,并利用该主要参数,通过回归分析,对新开发车型的整车质量进行设定,并对设定的整车质量目标进行分解。

1线性回归分析预测法

整车质量的变化取决于多个因素的变化情况,这些因素有主次之分,有时几个影响因素主次难以区分,或者有的因素虽属次要,但也不能略去其作用。因此,对整车质量目标的设定一般可采用多元回归分析预测法。

多元回归分析预测法中,当整车质量与影响因素之间存在线性关系时,称为多元线性回归分析。建立多元线性回归模型时,为了保证回归模型具有优良的解释能力和预测效果,应首先注意影响因素的选择,其准则如下:

(1) 影响因素对整车质量有显著的影响,且两者呈密切的线性相关。

(2) 影响因素与整车质量之间的线性相关不是形式上的,而是真实的。

(3) 影响因素之间应具有一定的互斥性,即影响因素之间的相关程度不应高于影响因素与整车质量之间的相关程度。

(4) 影响因素应具有完整的统计数据,其预测值容易确定。

多元线性回归模型的参数估计是在要求误差平方和为最小的前提下,用最小二乘法求解模型参数。多元线性回归模型在得到参数的最小二乘法的估计值后,一般需要对线性回归方程进行必要的检验与评价,以决定线性回归方程是否可以应用于整车质量目标的设定。

线性回归方程的拟合程度可用相关性指数R2来表征,它是在影响因素的总变化中,由线性回归方程解释的变动(回归平方和)所占的比重。R2的计算公式为:

(1)

计算得到的R2越大,说明线性回归方程拟合各对样本数据点的程度越强,影响因素与整车质量之间的线性关系越密切。

2整车质量目标的设定

整车质量目标设定的依据来源于竞争车型质量数据库,因此竞争车型的选择非常关键。选择竞争车型需要按照以下原则:

(1) 轴距与目标车型轴距相差±50 mm。

(2) 投产年份小于等于5 a。

(3) 碰撞星级在同一碰撞标准下与目标车型的星级相同。

(4) 排量与目标车型相同。

(5) 配置与目标车型基本相同。

(6) 制造商方面，选择自主、韩日和欧美各车型的数量基本一致。

在满足这些条件的前提下,所选择的车型数量越多,目标设定的结果越准确。在进行回归分析时,需选择竞争车型的相关参数。由于事先不太了解有关参数与整车质量之间的关系,可以选择若干可能的参数,研究其与整车质量之间的关系。

按照竞争车型选择原则选择好竞争车型后,列出各个竞争车型的长x1、宽x2、高x3、投影面积(整车俯视图投影到地面的面积)x4,单位面积质量(整车质量与长×宽的比值)x5、体积(长×宽×高)x6、密度(整车质量与体积的比值)x7、油耗x8、制动距离x9等与整车质量关联度较高的影响因素,建立相关的案例数据库,供使用时调取参考。

设一阶矩阵为X=[x1x2x3x4x5x6x7x8x9],则整车质量Y可表示为Y=aXT+a0,其中a为一阶矩阵，a=[a1a2a3a4a5a6a7a8a9],a0为常数。a和a0可根据相关数据,运用多元回归法进行计算后确定。本文利用Excel内部函数LINEST函数进行多元回归分析[10]。

用9个变量进行多元回归分析,实际操作比较困难,而且很多变量和质量之间影响关系可能很弱,因此需要分析每个变量与整车质量相关性的强弱,剔除不重要的变量,在不太影响分析结果的情况下简化计算。

每个变量xi与整车质量y之间的关系用一元回归法进行分析[11-12],可以得到如下关系:

(2)

(3)

R2=C为相关性指数,表达变量xi与整车质量y之间的相关性。C的值越大,变量xi与整车质量y之间的相关性就越强。通过相关性指数可确定整车质量的关键变量。

针对有关车型的数据,经过详细的大量计算发现,单位面积质量对整车的质量影响最大。例如,经回归分析,整车质量与单位面积质量之间的关系为y=lwx5-1.957(见后文算例),其中,l为车型的长,w为车型的宽。将该公式用于所挑选的3款车型整车质量计算。分析案例见表1所列。

表1　3款车型案例数据

采用多元回归分析得到车型A、B、C的质量分别为1 268.78、1 259、1 358.4kg,而采用一元回归公式y=lwx5-1.957得到的质量分别为1 267.05 、1 258、1 360.0kg。从这3款车型的计算来看,一元回归法的结果和多元回归法的结果相差很小,在误差允许的范围内,因此可以将单位面积质量作为确定整车质量的关键变量。

确定整车质量的关键变量后,只要知道变量xi的参数值,就可以根据(2)式计算出目标车型的质量。随着轻量化技术的发展,市场上有竞争力的整车质量呈逐年下降的趋势,而一般开发的目标车型需要经过3~4a的开发验证后才能上市,这就不可避免为开发带来一定的盲目性和未确知性。因此,为了保障目标车型具有质量轻的优势,在制定目标时就需要考虑、预测未来几年整车质量下降的趋势,对整车质量设定目标控制。整车质量目标设定是以年份表示质量的变化情况,若通过(2)式已找出影响整车质量的关键变量xi,则根据以往的数据,采用一元回归分析法,找出关键变量xi与车辆上市年份的关系,即可对整车质量进行预测。

设通过一元回归分析,得出关键变量xi与车辆上市年份z之间的关系为:

(4)

将(4)式代入(2)式,可得到计算整车质量目标与车辆上市年份之间的公式为:

(5)

不论运用多元回归分析,还是运用一元回归法,最终得到的整车质量目标计算公式的相关性参数都是根据竞争车型的质量数据库分析得出的,所以这个数据库所涵盖的车型越多,预测的结果就越准确。

3整车质量目标的分解

设定了整车级的质量目标,可根据类比法,分解系统级的质量目标。本文主要采用2种方式进行整车质量目标的分解。

(1) 白车身系统质量目标的分解。对于白车身,行业通用的是引入轻量化系数。轻量化系数可用(6)式表述：

(6)

其中,L为轻量化系数;mBIW为白车身质量;CT为白车身扭转刚度;A为车辆轮距与轴距的投影面积。

轻量化系数反映的是白车身轻量化设计的水平,系数越低表示白车身轻量化水平越高,国外先进车型的轻量化系数都在4.0以下,而国内自主品牌的轻量化系数普遍偏高。

白车身的轻量化系数也反映了一个公司的产品开发能力和制造能力水平,随着技术的发展,它是一个动态调整的过程。在设定一个新开发车型的轻量化系数目标时同样参考同级别的其他市场竞争车型的参数[2],一般可取竞争车型轻量化系数的平均值3.9,根据新开发车型的车身扭转刚度目标、车型尺寸来设定白车身的质量目标。

(2) 整车其他系统目标的分解与制定。各系统的质量目标分解与制定采取比值法来进行。比值法是指该系统在整车质量中所占的比重。竞争车型的每个系统的质量相对于整车质量的比重,每个系统、每个车型都有一个各个系统比重的分析值,在设定新车型的各系统目标时,根据每个系统比重的平均值乘以整车目标质量就得到了各个系统的目标质量。这里需要注意的是,车身系统含白车身和车身附件2部分,对于白车身的目标设定在前面已经进行了分析,根据比重所确定的车身系统的质量减去白车身的质量就是车身附件的质量目标。

4应用示例

对已往多种车型,调取数据库中的数据,得到竞争车型的主要数据见表2所列。

根据表2的数据进行一元回归分析,结果见表3所列。由表3可知,单位面积质量与整车质量的相关性指数R2=0.706,说明单位面积质量对整车的质量影响最大。整车高度、油耗和制动性与整车质量的相关性指数分别为R2=0.008、R2=0.006和R2=0.042,说明这几个因素对整车质量的影响不大,可以不予考虑。体积对整车质量的影响也不大,因为体积虽然含有面积参数,但也含有与整车的质量关系不大的高度参数。密度对整车质量的影响比体积对整车质量的影响稍大,因为密度不仅含有体积信息,还含有质量信息。显然,单位面积质量这个变量也涵盖了整车长、宽、投影面积、质量等信息,且抛开了与整车质量关系不大的高度信息,所以最终确定采用单位面积质量作为整车质量的关键变量参数。

根据表3可知,以单位面积质量为关键变量参数的回归结果y=8 091 000x5-1.957,其中的8 091 000是一元回归的统计均值,在计算具体车型时,可以用整车长l和宽w的乘积代替。因此,y对关键参数x5的一元回归可表示为：

y=lwx5-1.957。

图1所示为单位面积质量与车型年份的关系。

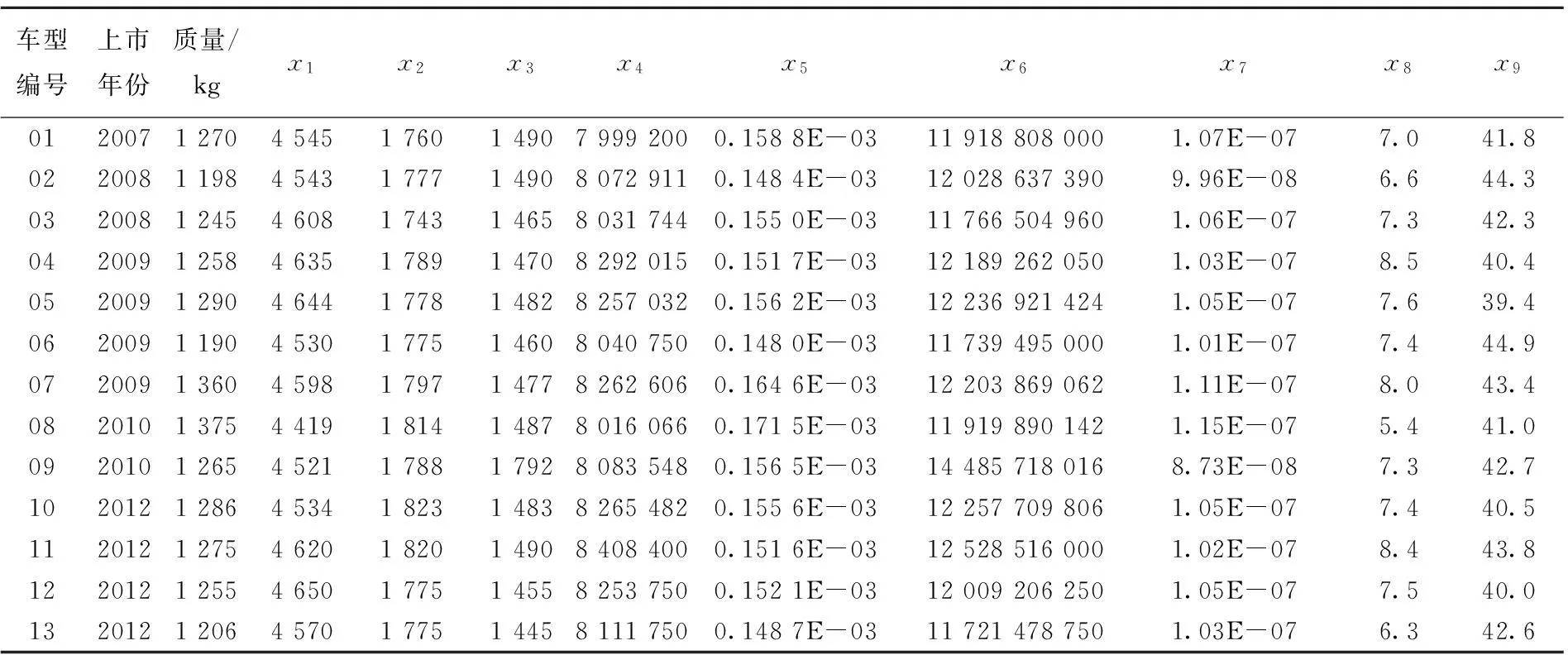
表2　竞争车型主要数据

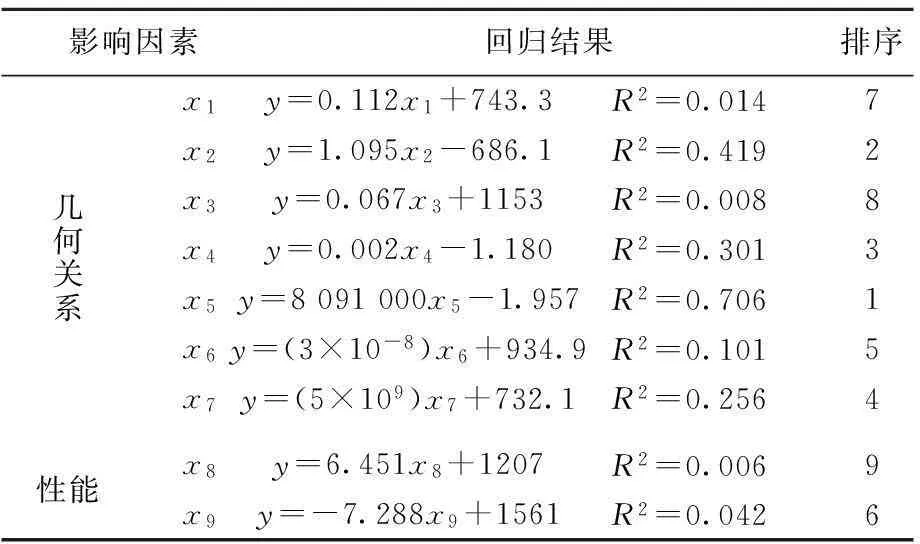
表3　一元回归分析结果

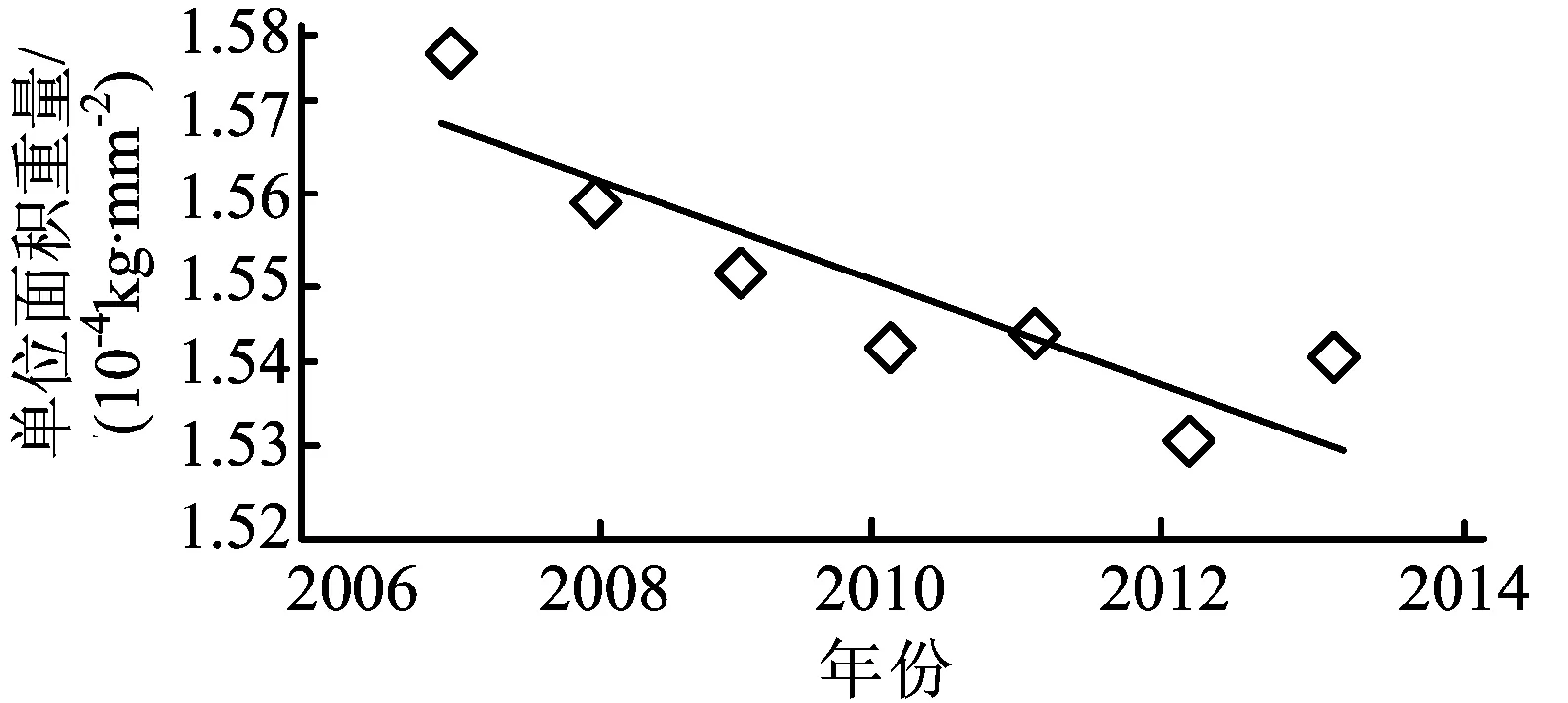
图1　单位面积质量与车型年份的关系

采用一元回归分析,得单位面积质量xi与车辆上市年份z之间的关系为：

因此可得,整车质量目标与车辆上市年份之间的公式为：

(1.4×10-3)lw-1.957。

目标车型长l为4 650 mm,宽w为1 820 mm,计划2015年上市,则该车型的整车质量目标为：

y=(-6.19×10-7)×4 650×1 820×2 015+

(1.4×10-3)×4 650×1 820-1.957=

1 290 kg。

整车系统质量目标的分解见表4所列。

表4　整车质量分解

5结束语

整车质量目标的制定与分解在行业内的研究不是很多,更多的是集中在轻量化技术的应用上。本文结合竞争车型质量数据库分析,将统计学中的二元回归法和一元回归法运用到整车质量目标设定过程中,研究出了整车质量目标设定的相关公式。同时分析各个系统的质量在整车质量中所占的比重,通过比值法来完成整车质量目标的分解过程。本文所有的研究参数基于数据库,数据库越强大,本文所研究的整车质量目标制定和分解方法的准确性越高。

[参考文献]

[1]王智文.汽车轻量化技术发展现状初探[J].汽车工艺与材料,2009(2):2-3.

[2]魏元生.长城汽车轻量化技术的应用研究[J].汽车工艺与材料,2011(1):18-19.

[3]高新华,王昱昕，李中兵.汽车轻量化技术在奇瑞轿车上的集成应用[J].汽车工艺与材料,2011(1):11-23.

[4]吕红萍.轿车车身的轻量化设计[J].汽车与配件，2011(5):42-44.

[5]张国胜,周超,崔海涛.轿车车身结构轻量化[J].公路交通科技,2012(1):154-158.

[6]向晓峰,魏丽霞,马鸣图,等.汽车轻量化技术的应用[J].汽车工程师,2012(5):57-59.

[7]陈玉莲.汽车车身轻量化的研究进展[J].热加工工艺,2012,14(5):24-29.

[8]何昌德,杨普新.轻量化材料及加工技术在现代汽车上的发展和应用[J].装备制造技术,2011(2):93-96.

[9]王志亮,门永新，彭鸿，等.基于模态和刚度的白车身优化分析[J].机械科学与技术,2008(8):1021-1024.

[10]褚永康,文桂林，崔中，等. 基于遗传算法的汽车变速箱轻量化设计[J].合肥工业大学学报：自然科学版,2011,34(10):1461-1465.

[11]周自玮.利用Excel内部函数LINEST进行多元回归和多项式回归分析[J].草业与蓄牧,2007(8):48-52.

[12]董文鹏. 基于Excel的一元回归分析[J].河北水利,2011,(6)：36.

(责任编辑马国锋)

Research on vehicle weight goal setting and decomposition

GAO Xin-hua1,2，TU Shao-ping2，WANG Qi-dong1

(1.School of Machinery and Automobile Engineering, Hefei University of Technology, Hefei 230009, China; 2.Vehicle Engineering Center, Chery Automobile Co., Ltd., Wuhu 241009, China)

Abstract:The method of vehicle weight goal setting and decomposition is studied. The main parameter relevant to the vehicle weight is found out by comparing the results obtained by using multivariate regression analysis and simple regression analysis. The formula of the relationship between the main parameter and the vehicle weight is gotten based on simple regression analysis. Therefore, the vehicle weight target can be determined, and the weight is decomposed by using ratio analysis method.

Key words:weight goal; multivariate regression method; simple regression method; ratio analysis method

中图分类号:TG142. 1; TG81

文献标识码：A

文章编号：1003-5060(2016)02-0166-05

Doi:10.3969/j.issn.1003-5060.2016.02.005

作者简介：高新华(1971-),男,安徽芜湖人,合肥工业大学博士生,奇瑞汽车有限公司正高级工程师；王其东(1964-),男,安徽阜南人,博士,合肥工业大学教授,博士生导师.

收稿日期：2014-12-29；修回日期：2015-01-19